苏教版六年级下学期数学7.2图形与几何课件(共21张PPT)
文档属性
| 名称 | 苏教版六年级下学期数学7.2图形与几何课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 29.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 13:30:19 | ||
图片预览




文档简介
(共21张PPT)
图形与几何
1.方向
2.方位
3.确定位置
4.线路图
图形与位置
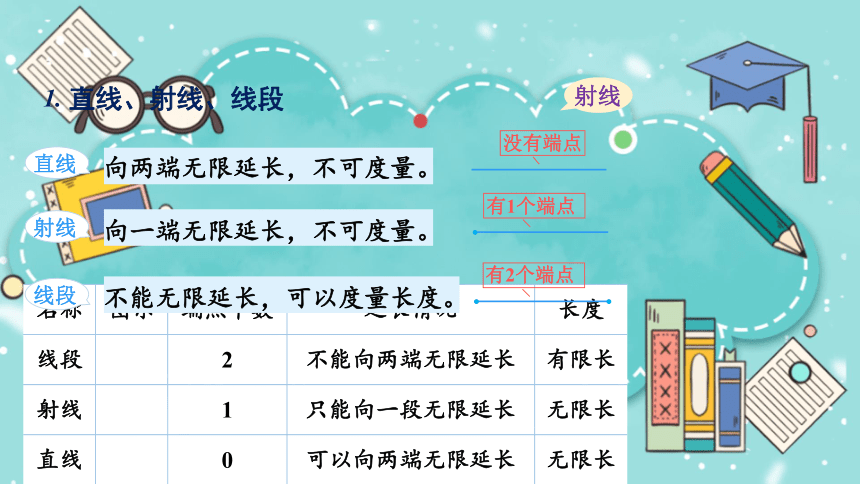
直线、射线、线段
1.
名称 图示 端点个数 延长情况 长度
线段 2 不能向两端无限延长 有限长
射线 1 只能向一段无限延长 无限长
直线 0 可以向两端无限延长 无限长
向两端无限延长,不可度量。
直线
射线
向一端无限延长,不可度量。
不能无限延长,可以度量长度。
射线
线段
没有端点
有1个端点
有2个端点
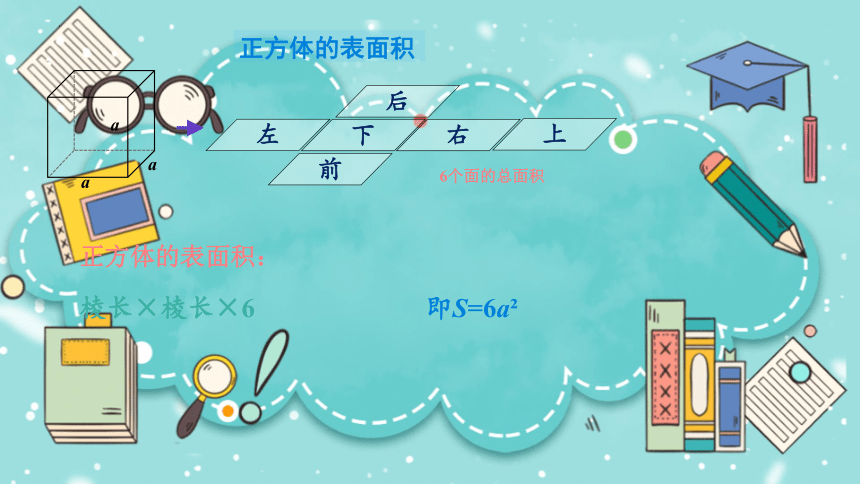
正方体的表面积:
棱长×棱长×6
a
a
a
后
前
左
右
上
下
即S=6a
正方体的表面积
6个面的总面积
思考(二)
回顾整理
什么是轴对称图形?什么是对称轴?在我们学过的几何图形中,有哪些是轴对称图形?
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴。
正方形、长方形、等腰三角形、等腰梯形和圆都是轴对称图形,有的轴对称图形不止一条对称轴。
顶点
底面
O
r
h
高
①有一个顶点。
②有一个底面,是个圆形。
③有一个侧面,是个曲面,
展开是个扇形。
④有一条高。
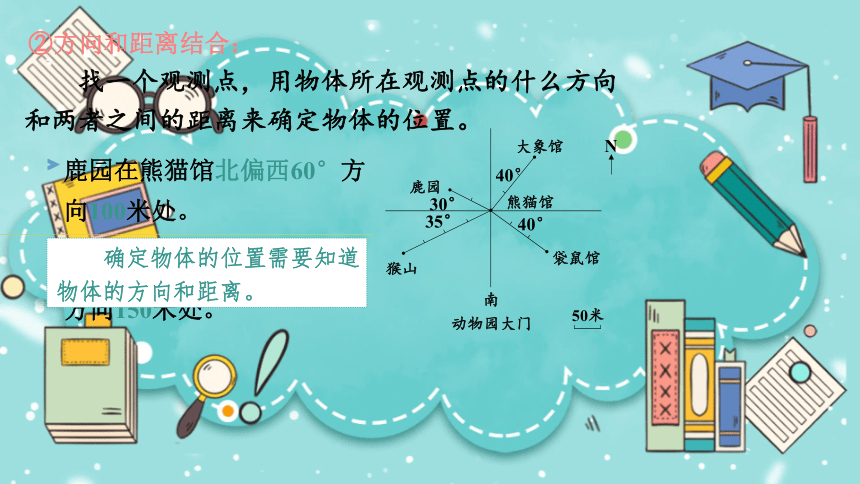
②方向和距离结合:
找一个观测点,用物体所在观测点的什么方向和两者之间的距离来确定物体的位置。
大象馆
熊猫馆
猴山
N
50米
鹿园
南
动物园大门
40°
40°
30°
35°
袋鼠馆
鹿园在熊猫馆北偏西60°方向100米处。
袋鼠馆在熊猫馆南偏东50°方向150米处。
确定物体的位置需要知道物体的方向和距离。
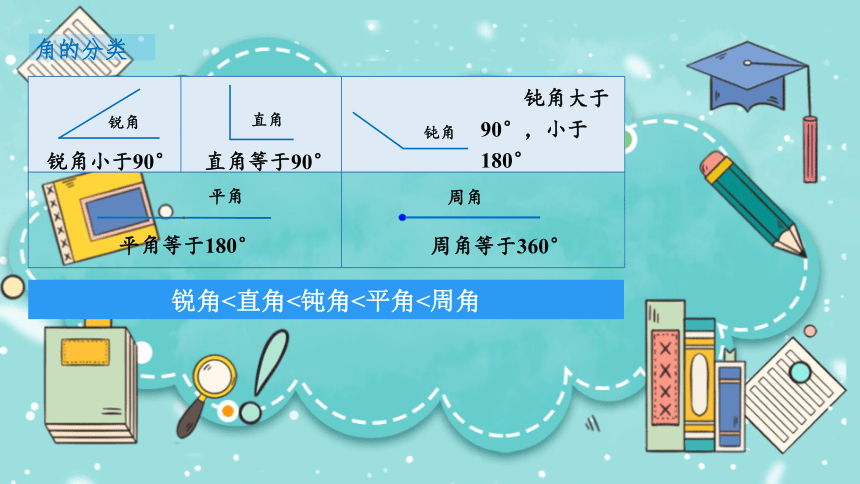
角的分类
锐角小于90°
直角等于90°
钝角大于90°,小于180°
锐角
直角
钝角
平角等于180°
周角等于360°
平角
周角
1平角=2直角
1周角=2平角=4直角
锐角<直角<钝角<平角<周角
a
h
b
长方体的体积 = 长 × 宽 × 高
V=abh
长方体
正方体
正方体的体积
棱长
棱长
×
=
×
棱长
a
a
a
V=a
表示三个a相乘。
把图 B 向右平移 5 格,再向上平移 3 格。
以电视塔为观测点,填一填,画一画。
(1)市民广场在电视塔( )方向( )米处,
电信大楼在电视塔( )方向( )米处。
正东
160
正北
240
从下面的长方形纸上剪下一部分,折成一个棱长
2厘米的正方体,可以怎样剪?设计两种不同的
方案,在图中涂色表示。
答案不唯一。
圆和扇形
直径d
半径r
圆心O
圆是由曲线围成的,圆上任意一点到圆心的距离都相等。
一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形,扇形是圆的一部分。
扇形
所有的半径都相等,所有的直径也相等。
把左边的圆平移,使平移后的圆与右边的线段组成轴对称图形。
(1)圆应向什么方向平移几格?
(2)你能画出组成的轴对称图形的
对称轴吗?
(3)对称轴通过圆心吗?它与已知
线段有什么关系?
答:圆应向右平移5格。
O
动手操作
互相垂直
计算下面立体图形的表面积和体积。
①表面积:4 ×6=96(平方厘米)
体积:4×4×4=64(立方厘米)
①
②
③
②表面积:(5×3+4×3+5×4)=94(平方厘米)
体积:5×4×3=60(立方厘米)
③表面积:3.14×10×5=157(平方厘米)
3.14×(10÷2) ×2=157(平方厘米)
157+157=314(平方厘米)
体积:3.14×(10÷2) ×5=392.5(立方厘米)
先估计下面每个角的度数,再用量角器量一量。
估计( )°
测量( )°
估计( )°
测量( )°
估计( )°
测量( )°
50
150
90
50
150
90
7. 制作下面的圆柱形物体,至少各需要多少铁皮?
油桶:
3.14×4 ×2+3.14×4×2×12=401.92(平方分米)
水桶:
3.14×(40÷2) +3.14×40×50=7536(平方厘米)
通风管:0.628×1.2=0.7536(平方米)
用6个同样大的正方体摆成的物体,从
前面看到的形状如右图。摆一摆,并分
别从右面和上面看一看,各是什么形状?
答案不唯一。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
感谢同学们积极配合!
图形与几何
1.方向
2.方位
3.确定位置
4.线路图
图形与位置
直线、射线、线段
1.
名称 图示 端点个数 延长情况 长度
线段 2 不能向两端无限延长 有限长
射线 1 只能向一段无限延长 无限长
直线 0 可以向两端无限延长 无限长
向两端无限延长,不可度量。
直线
射线
向一端无限延长,不可度量。
不能无限延长,可以度量长度。
射线
线段
没有端点
有1个端点
有2个端点
正方体的表面积:
棱长×棱长×6
a
a
a
后
前
左
右
上
下
即S=6a
正方体的表面积
6个面的总面积
思考(二)
回顾整理
什么是轴对称图形?什么是对称轴?在我们学过的几何图形中,有哪些是轴对称图形?
如果一个图形沿着一条直线对折,两侧的图形能够完全重合,这个图形就是轴对称图形。折痕所在的这条直线叫做对称轴。
正方形、长方形、等腰三角形、等腰梯形和圆都是轴对称图形,有的轴对称图形不止一条对称轴。
顶点
底面
O
r
h
高
①有一个顶点。
②有一个底面,是个圆形。
③有一个侧面,是个曲面,
展开是个扇形。
④有一条高。
②方向和距离结合:
找一个观测点,用物体所在观测点的什么方向和两者之间的距离来确定物体的位置。
大象馆
熊猫馆
猴山
N
50米
鹿园
南
动物园大门
40°
40°
30°
35°
袋鼠馆
鹿园在熊猫馆北偏西60°方向100米处。
袋鼠馆在熊猫馆南偏东50°方向150米处。
确定物体的位置需要知道物体的方向和距离。
角的分类
锐角小于90°
直角等于90°
钝角大于90°,小于180°
锐角
直角
钝角
平角等于180°
周角等于360°
平角
周角
1平角=2直角
1周角=2平角=4直角
锐角<直角<钝角<平角<周角
a
h
b
长方体的体积 = 长 × 宽 × 高
V=abh
长方体
正方体
正方体的体积
棱长
棱长
×
=
×
棱长
a
a
a
V=a
表示三个a相乘。
把图 B 向右平移 5 格,再向上平移 3 格。
以电视塔为观测点,填一填,画一画。
(1)市民广场在电视塔( )方向( )米处,
电信大楼在电视塔( )方向( )米处。
正东
160
正北
240
从下面的长方形纸上剪下一部分,折成一个棱长
2厘米的正方体,可以怎样剪?设计两种不同的
方案,在图中涂色表示。
答案不唯一。
圆和扇形
直径d
半径r
圆心O
圆是由曲线围成的,圆上任意一点到圆心的距离都相等。
一条弧和经过这条弧两端的两条半径所围成的图形叫作扇形,扇形是圆的一部分。
扇形
所有的半径都相等,所有的直径也相等。
把左边的圆平移,使平移后的圆与右边的线段组成轴对称图形。
(1)圆应向什么方向平移几格?
(2)你能画出组成的轴对称图形的
对称轴吗?
(3)对称轴通过圆心吗?它与已知
线段有什么关系?
答:圆应向右平移5格。
O
动手操作
互相垂直
计算下面立体图形的表面积和体积。
①表面积:4 ×6=96(平方厘米)
体积:4×4×4=64(立方厘米)
①
②
③
②表面积:(5×3+4×3+5×4)=94(平方厘米)
体积:5×4×3=60(立方厘米)
③表面积:3.14×10×5=157(平方厘米)
3.14×(10÷2) ×2=157(平方厘米)
157+157=314(平方厘米)
体积:3.14×(10÷2) ×5=392.5(立方厘米)
先估计下面每个角的度数,再用量角器量一量。
估计( )°
测量( )°
估计( )°
测量( )°
估计( )°
测量( )°
50
150
90
50
150
90
7. 制作下面的圆柱形物体,至少各需要多少铁皮?
油桶:
3.14×4 ×2+3.14×4×2×12=401.92(平方分米)
水桶:
3.14×(40÷2) +3.14×40×50=7536(平方厘米)
通风管:0.628×1.2=0.7536(平方米)
用6个同样大的正方体摆成的物体,从
前面看到的形状如右图。摆一摆,并分
别从右面和上面看一看,各是什么形状?
答案不唯一。
课后作业
1.从课后习题中选取;
2.完成练习册本课时的习题。
感谢同学们积极配合!
