北师大版四年级下册数学单元测试卷-第5单元认识方程数学好玩(含答案)
文档属性
| 名称 | 北师大版四年级下册数学单元测试卷-第5单元认识方程数学好玩(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 62.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 14:02:54 | ||
图片预览




文档简介
第5单元 认识方程+数学好玩
一.选择题
1.五年级种树60棵,比四年级种的2倍少4棵。四年级种树多少棵?设四年级种树x棵,下列方程错误的是( )。
A.2x=60﹣4 B.2x﹣4=60 C.2x=60+4 D.60+4=2x
2.下面各组式子中,不一定相等的是( )
A.4a和a+a+a+a B.a2和a+a
C.a2和a×a
3.如图,天平平衡了,下列数量关系正确的是( )
A.3m=2n B.m=2n C.n=2m
4.方程一词,最早出现在我国古代数学书籍《九章算术》中。下列式子是方程的是( )
A.3x+2y B.5x÷6>3 C.5×3=15 D.a﹣2=7
5.已知3x+2=11,那么4x﹣1=( )
A.9 B.13 C.11
6.五年级植树120棵,比三年级植树棵数的3倍多6棵,三年级植树多少棵?设三年级植树x棵,下列方法错误是( )
A.3x+6=120 B.3x﹣6=120 C.120﹣3x=6 D.3x=120﹣6
7.在下面给出的平面图形中,不能进行密铺的是( )
A.三角形 B.四边形 C.正七边形
8.学校组织体检,三位小朋友量得的身高如下,身高最高的是( )
A.1.24米 B.1.4米 C.1.54米
二.填空题
9.故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。设天安门广场的面积是x万平方米,根据题意写出一个等量关系式:
,根据这个等量关系式写出相应的方程 。
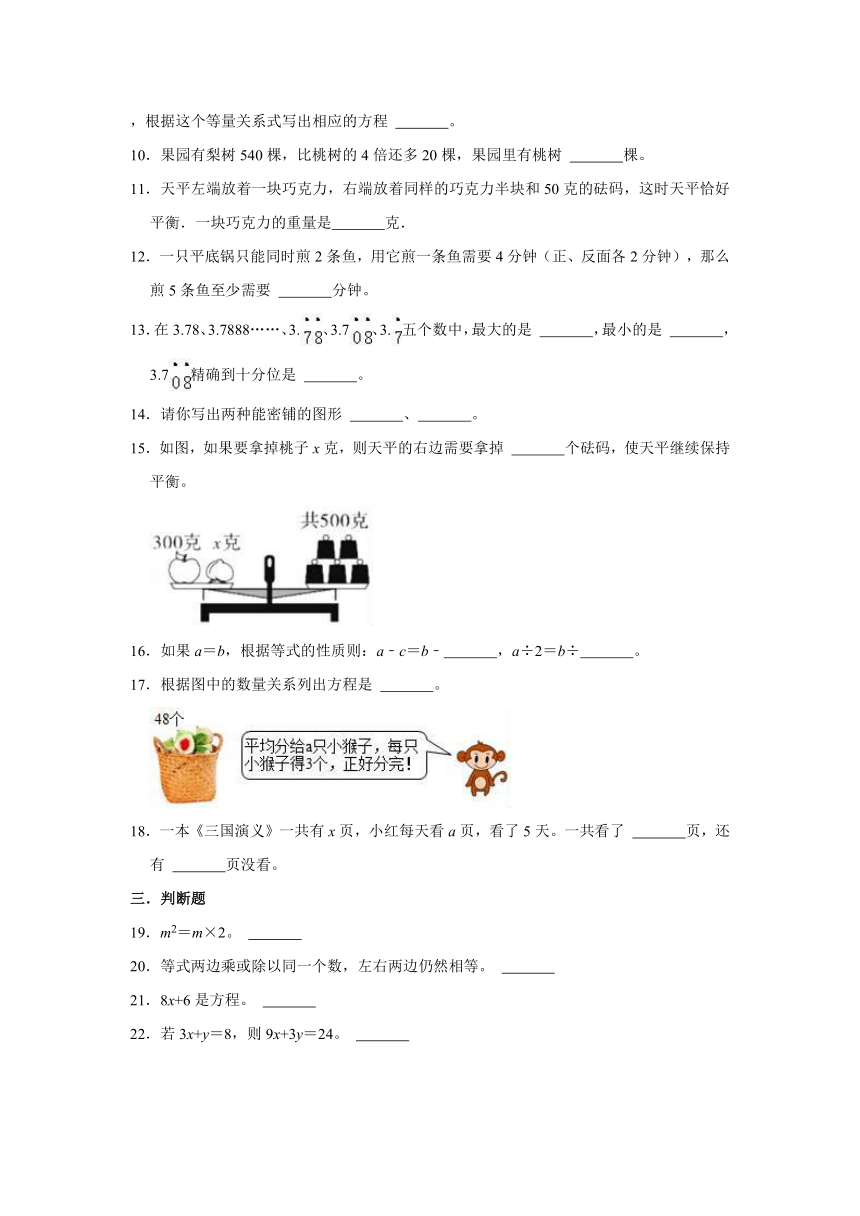
10.果园有梨树540棵,比桃树的4倍还多20棵,果园里有桃树 棵。
11.天平左端放着一块巧克力,右端放着同样的巧克力半块和50克的砝码,这时天平恰好平衡.一块巧克力的重量是 克.
12.一只平底锅只能同时煎2条鱼,用它煎一条鱼需要4分钟(正、反面各2分钟),那么煎5条鱼至少需要 分钟。
13.在3.78、3.7888……、3.、3.7、3.五个数中,最大的是 ,最小的是 ,3.7精确到十分位是 。
14.请你写出两种能密铺的图形 、 。
15.如图,如果要拿掉桃子x克,则天平的右边需要拿掉 个砝码,使天平继续保持平衡。
16.如果a=b,根据等式的性质则:a﹣c=b﹣ ,a÷2=b÷ 。
17.根据图中的数量关系列出方程是 。
18.一本《三国演义》一共有x页,小红每天看a页,看了5天。一共看了 页,还有 页没看。
三.判断题
19.m2=m×2。
20.等式两边乘或除以同一个数,左右两边仍然相等。
21.8x+6是方程。
22.若3x+y=8,则9x+3y=24。
23.小明家的平底锅一次能同时烙2张饼,烙一张饼需要6分钟(正反面各3分钟),小明用27分钟的时间最多可以烙8张饼。
四.计算题
24.求铅笔和钢笔本各有多少支?
25.解方程。
x÷8=0.4 5x+28=48 3x﹣4×6=48
五.应用题
26.森林公园的面积是61公顷,比青年广场面积的4倍多9公顷,青年广场的面积是多少公顷?(用方程解)
27.学校组织五、六年级同学听抗疫英雄巡回演讲会,一共有972人。报告厅每排可以坐18人,五年级坐了26排,六年级坐了多少排?(列方程解答)
28.若方程2x+3=21与5x﹣m=30的解相同,则m是多少?
29.小芳看一本300页的故事书,她每天看x页,已经看了7天,先用式子表示这本书还剩多少页没看?再计算当x=25时,还剩多少页没看?
30.妈妈回家做饭,淘米要3分钟,煮饭要30分钟,洗菜要8分钟,切菜要5分钟,炒菜要10分钟。如果煮饭和炒菜要用不同的锅和炉子,妈妈要将饭菜都做好,最少要用多长时间,说明你的想法。
31.在60米短跑比赛中,前三名当中李红的成绩是9.1秒,刘英的成绩是9.4秒,王丽的成绩是8.9秒.请你把她们比赛的名次排出来.
32.电饼铛里每次能同时放2个烧饼,如果烧熟1个烧饼的正反两面各需要2分,那么烤熟5个烧饼至少需要多少分?
参考答案
一.选择题
1.【分析】四年级种树的棵树×2﹣4=五年级种树的棵树,据此等量关系列出方程即可。
【解答】解:2x﹣4=60
2x﹣4+4=60+4
2x=64
2x÷2=64÷2
x=32
答:四年级种树32棵。
故选:A。
【点评】根据题意找出等量关系,列出方程即可解决此题。
2.【分析】4a=4×a=a+a+a+a,A项两个式子一定相等;a2=a×a,C项两个式子一定相等,B项两个式子不一定相等。
【解答】解:不一定相等的是a2和a+a。
故选:B。
【点评】此题的关键是明确带字母式子的意义,然后再进一步解答。
3.【分析】天平平衡了,说明两边的总量相等。也就是m+m+m=m+n,两边同时减去m可得2m=n,据此解答。
【解答】解:m+m+m=m+n
m+m+m﹣m=m+n﹣m
2m=n
数量关系正确的是n=2m。
故选:C。
【点评】此题的关键是明确天平平衡时两边总量相等,然后再进一步解答。
4.【分析】方程是指含有未知数的等式;所以方程必须具备两个条件:①含有未知数;②等式。据此解答。
【解答】解:3x+2y、5x÷6>3不是等式;
5×3=15不含有未知数;
a﹣2=7含有未知数,是等式,是方程。
故选:D。
【点评】此题考查方程的辨识:只有含有未知数的等式才是方程。
5.【分析】根据等式的性质,先求出方程3x+2=11的解,然后再代入4x﹣1求出值即可。
【解答】解:3x+2=11
3x+2﹣2=11﹣2
3x=9
3x÷3=9÷3
x=3
把x=3代入4x﹣1可得:
4×3﹣1=11。
故选:C。
【点评】本题关键是根据等式的性质求出方程的解,然后再代入含有未知数的式子求出值。
6.【分析】这道题的等量关系非常明显,三年级植树的棵数×3+6棵=五年级植树的棵数120,由此设出三年级植树x棵,列出方程解答即可。
【解答】解:A.根据三年级植树的棵数×3+6棵=五年级植树的棵数120,可得3x+6=120,本项不符合题意;
B.3x﹣6=120错误,本项符合题意;
C.根据五年级植树的棵数120﹣三年级植树的棵数×3=6棵,可得120﹣3x=6,本项不符合题意;
D.根据三年级植树的棵数×3=五年级植树的棵数(120﹣6)棵,可得3x=120﹣6,本项不符合题意。
故选:B。
【点评】解决这类问题主要找出题里面蕴含的数量关系,由此列出方程解决问题。
7.【分析】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角;360°为正多边形一个内角的整数倍才能单独镶嵌。
【解答】解:在上面给出的平面图形中,不能进行密铺的是正七边形,三角形和四边形能进行密铺。
故选:C。
【点评】本题考查了平面镶嵌(密铺),用一种正多边形镶嵌,只有三角形、四边形、六边形三种正多边形能镶嵌成一个平面图案。
8.【分析】比较小数的大小时,要先比较整数部分的位数,它们的数位如果不同,那么数位多的那个数就大,如果数位相同,相同数位上的数大的那个数就大;如果整数部分相同,然后再比较小数部分的十分位、百分位、千分位……;据此解答即可。
【解答】解:1.24<1.4<1.54
所以身高最高的是1.54米。
故选:C。
【点评】此题考查了小数大小比较方法的灵活运用。
二.填空题
9.【分析】由题意可以得到数量关系:天安门广场的面积×2﹣16=故宫的面积,设出天安门广场的面积,依据得到的等量关系,即可列出符合题意的方程。
【解答】解:设天安门广场的面积是x万平方米,天安门广场的面积×2﹣16=故宫的面积,
2x﹣16=72
2x=88
x=44
故答案为:天安门广场的面积×2﹣16=故宫的面积,2x﹣16=72。
【点评】解答此题的关键是:依据题意,把一倍的量设为未知数,然后找出等量关系,即可列出方程。
10.【分析】设桃树有x棵,依据题意桃树棵数×4+20棵=梨树棵数可列方程:4x+20=540,依据等式的性质即可求解。
【解答】解:设桃树有x棵
4x+20=540
4x+20﹣20=540﹣20
4x÷4=520÷4
x=130
答:果园里有桃树130棵。
故答案为:130。
【点评】解答本题的关键是依据题意列出方程,解答依据是等式的性质。
11.【分析】根据题意得出一块巧克力的重量=半块巧克力的重量+50,由此得出半块巧克力的重量,进而求出一块巧克力的重量.
【解答】解:根据题意得出半块巧克力的重量是50克,
所以1块巧克力的重量为:50×2=100(克),
答:一块巧克力的重量是100克;
故答案为:100.
【点评】关键是根据题意求出半块巧克力的重量是50克,进而解决问题.
12.【分析】烙饼问题公式:总时间=饼数×2÷每锅的可烙的数量×烙每面的时间。把XX看作饼,代入公式计算即可。
【解答】解:5×2÷2×2
=5×2
=10(分钟)
答:煎5条鱼至少需要10分钟。
故答案为:10。
【点评】此题考查了烙饼问题的应用,要熟记公式。
13.【分析】根据小数大小比较的方法:比较两个小数的大小,先看它们的整数部分,整数部分大的那个数就大,整数部分相同的,十分位上的数大的那个数就大,十分位上的数也相同的,百分位上的数大的那个数就大直接比较可得;精确到十分位就要看小数点后面第二位,再根据“四舍五入“法取近似数即可。
【解答】解:因为3.7888……>3.>3.78>3.>3.7
所以在3.78、3.7888……、3.、3.7、3.五个数中,最大的是3.7888…,最小的是3.7;
3.7≈3.7
所以3.7精确到十分位是 3.7。
故答案为:3.7888……,3.7,3.7。
【点评】此题主要考查了小数比较大小的方法的应用以及根据“四舍五入”
法求近似数,要熟练掌握。
14.【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠; (3)连续铺成一片。能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合。圆、半圆、正五边形就不具备这样的特点。
【解答】解:两种能密铺的图形是正方形和正六边形。
故答案为:正方形和正六边形。(答案不唯一)
【点评】考查了平面镶嵌(密铺)问题,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角。
15.【分析】天平平衡则有300+x=500,再根据等式的基本性质可求得x的质量,右边5个砝码是500克,据此可算出一个砝码是100克,据此解答即可。
【解答】解:300+x=500
300+x﹣300=500﹣300
x=200
500÷5=100(克)
200÷100=2(个)
【点评】熟练掌握等式的基本性质是解题的关键。
16.【分析】等式的基本性质1:等式两边同时加上(或减去)同一个数,等式仍然成立;
等式的基本性质2:等式两边同时乘(或除以)同一个不为0的数,等式仍然成立,据此计算即可。
【解答】解:a=b
a﹣c=b﹣c
a=b
a÷2=b÷2
【点评】熟练掌握等式的基本性质是解题的关键。
17.【分析】每只小猴子分到的个数×小猴子的只数=桃子总数,据此列方程即可。
【解答】解:根据图中的数量关系列出方程是3a=48。
故答案为:3a=48。
【点评】列方程解应用题,关键是根据题意找出基本数量关系,正确列出方程。
18.【分析】每天看a页,看了5天,则一共看了(5×a)页,用总页数减去看了的页数就是没看的页数。
【解答】解:一共看了5a页,还有(x﹣5a)页没看。
故答案为:5a,(x﹣5a)。
【点评】此题的关键是先求出看了的页数,然后再进一步解答。
三.判断题
19.【分析】m2=m×m,据此判断即可。
【解答】解:m2=m×m,
故原题说法错误。
故答案为:×。
【点评】此题主要考查了平方的意义,要熟练掌握。
20.【分析】等式两边同时乘或除以同一个不为0的数,等式仍然成立。
【解答】解:题干没有强调除以不为0的数。
故原题说法错误。
故答案为:×。
【点评】此题考查了等式的性质,要熟练掌握。
21.【分析】方程是指含有未知数的等式;所以方程必须具备两个条件:①含有未知数;②等式。据此解答。
【解答】解:8x+6不是等式,因此不是方程。
故原题说法错误。
故答案为:×。
【点评】此题考查方程的辨识:只有含有未知数的等式才是方程。
22.【分析】等式两边同时加上(或减去)同一个数,等式仍然成立。等式两边同时乘或除以同一个不为0的数,等式仍然成立。
【解答】解:若3x+y=8,则等式两边同时乘3,可以得到9x+3y=24。
故原题说法正确。
故答案为:√。
【点评】此题考查了等式的性质,要熟练掌握。
23.【分析】烙饼问题公式:总时间=饼数×2÷每锅的可烙的数量×
烙每面的时间,代入公式计算并比较即可。
【解答】解:8×2÷2×3
=8×3
=24(分钟)
24<27
9×2÷2×3
=9×3
=27(分钟)
小明用27分钟的时间最多可以烙9张饼。
故原题说法错误。
故答案为:×。
【点评】此题考查了烙饼问题的应用,要熟记公式。
四.计算题
24.【分析】根据题意,设铅笔有x支,则钢笔为(2x﹣2)支,有关系式:铅笔支数+钢笔支数=10支,列方程求解即可求出铅笔支数,再求钢笔即可.
【解答】解:设铅笔有x'支,
x+2x﹣2=10
3x=12
x=4
4×2﹣2
=8﹣2
=6(支)
答:铅笔有4支,钢笔有6支.
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题.
25.【分析】(1)根据等式的基本性质,方程两边同时乘8即可;
(2)根据等式的基本性质,方程两边同时减去28,两边再同时除以5;
(3)根据等式的基本性质,方程两边同时加上24,两边再同时除以3。
【解答】解:(1)x÷8=0.4
x÷8×8=0.4×8
x=3.2
(2)5x+28=48
5x+28﹣28=48﹣28
5x=20
5x÷5=20÷5
x=4
(3)3x﹣4×6=48
3x﹣4×6+24=48+24
3x=72
3x÷3=72÷3
x=24
【点评】熟练掌握等式的基本性质是解题的关键。
五.应用题
26.【分析】设青年广场的面积是x公顷,根据等量关系:青年广场面积×4+9公顷=森林公园的面积,列方程解答即可。
【解答】解:设青年广场的面积是x公顷,
4x+9=61
4x=52
x=13
答:青年广场的面积是13公顷。
【点评】本题考查了列方程解应用题,关键是根据等量关系:青年广场面积×4+9公顷=森林公园的面积列方程。
27.【分析】根据题意,设六年级坐了x排;根据题意可得:(五年级坐的排数+六年级坐的排数)×每排坐的人数=总人数,据此列出方程进行解答。
【解答】解:设六年级坐了x排,根据题意可得:
(26+x)×18=972
(26+x)×18÷18=972÷18
26+x=54
26+x﹣26=54﹣26
x=28
答:六年级坐了28排。
【点评】列方程解决实际问题,关健是根据题意设出未知数,找出等量关系,然后再列出方程进行解答。
28.【分析】方程2x+3=21,根据等式的性质,方程两边同时减去3,再两边同时除以2,求出x的值;再把x的值代入5x﹣m=30求出m是多少即可.
【解答】解:2x+3=21
2x+3﹣3=21﹣3
2x=18
2x÷2=18÷2
x=9
把x=9代入5x﹣m=30
5×9﹣m=30
45﹣m=30
45﹣m+m=30+m
45=30+m
45﹣30=30+m﹣30
m=15
答:m是15.
【点评】此题考查了根据等式的性质解方程,即等式两边同时加、减、乘同一个数或除以同一个不为0的数,等式的左右两边仍相等;注意等号上下要对齐.
29.【分析】总页数﹣每天看的页数×看的天数=没看的页数,把数据代入含字母的式子中,求值即可。
【解答】解:300﹣7×x=(300﹣7x)页
当x=25时,
300﹣7×25
=300﹣175
=125(页)
答:这本书还剩(300﹣7x)页没看;当x=25时,还剩125页没看。
【点评】此题的关键是明确:总页数﹣看了的页数=没看的页数,把没看的页数表示出来,然后再进一步解答。
30.【分析】淘米→煮饭(同时洗菜、切菜、炒菜),据此计算即可。
【解答】解:3+30=33(分钟)
答:妈妈要将饭菜都做好,最少要用33分钟。先淘米,再煮饭,煮饭的同时洗菜、切菜、炒菜。
【点评】此题的关键是明确哪些事可以同时做,然后再进一步解答。
31.【分析】根据题意可知,跑同样的路程,用时越少,速度越快,名次越高,然后根据小数大小比较的方法进行解答即可。
【解答】解:8.9<9.1<9.4
所以第一名是王丽;第二名是李红;第三名是刘英。
【点评】本题主要考查小数大小的比较,关键是根据小数大小比较的方法做题。
32.【分析】在每次能同时放2个烧饼的情况下,根据“烤每面的时间×个数=时间”代入数据解答即可。
【解答】解:2×5=10(分钟)
答:烤熟5个烧饼至少需要10分钟。
【点评】煎饼的数量是偶数个时,就按照每两张饼一组求解;奇数个时,先拿出3张,剩下的再按照2张一组求解。
一.选择题
1.五年级种树60棵,比四年级种的2倍少4棵。四年级种树多少棵?设四年级种树x棵,下列方程错误的是( )。
A.2x=60﹣4 B.2x﹣4=60 C.2x=60+4 D.60+4=2x
2.下面各组式子中,不一定相等的是( )
A.4a和a+a+a+a B.a2和a+a
C.a2和a×a
3.如图,天平平衡了,下列数量关系正确的是( )
A.3m=2n B.m=2n C.n=2m
4.方程一词,最早出现在我国古代数学书籍《九章算术》中。下列式子是方程的是( )
A.3x+2y B.5x÷6>3 C.5×3=15 D.a﹣2=7
5.已知3x+2=11,那么4x﹣1=( )
A.9 B.13 C.11
6.五年级植树120棵,比三年级植树棵数的3倍多6棵,三年级植树多少棵?设三年级植树x棵,下列方法错误是( )
A.3x+6=120 B.3x﹣6=120 C.120﹣3x=6 D.3x=120﹣6
7.在下面给出的平面图形中,不能进行密铺的是( )
A.三角形 B.四边形 C.正七边形
8.学校组织体检,三位小朋友量得的身高如下,身高最高的是( )
A.1.24米 B.1.4米 C.1.54米
二.填空题
9.故宫的面积是72万平方米,比天安门广场面积的2倍少16万平方米。设天安门广场的面积是x万平方米,根据题意写出一个等量关系式:
,根据这个等量关系式写出相应的方程 。
10.果园有梨树540棵,比桃树的4倍还多20棵,果园里有桃树 棵。
11.天平左端放着一块巧克力,右端放着同样的巧克力半块和50克的砝码,这时天平恰好平衡.一块巧克力的重量是 克.
12.一只平底锅只能同时煎2条鱼,用它煎一条鱼需要4分钟(正、反面各2分钟),那么煎5条鱼至少需要 分钟。
13.在3.78、3.7888……、3.、3.7、3.五个数中,最大的是 ,最小的是 ,3.7精确到十分位是 。
14.请你写出两种能密铺的图形 、 。
15.如图,如果要拿掉桃子x克,则天平的右边需要拿掉 个砝码,使天平继续保持平衡。
16.如果a=b,根据等式的性质则:a﹣c=b﹣ ,a÷2=b÷ 。
17.根据图中的数量关系列出方程是 。
18.一本《三国演义》一共有x页,小红每天看a页,看了5天。一共看了 页,还有 页没看。
三.判断题
19.m2=m×2。
20.等式两边乘或除以同一个数,左右两边仍然相等。
21.8x+6是方程。
22.若3x+y=8,则9x+3y=24。
23.小明家的平底锅一次能同时烙2张饼,烙一张饼需要6分钟(正反面各3分钟),小明用27分钟的时间最多可以烙8张饼。
四.计算题
24.求铅笔和钢笔本各有多少支?
25.解方程。
x÷8=0.4 5x+28=48 3x﹣4×6=48
五.应用题
26.森林公园的面积是61公顷,比青年广场面积的4倍多9公顷,青年广场的面积是多少公顷?(用方程解)
27.学校组织五、六年级同学听抗疫英雄巡回演讲会,一共有972人。报告厅每排可以坐18人,五年级坐了26排,六年级坐了多少排?(列方程解答)
28.若方程2x+3=21与5x﹣m=30的解相同,则m是多少?
29.小芳看一本300页的故事书,她每天看x页,已经看了7天,先用式子表示这本书还剩多少页没看?再计算当x=25时,还剩多少页没看?
30.妈妈回家做饭,淘米要3分钟,煮饭要30分钟,洗菜要8分钟,切菜要5分钟,炒菜要10分钟。如果煮饭和炒菜要用不同的锅和炉子,妈妈要将饭菜都做好,最少要用多长时间,说明你的想法。
31.在60米短跑比赛中,前三名当中李红的成绩是9.1秒,刘英的成绩是9.4秒,王丽的成绩是8.9秒.请你把她们比赛的名次排出来.
32.电饼铛里每次能同时放2个烧饼,如果烧熟1个烧饼的正反两面各需要2分,那么烤熟5个烧饼至少需要多少分?
参考答案
一.选择题
1.【分析】四年级种树的棵树×2﹣4=五年级种树的棵树,据此等量关系列出方程即可。
【解答】解:2x﹣4=60
2x﹣4+4=60+4
2x=64
2x÷2=64÷2
x=32
答:四年级种树32棵。
故选:A。
【点评】根据题意找出等量关系,列出方程即可解决此题。
2.【分析】4a=4×a=a+a+a+a,A项两个式子一定相等;a2=a×a,C项两个式子一定相等,B项两个式子不一定相等。
【解答】解:不一定相等的是a2和a+a。
故选:B。
【点评】此题的关键是明确带字母式子的意义,然后再进一步解答。
3.【分析】天平平衡了,说明两边的总量相等。也就是m+m+m=m+n,两边同时减去m可得2m=n,据此解答。
【解答】解:m+m+m=m+n
m+m+m﹣m=m+n﹣m
2m=n
数量关系正确的是n=2m。
故选:C。
【点评】此题的关键是明确天平平衡时两边总量相等,然后再进一步解答。
4.【分析】方程是指含有未知数的等式;所以方程必须具备两个条件:①含有未知数;②等式。据此解答。
【解答】解:3x+2y、5x÷6>3不是等式;
5×3=15不含有未知数;
a﹣2=7含有未知数,是等式,是方程。
故选:D。
【点评】此题考查方程的辨识:只有含有未知数的等式才是方程。
5.【分析】根据等式的性质,先求出方程3x+2=11的解,然后再代入4x﹣1求出值即可。
【解答】解:3x+2=11
3x+2﹣2=11﹣2
3x=9
3x÷3=9÷3
x=3
把x=3代入4x﹣1可得:
4×3﹣1=11。
故选:C。
【点评】本题关键是根据等式的性质求出方程的解,然后再代入含有未知数的式子求出值。
6.【分析】这道题的等量关系非常明显,三年级植树的棵数×3+6棵=五年级植树的棵数120,由此设出三年级植树x棵,列出方程解答即可。
【解答】解:A.根据三年级植树的棵数×3+6棵=五年级植树的棵数120,可得3x+6=120,本项不符合题意;
B.3x﹣6=120错误,本项符合题意;
C.根据五年级植树的棵数120﹣三年级植树的棵数×3=6棵,可得120﹣3x=6,本项不符合题意;
D.根据三年级植树的棵数×3=五年级植树的棵数(120﹣6)棵,可得3x=120﹣6,本项不符合题意。
故选:B。
【点评】解决这类问题主要找出题里面蕴含的数量关系,由此列出方程解决问题。
7.【分析】几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角;360°为正多边形一个内角的整数倍才能单独镶嵌。
【解答】解:在上面给出的平面图形中,不能进行密铺的是正七边形,三角形和四边形能进行密铺。
故选:C。
【点评】本题考查了平面镶嵌(密铺),用一种正多边形镶嵌,只有三角形、四边形、六边形三种正多边形能镶嵌成一个平面图案。
8.【分析】比较小数的大小时,要先比较整数部分的位数,它们的数位如果不同,那么数位多的那个数就大,如果数位相同,相同数位上的数大的那个数就大;如果整数部分相同,然后再比较小数部分的十分位、百分位、千分位……;据此解答即可。
【解答】解:1.24<1.4<1.54
所以身高最高的是1.54米。
故选:C。
【点评】此题考查了小数大小比较方法的灵活运用。
二.填空题
9.【分析】由题意可以得到数量关系:天安门广场的面积×2﹣16=故宫的面积,设出天安门广场的面积,依据得到的等量关系,即可列出符合题意的方程。
【解答】解:设天安门广场的面积是x万平方米,天安门广场的面积×2﹣16=故宫的面积,
2x﹣16=72
2x=88
x=44
故答案为:天安门广场的面积×2﹣16=故宫的面积,2x﹣16=72。
【点评】解答此题的关键是:依据题意,把一倍的量设为未知数,然后找出等量关系,即可列出方程。
10.【分析】设桃树有x棵,依据题意桃树棵数×4+20棵=梨树棵数可列方程:4x+20=540,依据等式的性质即可求解。
【解答】解:设桃树有x棵
4x+20=540
4x+20﹣20=540﹣20
4x÷4=520÷4
x=130
答:果园里有桃树130棵。
故答案为:130。
【点评】解答本题的关键是依据题意列出方程,解答依据是等式的性质。
11.【分析】根据题意得出一块巧克力的重量=半块巧克力的重量+50,由此得出半块巧克力的重量,进而求出一块巧克力的重量.
【解答】解:根据题意得出半块巧克力的重量是50克,
所以1块巧克力的重量为:50×2=100(克),
答:一块巧克力的重量是100克;
故答案为:100.
【点评】关键是根据题意求出半块巧克力的重量是50克,进而解决问题.
12.【分析】烙饼问题公式:总时间=饼数×2÷每锅的可烙的数量×烙每面的时间。把XX看作饼,代入公式计算即可。
【解答】解:5×2÷2×2
=5×2
=10(分钟)
答:煎5条鱼至少需要10分钟。
故答案为:10。
【点评】此题考查了烙饼问题的应用,要熟记公式。
13.【分析】根据小数大小比较的方法:比较两个小数的大小,先看它们的整数部分,整数部分大的那个数就大,整数部分相同的,十分位上的数大的那个数就大,十分位上的数也相同的,百分位上的数大的那个数就大直接比较可得;精确到十分位就要看小数点后面第二位,再根据“四舍五入“法取近似数即可。
【解答】解:因为3.7888……>3.>3.78>3.>3.7
所以在3.78、3.7888……、3.、3.7、3.五个数中,最大的是3.7888…,最小的是3.7;
3.7≈3.7
所以3.7精确到十分位是 3.7。
故答案为:3.7888……,3.7,3.7。
【点评】此题主要考查了小数比较大小的方法的应用以及根据“四舍五入”
法求近似数,要熟练掌握。
14.【分析】平面图形密铺的特点:(1)用一种或几种全等图形进行拼接;(2)拼接处不留空隙、不重叠; (3)连续铺成一片。能密铺的图形在一个拼接点处的特点是:几个图形的内角拼接在一起时,其和等于360°,并使相等的边互相重合。圆、半圆、正五边形就不具备这样的特点。
【解答】解:两种能密铺的图形是正方形和正六边形。
故答案为:正方形和正六边形。(答案不唯一)
【点评】考查了平面镶嵌(密铺)问题,两种或两种以上几何图形镶嵌成平面的关键是:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角。
15.【分析】天平平衡则有300+x=500,再根据等式的基本性质可求得x的质量,右边5个砝码是500克,据此可算出一个砝码是100克,据此解答即可。
【解答】解:300+x=500
300+x﹣300=500﹣300
x=200
500÷5=100(克)
200÷100=2(个)
【点评】熟练掌握等式的基本性质是解题的关键。
16.【分析】等式的基本性质1:等式两边同时加上(或减去)同一个数,等式仍然成立;
等式的基本性质2:等式两边同时乘(或除以)同一个不为0的数,等式仍然成立,据此计算即可。
【解答】解:a=b
a﹣c=b﹣c
a=b
a÷2=b÷2
【点评】熟练掌握等式的基本性质是解题的关键。
17.【分析】每只小猴子分到的个数×小猴子的只数=桃子总数,据此列方程即可。
【解答】解:根据图中的数量关系列出方程是3a=48。
故答案为:3a=48。
【点评】列方程解应用题,关键是根据题意找出基本数量关系,正确列出方程。
18.【分析】每天看a页,看了5天,则一共看了(5×a)页,用总页数减去看了的页数就是没看的页数。
【解答】解:一共看了5a页,还有(x﹣5a)页没看。
故答案为:5a,(x﹣5a)。
【点评】此题的关键是先求出看了的页数,然后再进一步解答。
三.判断题
19.【分析】m2=m×m,据此判断即可。
【解答】解:m2=m×m,
故原题说法错误。
故答案为:×。
【点评】此题主要考查了平方的意义,要熟练掌握。
20.【分析】等式两边同时乘或除以同一个不为0的数,等式仍然成立。
【解答】解:题干没有强调除以不为0的数。
故原题说法错误。
故答案为:×。
【点评】此题考查了等式的性质,要熟练掌握。
21.【分析】方程是指含有未知数的等式;所以方程必须具备两个条件:①含有未知数;②等式。据此解答。
【解答】解:8x+6不是等式,因此不是方程。
故原题说法错误。
故答案为:×。
【点评】此题考查方程的辨识:只有含有未知数的等式才是方程。
22.【分析】等式两边同时加上(或减去)同一个数,等式仍然成立。等式两边同时乘或除以同一个不为0的数,等式仍然成立。
【解答】解:若3x+y=8,则等式两边同时乘3,可以得到9x+3y=24。
故原题说法正确。
故答案为:√。
【点评】此题考查了等式的性质,要熟练掌握。
23.【分析】烙饼问题公式:总时间=饼数×2÷每锅的可烙的数量×
烙每面的时间,代入公式计算并比较即可。
【解答】解:8×2÷2×3
=8×3
=24(分钟)
24<27
9×2÷2×3
=9×3
=27(分钟)
小明用27分钟的时间最多可以烙9张饼。
故原题说法错误。
故答案为:×。
【点评】此题考查了烙饼问题的应用,要熟记公式。
四.计算题
24.【分析】根据题意,设铅笔有x支,则钢笔为(2x﹣2)支,有关系式:铅笔支数+钢笔支数=10支,列方程求解即可求出铅笔支数,再求钢笔即可.
【解答】解:设铅笔有x'支,
x+2x﹣2=10
3x=12
x=4
4×2﹣2
=8﹣2
=6(支)
答:铅笔有4支,钢笔有6支.
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题.
25.【分析】(1)根据等式的基本性质,方程两边同时乘8即可;
(2)根据等式的基本性质,方程两边同时减去28,两边再同时除以5;
(3)根据等式的基本性质,方程两边同时加上24,两边再同时除以3。
【解答】解:(1)x÷8=0.4
x÷8×8=0.4×8
x=3.2
(2)5x+28=48
5x+28﹣28=48﹣28
5x=20
5x÷5=20÷5
x=4
(3)3x﹣4×6=48
3x﹣4×6+24=48+24
3x=72
3x÷3=72÷3
x=24
【点评】熟练掌握等式的基本性质是解题的关键。
五.应用题
26.【分析】设青年广场的面积是x公顷,根据等量关系:青年广场面积×4+9公顷=森林公园的面积,列方程解答即可。
【解答】解:设青年广场的面积是x公顷,
4x+9=61
4x=52
x=13
答:青年广场的面积是13公顷。
【点评】本题考查了列方程解应用题,关键是根据等量关系:青年广场面积×4+9公顷=森林公园的面积列方程。
27.【分析】根据题意,设六年级坐了x排;根据题意可得:(五年级坐的排数+六年级坐的排数)×每排坐的人数=总人数,据此列出方程进行解答。
【解答】解:设六年级坐了x排,根据题意可得:
(26+x)×18=972
(26+x)×18÷18=972÷18
26+x=54
26+x﹣26=54﹣26
x=28
答:六年级坐了28排。
【点评】列方程解决实际问题,关健是根据题意设出未知数,找出等量关系,然后再列出方程进行解答。
28.【分析】方程2x+3=21,根据等式的性质,方程两边同时减去3,再两边同时除以2,求出x的值;再把x的值代入5x﹣m=30求出m是多少即可.
【解答】解:2x+3=21
2x+3﹣3=21﹣3
2x=18
2x÷2=18÷2
x=9
把x=9代入5x﹣m=30
5×9﹣m=30
45﹣m=30
45﹣m+m=30+m
45=30+m
45﹣30=30+m﹣30
m=15
答:m是15.
【点评】此题考查了根据等式的性质解方程,即等式两边同时加、减、乘同一个数或除以同一个不为0的数,等式的左右两边仍相等;注意等号上下要对齐.
29.【分析】总页数﹣每天看的页数×看的天数=没看的页数,把数据代入含字母的式子中,求值即可。
【解答】解:300﹣7×x=(300﹣7x)页
当x=25时,
300﹣7×25
=300﹣175
=125(页)
答:这本书还剩(300﹣7x)页没看;当x=25时,还剩125页没看。
【点评】此题的关键是明确:总页数﹣看了的页数=没看的页数,把没看的页数表示出来,然后再进一步解答。
30.【分析】淘米→煮饭(同时洗菜、切菜、炒菜),据此计算即可。
【解答】解:3+30=33(分钟)
答:妈妈要将饭菜都做好,最少要用33分钟。先淘米,再煮饭,煮饭的同时洗菜、切菜、炒菜。
【点评】此题的关键是明确哪些事可以同时做,然后再进一步解答。
31.【分析】根据题意可知,跑同样的路程,用时越少,速度越快,名次越高,然后根据小数大小比较的方法进行解答即可。
【解答】解:8.9<9.1<9.4
所以第一名是王丽;第二名是李红;第三名是刘英。
【点评】本题主要考查小数大小的比较,关键是根据小数大小比较的方法做题。
32.【分析】在每次能同时放2个烧饼的情况下,根据“烤每面的时间×个数=时间”代入数据解答即可。
【解答】解:2×5=10(分钟)
答:烤熟5个烧饼至少需要10分钟。
【点评】煎饼的数量是偶数个时,就按照每两张饼一组求解;奇数个时,先拿出3张,剩下的再按照2张一组求解。
