北师大版五年级下册数学单元测试-第7单元用方程解决问题(含答案)
文档属性
| 名称 | 北师大版五年级下册数学单元测试-第7单元用方程解决问题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 94.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 14:06:54 | ||
图片预览



文档简介
第7单元 用方程解决问题+数学好玩
一.选择题
1.下面题目不能用方程4x+5=69来解决的是( )
A.合唱队有69人,比舞蹈队人数的4倍多5人,舞蹈队有x人
B.有69千克橙子,装了4箱,还剩5千克,平均每箱装x千克
C.爸爸体重69千克,再长5千克就是芳芳体重的4倍了,芳芳体重x千克
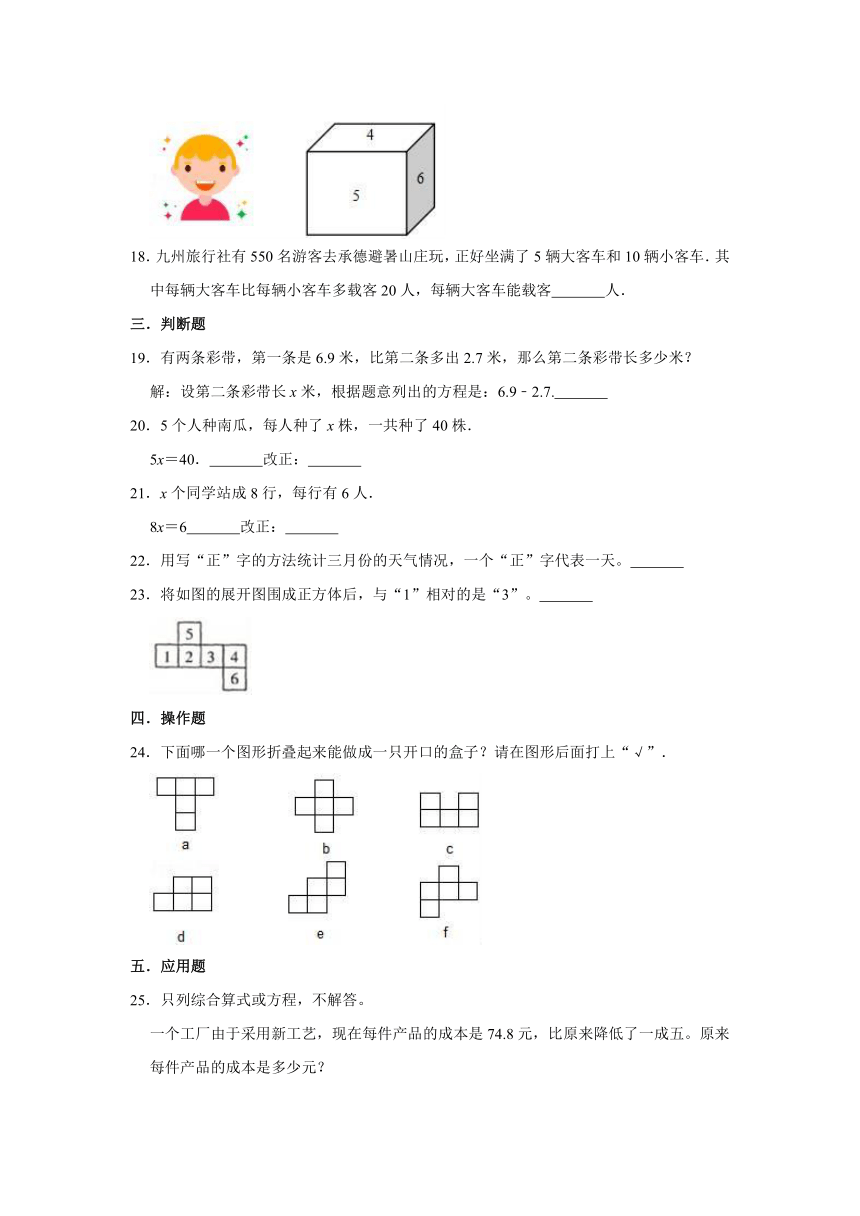
2.甲、乙两队合修一段长1400m的公路。两队同时从两头开工,5天修完。已知甲队平均每天修160m,乙队平均每天修多少米?设乙队平均每天修工xm,下列式子中正确的有( )个。
160×5+x=1400 5×(160+x) 1400÷(160+x)
1400÷5=160+x (1400﹣160×5)÷x=5 1400÷5﹣x=160
A.3 B.4 C.5 D.6
3.甲,乙两人从相距20千米的两地出发相向而行,一只小狗与甲同时出发向乙奔去,遇到乙后立即掉头向甲跑去,遇到甲后又立即掉头向乙跑去…直到甲乙两人相遇为止.已知甲的速度是6千米/小时,乙的速度是4千米/小时,小狗的速度是13千米/小时,在这一过程中,小狗共跑了( )千米.
A.18 B.20 C.24 D.26
4.如图,A、B是圆的直径的两端,小张在A点,小王在B点同时出发,相向行走,他们在距A点80米处的C点第一次相遇,接着又在距B点60米处的D点第二次相遇.那么,这个圆的周长是( )米.
A.140 B.240 C.180 D.360
5.李老师要为图书馆购置一批图书,他需要先调查( )。
A.同学们每天阅读多长时间
B.同学们在家会阅读吗
C.同学们喜欢哪几类课外书
D.同学们本学期读了几本课外书
6.如图是长方体的表面展开图,折叠成一个长方体后,那么与字母J重合的点是( )
A.H和N B.N和M C.B和H D.和N
7.下面哪个图形沿虚线对折不能围成正方体( )
A. B.
C.
8.张大爷家收了780千克苹果,装了30筐,还剩下15千克.平均每筐装x千克,下面的方程中,错误的是( )
A.780﹣30x=15 B.30x+15=780 C.30x﹣15=780
二.填空题
9.根据数量关系列出方程。(不用求解)
(1)爸爸今年x岁,小刚今年12岁,小刚比爸爸小26岁。
(2)果园里种着桃树x棵,杏树的棵数是桃树的3倍,杏树比桃树多90棵。
10.小明买了12支彩笔,每支彩笔x元,付给售货员20元,找回了2元.
+ =20元
方程: .
11.在如图中描出长度是(150+x)的一段。x= 。
12.西安大雁塔高约64米,比小雁塔高度的2倍少22米。写出等量关系式是 。
13.根据题意把方程补充完整.
甲、乙两辆汽车同时从相距270千米的两地相对开出3小时后相遇,甲车每小时行驶48千米,乙车每小时行驶多少千米?
(1)根据甲车行驶的路程+乙车行驶的路程=总路程,设乙车每小时行驶x千米,列方程: + =270
(2)根据(甲车每小时行驶的路程+乙车每小时行驶的路程)×3=总路程,设乙车每小时行驶x千米,列方程:
( + )×3=270
14.甲乙两人同时从A地走向B地,甲的速度是每分钟90米,乙的速度是每分钟80米,甲到达A地后立即返回,途中距离B地180米处与乙相遇,问乙走的路程是全程的 .
15.甲、乙两人分别从A、B两地同时出发,相向而行,他们相遇时,甲比乙多行90米,相遇后乙的速度减少50%,甲到B地后立即调头,追上乙时离A地还有90米,那么A、B两地间的距离为 米。
16.右面是一个无盖的长方体纸盒的展开图.与④号面相对的面是 号面,纸盒的底面是 号面.
17.写一写。
相对的两个面上的数字之和为7。
看到的数字是 。
18.九州旅行社有550名游客去承德避暑山庄玩,正好坐满了5辆大客车和10辆小客车.其中每辆大客车比每辆小客车多载客20人,每辆大客车能载客 人.
三.判断题
19.有两条彩带,第一条是6.9米,比第二条多出2.7米,那么第二条彩带长多少米?
解:设第二条彩带长x米,根据题意列出的方程是:6.9﹣2.7.
20.5个人种南瓜,每人种了x株,一共种了40株.
5x=40. 改正:
21.x个同学站成8行,每行有6人.
8x=6 改正:
22.用写“正”字的方法统计三月份的天气情况,一个“正”字代表一天。
23.将如图的展开图围成正方体后,与“1”相对的是“3”。
四.操作题
24.下面哪一个图形折叠起来能做成一只开口的盒子?请在图形后面打上“√”.
五.应用题
25.只列综合算式或方程,不解答。
一个工厂由于采用新工艺,现在每件产品的成本是74.8元,比原来降低了一成五。原来每件产品的成本是多少元?
26.养猪专业户王大伯说:“如果卖掉130头猪,那么饲料可维持20天;如果买进110头猪,那么饲料只能维持15天.”问:王大伯一共养了多少头猪?
27.小华和小兰同时从相距1080米的两地相向而行,小华每分钟走72米,小兰每分钟走63米,经过多少分钟两人相遇?(用方程解)
28.“半条被子”发生地汝城县沙洲村今年9月份以来平均每个月接待游客约8600人次,比去年同期的3倍还多200人。去年同期平均每个月接待游客约多少人?(用方程解)
29.正方体有6个面,每个面上分别写有1个数字,它们是1、2、3、4、5、6,而且每个相对面上两个数的和是7(1和6,2和5,3和4).如图是正方体六个面的展开图,请填出空格内的数.
30.快车和慢车同时从两地相向而行,4时后在距中点48千米处相遇.已知慢车每时行60千米,两地相距多少千米?
31.甲、乙两个工程队同时开凿一条360m长的隧道,各从一端相向施工,4天打通。甲队每天开凿的长度是乙队的1.25倍,甲、乙两队每天各开凿多少米?(用方程解答)
参考答案
一.选择题
1.【分析】A.舞蹈队人数为x人,根据等量关系:舞蹈队人数×4+5人=合唱队人数,列方程即可;
B.平均每箱装x千克,根据等量关系:平均每箱千克数×4+5千克=总千克数,列方程即可;
C.芳芳体重x千克,根据等量关系:芳芳体重×4﹣5千克=爸爸体重,列方程即可。
【解答】解:A.舞蹈队人数为x人,4x+5=69,本项不符合题意;
B.平均每箱装x千克,4x+5=69,本项不符合题意;
C.芳芳体重x千克,4x﹣5=69,本项符合题意。
故选:C。
【点评】解决这类问题主要找出题里面蕴含的数量关系,由此列出方程解决问题。
2.【分析】上面三个算式不是方程只是含有未知数的式子因此不符合方程的定义;
(4)依据甲和乙的工作效率和=甲的工作效率+乙的工作效率列方程判断;
(5)依据乙的工作量工作时间=(工作总量﹣甲的工作量)÷乙的工作量列方程判断;
(6)依据工作总量÷工作时间﹣乙的工作效率=甲的工作效率列方程判断。
【解答】解:(1)“160×5+x=1400”依据甲5天的工作总量+乙5天的工作总量=1400,但是乙只加了一天的,所以错误。
(2)“5×(160+x)”只是含有字母的式子,不能表达完整的要解决问题,解决问题没有完成。
(3)“1400÷(160+x)”是含有字母的式子,不能表达完整的要解决问题,解决问题没有完成。
(4)1400÷5=160+x,表示甲和乙的工作效率和=甲的工作效率+乙的工作效率,方程成立。
(5)(1400﹣160×5)÷x=5表示乙的工作量工作时间=(工作总量﹣甲的工作量)÷乙的工作量,方程成立。
(6)1400÷5﹣x=160表示工作总量÷工作时间﹣乙的工作效率=甲的工作效率,方程成立。
故选:A。
【点评】列方程解应用题的步骤:
①弄清题意,确定未知数,并用x表示。
②找出题中数量之间的相等关系。
③列方程,解方程。
④检查或验算,写出答案。
3.【分析】根据题意,甲、乙相遇需要的时间是20÷(6+4)=2(小时),在此过程中狗一直奔跑,所以狗跑的时间也是2小时,然后根据狗的速度,运用关系式:速度×时间=路程,解决问题.
【解答】解:20÷(6+4)×13
=2×13
=26(千米)
答:在这一过程中,小狗共跑了26千米.
故选:D.
【点评】此题解答的关键是要知道:甲、乙相遇需要的时间就是狗跑的时间.
4.【分析】两人第一次相遇时,共行了半个周长,此时小张行了80米,即每共行半个圆,小张就走80米,离开C点,第二次相遇时,两共行了3个半圆,则此时小张A从C点到D点行了80 3=240米,又B点距D点为60米,则A到B点长240﹣60=180米,所以周长是180×2=360米.
【解答】解:(80×3﹣60)×2
=(240﹣60)×2,
=180×2,
=360(米).
答:这个圆的周长是 360米.
故选:D.
【点评】根据题意得出每共行半个圆,小张就走80米是完成本题的关键.
5.【分析】李老师要为图书馆购置一批图书,首先要明确买什么种类的书,买多少书,据此解答。
【解答】解:李老师要为图书馆购置一批图书,首先要明确买什么种类的书,因此得先调查同学们的喜好。
故选:C。
【点评】解答此题的关键是理解必备的条件是什么。
6.【分析】根据长方体展开图的特征可知,与字母J重合的点是N和H。据此解答。
【解答】解:如图是长方体的表面展开图,折叠成一个长方体后,那么与字母J重合的点是N和H。
故选:A。
【点评】此题考查的目的是理解掌握长方体展开图的特征及应用。
7.【分析】根据正方体展开图的类型,1﹣4﹣1型,2﹣3﹣1型,2﹣2﹣2型,3﹣3型,据此解答即可.
【解答】解:A、B都是正方体的展开图,属于1﹣4﹣1型,能折成长方体;
C不是正方体的展开图,不能折成长方体;
故选:C.
【点评】本题是考查正方体的展开图,是培养学生的观察、分析能力和空间想象能力.此类题可动手折叠一下,即可解决问题,又锻炼了动手操作能力.
8.【分析】根据题干,设平均每筐装x千克,则可得等量关系:平均每筐装的千克数×筐数+剩下的15千克=苹果的总千克数,或者苹果的总千克数﹣平均每筐装的千克数×筐数=剩下的15千克,列出的方程是:30x+15=780或者780﹣30x=15,据此即可焦点问题.
【解答】解:设平均每筐装x千克,根据题意可得方程:
30x+15=780或者780﹣30x=15
所以上面的方程错误的是30x﹣15=780.
故选:C.
【点评】解答此题容易找出基本数量关系:平均每筐装的千克数×筐数+剩下的15千克=苹果的总千克数,或者苹果的总千克数﹣平均每筐装的千克数×筐数=剩下的15千克,由此列方程解决问题.
二.填空题
9.【分析】(1)本题的数量关系式是:爸爸的年龄﹣小刚的年龄=小刚比爸爸小的,据此我们设爸爸今年x岁,列出的方程就是:x﹣12=26;
(2)根据题意我们知道:杏树的棵数×3=桃树的棵数,如果桃树有x
棵,那么杏树的棵数就用3x来表示,还知道杏树的棵数﹣桃树的棵数=90,据此列出的方程就是:3x﹣x=90。
【解答】解:(1)爸爸今年x岁,小刚今年12岁,小刚比爸爸小26岁。
x﹣12=26
(2)果园里种着桃树x棵,杏树的棵数是桃树的3倍,杏树比桃树多90棵。
3x﹣x=90
故答案为:(1)x﹣12=26;(2)3x﹣x=90。
【点评】观察题干,分析数量关系,设出未知数列方程即可。
10.【分析】设每支彩笔x元,则根据等量关系:彩笔的价格×12+找回的2元=付出的钱数20元,据此列出方程解决问题.
【解答】解:设每支彩笔x元,则根据等量关系:彩笔的价格×12+找回的2元=付出的钱数20元,据此列出方程是:
12x+2=20
12x=18
x=1.5
答:每支彩笔1.5元.
故答案为:彩笔的价格×12;找回的2元;12x+2=20.
【点评】解答此题容易找出基本数量关系,由此列方程解决问题.
11.【分析】根据图意,图中(150+x)的一段是200米,可以列出方程:150+x=200,求出方程的解即可。
【解答】解:150+x=200
150+x﹣150=200﹣150
x=50
故答案为:50。
【点评】本题考查列方程求解的问题,解题关键是找出题目中的等量关系列方程解答。
12.【分析】根据题意可知,小雁塔的高×2﹣22米=大雁塔的高64米,据此解答即可。
【解答】解:等量关系式是:小雁塔的高×2﹣22米=大雁塔的高64米。
故答案为:小雁塔的高×2﹣22米=大雁塔的高64米。
【点评】解答此题,首先弄清题意,分清已知与所求,再找出基本的等量关系。
13.【分析】(1)根据题干,设乙车每小时行驶x千米,根据等量关系:甲车行驶的路程+乙车行驶的路程=总路程,列出方程为:48×3+3x=270,据此即可解答问题;
(2)根据题干,设乙车每小时行驶x千米,根据等量关系:(甲车每小时行驶的路程+乙车每小时行驶的路程)×3=总路程,列出方程为:(48+x)×3=270,解除即可解答问题.
【解答】解:(1)设乙车每小时行驶x千米,根据题意可得:
48×3+3x=270
144+3x=270
3x=126
x=42
答:乙车每小时行驶42千米.
(2)设乙车每小时行驶x千米,根据题意可得:
(48+x)×3=270
48+x=90
x=42
答:乙车每小时行驶42千米.
【点评】此题主要考查相遇问题中的基本数量关系:甲车所行的路程+乙车所行的路程=两地之间的距离或速度和×相遇时间=总路程;再由关系式列方程解决问题.
14.【分析】根据题意可知:甲比乙多行180×2=360(米),利用追及问题公式:追及时间=路程差÷速度差,把数代入计算得:360÷(90﹣80)=36(分钟);然后利用公式:路程=速度×时间,求乙所行路程及全程,即可求解.
【解答】解:180×2÷(90﹣80)×80
=360÷10×80
=36×80
=32880(米)
2880÷(2880+180)
=2880÷3060
≈94%
答:乙走的路程是全程的 94%.
故答案为:94%.
【点评】本题主要考查相遇问题,关键利用路程、速度和时间的关系做题.
15.【分析】画出线段图,设A,B两地的距离为2a米,相遇时甲比乙多行90米,也就是甲走了(a+45)米,乙走了(a﹣45)米,他们的速度比为(a+45):(a﹣45),乙降速后两人的速度比变为(a+45):=2(a+45):(a﹣45),追及时,甲走的路程为a﹣45+2a﹣90=3a﹣135(米),乙走的路程为a+45﹣90=a﹣45(米),根据追及时,路程比等于速度比,列出方程求解即可。
【解答】解:线段图:
设A,B两地的距离为2a米,
相遇时甲比乙多行90米,
也就是甲走了(a+45)米,乙走了(a﹣45)米,
他们的速度比为(a+45):(a﹣45),
乙降速后两人的速度比变为(a+45):=2(a+45):(a﹣45),
追及时,甲走的路程为a﹣45+2a﹣90=3a﹣135(米),乙走的路程为a+45﹣90=a﹣45(米),
根据追及时,路程比等于速度比,
=
3a﹣135=2a+90
a=225
2a=450
答:A、B两地间的距离为450米。
故答案为:450。
【点评】本题主要考查了相遇与追及问题的综合,把握相遇问题和追及问题中,路程比等于速度比,是本题解题的关键。
16.【分析】根据长方体的特征,长方体6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相对。通过观察这个长方体的展开图可知,与④号面相对的面①
号,③号面与⑤号面相对,由此可知,这个纸盒的底面是②号面。据此解答。
【解答】解:通过观察长方体的展开图可知,与④号面相对的面①号,③号面与⑤号面相对,所以这个纸盒的底面是②号面。
答:这个无盖纸盒的底面是②号面。
故答案为:①、②。
【点评】此题考查的目的是理解掌握长方体展开图的特征及应用。
17.【分析】根据题意和图示可知,相对的两个面上的数字之和为7,那么图中的已知的数字5的对面就是2,6的对面的数字是1,4的对面的数是3,看看图中小男孩站的位置,据此解答。
【解答】解:小男站的位置是正方体的左面,根据正方体右边的数字是6,可以推出7﹣6=1,因此小男孩看到是数字是1。
故答案为:1。
【点评】解答此题的关键理解相对的面的意思。
18.【分析】根据题意可知,5辆大客车载客的人数+10辆小客车载客的人数=550人,已知每辆大客车比每辆小客车多载客20人,设每辆大客车能载客x人,则每辆小客车能载(x﹣20)人,据此列方程解答.
【解答】解:设每辆大客车能载客x人,则每辆小客车能载(x﹣20)人,
5x+(x﹣20)×10=550
5x+10x﹣200=550
15x﹣200=550
15x﹣200+200=550+200
15x=750
15x÷15=750÷15
x=50
答:每辆大客车能载客50人.
故答案为:50.
【点评】解决这类问题主要找出题里面蕴含的等量关系,设出未知数,由此列出方程解决问题.
三.判断题
19.【分析】根据题意可知,第二条的长度+2.7米=第一条的长度(9.6米),或第二条的长度=第一条的长度(9.6米)减去2.7米。设第二条彩带长为x米,据此可方程:x+2.7=9.6,或x=9.6﹣2.7。据此判断。
【解答】解:设第二条彩带长为x米,据此可方程:x+2.7=9.6。
所以原题的说法错误。
故答案为:×。
【点评】此题考查的目的理解掌握方程的意义及应用,明确:含有未知数的等式叫做方程。
20.【分析】根据题意,分析数量关系,可得等量关系式:每人种的株数×人数=总株数,然后设每人种了x株,再列方程解答即可.
【解答】解:设每人种了x株,
5x=40
5x÷5=40÷5
x=8
答:每人种了8株.
故答案为:√,﹣﹣﹣﹣.
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题.
21.【分析】根据题意,分析数量关系,可得等量关系式:每行的人数=总人数÷行数,然后设有x个同学,再列方程解答即可.
【解答】解:设有x个同学,
x÷8=6
x=8×6
x=48
答:有48个同学.
故答案为:×,x÷8=6.
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题.
22.【分析】正”有5笔,每一笔表示1个统计量,由此判断。
【解答】解:用写“正”字的方法统计三月份的天气情况,一个“正”字代表5天;
原题说法错误。
故答案为:×。
【点评】本题考查了用“正”字表示统计量的方法,一个“正”字表示5。
23.【分析】根据正方体展开图的11种特征,此图属于正方体展开图的“1﹣4﹣1”型,折成正方体后,“1”与“3”相对,“2”与“4”相对,“5”与“6”相对。
【解答】解:如图
围成正方体后,与“1”相对的是“3”。
原题说法正确。
故答案为:√。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住,能快速解答此类题。
四.操作题
24.【分析】a、b、f属于正方体展开图的“1﹣4﹣1”型,去掉一个“1”,能做成一只开口的盒子;c、d在任何添上一个正方形都不是正方体展开图,不能做成一只开口的盒子;e属于正方形展开图的“1﹣3﹣2”型,去掉“3”中的一个正方开,能做成一只开口的盒子.
【解答】解:下面哪一个图形折叠起来能做成一只开口的盒子?请在图形后面打上“√”.
【点评】关键记住正方体展开图的11种情况:正方体展开图分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣
2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.
五.应用题
25.【分析】降低一成五就是指比原来降低了15%,设原来每件产品的成本是x元,根据等量关系:原来每件产品的成本×(1﹣15%)=现在每件产品的成本,列方程解答即可。
【解答】解:设原来每件产品的成本是x元,
(1﹣15%)x=74.8
0.85x=74.8
x=88
答:原来每件产品的成本是88元。
【点评】本题主要考查了列方程解应用题,关键是根据等量关系:原来每件产品的成本×(1﹣15%)=现在每件产品的成本,列方程。
26.【分析】此题可以利用饲料总量相等建立等式,可以设王大伯一共养了x头猪,根据王大伯家的饲料总量不变,建立方程:20×(x﹣130)=15×(x+110),然后解答即可.
【解答】解:设王大伯一共养了x头猪.
20×(x﹣130)=15×(x+110)
20x﹣2600=15x+1650
5x=4250
x=850
答:王大伯一共养了850头猪.
【点评】此题属于中档题,有一定难度,利用饲料总量相等建立等式,浅显易懂,考查了学生用方程解答问题的能力.
27.【分析】设经过x分钟两人相遇,根据等量关系式:两人的速度和×相遇时间=总路程,列方程解答即可。
【解答】解:设经过x分钟两人相遇。
(72+63)x=1080
135x=1080
x=8
答:经过8分钟两人相遇。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
28.【分析】设去年同期平均每个月接待游客约x人,根据等量关系:去年同期平均每个月接待游客人数×3+200人=今年9月份以来平均每个月接待游客人数,列方程解答即可。
【解答】解:设去年同期平均每个月接待游客约x人,
3x+200=8600
3x=8400
x=2800
答:去年同期平均每个月接待游客约2800人。
【点评】本题主要考查了列方程解应用题,关键是根据等量关系:去年同期平均每个月接待游客人数×3+200人=今年9月份以来平均每个月接待游客人数,列方程。
29.【分析】如图,是正方体的展开图,属于“2﹣2﹣2”结构,把它折成正方体后,而且每个相对面上两个数的和是7(1和6,2和5,3和4),与1号面相对的6号面是第一行右边一个,与2号相对的面是中行左边一个,与3号面相对的面是上行左边一个.
【解答】解:根据分析,填数如下:
【点评】本题是考查正方体的展开图,最好的办法是让学生动手操作一下,既可以解决问题,又锻炼了学生动手操作能力.
30.【分析】首先根据题意,可得相遇时,快车多行了48×2=96(千米);然后根据路程÷时间=速度,用相遇时快车多行的路程除以相遇用的时间,求出两车的速度之差是多少,再用它加上慢车的速度,求出快车每小时行多少千米,然后用速度和乘相遇时间即可.
【解答】解:48×2÷4+60
=24+60
=84(千米)
(60+84)×4
=144×4
=576(千米)
答:两地相距576千米.
【点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握;解答此题的关键是求出两车的速度之差是多少.
31.【分析】设乙队每天开凿x米,甲队每天开凿1.25x米,先依据工作总量=工作时间×工作效率,分别求出两队开凿长度,再根据两队开凿长度和=360米列方程,依据等式的性质即可求解。
【解答】解:设乙队每天开凿x米
1.25x×4+4x=360
5x+4x=360
9x=360
x=40
40×1.25=50(米)
答:甲队每天开凿50米,乙队每天开凿40米。
【点评】解决这类问题主要找出题里面蕴含的数量关系,由此列出方程解决问题。
一.选择题
1.下面题目不能用方程4x+5=69来解决的是( )
A.合唱队有69人,比舞蹈队人数的4倍多5人,舞蹈队有x人
B.有69千克橙子,装了4箱,还剩5千克,平均每箱装x千克
C.爸爸体重69千克,再长5千克就是芳芳体重的4倍了,芳芳体重x千克
2.甲、乙两队合修一段长1400m的公路。两队同时从两头开工,5天修完。已知甲队平均每天修160m,乙队平均每天修多少米?设乙队平均每天修工xm,下列式子中正确的有( )个。
160×5+x=1400 5×(160+x) 1400÷(160+x)
1400÷5=160+x (1400﹣160×5)÷x=5 1400÷5﹣x=160
A.3 B.4 C.5 D.6
3.甲,乙两人从相距20千米的两地出发相向而行,一只小狗与甲同时出发向乙奔去,遇到乙后立即掉头向甲跑去,遇到甲后又立即掉头向乙跑去…直到甲乙两人相遇为止.已知甲的速度是6千米/小时,乙的速度是4千米/小时,小狗的速度是13千米/小时,在这一过程中,小狗共跑了( )千米.
A.18 B.20 C.24 D.26
4.如图,A、B是圆的直径的两端,小张在A点,小王在B点同时出发,相向行走,他们在距A点80米处的C点第一次相遇,接着又在距B点60米处的D点第二次相遇.那么,这个圆的周长是( )米.
A.140 B.240 C.180 D.360
5.李老师要为图书馆购置一批图书,他需要先调查( )。
A.同学们每天阅读多长时间
B.同学们在家会阅读吗
C.同学们喜欢哪几类课外书
D.同学们本学期读了几本课外书
6.如图是长方体的表面展开图,折叠成一个长方体后,那么与字母J重合的点是( )
A.H和N B.N和M C.B和H D.和N
7.下面哪个图形沿虚线对折不能围成正方体( )
A. B.
C.
8.张大爷家收了780千克苹果,装了30筐,还剩下15千克.平均每筐装x千克,下面的方程中,错误的是( )
A.780﹣30x=15 B.30x+15=780 C.30x﹣15=780
二.填空题
9.根据数量关系列出方程。(不用求解)
(1)爸爸今年x岁,小刚今年12岁,小刚比爸爸小26岁。
(2)果园里种着桃树x棵,杏树的棵数是桃树的3倍,杏树比桃树多90棵。
10.小明买了12支彩笔,每支彩笔x元,付给售货员20元,找回了2元.
+ =20元
方程: .
11.在如图中描出长度是(150+x)的一段。x= 。
12.西安大雁塔高约64米,比小雁塔高度的2倍少22米。写出等量关系式是 。
13.根据题意把方程补充完整.
甲、乙两辆汽车同时从相距270千米的两地相对开出3小时后相遇,甲车每小时行驶48千米,乙车每小时行驶多少千米?
(1)根据甲车行驶的路程+乙车行驶的路程=总路程,设乙车每小时行驶x千米,列方程: + =270
(2)根据(甲车每小时行驶的路程+乙车每小时行驶的路程)×3=总路程,设乙车每小时行驶x千米,列方程:
( + )×3=270
14.甲乙两人同时从A地走向B地,甲的速度是每分钟90米,乙的速度是每分钟80米,甲到达A地后立即返回,途中距离B地180米处与乙相遇,问乙走的路程是全程的 .
15.甲、乙两人分别从A、B两地同时出发,相向而行,他们相遇时,甲比乙多行90米,相遇后乙的速度减少50%,甲到B地后立即调头,追上乙时离A地还有90米,那么A、B两地间的距离为 米。
16.右面是一个无盖的长方体纸盒的展开图.与④号面相对的面是 号面,纸盒的底面是 号面.
17.写一写。
相对的两个面上的数字之和为7。
看到的数字是 。
18.九州旅行社有550名游客去承德避暑山庄玩,正好坐满了5辆大客车和10辆小客车.其中每辆大客车比每辆小客车多载客20人,每辆大客车能载客 人.
三.判断题
19.有两条彩带,第一条是6.9米,比第二条多出2.7米,那么第二条彩带长多少米?
解:设第二条彩带长x米,根据题意列出的方程是:6.9﹣2.7.
20.5个人种南瓜,每人种了x株,一共种了40株.
5x=40. 改正:
21.x个同学站成8行,每行有6人.
8x=6 改正:
22.用写“正”字的方法统计三月份的天气情况,一个“正”字代表一天。
23.将如图的展开图围成正方体后,与“1”相对的是“3”。
四.操作题
24.下面哪一个图形折叠起来能做成一只开口的盒子?请在图形后面打上“√”.
五.应用题
25.只列综合算式或方程,不解答。
一个工厂由于采用新工艺,现在每件产品的成本是74.8元,比原来降低了一成五。原来每件产品的成本是多少元?
26.养猪专业户王大伯说:“如果卖掉130头猪,那么饲料可维持20天;如果买进110头猪,那么饲料只能维持15天.”问:王大伯一共养了多少头猪?
27.小华和小兰同时从相距1080米的两地相向而行,小华每分钟走72米,小兰每分钟走63米,经过多少分钟两人相遇?(用方程解)
28.“半条被子”发生地汝城县沙洲村今年9月份以来平均每个月接待游客约8600人次,比去年同期的3倍还多200人。去年同期平均每个月接待游客约多少人?(用方程解)
29.正方体有6个面,每个面上分别写有1个数字,它们是1、2、3、4、5、6,而且每个相对面上两个数的和是7(1和6,2和5,3和4).如图是正方体六个面的展开图,请填出空格内的数.
30.快车和慢车同时从两地相向而行,4时后在距中点48千米处相遇.已知慢车每时行60千米,两地相距多少千米?
31.甲、乙两个工程队同时开凿一条360m长的隧道,各从一端相向施工,4天打通。甲队每天开凿的长度是乙队的1.25倍,甲、乙两队每天各开凿多少米?(用方程解答)
参考答案
一.选择题
1.【分析】A.舞蹈队人数为x人,根据等量关系:舞蹈队人数×4+5人=合唱队人数,列方程即可;
B.平均每箱装x千克,根据等量关系:平均每箱千克数×4+5千克=总千克数,列方程即可;
C.芳芳体重x千克,根据等量关系:芳芳体重×4﹣5千克=爸爸体重,列方程即可。
【解答】解:A.舞蹈队人数为x人,4x+5=69,本项不符合题意;
B.平均每箱装x千克,4x+5=69,本项不符合题意;
C.芳芳体重x千克,4x﹣5=69,本项符合题意。
故选:C。
【点评】解决这类问题主要找出题里面蕴含的数量关系,由此列出方程解决问题。
2.【分析】上面三个算式不是方程只是含有未知数的式子因此不符合方程的定义;
(4)依据甲和乙的工作效率和=甲的工作效率+乙的工作效率列方程判断;
(5)依据乙的工作量工作时间=(工作总量﹣甲的工作量)÷乙的工作量列方程判断;
(6)依据工作总量÷工作时间﹣乙的工作效率=甲的工作效率列方程判断。
【解答】解:(1)“160×5+x=1400”依据甲5天的工作总量+乙5天的工作总量=1400,但是乙只加了一天的,所以错误。
(2)“5×(160+x)”只是含有字母的式子,不能表达完整的要解决问题,解决问题没有完成。
(3)“1400÷(160+x)”是含有字母的式子,不能表达完整的要解决问题,解决问题没有完成。
(4)1400÷5=160+x,表示甲和乙的工作效率和=甲的工作效率+乙的工作效率,方程成立。
(5)(1400﹣160×5)÷x=5表示乙的工作量工作时间=(工作总量﹣甲的工作量)÷乙的工作量,方程成立。
(6)1400÷5﹣x=160表示工作总量÷工作时间﹣乙的工作效率=甲的工作效率,方程成立。
故选:A。
【点评】列方程解应用题的步骤:
①弄清题意,确定未知数,并用x表示。
②找出题中数量之间的相等关系。
③列方程,解方程。
④检查或验算,写出答案。
3.【分析】根据题意,甲、乙相遇需要的时间是20÷(6+4)=2(小时),在此过程中狗一直奔跑,所以狗跑的时间也是2小时,然后根据狗的速度,运用关系式:速度×时间=路程,解决问题.
【解答】解:20÷(6+4)×13
=2×13
=26(千米)
答:在这一过程中,小狗共跑了26千米.
故选:D.
【点评】此题解答的关键是要知道:甲、乙相遇需要的时间就是狗跑的时间.
4.【分析】两人第一次相遇时,共行了半个周长,此时小张行了80米,即每共行半个圆,小张就走80米,离开C点,第二次相遇时,两共行了3个半圆,则此时小张A从C点到D点行了80 3=240米,又B点距D点为60米,则A到B点长240﹣60=180米,所以周长是180×2=360米.
【解答】解:(80×3﹣60)×2
=(240﹣60)×2,
=180×2,
=360(米).
答:这个圆的周长是 360米.
故选:D.
【点评】根据题意得出每共行半个圆,小张就走80米是完成本题的关键.
5.【分析】李老师要为图书馆购置一批图书,首先要明确买什么种类的书,买多少书,据此解答。
【解答】解:李老师要为图书馆购置一批图书,首先要明确买什么种类的书,因此得先调查同学们的喜好。
故选:C。
【点评】解答此题的关键是理解必备的条件是什么。
6.【分析】根据长方体展开图的特征可知,与字母J重合的点是N和H。据此解答。
【解答】解:如图是长方体的表面展开图,折叠成一个长方体后,那么与字母J重合的点是N和H。
故选:A。
【点评】此题考查的目的是理解掌握长方体展开图的特征及应用。
7.【分析】根据正方体展开图的类型,1﹣4﹣1型,2﹣3﹣1型,2﹣2﹣2型,3﹣3型,据此解答即可.
【解答】解:A、B都是正方体的展开图,属于1﹣4﹣1型,能折成长方体;
C不是正方体的展开图,不能折成长方体;
故选:C.
【点评】本题是考查正方体的展开图,是培养学生的观察、分析能力和空间想象能力.此类题可动手折叠一下,即可解决问题,又锻炼了动手操作能力.
8.【分析】根据题干,设平均每筐装x千克,则可得等量关系:平均每筐装的千克数×筐数+剩下的15千克=苹果的总千克数,或者苹果的总千克数﹣平均每筐装的千克数×筐数=剩下的15千克,列出的方程是:30x+15=780或者780﹣30x=15,据此即可焦点问题.
【解答】解:设平均每筐装x千克,根据题意可得方程:
30x+15=780或者780﹣30x=15
所以上面的方程错误的是30x﹣15=780.
故选:C.
【点评】解答此题容易找出基本数量关系:平均每筐装的千克数×筐数+剩下的15千克=苹果的总千克数,或者苹果的总千克数﹣平均每筐装的千克数×筐数=剩下的15千克,由此列方程解决问题.
二.填空题
9.【分析】(1)本题的数量关系式是:爸爸的年龄﹣小刚的年龄=小刚比爸爸小的,据此我们设爸爸今年x岁,列出的方程就是:x﹣12=26;
(2)根据题意我们知道:杏树的棵数×3=桃树的棵数,如果桃树有x
棵,那么杏树的棵数就用3x来表示,还知道杏树的棵数﹣桃树的棵数=90,据此列出的方程就是:3x﹣x=90。
【解答】解:(1)爸爸今年x岁,小刚今年12岁,小刚比爸爸小26岁。
x﹣12=26
(2)果园里种着桃树x棵,杏树的棵数是桃树的3倍,杏树比桃树多90棵。
3x﹣x=90
故答案为:(1)x﹣12=26;(2)3x﹣x=90。
【点评】观察题干,分析数量关系,设出未知数列方程即可。
10.【分析】设每支彩笔x元,则根据等量关系:彩笔的价格×12+找回的2元=付出的钱数20元,据此列出方程解决问题.
【解答】解:设每支彩笔x元,则根据等量关系:彩笔的价格×12+找回的2元=付出的钱数20元,据此列出方程是:
12x+2=20
12x=18
x=1.5
答:每支彩笔1.5元.
故答案为:彩笔的价格×12;找回的2元;12x+2=20.
【点评】解答此题容易找出基本数量关系,由此列方程解决问题.
11.【分析】根据图意,图中(150+x)的一段是200米,可以列出方程:150+x=200,求出方程的解即可。
【解答】解:150+x=200
150+x﹣150=200﹣150
x=50
故答案为:50。
【点评】本题考查列方程求解的问题,解题关键是找出题目中的等量关系列方程解答。
12.【分析】根据题意可知,小雁塔的高×2﹣22米=大雁塔的高64米,据此解答即可。
【解答】解:等量关系式是:小雁塔的高×2﹣22米=大雁塔的高64米。
故答案为:小雁塔的高×2﹣22米=大雁塔的高64米。
【点评】解答此题,首先弄清题意,分清已知与所求,再找出基本的等量关系。
13.【分析】(1)根据题干,设乙车每小时行驶x千米,根据等量关系:甲车行驶的路程+乙车行驶的路程=总路程,列出方程为:48×3+3x=270,据此即可解答问题;
(2)根据题干,设乙车每小时行驶x千米,根据等量关系:(甲车每小时行驶的路程+乙车每小时行驶的路程)×3=总路程,列出方程为:(48+x)×3=270,解除即可解答问题.
【解答】解:(1)设乙车每小时行驶x千米,根据题意可得:
48×3+3x=270
144+3x=270
3x=126
x=42
答:乙车每小时行驶42千米.
(2)设乙车每小时行驶x千米,根据题意可得:
(48+x)×3=270
48+x=90
x=42
答:乙车每小时行驶42千米.
【点评】此题主要考查相遇问题中的基本数量关系:甲车所行的路程+乙车所行的路程=两地之间的距离或速度和×相遇时间=总路程;再由关系式列方程解决问题.
14.【分析】根据题意可知:甲比乙多行180×2=360(米),利用追及问题公式:追及时间=路程差÷速度差,把数代入计算得:360÷(90﹣80)=36(分钟);然后利用公式:路程=速度×时间,求乙所行路程及全程,即可求解.
【解答】解:180×2÷(90﹣80)×80
=360÷10×80
=36×80
=32880(米)
2880÷(2880+180)
=2880÷3060
≈94%
答:乙走的路程是全程的 94%.
故答案为:94%.
【点评】本题主要考查相遇问题,关键利用路程、速度和时间的关系做题.
15.【分析】画出线段图,设A,B两地的距离为2a米,相遇时甲比乙多行90米,也就是甲走了(a+45)米,乙走了(a﹣45)米,他们的速度比为(a+45):(a﹣45),乙降速后两人的速度比变为(a+45):=2(a+45):(a﹣45),追及时,甲走的路程为a﹣45+2a﹣90=3a﹣135(米),乙走的路程为a+45﹣90=a﹣45(米),根据追及时,路程比等于速度比,列出方程求解即可。
【解答】解:线段图:
设A,B两地的距离为2a米,
相遇时甲比乙多行90米,
也就是甲走了(a+45)米,乙走了(a﹣45)米,
他们的速度比为(a+45):(a﹣45),
乙降速后两人的速度比变为(a+45):=2(a+45):(a﹣45),
追及时,甲走的路程为a﹣45+2a﹣90=3a﹣135(米),乙走的路程为a+45﹣90=a﹣45(米),
根据追及时,路程比等于速度比,
=
3a﹣135=2a+90
a=225
2a=450
答:A、B两地间的距离为450米。
故答案为:450。
【点评】本题主要考查了相遇与追及问题的综合,把握相遇问题和追及问题中,路程比等于速度比,是本题解题的关键。
16.【分析】根据长方体的特征,长方体6个面都是长方形(特殊情况有两个相对的面是正方形),相对面的面积相对。通过观察这个长方体的展开图可知,与④号面相对的面①
号,③号面与⑤号面相对,由此可知,这个纸盒的底面是②号面。据此解答。
【解答】解:通过观察长方体的展开图可知,与④号面相对的面①号,③号面与⑤号面相对,所以这个纸盒的底面是②号面。
答:这个无盖纸盒的底面是②号面。
故答案为:①、②。
【点评】此题考查的目的是理解掌握长方体展开图的特征及应用。
17.【分析】根据题意和图示可知,相对的两个面上的数字之和为7,那么图中的已知的数字5的对面就是2,6的对面的数字是1,4的对面的数是3,看看图中小男孩站的位置,据此解答。
【解答】解:小男站的位置是正方体的左面,根据正方体右边的数字是6,可以推出7﹣6=1,因此小男孩看到是数字是1。
故答案为:1。
【点评】解答此题的关键理解相对的面的意思。
18.【分析】根据题意可知,5辆大客车载客的人数+10辆小客车载客的人数=550人,已知每辆大客车比每辆小客车多载客20人,设每辆大客车能载客x人,则每辆小客车能载(x﹣20)人,据此列方程解答.
【解答】解:设每辆大客车能载客x人,则每辆小客车能载(x﹣20)人,
5x+(x﹣20)×10=550
5x+10x﹣200=550
15x﹣200=550
15x﹣200+200=550+200
15x=750
15x÷15=750÷15
x=50
答:每辆大客车能载客50人.
故答案为:50.
【点评】解决这类问题主要找出题里面蕴含的等量关系,设出未知数,由此列出方程解决问题.
三.判断题
19.【分析】根据题意可知,第二条的长度+2.7米=第一条的长度(9.6米),或第二条的长度=第一条的长度(9.6米)减去2.7米。设第二条彩带长为x米,据此可方程:x+2.7=9.6,或x=9.6﹣2.7。据此判断。
【解答】解:设第二条彩带长为x米,据此可方程:x+2.7=9.6。
所以原题的说法错误。
故答案为:×。
【点评】此题考查的目的理解掌握方程的意义及应用,明确:含有未知数的等式叫做方程。
20.【分析】根据题意,分析数量关系,可得等量关系式:每人种的株数×人数=总株数,然后设每人种了x株,再列方程解答即可.
【解答】解:设每人种了x株,
5x=40
5x÷5=40÷5
x=8
答:每人种了8株.
故答案为:√,﹣﹣﹣﹣.
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题.
21.【分析】根据题意,分析数量关系,可得等量关系式:每行的人数=总人数÷行数,然后设有x个同学,再列方程解答即可.
【解答】解:设有x个同学,
x÷8=6
x=8×6
x=48
答:有48个同学.
故答案为:×,x÷8=6.
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题.
22.【分析】正”有5笔,每一笔表示1个统计量,由此判断。
【解答】解:用写“正”字的方法统计三月份的天气情况,一个“正”字代表5天;
原题说法错误。
故答案为:×。
【点评】本题考查了用“正”字表示统计量的方法,一个“正”字表示5。
23.【分析】根据正方体展开图的11种特征,此图属于正方体展开图的“1﹣4﹣1”型,折成正方体后,“1”与“3”相对,“2”与“4”相对,“5”与“6”相对。
【解答】解:如图
围成正方体后,与“1”相对的是“3”。
原题说法正确。
故答案为:√。
【点评】正方体展开图分四种类型,11种情况,每种情况折成正方体后哪些面相对是有规律的,可自己动手操作一下并记住,能快速解答此类题。
四.操作题
24.【分析】a、b、f属于正方体展开图的“1﹣4﹣1”型,去掉一个“1”,能做成一只开口的盒子;c、d在任何添上一个正方形都不是正方体展开图,不能做成一只开口的盒子;e属于正方形展开图的“1﹣3﹣2”型,去掉“3”中的一个正方开,能做成一只开口的盒子.
【解答】解:下面哪一个图形折叠起来能做成一只开口的盒子?请在图形后面打上“√”.
【点评】关键记住正方体展开图的11种情况:正方体展开图分四种类型,即:第一种:“1﹣4﹣1”结构,即第一行放1个,第二行放4个,第三行放1个;第二种:“2﹣2﹣
2”结构,即每一行放2个正方形,此种结构只有一种展开图;第三种:“3﹣3”结构,即每一行放3个正方形,只有一种展开图;第四种:“1﹣3﹣2”结构,即第一行放1个正方形,第二行放3个正方形,第三行放2个正方形.
五.应用题
25.【分析】降低一成五就是指比原来降低了15%,设原来每件产品的成本是x元,根据等量关系:原来每件产品的成本×(1﹣15%)=现在每件产品的成本,列方程解答即可。
【解答】解:设原来每件产品的成本是x元,
(1﹣15%)x=74.8
0.85x=74.8
x=88
答:原来每件产品的成本是88元。
【点评】本题主要考查了列方程解应用题,关键是根据等量关系:原来每件产品的成本×(1﹣15%)=现在每件产品的成本,列方程。
26.【分析】此题可以利用饲料总量相等建立等式,可以设王大伯一共养了x头猪,根据王大伯家的饲料总量不变,建立方程:20×(x﹣130)=15×(x+110),然后解答即可.
【解答】解:设王大伯一共养了x头猪.
20×(x﹣130)=15×(x+110)
20x﹣2600=15x+1650
5x=4250
x=850
答:王大伯一共养了850头猪.
【点评】此题属于中档题,有一定难度,利用饲料总量相等建立等式,浅显易懂,考查了学生用方程解答问题的能力.
27.【分析】设经过x分钟两人相遇,根据等量关系式:两人的速度和×相遇时间=总路程,列方程解答即可。
【解答】解:设经过x分钟两人相遇。
(72+63)x=1080
135x=1080
x=8
答:经过8分钟两人相遇。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
28.【分析】设去年同期平均每个月接待游客约x人,根据等量关系:去年同期平均每个月接待游客人数×3+200人=今年9月份以来平均每个月接待游客人数,列方程解答即可。
【解答】解:设去年同期平均每个月接待游客约x人,
3x+200=8600
3x=8400
x=2800
答:去年同期平均每个月接待游客约2800人。
【点评】本题主要考查了列方程解应用题,关键是根据等量关系:去年同期平均每个月接待游客人数×3+200人=今年9月份以来平均每个月接待游客人数,列方程。
29.【分析】如图,是正方体的展开图,属于“2﹣2﹣2”结构,把它折成正方体后,而且每个相对面上两个数的和是7(1和6,2和5,3和4),与1号面相对的6号面是第一行右边一个,与2号相对的面是中行左边一个,与3号面相对的面是上行左边一个.
【解答】解:根据分析,填数如下:
【点评】本题是考查正方体的展开图,最好的办法是让学生动手操作一下,既可以解决问题,又锻炼了学生动手操作能力.
30.【分析】首先根据题意,可得相遇时,快车多行了48×2=96(千米);然后根据路程÷时间=速度,用相遇时快车多行的路程除以相遇用的时间,求出两车的速度之差是多少,再用它加上慢车的速度,求出快车每小时行多少千米,然后用速度和乘相遇时间即可.
【解答】解:48×2÷4+60
=24+60
=84(千米)
(60+84)×4
=144×4
=576(千米)
答:两地相距576千米.
【点评】此题主要考查了行程问题中速度、时间和路程的关系:速度×时间=路程,路程÷时间=速度,路程÷速度=时间,要熟练掌握;解答此题的关键是求出两车的速度之差是多少.
31.【分析】设乙队每天开凿x米,甲队每天开凿1.25x米,先依据工作总量=工作时间×工作效率,分别求出两队开凿长度,再根据两队开凿长度和=360米列方程,依据等式的性质即可求解。
【解答】解:设乙队每天开凿x米
1.25x×4+4x=360
5x+4x=360
9x=360
x=40
40×1.25=50(米)
答:甲队每天开凿50米,乙队每天开凿40米。
【点评】解决这类问题主要找出题里面蕴含的数量关系,由此列出方程解决问题。
