6.2.1向量的加法运算 6.2.2 向量的减法运算(共18张PPT)
文档属性
| 名称 | 6.2.1向量的加法运算 6.2.2 向量的减法运算(共18张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 439.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 08:45:16 | ||
图片预览






文档简介
(共18张PPT)
6.2 平面向量的运算
6.2.1 向量的加法运算
6.2.2 向量的减法运算
1.借助实例和平面向量的几何表示,掌握平面向量加、减运算及运算规则,理解其几何意义.
2.理解向量减法与加法的关系,并能正确作出两个向量的差向量.
向量的加法
三角形 法则 加法定义 求① 两个向量 和的运算,叫做向量的加法.两个向量的和仍是一个向量
符号表示 若 =a, =b,则a+b= + =②
文字语言 已知非零向量a,b,在平面内取③ 任意 一点A,作 =a, =b,则向量 叫做a与b的和,记作④ a+b
图形表示
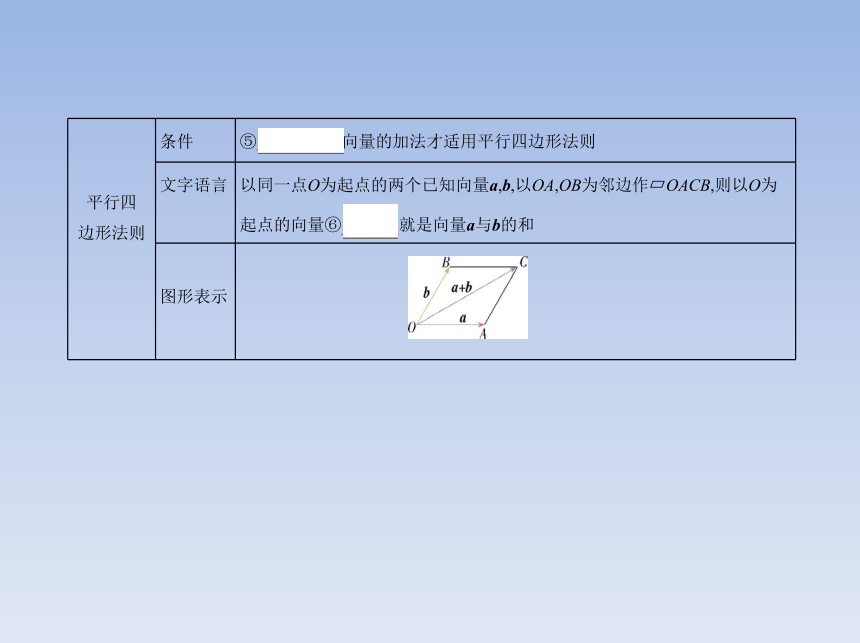
平行四 边形法则 条件 ⑤ 不共线 向量的加法才适用平行四边形法则
文字语言 以同一点O为起点的两个已知向量a,b,以OA,OB为邻边作 OACB,则以O为起点的向量⑥ 就是向量a与b的和
图形表示
向量的有关性质
1.一般地,我们有|a+b|≤|a|+|b|,当且仅当a,b方向相同时等号成立.
2.在△ABC中, + + =0.
3.向量加法的运算律
(1)交换律:a+b=⑦ b+a ,对于零向量与任意向量a,我们规定a+0=0+a=a.
(2)结合律:a+(⑧ b+c )=(a+b)+c.
向量的减法
相反向量 与向量a长度相等,方向⑨ 相反 的向量,叫做a的相反向量,记作-a.零向量的相反向量仍是零向量
向量减法的 几何意义 已知向量a,b,在平面内任取一点O,作 =a, =b,则 =⑩ a-b .
a-b可以表示为从向量b的终点指向向量a的终点的向量
1.两个向量的和可能是数量. ( )
2.两个向量相加就是它们的模相加. ( )
判断正误,正确的画“√” ,错误的画“ ” .
提示:因为向量既有大小,又有方向,所以两个向量相加不是模的相加.两个向量相加满足三角形法则或平行四边形法则.
3. + = . ( √ )
4. = - . ( √ )
5. + + + + + =0. ( )
6.两个同向向量的差一定小于这两个向量的和. ( )
7.向量加法的平行四边形法则适合任意两个向量. ( )
平面向量的加、减法运算及应用
在水流速度大小为4 km/h的河中,如果船以大小为12 km/h的实际航速垂直于河岸行驶,求船航行速度的大小和方向.
1.画出题目中的示意图并求解.
提示:如图,设 表示水流速度, 表示船实际的航行速度,则 表示船航行的速度.
由题意知,| |=4 ,| |=12,∠CAB=90°,所以tan∠ACB= = ,所以∠ACB=30°,∠CAD=30°.所以| |=8 ,∠BAD=120°,即船航行速度的大小为8 km/h,方向与水流方向所成角为120°.
2.问题1中用的是什么方法
提示:向量加法的平行四边形法则.
1.在使用向量加法的三角形法则时,要注意“首尾相接”,即第一个向量的终点与第二个向量的起点重合,则以第一个向量的起点为起点,并以第二个向量的终
点为终点的向量为两向量的和;向量加法的平行四边形法则的应用前提是“共起点”,即两个向量是从同一点出发的不共线向量.
2.已知n个向量,把这n个向量首尾顺次相连,以第一个向量的起点为起点,第n个
向量的终点为终点的向量叫做这n个向量的和向量,这个法则叫做向量求和的多边形法则.当首尾顺次相连的若干个向量构成封闭的向量链时,各个向量的和为0.
如图所示,在n边形A1A2…An中,有 + +…+ = ,则 +
+…+ + =0.
3.向量减法的三角形法则中,强调了差向量的“箭头”指向被减向量,可简记为“共起点,连终点,指被减”.
思路点拨
利用向量加、减法的法则作图求解.
已知|a|=8,|b|=6,且|a+b|=|a-b|,求|a-b|.
解析 设 =a, =b,以AB,AD为邻边作平行四边形ABCD,如图所示,
则 =a+b, =a-b.
因为|a+b|=|a-b|,所以| |=| |.
又因为四边形ABCD为平行四边形,
所以四边形ABCD为矩形,故AD⊥AB.
在Rt△DAB中,| |=|a|=8,| |=|b|=6,由勾股定理,得| |= =
=10,所以|a-b|=10.
向量形式的三角形不等式
(1)当向量a,b不共线时,作 =a, =b,则a+b= ,如图1所示.根据三角形的三
边关系,有||a|-|b||<|a+b|<|a|+|b|.
(2)当a与b同向共线或a,b中至少有一个为零向量时,作法同(1),如图2所示,此时
|a+b|=|a|+|b|.
(3)当a与b反向共线或a,b中至少有一个为零向量时,不妨设|a|≥|b|,作法同(1),如图3所示,此时|a+b|=|a|-|b|.
故对于任意向量a,b,总有||a|-|b||≤|a+b|≤|a|+|b|①.
由于|a-b|=|a+(-b)|,
所以||a|-|-b||≤|a-b|<|a|+|-b|,
即||a|-|b||≤|a-b|≤|a|+|b|②.
将①②两式结合,可得||a|-|b||≤|a±b|≤|a|+|b|,我们称之为向量形式的三角形不等式.
给出下列关系式:
①|a|-|b|<|a+b|<|a|+|b|;
②|a|-|b|=|a+b|=|a|+|b|;
③|a|-|b|=|a+b|<|a|+|b|;
④|a|-|b|<|a+b|=|a|+|b|.
其中,一定不成立的关系式的个数是 ( A )
A.0 B.1 C.2 D.3
思路点拨
从a,b是不是共线向量或零向量进行分析、判断.
解析 ①当a与b不共线时成立;②当b=0时成立;③当a与b共线,且方向相反,|a|≥|b|时成立;④当a与b共线,且方向相同时成立.故一定不成立的关系式的个数是0.
答案 A
设|a|=8,|b|=12,则|a+b|的最大值与最小值分别为 20,4 .
思路点拨
利用向量形式的三角形不等式求解.
解析 当a,b共线且同向时,|a+b|=|a|+|b|=8+12=20;
当a,b共线且反向时,|a+b|=||a|-|b||=4;
当a,b不共线时,||a|-|b||<|a+b|<|a|+|b|,即4<|a+b|<20.
所以|a+b|的最大值为20,最小值为4.
答案 20,4
6.2 平面向量的运算
6.2.1 向量的加法运算
6.2.2 向量的减法运算
1.借助实例和平面向量的几何表示,掌握平面向量加、减运算及运算规则,理解其几何意义.
2.理解向量减法与加法的关系,并能正确作出两个向量的差向量.
向量的加法
三角形 法则 加法定义 求① 两个向量 和的运算,叫做向量的加法.两个向量的和仍是一个向量
符号表示 若 =a, =b,则a+b= + =②
文字语言 已知非零向量a,b,在平面内取③ 任意 一点A,作 =a, =b,则向量 叫做a与b的和,记作④ a+b
图形表示
平行四 边形法则 条件 ⑤ 不共线 向量的加法才适用平行四边形法则
文字语言 以同一点O为起点的两个已知向量a,b,以OA,OB为邻边作 OACB,则以O为起点的向量⑥ 就是向量a与b的和
图形表示
向量的有关性质
1.一般地,我们有|a+b|≤|a|+|b|,当且仅当a,b方向相同时等号成立.
2.在△ABC中, + + =0.
3.向量加法的运算律
(1)交换律:a+b=⑦ b+a ,对于零向量与任意向量a,我们规定a+0=0+a=a.
(2)结合律:a+(⑧ b+c )=(a+b)+c.
向量的减法
相反向量 与向量a长度相等,方向⑨ 相反 的向量,叫做a的相反向量,记作-a.零向量的相反向量仍是零向量
向量减法的 几何意义 已知向量a,b,在平面内任取一点O,作 =a, =b,则 =⑩ a-b .
a-b可以表示为从向量b的终点指向向量a的终点的向量
1.两个向量的和可能是数量. ( )
2.两个向量相加就是它们的模相加. ( )
判断正误,正确的画“√” ,错误的画“ ” .
提示:因为向量既有大小,又有方向,所以两个向量相加不是模的相加.两个向量相加满足三角形法则或平行四边形法则.
3. + = . ( √ )
4. = - . ( √ )
5. + + + + + =0. ( )
6.两个同向向量的差一定小于这两个向量的和. ( )
7.向量加法的平行四边形法则适合任意两个向量. ( )
平面向量的加、减法运算及应用
在水流速度大小为4 km/h的河中,如果船以大小为12 km/h的实际航速垂直于河岸行驶,求船航行速度的大小和方向.
1.画出题目中的示意图并求解.
提示:如图,设 表示水流速度, 表示船实际的航行速度,则 表示船航行的速度.
由题意知,| |=4 ,| |=12,∠CAB=90°,所以tan∠ACB= = ,所以∠ACB=30°,∠CAD=30°.所以| |=8 ,∠BAD=120°,即船航行速度的大小为8 km/h,方向与水流方向所成角为120°.
2.问题1中用的是什么方法
提示:向量加法的平行四边形法则.
1.在使用向量加法的三角形法则时,要注意“首尾相接”,即第一个向量的终点与第二个向量的起点重合,则以第一个向量的起点为起点,并以第二个向量的终
点为终点的向量为两向量的和;向量加法的平行四边形法则的应用前提是“共起点”,即两个向量是从同一点出发的不共线向量.
2.已知n个向量,把这n个向量首尾顺次相连,以第一个向量的起点为起点,第n个
向量的终点为终点的向量叫做这n个向量的和向量,这个法则叫做向量求和的多边形法则.当首尾顺次相连的若干个向量构成封闭的向量链时,各个向量的和为0.
如图所示,在n边形A1A2…An中,有 + +…+ = ,则 +
+…+ + =0.
3.向量减法的三角形法则中,强调了差向量的“箭头”指向被减向量,可简记为“共起点,连终点,指被减”.
思路点拨
利用向量加、减法的法则作图求解.
已知|a|=8,|b|=6,且|a+b|=|a-b|,求|a-b|.
解析 设 =a, =b,以AB,AD为邻边作平行四边形ABCD,如图所示,
则 =a+b, =a-b.
因为|a+b|=|a-b|,所以| |=| |.
又因为四边形ABCD为平行四边形,
所以四边形ABCD为矩形,故AD⊥AB.
在Rt△DAB中,| |=|a|=8,| |=|b|=6,由勾股定理,得| |= =
=10,所以|a-b|=10.
向量形式的三角形不等式
(1)当向量a,b不共线时,作 =a, =b,则a+b= ,如图1所示.根据三角形的三
边关系,有||a|-|b||<|a+b|<|a|+|b|.
(2)当a与b同向共线或a,b中至少有一个为零向量时,作法同(1),如图2所示,此时
|a+b|=|a|+|b|.
(3)当a与b反向共线或a,b中至少有一个为零向量时,不妨设|a|≥|b|,作法同(1),如图3所示,此时|a+b|=|a|-|b|.
故对于任意向量a,b,总有||a|-|b||≤|a+b|≤|a|+|b|①.
由于|a-b|=|a+(-b)|,
所以||a|-|-b||≤|a-b|<|a|+|-b|,
即||a|-|b||≤|a-b|≤|a|+|b|②.
将①②两式结合,可得||a|-|b||≤|a±b|≤|a|+|b|,我们称之为向量形式的三角形不等式.
给出下列关系式:
①|a|-|b|<|a+b|<|a|+|b|;
②|a|-|b|=|a+b|=|a|+|b|;
③|a|-|b|=|a+b|<|a|+|b|;
④|a|-|b|<|a+b|=|a|+|b|.
其中,一定不成立的关系式的个数是 ( A )
A.0 B.1 C.2 D.3
思路点拨
从a,b是不是共线向量或零向量进行分析、判断.
解析 ①当a与b不共线时成立;②当b=0时成立;③当a与b共线,且方向相反,|a|≥|b|时成立;④当a与b共线,且方向相同时成立.故一定不成立的关系式的个数是0.
答案 A
设|a|=8,|b|=12,则|a+b|的最大值与最小值分别为 20,4 .
思路点拨
利用向量形式的三角形不等式求解.
解析 当a,b共线且同向时,|a+b|=|a|+|b|=8+12=20;
当a,b共线且反向时,|a+b|=||a|-|b||=4;
当a,b不共线时,||a|-|b||<|a+b|<|a|+|b|,即4<|a+b|<20.
所以|a+b|的最大值为20,最小值为4.
答案 20,4
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
