沪科版数学八年级下册20.1数据的频数分布(第二课时频数分布直方图综合)课件(共31张PPT)
文档属性
| 名称 | 沪科版数学八年级下册20.1数据的频数分布(第二课时频数分布直方图综合)课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 921.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 16:43:14 | ||
图片预览






文档简介
(共31张PPT)
20.1 数据的频数分布
第20章 数据的初步分析
沪科版数学八年级下册
第二课时
1.根据具体的问题,学生会选择用直方图描述数据,会确定合适的组距和组数,会准确的画频数分布直方图。
3.培养在实际生活中的统计意识,感受统计知识的应用价值
2、进一步经历数据的整理和表示的过程,能利用简单的频数分布直方图解释数据中蕴含的信息,对实际问题作出判断和决策,初步建立统计概念
教学目标
(1)求极差,即数据中最大值与最小值的差.
(2)决定组距与组数 :组距=极差/组数.
(3) 决定分点:
登记频数,计算频率,列出频率分布表.
画一组数据的频率分布直方图,可以按以下的步骤进行:
(5)画出频率分布直方图.(纵轴表示频率/组距)
知识回顾
计算最大值和最小值的差,可以知道这组数据的变动范围.
(4) 列出频数分布表;
组距:把所有数据分组,每个小组的两个端点之间的距离(组内数据的取值范围)称为组距.
每一小组的频数与数据总数的比值
频率
每一小组数据的出现次数
频数
注意:
1、组距和组数没有确定标准,当数据在 1000个以内时,通常分成5~12组;
知识回顾
2、频数分布直方图中长方形的面积表示数据落在各个小组内的频数
3、在等距离分组中,由于小长方形的面积与高的比是常数(组距),所以在作频数分布直方图时,用小长方形的高表示频数。
1.对某校八(1)班50名学生的年龄进行调查,其中15岁的有2人,14岁的有45人,13岁的有3人,则14岁的频数为_____,频率为 ____。
2.一组数据中共有40个数,其中23出现的频率为0.3,则这40个数中,23出现的频数为____ 。
3.把50个数据分成六组,其中有一组的频数是14,有两组的频数是10,有两组的频率是0.14,则另一组的频数是____ ,频率是____。
知识回顾
45
练一练
0.9
12
0.18
9
39.5
49.5
59.5
69.5
79.5
89.5
99.5
成绩/分
学生人数
5
10
15
20
6
8
10
18
16
2
知识回顾
练一练
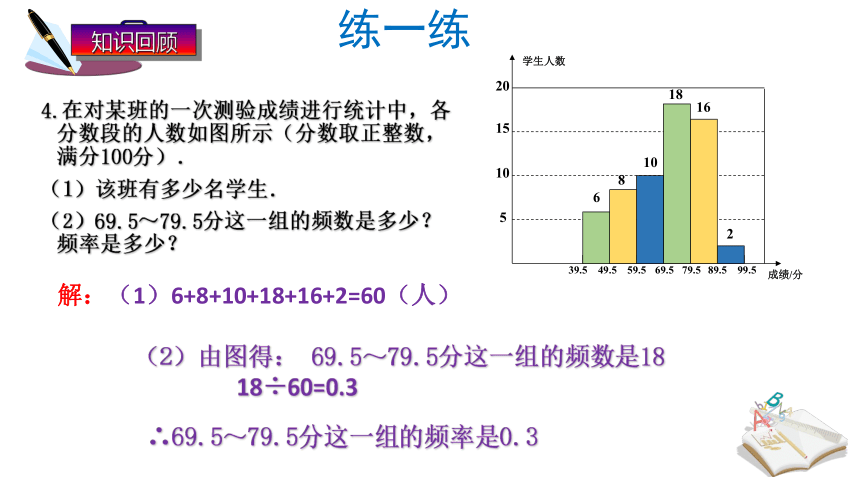
4.在对某班的一次测验成绩进行统计中,各分数段的人数如图所示(分数取正整数,满分100分).
(1)该班有多少名学生.
(2)69.5~79.5分这一组的频数是多少?频率是多少?
解:(1)6+8+10+18+16+2=60(人)
(2)由图得: 69.5~79.5分这一组的频数是18
18÷60=0.3
∴69.5~79.5分这一组的频率是0.3
学号 性别 身高 (厘米) 入学成绩
语 数 英
1 女 167 81 88 优
2 男 162 78 85 良
3 女 165 86 90 优
4 男 160 81 99 中
5 女 165 94 86 优
6 女 167 83 75 良
7 女 165 88 94 优
8 男 166 79 98 优
9 女 159 72 65 中
10 男 169 86 97 优
11 男 168 91 96 优
12 男 158 80 93 良
13 男 160 85 89 优
14 女 159 90 84 优
15 女 162 91 89 优
学号 性别 身高 (厘米) 入学成绩
语 数 英
16 女 162 83 85 优
17 女 157 86 80 优
18 女 160 92 93 优
19 男 164 83 89 优
20 女 161 75 77 良
21 男 162 86 97 优
22 男 164 91 91 优
23 女 163 87 82 优
24 男 154 82 88 优
25 男 172 68 70 中
26 男 153 88 95 优
27 男 156 80 87 优
28 男 163 82 81 优
29 男 164 78 75 良
30 女 161 89 87 优
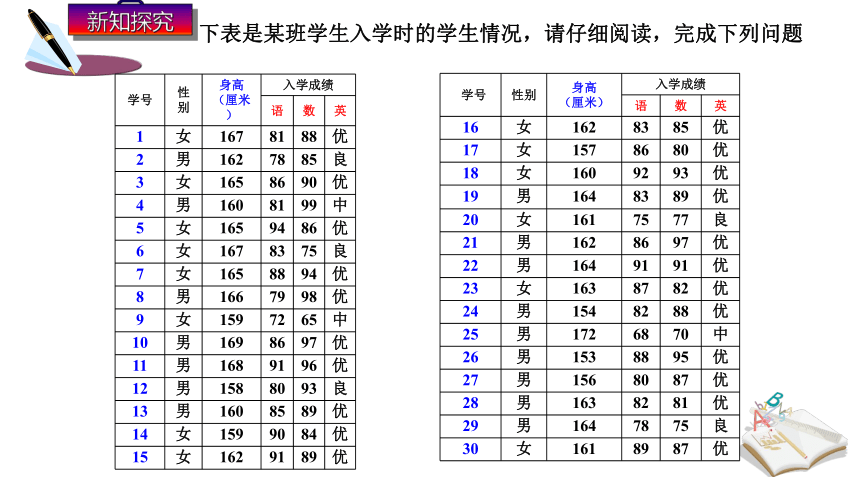
新知探究
下表是某班学生入学时的学生情况,请仔细阅读,完成下列问题
学号 入学成绩
英
1 优
2 良
3 优
4 中
5 优
6 良
7 优
8 优
9 中
10 优
11 优
12 良
13 优
14 优
15 优
学号 入学成绩
英
16 优
17 优
18 优
19 优
20 良
21 优
22 优
23 优
24 优
25 中
26 优
27 优
28 优
29 良
30 优
新知探究
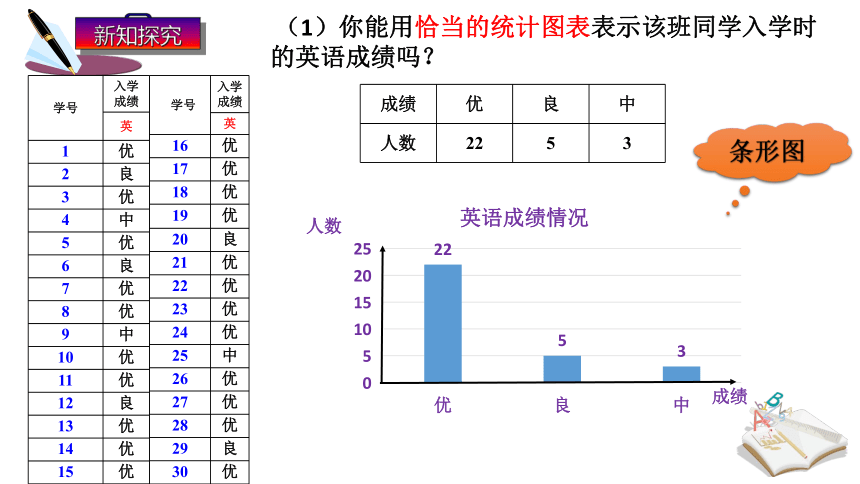
(1)你能用恰当的统计图表表示该班同学入学时的英语成绩吗?
成绩 优 良 中
人数 22 5 3
条形图
从你的图表中能看出大部分同学英语成绩处于哪个等级?
成绩 优 良 中
人数 22 5 3
整体成绩优秀偏多
英语成绩的整体分布情况怎样?
优
新知探究
(2)你能用恰当的统计图表表示该班同学入学时的语文成绩吗?从你的图表中能看出大部分同学处于哪个分数段?成绩的整体分布情况怎样?
成绩 68分 72分 75分 78分 79分 80分 81分 82分 83分
人数 1 1 1 2 1 2 2 2 3
成绩 85分 86分 87分 88分 89分 90分 91分 92分 94分
人数 1 4 1 2 1 1 3 1 1
新知探究
条形图
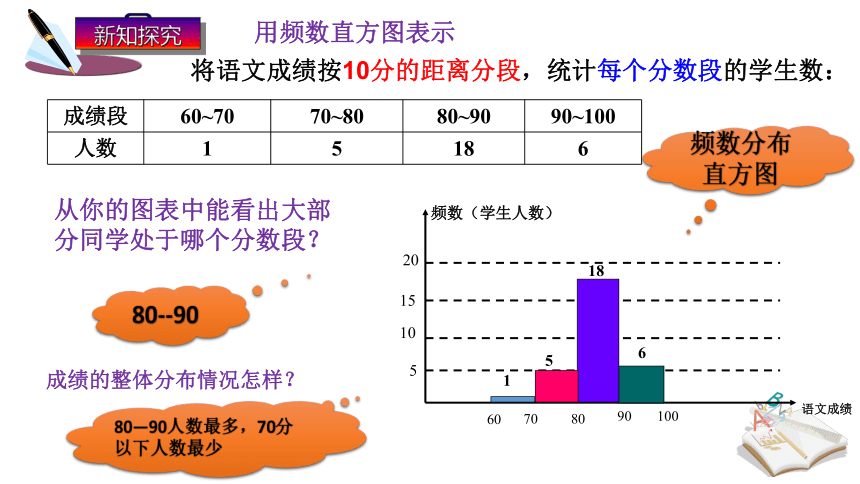
将语文成绩按10分的距离分段,统计每个分数段的学生数:
成绩段 60~70 70~80 80~90 90~100
人数 1 5 18 6
新知探究
用频数直方图表示
5
10
15
20
60
70
80
90
100
语文成绩
频数(学生人数)
1
5
18
6
从你的图表中能看出大部分同学处于哪个分数段?
频数分布直方图
成绩的整体分布情况怎样?
80--90
80—90人数最多,70分以下人数最少
如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、更直观地反映数据的整体状况.
5
10
15
20
60
70
80
90
100
语文成绩
频数(学生人数)
新知探究
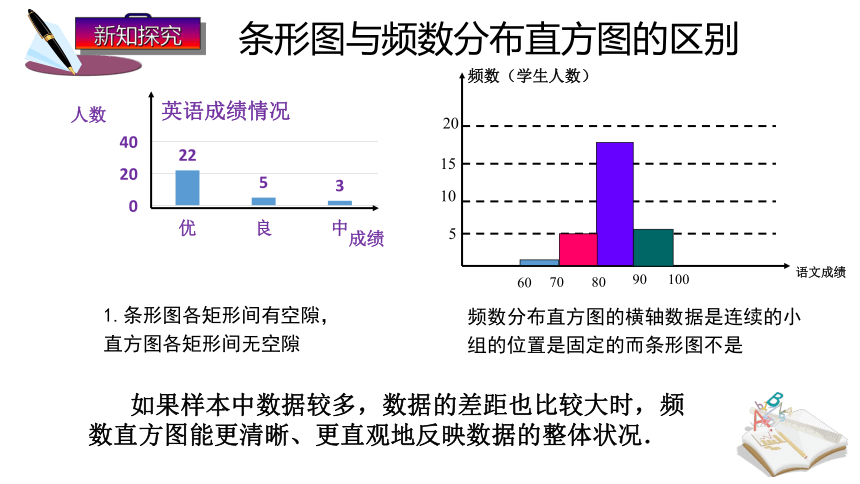
1.条形图各矩形间有空隙,直方图各矩形间无空隙
频数分布直方图的横轴数据是连续的小组的位置是固定的而条形图不是
条形图与频数分布直方图的区别
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况.
新知讲解
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
例1 为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm):
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
例题讲解
解:(1)计算最大值和最小值的差
在样本数据中,最大值是7.4,最小值是4.0,它们的差是
7.4-4.0=3.4
(2)决定组距和组数
最大值与最小值的差是3.4 ,若取组距为0.3 ,那么由于
可以分成12组,组数合适,于是取组距为0.3 ,组数为 12.
例题讲解
例题讲解
(3)确定分点
4.0≤x<4.3
4.3≤x<4.6
4.6≤x<4.9
4.9≤x<5.2
5.2≤x<5.5
5.5≤x<5.8
5.8≤x<6.1
6.1≤x<6.4
6.4≤x<6.7
6.7≤x<7.0
7.0≤x<7.3
7.3≤x<7.6
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
组距为0.3
最小值
例题讲解
(3)列频数分布表
分 组 划 记 频 数
4.0≤x<4.3
4.3≤x<4.6
4.6≤x<4.9
4.9≤x<5.2
5.2≤x<5.5
5.5≤x<5.8
5.8≤x<6.1
6.1≤x<6.4
6.4≤x<6.7
6.7≤x<7.0
7.0≤x<7.3
7.3≤x<7.6
合 计
一
一
丅
正
正正一
正正正
正正正正正
正正
正正一
正正
丅
一
1
1
2
5
11
15
28
13
11
10
2
1
100
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
4.0
6.1
5.5
5.2
4.9
4.6
4.3
6.4
5.8
6.7
7.0
7.3
7.6
(4)画频数分布直方图
例题讲解
(4)画频数分布直方图
例题讲解
4.0
从表和图中可以看出,麦穗长度大部分落在5.2 cm至7.0 cm之间,其他区域较少.长度在5.8≤x<6.1范围内的麦穗个数最多,有28个,而长度在4.0≤x<4.3,4.3≤x<4.6, 4.6≤x<4.9, 7.0≤x<7.3, 7.3≤x<7.6 范围内的麦穗个数很少,总共有7个.
例2 下图是某班同学体育课体适能测验—屈膝仰卧起坐的次数分配直方图,请依图回答下列问题:
(1)哪一组次数的人最多?
(2)全班有多少人屈膝仰卧起坐的次数在40次以上(含 40 次)?
(3)全班有多少人屈膝仰卧起坐的次数不到 30 次?
例题讲解
(1)次数为 30~35 的这组人数最多,有10人.
(2)40~45 及 45~50 这两组都是 40 次以上,共有 6+6=12 (人).
(3)20~25 及 25~30 这两组都不到 30 次,共有 6+7=13 (人).
解:
费尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,主要授予年轻的数学家,美籍华人丘成桐(1949年出生)1982年获得费尔兹奖.
1、下列数据是截至到今年费尔兹奖得主获奖时的年龄.
29 39 35 33 39 28 33 35
31 31 37 32 38 36 31 39
32 38 37 34 29 34 38 32
35 36 33 29 32 35 36 37
39 38 40 38 37 39 38 34
33 40 36 36 37 40 31 38
拓展练习
请根据下面不同分组列出频数分布表,画出频数分布直方图,比较哪一种分组能更好地说明费尔兹奖得主获奖时的年龄分布:
组距是2:
各组是28 ≤ x< 30 , 30≤ x < 32 ,...
2. 组距是5,
各组是25 ≤ x< 30 , 30≤ x < 35 ,...
3. 组距是10,
各组是20 ≤ x< 30 , 30≤ x < 40 ,...
29 39 35 33 39 28 33 35
31 31 37 32 38 36 31 39
32 38 37 34 29 34 38 32
35 36 33 29 32 35 36 37
39 38 40 38 37 39 38 34
33 40 36 36 37 40 31 38
例题讲解
身高x 划记 频数
28≤x<30
30≤x<32
32≤x<34
34≤x<36
36≤x<38
38≤x<40
40≤x<42
(1)
组距是2:各组是28 ≤ x< 30 , 30≤ x < 32 ,...
频
数
年龄
12
10
8
6
4
2
0
28 30 32 34 36 38 40 42
拓展练习
4
4
8
7
10
12
3
身高x 划记 频数
25≤x<30
30≤x<35
35≤x<40
40≤x<45
4
15
26
3
组距是5,各组是25 ≤ x< 30 , 30≤ x < 35 ,...
(2)
拓展练习
频
数
年龄
30
25
20
15
10
5
0
25 30 35 40 45
身高x 划记 频数
20≤x<30
30≤x<40
40≤x<50
(3)
4
41
3
频
数
年龄
50
40
30
20
10
0
20 30 40 50
组距是10,各组是20 ≤ x< 30 , 30≤ x < 40 ,...
拓展练习
频
数
年龄
12
10
8
6
4
2
0
28 30 32 34 36 38 40 42
频
数
年龄
30
25
20
15
10
5
0
25 30 35 40 45
频
数
年龄
50
40
30
20
10
0
20 30 40 50
相对而言,组距是5的直方图较好地说明了费尔兹奖得主获奖时的年龄分布.
在分组这个问题上,不是分这么多组就行、分那么多组就不行的,而是怎么样分组更合适一些.
2.一次统计八年级若干名学生每分钟跳绳次
数的频数分布直方图,请根据这个直方图
回答下列问题:
⑴ 参加测试的总人数是多少?
⑵ 自左至右最后一组的频数、频率分别是多少?
⑶ 数据分组时,组距是多少?
8
6
4
2
0
62 87 112 137
频数(人)
跳绳次数
八年级若干名学生每分跳绳次数的频数分布直方图
2
4
6
3
(3)、组距是87-62=25
(1)、2+4+6+3=15人
(2)、频数是3人
频率:3÷15=0.2
拓展练习
解:
3、请观察右图,并回答下列问题:
⑴ 被检查的矿泉水总数有 多少种?
⑵ 被检查的矿泉水的最低 pH为多少?
⑶ 组界为7.9~8.3这一组的 频数、频率分别是多少?
(每一组包括前一个边界 值,不包括后一个边界值)
⑷ 根据我过2001年公布的生活饮用水卫生规范,饮用水的pH应在6.5~8.5的范围内,被检测的矿泉水不符合这一标准的有多少种?占总数的百分之几?
12
10
8
6
4
2
0
5.9 6.3 6.7 7.1 7.5 7.9 8.3
各种矿泉水的pH频数分布直方图
频数(种)
pH
(1)检查的矿泉水总数32种
⑵ 被检查的矿泉水的最低 pH为5.9
⑶ 组界为7.9~8.3这一组的 频数6、频率
(4)被检测的矿泉水不符合这一标准的有5种
占总数的15.625%
拓展练习
解:
4.每年的6月6日是全国的爱眼日,让我们行动起来,爱护我们的眼睛!某校为了做好全校2 000名学生的眼睛保健工作,对学生的视力情况进行一次抽样调查,如图,是利用所得数据绘制的频数直方图.请你根据此图提供的信息,回答下列问题:
(1)本次调查共抽测了 名
(2)视力在4.9及4.9以上的同学约占全校学生比例为 ,全校学生的平均视力是 (精确到百分位)
(3)如果视力在第1,2,3组范围内均属视力不良,那么该校约共有 名学生视力不良,应给予治疗、矫正.
160
37.5 %
4.76
1250
视力
60
第3组
第1组
第2组
第4组
第5组
4.1
4.7
5.0
4.4
5.3
频数(名)
50
40
30
20
10
0
拓展练习
收集
数据
解决数据问题的一般步骤:
整理
数据
描述
数据
分析
数据
课堂小结
20.1 数据的频数分布
第20章 数据的初步分析
沪科版数学八年级下册
第二课时
1.根据具体的问题,学生会选择用直方图描述数据,会确定合适的组距和组数,会准确的画频数分布直方图。
3.培养在实际生活中的统计意识,感受统计知识的应用价值
2、进一步经历数据的整理和表示的过程,能利用简单的频数分布直方图解释数据中蕴含的信息,对实际问题作出判断和决策,初步建立统计概念
教学目标
(1)求极差,即数据中最大值与最小值的差.
(2)决定组距与组数 :组距=极差/组数.
(3) 决定分点:
登记频数,计算频率,列出频率分布表.
画一组数据的频率分布直方图,可以按以下的步骤进行:
(5)画出频率分布直方图.(纵轴表示频率/组距)
知识回顾
计算最大值和最小值的差,可以知道这组数据的变动范围.
(4) 列出频数分布表;
组距:把所有数据分组,每个小组的两个端点之间的距离(组内数据的取值范围)称为组距.
每一小组的频数与数据总数的比值
频率
每一小组数据的出现次数
频数
注意:
1、组距和组数没有确定标准,当数据在 1000个以内时,通常分成5~12组;
知识回顾
2、频数分布直方图中长方形的面积表示数据落在各个小组内的频数
3、在等距离分组中,由于小长方形的面积与高的比是常数(组距),所以在作频数分布直方图时,用小长方形的高表示频数。
1.对某校八(1)班50名学生的年龄进行调查,其中15岁的有2人,14岁的有45人,13岁的有3人,则14岁的频数为_____,频率为 ____。
2.一组数据中共有40个数,其中23出现的频率为0.3,则这40个数中,23出现的频数为____ 。
3.把50个数据分成六组,其中有一组的频数是14,有两组的频数是10,有两组的频率是0.14,则另一组的频数是____ ,频率是____。
知识回顾
45
练一练
0.9
12
0.18
9
39.5
49.5
59.5
69.5
79.5
89.5
99.5
成绩/分
学生人数
5
10
15
20
6
8
10
18
16
2
知识回顾
练一练
4.在对某班的一次测验成绩进行统计中,各分数段的人数如图所示(分数取正整数,满分100分).
(1)该班有多少名学生.
(2)69.5~79.5分这一组的频数是多少?频率是多少?
解:(1)6+8+10+18+16+2=60(人)
(2)由图得: 69.5~79.5分这一组的频数是18
18÷60=0.3
∴69.5~79.5分这一组的频率是0.3
学号 性别 身高 (厘米) 入学成绩
语 数 英
1 女 167 81 88 优
2 男 162 78 85 良
3 女 165 86 90 优
4 男 160 81 99 中
5 女 165 94 86 优
6 女 167 83 75 良
7 女 165 88 94 优
8 男 166 79 98 优
9 女 159 72 65 中
10 男 169 86 97 优
11 男 168 91 96 优
12 男 158 80 93 良
13 男 160 85 89 优
14 女 159 90 84 优
15 女 162 91 89 优
学号 性别 身高 (厘米) 入学成绩
语 数 英
16 女 162 83 85 优
17 女 157 86 80 优
18 女 160 92 93 优
19 男 164 83 89 优
20 女 161 75 77 良
21 男 162 86 97 优
22 男 164 91 91 优
23 女 163 87 82 优
24 男 154 82 88 优
25 男 172 68 70 中
26 男 153 88 95 优
27 男 156 80 87 优
28 男 163 82 81 优
29 男 164 78 75 良
30 女 161 89 87 优
新知探究
下表是某班学生入学时的学生情况,请仔细阅读,完成下列问题
学号 入学成绩
英
1 优
2 良
3 优
4 中
5 优
6 良
7 优
8 优
9 中
10 优
11 优
12 良
13 优
14 优
15 优
学号 入学成绩
英
16 优
17 优
18 优
19 优
20 良
21 优
22 优
23 优
24 优
25 中
26 优
27 优
28 优
29 良
30 优
新知探究
(1)你能用恰当的统计图表表示该班同学入学时的英语成绩吗?
成绩 优 良 中
人数 22 5 3
条形图
从你的图表中能看出大部分同学英语成绩处于哪个等级?
成绩 优 良 中
人数 22 5 3
整体成绩优秀偏多
英语成绩的整体分布情况怎样?
优
新知探究
(2)你能用恰当的统计图表表示该班同学入学时的语文成绩吗?从你的图表中能看出大部分同学处于哪个分数段?成绩的整体分布情况怎样?
成绩 68分 72分 75分 78分 79分 80分 81分 82分 83分
人数 1 1 1 2 1 2 2 2 3
成绩 85分 86分 87分 88分 89分 90分 91分 92分 94分
人数 1 4 1 2 1 1 3 1 1
新知探究
条形图
将语文成绩按10分的距离分段,统计每个分数段的学生数:
成绩段 60~70 70~80 80~90 90~100
人数 1 5 18 6
新知探究
用频数直方图表示
5
10
15
20
60
70
80
90
100
语文成绩
频数(学生人数)
1
5
18
6
从你的图表中能看出大部分同学处于哪个分数段?
频数分布直方图
成绩的整体分布情况怎样?
80--90
80—90人数最多,70分以下人数最少
如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、更直观地反映数据的整体状况.
5
10
15
20
60
70
80
90
100
语文成绩
频数(学生人数)
新知探究
1.条形图各矩形间有空隙,直方图各矩形间无空隙
频数分布直方图的横轴数据是连续的小组的位置是固定的而条形图不是
条形图与频数分布直方图的区别
条形统计图与频数直方图有什么区别和联系?
(1)联系——用途都是可以直观地表示出具体数量.频数直方图是特殊的条形统计图.
(3)绘制的形式不同——条形统计图各条形分开;频数直方图的条形连在一起.
(2)区别——条形统计图是直观地显示出具体数据;频数直方图是表现频数的分布情况.
新知讲解
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
例1 为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100个麦穗,量得它们的长度如下表(单位:cm):
列出样本的频数分布表,画出频数分布直方图,从图表中可以得到什么信息?
例题讲解
解:(1)计算最大值和最小值的差
在样本数据中,最大值是7.4,最小值是4.0,它们的差是
7.4-4.0=3.4
(2)决定组距和组数
最大值与最小值的差是3.4 ,若取组距为0.3 ,那么由于
可以分成12组,组数合适,于是取组距为0.3 ,组数为 12.
例题讲解
例题讲解
(3)确定分点
4.0≤x<4.3
4.3≤x<4.6
4.6≤x<4.9
4.9≤x<5.2
5.2≤x<5.5
5.5≤x<5.8
5.8≤x<6.1
6.1≤x<6.4
6.4≤x<6.7
6.7≤x<7.0
7.0≤x<7.3
7.3≤x<7.6
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
组距为0.3
最小值
例题讲解
(3)列频数分布表
分 组 划 记 频 数
4.0≤x<4.3
4.3≤x<4.6
4.6≤x<4.9
4.9≤x<5.2
5.2≤x<5.5
5.5≤x<5.8
5.8≤x<6.1
6.1≤x<6.4
6.4≤x<6.7
6.7≤x<7.0
7.0≤x<7.3
7.3≤x<7.6
合 计
一
一
丅
正
正正一
正正正
正正正正正
正正
正正一
正正
丅
一
1
1
2
5
11
15
28
13
11
10
2
1
100
6.5 6.4 6.7 5.8 5.9 5.9 5.2 4.0 5.4 4.6
5.8 5.5 6.0 6.5 5.1 6.5 5.3 5.9 5.5 5.8
6.2 5.4 5.0 5.0 6.8 6.0 5.0 5.7 6.0 5.5
6.8 6.0 6.3 5.5 5.0 6.3 5.2 6.0 7.0 6.4
6.4 5.8 5.9 5.7 6.8 6.6 6.0 6.4 5.7 7.4
6.0 5.4 6.5 6.0 6.8 5.8 6.3 6.0 6.3 5.6
5.3 6.4 5.7 6.7 6.2 5.6 6.0 6.7 6.7 6.0
5.5 6.2 6.1 5.3 6.2 6.8 6.6 4.7 5.7 5.7
5.8 5.3 7.0 6.0 6.0 5.9 5.4 6.0 5.2 6.0
6.3 5.7 6.8 6.1 4.5 5.6 6.3 6.0 5.8 6.3
4.0
6.1
5.5
5.2
4.9
4.6
4.3
6.4
5.8
6.7
7.0
7.3
7.6
(4)画频数分布直方图
例题讲解
(4)画频数分布直方图
例题讲解
4.0
从表和图中可以看出,麦穗长度大部分落在5.2 cm至7.0 cm之间,其他区域较少.长度在5.8≤x<6.1范围内的麦穗个数最多,有28个,而长度在4.0≤x<4.3,4.3≤x<4.6, 4.6≤x<4.9, 7.0≤x<7.3, 7.3≤x<7.6 范围内的麦穗个数很少,总共有7个.
例2 下图是某班同学体育课体适能测验—屈膝仰卧起坐的次数分配直方图,请依图回答下列问题:
(1)哪一组次数的人最多?
(2)全班有多少人屈膝仰卧起坐的次数在40次以上(含 40 次)?
(3)全班有多少人屈膝仰卧起坐的次数不到 30 次?
例题讲解
(1)次数为 30~35 的这组人数最多,有10人.
(2)40~45 及 45~50 这两组都是 40 次以上,共有 6+6=12 (人).
(3)20~25 及 25~30 这两组都不到 30 次,共有 6+7=13 (人).
解:
费尔兹奖是国际上享有崇高声誉的一个数学奖项,每4年评选一次,主要授予年轻的数学家,美籍华人丘成桐(1949年出生)1982年获得费尔兹奖.
1、下列数据是截至到今年费尔兹奖得主获奖时的年龄.
29 39 35 33 39 28 33 35
31 31 37 32 38 36 31 39
32 38 37 34 29 34 38 32
35 36 33 29 32 35 36 37
39 38 40 38 37 39 38 34
33 40 36 36 37 40 31 38
拓展练习
请根据下面不同分组列出频数分布表,画出频数分布直方图,比较哪一种分组能更好地说明费尔兹奖得主获奖时的年龄分布:
组距是2:
各组是28 ≤ x< 30 , 30≤ x < 32 ,...
2. 组距是5,
各组是25 ≤ x< 30 , 30≤ x < 35 ,...
3. 组距是10,
各组是20 ≤ x< 30 , 30≤ x < 40 ,...
29 39 35 33 39 28 33 35
31 31 37 32 38 36 31 39
32 38 37 34 29 34 38 32
35 36 33 29 32 35 36 37
39 38 40 38 37 39 38 34
33 40 36 36 37 40 31 38
例题讲解
身高x 划记 频数
28≤x<30
30≤x<32
32≤x<34
34≤x<36
36≤x<38
38≤x<40
40≤x<42
(1)
组距是2:各组是28 ≤ x< 30 , 30≤ x < 32 ,...
频
数
年龄
12
10
8
6
4
2
0
28 30 32 34 36 38 40 42
拓展练习
4
4
8
7
10
12
3
身高x 划记 频数
25≤x<30
30≤x<35
35≤x<40
40≤x<45
4
15
26
3
组距是5,各组是25 ≤ x< 30 , 30≤ x < 35 ,...
(2)
拓展练习
频
数
年龄
30
25
20
15
10
5
0
25 30 35 40 45
身高x 划记 频数
20≤x<30
30≤x<40
40≤x<50
(3)
4
41
3
频
数
年龄
50
40
30
20
10
0
20 30 40 50
组距是10,各组是20 ≤ x< 30 , 30≤ x < 40 ,...
拓展练习
频
数
年龄
12
10
8
6
4
2
0
28 30 32 34 36 38 40 42
频
数
年龄
30
25
20
15
10
5
0
25 30 35 40 45
频
数
年龄
50
40
30
20
10
0
20 30 40 50
相对而言,组距是5的直方图较好地说明了费尔兹奖得主获奖时的年龄分布.
在分组这个问题上,不是分这么多组就行、分那么多组就不行的,而是怎么样分组更合适一些.
2.一次统计八年级若干名学生每分钟跳绳次
数的频数分布直方图,请根据这个直方图
回答下列问题:
⑴ 参加测试的总人数是多少?
⑵ 自左至右最后一组的频数、频率分别是多少?
⑶ 数据分组时,组距是多少?
8
6
4
2
0
62 87 112 137
频数(人)
跳绳次数
八年级若干名学生每分跳绳次数的频数分布直方图
2
4
6
3
(3)、组距是87-62=25
(1)、2+4+6+3=15人
(2)、频数是3人
频率:3÷15=0.2
拓展练习
解:
3、请观察右图,并回答下列问题:
⑴ 被检查的矿泉水总数有 多少种?
⑵ 被检查的矿泉水的最低 pH为多少?
⑶ 组界为7.9~8.3这一组的 频数、频率分别是多少?
(每一组包括前一个边界 值,不包括后一个边界值)
⑷ 根据我过2001年公布的生活饮用水卫生规范,饮用水的pH应在6.5~8.5的范围内,被检测的矿泉水不符合这一标准的有多少种?占总数的百分之几?
12
10
8
6
4
2
0
5.9 6.3 6.7 7.1 7.5 7.9 8.3
各种矿泉水的pH频数分布直方图
频数(种)
pH
(1)检查的矿泉水总数32种
⑵ 被检查的矿泉水的最低 pH为5.9
⑶ 组界为7.9~8.3这一组的 频数6、频率
(4)被检测的矿泉水不符合这一标准的有5种
占总数的15.625%
拓展练习
解:
4.每年的6月6日是全国的爱眼日,让我们行动起来,爱护我们的眼睛!某校为了做好全校2 000名学生的眼睛保健工作,对学生的视力情况进行一次抽样调查,如图,是利用所得数据绘制的频数直方图.请你根据此图提供的信息,回答下列问题:
(1)本次调查共抽测了 名
(2)视力在4.9及4.9以上的同学约占全校学生比例为 ,全校学生的平均视力是 (精确到百分位)
(3)如果视力在第1,2,3组范围内均属视力不良,那么该校约共有 名学生视力不良,应给予治疗、矫正.
160
37.5 %
4.76
1250
视力
60
第3组
第1组
第2组
第4组
第5组
4.1
4.7
5.0
4.4
5.3
频数(名)
50
40
30
20
10
0
拓展练习
收集
数据
解决数据问题的一般步骤:
整理
数据
描述
数据
分析
数据
课堂小结
