北师大新版八年级下册《第2章 一元一次不等式(组)》单元测试卷(8)(word版含答案)
文档属性
| 名称 | 北师大新版八年级下册《第2章 一元一次不等式(组)》单元测试卷(8)(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 195.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 11:17:21 | ||
图片预览




文档简介
北师大新版八年级下册《第2章 一元一次不等式(组)》单元测试卷(8)
一、选择题(本题共计9小题,每题3分,共计27分,)
1.(3分)若a>b,则下列不等式中正确的是( )
A.a﹣b<0 B.﹣5a<﹣5b C.a+8<b﹣8 D.
2.(3分)一袋牛奶的包装盒上标重(200±2)g,则这袋牛奶的实际重量x满足( )
A.x=200g B.x=202g
C.x=202g或198g D.198g≤x≤202g
3.(3分)下列变形中,正确的是( )
A.由2x>﹣x+1得2x﹣x>1 B.由2﹣x<3得﹣x>3﹣2
C.由﹣3x≥﹣6得x≤2 D.由2x≥3得
4.(3分)与不等式<﹣1有相同解集的不等式是( )
A.3x﹣3<(4x+1)﹣1 B.3(x﹣3)<2(2x+1)﹣1
C.2(x﹣3)<3(2x+1)﹣6 D.3x﹣9<4x﹣4
5.(3分)一元一次不等式组的解集为x>5,那么a的取值范围是( )
A.a<5 B.a>5 C.a≤5 D.a≥5
6.(3分)下面列出的不等式中,正确的是( )
A.m与4的差是负数,可表示成m﹣4<0
B.x与2的和是非负数,可表示成x+2>0
C.a不是负数,可表示成a>0
D.x不大于3,可表示成x<3
7.(3分)下列式子属于一元一次不等式的是( )
A.x2﹣5≥2x B.x﹣7>26 C.3x+1 D.x﹣3<2y
8.(3分)不等式>1去分母后得( )
A.2(x﹣1)﹣x﹣2>1 B.2(x﹣1)﹣x+2>1
C.2(x﹣1)﹣x﹣2>4 D.2(x﹣1)﹣x+2>4
9.(3分)不等式组的解集在数轴表示正确的是( )
A. B.
C. D.
二、填空题(本题共计9小题,每题3分,共计27分,)
10.(3分)x与的差的一半再减去是正数,x的取值范围是 .
11.(3分)“m的2倍与8的和不大于2与m的和”用不等式表示为 .
12.(3分)x与3的和不小于6,用不等式表示为 .
13.(3分)不等式6﹣12x<0的解集是 ;3﹣x>1的正整数解为 .
14.(3分)已知关于x的不等式组只有五个整数解,则实数a的取值范围是 .
15.(3分)已知函数y=kx+b和y=mx+n的图象如下,则不等式kx+b>mx+n的解集是 .
16.(3分)步步高超市在2018年初从沃斯商城购进一批智能扫地机器人,进价为800元,出售时标价为1100元,后来由于该商品积压,超市准备打折销售,但要保证利润率不低于10%,则至多可打 折.
17.(3分)一堆玩具分给x个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人分得的玩具不足3件(不为0).则x应满足的不等式组为 .
18.(3分)直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2.则关于x的不等式﹣x+m>nx+4n>0的解集为 .
三、解答题(本题共计7小题,共计66分,)
19.若不等式(2k+1)x<2k+1的解集是x>1,求k的取值范围.
20.解不等式组.
21.解不等式组并把解集在数轴上表示出来.
22.一个两位数,它的个位上的数字比十位上的数字大3,并且这个两位数小于44且大于25,求这个两位数.
23.解不等式组把解集在数轴上表示出来,并求出不等式组的整数解.
24.解不等式(组),并把解在数轴上表示出来
(1)﹣x≥
(2).
25.某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
26.已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
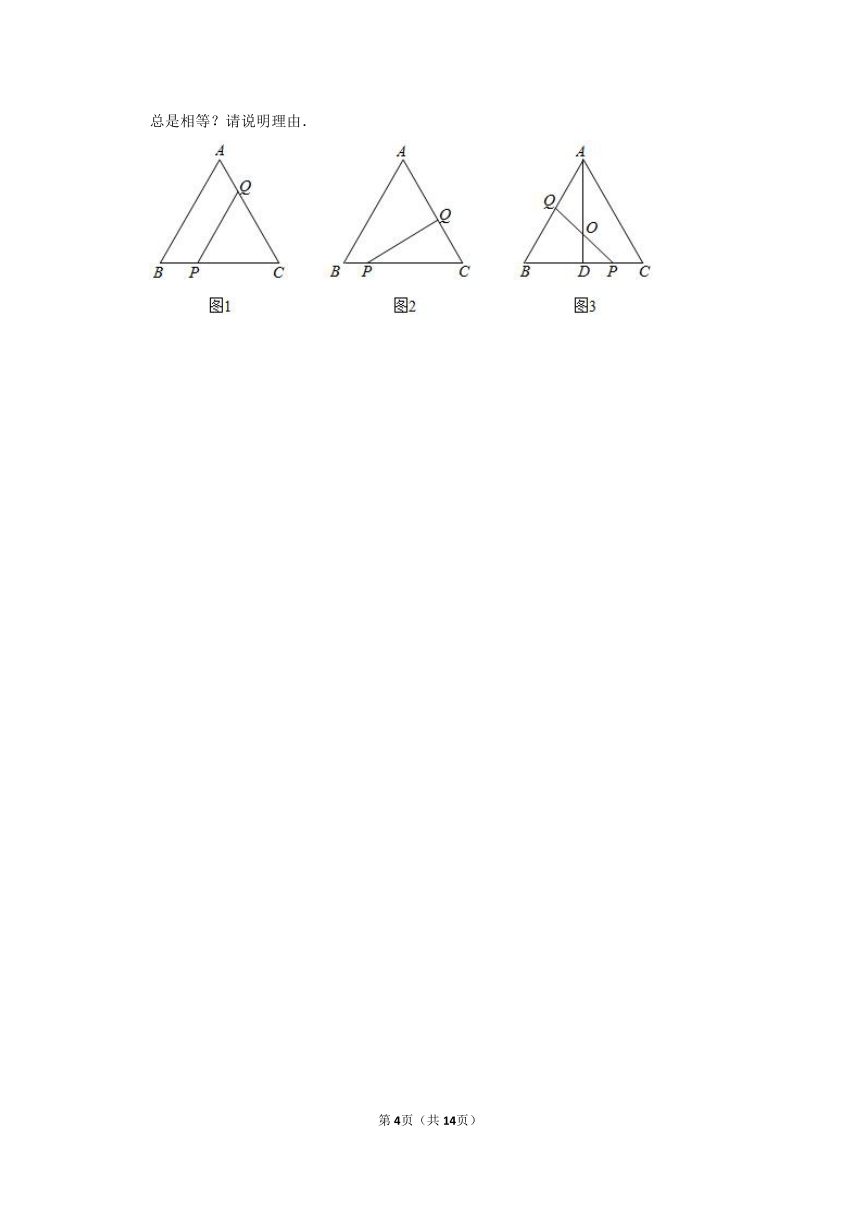
(1)如图1,若PQ∥AB,则x的值为 (s).
(2)如图2,若PQ⊥AC,求x的值.
(3)如图3,当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
北师大新版八年级下册《第2章 一元一次不等式(组)》单元测试卷(8)
参考答案与试题解析
一、选择题(本题共计9小题,每题3分,共计27分,)
1.(3分)若a>b,则下列不等式中正确的是( )
A.a﹣b<0 B.﹣5a<﹣5b C.a+8<b﹣8 D.
【解答】解:A、当a>b时,不等式两边都减b,不等号的方向不变得a﹣b>0,故A错误;
B、当a>b时,不等式两边都乘以﹣5,不等号的方向改变得﹣5a<﹣5b,故B正确;
C、不等式两边的变化必须一致,故C错误;
D、当a>b时,不等式两边都除以4,不等号的方向不变得,故D错误.
故选:B.
2.(3分)一袋牛奶的包装盒上标重(200±2)g,则这袋牛奶的实际重量x满足( )
A.x=200g B.x=202g
C.x=202g或198g D.198g≤x≤202g
【解答】解:∵一袋牛奶的包装盒上标重(200±2)g,
∴(200﹣2)g≤x≤(200+2)g,即198g≤x≤202g.
故选:D.
3.(3分)下列变形中,正确的是( )
A.由2x>﹣x+1得2x﹣x>1 B.由2﹣x<3得﹣x>3﹣2
C.由﹣3x≥﹣6得x≤2 D.由2x≥3得
【解答】解:A,由2x>﹣x+1得2x+x>1,故A选项错误;
B,由2﹣x<3得﹣x<3﹣2;故B选项错误;
C,由﹣3x≥﹣6得x≤2,故C选项正确;
D,由2x≥3得x≥,故D选项错误.
故选:C.
4.(3分)与不等式<﹣1有相同解集的不等式是( )
A.3x﹣3<(4x+1)﹣1 B.3(x﹣3)<2(2x+1)﹣1
C.2(x﹣3)<3(2x+1)﹣6 D.3x﹣9<4x﹣4
【解答】解:去分母得,3(x﹣3)<2(2x+1)﹣6,
去括号、合并得,3x﹣9<4x﹣4,
所以,与不等式<﹣1有相同解集的不等式是3x﹣9<4x﹣4.
故选:D.
5.(3分)一元一次不等式组的解集为x>5,那么a的取值范围是( )
A.a<5 B.a>5 C.a≤5 D.a≥5
【解答】解:∵不等式组的解集为x>5,
∴a≤5,
故选:C.
6.(3分)下面列出的不等式中,正确的是( )
A.m与4的差是负数,可表示成m﹣4<0
B.x与2的和是非负数,可表示成x+2>0
C.a不是负数,可表示成a>0
D.x不大于3,可表示成x<3
【解答】解:A、m与4的差是负数,可表示成m﹣4<0,正确;
B、x与2的和是非负数,可表示成x+2≥0,故此选项错误;
C、a不是负数,可表示成a≥0,故此选项错误;
D、x不大于3,可表示成x≤3,故此选项错误;
故选:A.
7.(3分)下列式子属于一元一次不等式的是( )
A.x2﹣5≥2x B.x﹣7>26 C.3x+1 D.x﹣3<2y
【解答】解:A、未知数的最高次数为2,故选项错误;
B、可化为x>33,符合一元一次不等式的定义,故选项正确;
C、不是不等式,故选项错误.
D,含有两个未知数,故选项错误;
故选:B.
8.(3分)不等式>1去分母后得( )
A.2(x﹣1)﹣x﹣2>1 B.2(x﹣1)﹣x+2>1
C.2(x﹣1)﹣x﹣2>4 D.2(x﹣1)﹣x+2>4
【解答】解:不等式两边都乘以分母的最小公倍数4,得:2(x﹣1)﹣(x﹣2)>4,
即:2(x﹣1)﹣x+2>4,
故选:D.
9.(3分)不等式组的解集在数轴表示正确的是( )
A. B.
C. D.
【解答】解:解不等式x+1≤3,得:x≤2,
解不等式﹣2x﹣6<﹣4,得:x>﹣1,
则不等式组的解集为﹣1<x≤2,
故选:C.
二、填空题(本题共计9小题,每题3分,共计27分,)
10.(3分)x与的差的一半再减去是正数,x的取值范围是 x>2 .
【解答】解:根据题意,可列不等式:×(x﹣)﹣>0,
x﹣﹣>0,
解得x>2,
故答案为x>2.
11.(3分)“m的2倍与8的和不大于2与m的和”用不等式表示为 2m+8≤2+m .
【解答】解:由题意可列不等式为:2m+8≤2+m.
故答案为:2m+8≤2+m.
12.(3分)x与3的和不小于6,用不等式表示为 x+3≥6 .
【解答】解:x与3的和表示为:x+3,由题意可列不等式为:x+3≥6,
故答案为:x+3≥6.
13.(3分)不等式6﹣12x<0的解集是 x> ;3﹣x>1的正整数解为 1 .
【解答】解:由不等式6﹣12x<0,得12x>6,解得x>,
由不等式3﹣x>1,得x<3﹣1,解得x<2,正整数解为1,
故答案为:x>,1.
14.(3分)已知关于x的不等式组只有五个整数解,则实数a的取值范围是 ﹣4≤a<﹣3 .
【解答】解:解不等式x﹣a>0,得:x>a,
解不等式1﹣2x>﹣3,得:x<2,
∵只有五个整数解,
∴﹣4≤a<﹣3,
故答案为:﹣4≤a<﹣3.
15.(3分)已知函数y=kx+b和y=mx+n的图象如下,则不等式kx+b>mx+n的解集是 x>2 .
【解答】解:∵一次函数y=kx+b和y=mx+n的图象交于点P(2,1),
由图象上可以看出:
当x>2时,y=mx+n<kx+b=y,
∴不等式组mx+n<kx+b的解集为:x>2,
故答案为x>2.
16.(3分)步步高超市在2018年初从沃斯商城购进一批智能扫地机器人,进价为800元,出售时标价为1100元,后来由于该商品积压,超市准备打折销售,但要保证利润率不低于10%,则至多可打 8 折.
【解答】解:设打x折,
则1100×﹣800≥800×10%,
解得x≥8,
即至多可打8折,
故答案为:8.
17.(3分)一堆玩具分给x个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人分得的玩具不足3件(不为0).则x应满足的不等式组为 .
【解答】解:根据题意,得
.
18.(3分)直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2.则关于x的不等式﹣x+m>nx+4n>0的解集为 ﹣4<x<﹣2 .
【解答】解:∵直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,
∴关于x的不等式﹣x+m>nx+4n的解集为x<﹣2,
∴y=nx+4n=0时,x=﹣4,
∴不等式﹣x+m>nx+4n>0的解集为﹣4<x<﹣2.
故答案为:﹣4<x<﹣2.
三、解答题(本题共计7小题,共计66分,)
19.若不等式(2k+1)x<2k+1的解集是x>1,求k的取值范围.
【解答】解:∵不等式(2k+1)x<2k+1的解集是x>1,
∴2k+1<0,
解得:k<﹣.
20.解不等式组.
【解答】解:,
由①得,x>3,
由②得,x>1,
故不等式组的解集为:x>3.
21.解不等式组并把解集在数轴上表示出来.
【解答】解:解不等式x+1>0,得:x>﹣1,
解不等式3x﹣8≤﹣x,得:x≤2,
∴不等式组的解集为﹣1<x≤2,
将解集表示在数轴上如下:
22.一个两位数,它的个位上的数字比十位上的数字大3,并且这个两位数小于44且大于25,求这个两位数.
【解答】解:设这个两位数的十位数字为x,则个位数字为(x+3),
依题意,得:,
解得:2<x<3.
∵x为整数,
∴x=3,
∴10x+x+3=36.
答:这个两位数为36.
23.解不等式组把解集在数轴上表示出来,并求出不等式组的整数解.
【解答】解:解不等式①,得
x≥1,
解不等式②,得
x<3,
所以不等式组的解集是1≤x<3,
所以不等式组的整数解为:1,2.
不等式组的解集在数轴上表示为:
24.解不等式(组),并把解在数轴上表示出来
(1)﹣x≥
(2).
【解答】解:(1)去分母得,2x﹣10x≥5(3﹣2x),
去括号得,2x﹣10x≥15﹣10x,
移项得,2x﹣10x+10x≥15,
合并同类项得,2x≥15,
把x的系数化为1得,x≥,
在数轴上表示为:
;
(2),由①得,x≥1,由②得,x<4,
故不等式组的解集为:1≤x<4.
在数轴上表示为:
.
25.某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
【解答】解:设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,
=
x=15,
经检验x=15是原方程的解.
∴40﹣x=25.
甲,乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具y件,则购进乙种玩具(48﹣y)件,
,
解得20≤y<24.
因为y是整数,甲种玩具的件数少于乙种玩具的件数,
∴y取20,21,22,23,
共有4种方案.
26.已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)如图1,若PQ∥AB,则x的值为 (s).
(2)如图2,若PQ⊥AC,求x的值.
(3)如图3,当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
【解答】解:(1)∵∠C=60°,
∴当PC=CQ时,△PQC为等边三角形,
于是∠QPC=60°=∠B,
从而PQ∥AB,
∵PC=4﹣x,CQ=2x,
由4﹣x=2x,
解得:x=,
∴当x=时,PQ∥AB;
故答案为:.
(2)∵PQ⊥AC,∠C=60°,
∴∠QPC=30°,
∴CQ=PC,
即2x=(4﹣x),
解得:x=;
(3)OQ=PO,理由如下:
作QH⊥AD于H,如图3,
∵AD⊥BC,
∴∠QAH=30°,BD=BC=2,
∴QH=AQ=(2x﹣4)=x﹣2,
∵DP=BP﹣BD=x﹣2,
∴QH=DP,
在△OQH和△OPD中,
,
∴△OQH≌△OPD(AAS),
∴OQ=OP.
第1页(共3页)
一、选择题(本题共计9小题,每题3分,共计27分,)
1.(3分)若a>b,则下列不等式中正确的是( )
A.a﹣b<0 B.﹣5a<﹣5b C.a+8<b﹣8 D.
2.(3分)一袋牛奶的包装盒上标重(200±2)g,则这袋牛奶的实际重量x满足( )
A.x=200g B.x=202g
C.x=202g或198g D.198g≤x≤202g
3.(3分)下列变形中,正确的是( )
A.由2x>﹣x+1得2x﹣x>1 B.由2﹣x<3得﹣x>3﹣2
C.由﹣3x≥﹣6得x≤2 D.由2x≥3得
4.(3分)与不等式<﹣1有相同解集的不等式是( )
A.3x﹣3<(4x+1)﹣1 B.3(x﹣3)<2(2x+1)﹣1
C.2(x﹣3)<3(2x+1)﹣6 D.3x﹣9<4x﹣4
5.(3分)一元一次不等式组的解集为x>5,那么a的取值范围是( )
A.a<5 B.a>5 C.a≤5 D.a≥5
6.(3分)下面列出的不等式中,正确的是( )
A.m与4的差是负数,可表示成m﹣4<0
B.x与2的和是非负数,可表示成x+2>0
C.a不是负数,可表示成a>0
D.x不大于3,可表示成x<3
7.(3分)下列式子属于一元一次不等式的是( )
A.x2﹣5≥2x B.x﹣7>26 C.3x+1 D.x﹣3<2y
8.(3分)不等式>1去分母后得( )
A.2(x﹣1)﹣x﹣2>1 B.2(x﹣1)﹣x+2>1
C.2(x﹣1)﹣x﹣2>4 D.2(x﹣1)﹣x+2>4
9.(3分)不等式组的解集在数轴表示正确的是( )
A. B.
C. D.
二、填空题(本题共计9小题,每题3分,共计27分,)
10.(3分)x与的差的一半再减去是正数,x的取值范围是 .
11.(3分)“m的2倍与8的和不大于2与m的和”用不等式表示为 .
12.(3分)x与3的和不小于6,用不等式表示为 .
13.(3分)不等式6﹣12x<0的解集是 ;3﹣x>1的正整数解为 .
14.(3分)已知关于x的不等式组只有五个整数解,则实数a的取值范围是 .
15.(3分)已知函数y=kx+b和y=mx+n的图象如下,则不等式kx+b>mx+n的解集是 .
16.(3分)步步高超市在2018年初从沃斯商城购进一批智能扫地机器人,进价为800元,出售时标价为1100元,后来由于该商品积压,超市准备打折销售,但要保证利润率不低于10%,则至多可打 折.
17.(3分)一堆玩具分给x个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人分得的玩具不足3件(不为0).则x应满足的不等式组为 .
18.(3分)直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2.则关于x的不等式﹣x+m>nx+4n>0的解集为 .
三、解答题(本题共计7小题,共计66分,)
19.若不等式(2k+1)x<2k+1的解集是x>1,求k的取值范围.
20.解不等式组.
21.解不等式组并把解集在数轴上表示出来.
22.一个两位数,它的个位上的数字比十位上的数字大3,并且这个两位数小于44且大于25,求这个两位数.
23.解不等式组把解集在数轴上表示出来,并求出不等式组的整数解.
24.解不等式(组),并把解在数轴上表示出来
(1)﹣x≥
(2).
25.某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
26.已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)如图1,若PQ∥AB,则x的值为 (s).
(2)如图2,若PQ⊥AC,求x的值.
(3)如图3,当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
北师大新版八年级下册《第2章 一元一次不等式(组)》单元测试卷(8)
参考答案与试题解析
一、选择题(本题共计9小题,每题3分,共计27分,)
1.(3分)若a>b,则下列不等式中正确的是( )
A.a﹣b<0 B.﹣5a<﹣5b C.a+8<b﹣8 D.
【解答】解:A、当a>b时,不等式两边都减b,不等号的方向不变得a﹣b>0,故A错误;
B、当a>b时,不等式两边都乘以﹣5,不等号的方向改变得﹣5a<﹣5b,故B正确;
C、不等式两边的变化必须一致,故C错误;
D、当a>b时,不等式两边都除以4,不等号的方向不变得,故D错误.
故选:B.
2.(3分)一袋牛奶的包装盒上标重(200±2)g,则这袋牛奶的实际重量x满足( )
A.x=200g B.x=202g
C.x=202g或198g D.198g≤x≤202g
【解答】解:∵一袋牛奶的包装盒上标重(200±2)g,
∴(200﹣2)g≤x≤(200+2)g,即198g≤x≤202g.
故选:D.
3.(3分)下列变形中,正确的是( )
A.由2x>﹣x+1得2x﹣x>1 B.由2﹣x<3得﹣x>3﹣2
C.由﹣3x≥﹣6得x≤2 D.由2x≥3得
【解答】解:A,由2x>﹣x+1得2x+x>1,故A选项错误;
B,由2﹣x<3得﹣x<3﹣2;故B选项错误;
C,由﹣3x≥﹣6得x≤2,故C选项正确;
D,由2x≥3得x≥,故D选项错误.
故选:C.
4.(3分)与不等式<﹣1有相同解集的不等式是( )
A.3x﹣3<(4x+1)﹣1 B.3(x﹣3)<2(2x+1)﹣1
C.2(x﹣3)<3(2x+1)﹣6 D.3x﹣9<4x﹣4
【解答】解:去分母得,3(x﹣3)<2(2x+1)﹣6,
去括号、合并得,3x﹣9<4x﹣4,
所以,与不等式<﹣1有相同解集的不等式是3x﹣9<4x﹣4.
故选:D.
5.(3分)一元一次不等式组的解集为x>5,那么a的取值范围是( )
A.a<5 B.a>5 C.a≤5 D.a≥5
【解答】解:∵不等式组的解集为x>5,
∴a≤5,
故选:C.
6.(3分)下面列出的不等式中,正确的是( )
A.m与4的差是负数,可表示成m﹣4<0
B.x与2的和是非负数,可表示成x+2>0
C.a不是负数,可表示成a>0
D.x不大于3,可表示成x<3
【解答】解:A、m与4的差是负数,可表示成m﹣4<0,正确;
B、x与2的和是非负数,可表示成x+2≥0,故此选项错误;
C、a不是负数,可表示成a≥0,故此选项错误;
D、x不大于3,可表示成x≤3,故此选项错误;
故选:A.
7.(3分)下列式子属于一元一次不等式的是( )
A.x2﹣5≥2x B.x﹣7>26 C.3x+1 D.x﹣3<2y
【解答】解:A、未知数的最高次数为2,故选项错误;
B、可化为x>33,符合一元一次不等式的定义,故选项正确;
C、不是不等式,故选项错误.
D,含有两个未知数,故选项错误;
故选:B.
8.(3分)不等式>1去分母后得( )
A.2(x﹣1)﹣x﹣2>1 B.2(x﹣1)﹣x+2>1
C.2(x﹣1)﹣x﹣2>4 D.2(x﹣1)﹣x+2>4
【解答】解:不等式两边都乘以分母的最小公倍数4,得:2(x﹣1)﹣(x﹣2)>4,
即:2(x﹣1)﹣x+2>4,
故选:D.
9.(3分)不等式组的解集在数轴表示正确的是( )
A. B.
C. D.
【解答】解:解不等式x+1≤3,得:x≤2,
解不等式﹣2x﹣6<﹣4,得:x>﹣1,
则不等式组的解集为﹣1<x≤2,
故选:C.
二、填空题(本题共计9小题,每题3分,共计27分,)
10.(3分)x与的差的一半再减去是正数,x的取值范围是 x>2 .
【解答】解:根据题意,可列不等式:×(x﹣)﹣>0,
x﹣﹣>0,
解得x>2,
故答案为x>2.
11.(3分)“m的2倍与8的和不大于2与m的和”用不等式表示为 2m+8≤2+m .
【解答】解:由题意可列不等式为:2m+8≤2+m.
故答案为:2m+8≤2+m.
12.(3分)x与3的和不小于6,用不等式表示为 x+3≥6 .
【解答】解:x与3的和表示为:x+3,由题意可列不等式为:x+3≥6,
故答案为:x+3≥6.
13.(3分)不等式6﹣12x<0的解集是 x> ;3﹣x>1的正整数解为 1 .
【解答】解:由不等式6﹣12x<0,得12x>6,解得x>,
由不等式3﹣x>1,得x<3﹣1,解得x<2,正整数解为1,
故答案为:x>,1.
14.(3分)已知关于x的不等式组只有五个整数解,则实数a的取值范围是 ﹣4≤a<﹣3 .
【解答】解:解不等式x﹣a>0,得:x>a,
解不等式1﹣2x>﹣3,得:x<2,
∵只有五个整数解,
∴﹣4≤a<﹣3,
故答案为:﹣4≤a<﹣3.
15.(3分)已知函数y=kx+b和y=mx+n的图象如下,则不等式kx+b>mx+n的解集是 x>2 .
【解答】解:∵一次函数y=kx+b和y=mx+n的图象交于点P(2,1),
由图象上可以看出:
当x>2时,y=mx+n<kx+b=y,
∴不等式组mx+n<kx+b的解集为:x>2,
故答案为x>2.
16.(3分)步步高超市在2018年初从沃斯商城购进一批智能扫地机器人,进价为800元,出售时标价为1100元,后来由于该商品积压,超市准备打折销售,但要保证利润率不低于10%,则至多可打 8 折.
【解答】解:设打x折,
则1100×﹣800≥800×10%,
解得x≥8,
即至多可打8折,
故答案为:8.
17.(3分)一堆玩具分给x个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人分得的玩具不足3件(不为0).则x应满足的不等式组为 .
【解答】解:根据题意,得
.
18.(3分)直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2.则关于x的不等式﹣x+m>nx+4n>0的解集为 ﹣4<x<﹣2 .
【解答】解:∵直线y=﹣x+m与y=nx+4n(n≠0)的交点的横坐标为﹣2,
∴关于x的不等式﹣x+m>nx+4n的解集为x<﹣2,
∴y=nx+4n=0时,x=﹣4,
∴不等式﹣x+m>nx+4n>0的解集为﹣4<x<﹣2.
故答案为:﹣4<x<﹣2.
三、解答题(本题共计7小题,共计66分,)
19.若不等式(2k+1)x<2k+1的解集是x>1,求k的取值范围.
【解答】解:∵不等式(2k+1)x<2k+1的解集是x>1,
∴2k+1<0,
解得:k<﹣.
20.解不等式组.
【解答】解:,
由①得,x>3,
由②得,x>1,
故不等式组的解集为:x>3.
21.解不等式组并把解集在数轴上表示出来.
【解答】解:解不等式x+1>0,得:x>﹣1,
解不等式3x﹣8≤﹣x,得:x≤2,
∴不等式组的解集为﹣1<x≤2,
将解集表示在数轴上如下:
22.一个两位数,它的个位上的数字比十位上的数字大3,并且这个两位数小于44且大于25,求这个两位数.
【解答】解:设这个两位数的十位数字为x,则个位数字为(x+3),
依题意,得:,
解得:2<x<3.
∵x为整数,
∴x=3,
∴10x+x+3=36.
答:这个两位数为36.
23.解不等式组把解集在数轴上表示出来,并求出不等式组的整数解.
【解答】解:解不等式①,得
x≥1,
解不等式②,得
x<3,
所以不等式组的解集是1≤x<3,
所以不等式组的整数解为:1,2.
不等式组的解集在数轴上表示为:
24.解不等式(组),并把解在数轴上表示出来
(1)﹣x≥
(2).
【解答】解:(1)去分母得,2x﹣10x≥5(3﹣2x),
去括号得,2x﹣10x≥15﹣10x,
移项得,2x﹣10x+10x≥15,
合并同类项得,2x≥15,
把x的系数化为1得,x≥,
在数轴上表示为:
;
(2),由①得,x≥1,由②得,x<4,
故不等式组的解集为:1≤x<4.
在数轴上表示为:
.
25.某商场计划购进一批甲、乙两种玩具,已知一件甲种玩具的进价与一件乙种玩具的进价的和为40元,用90元购进甲种玩具的件数与用150元购进乙种玩具的件数相同.
(1)求每件甲种、乙种玩具的进价分别是多少元?
(2)商场计划购进甲、乙两种玩具共48件,其中甲种玩具的件数少于乙种玩具的件数,商场决定此次进货的总资金不超过1000元,求商场共有几种进货方案?
【解答】解:设甲种玩具进价x元/件,则乙种玩具进价为(40﹣x)元/件,
=
x=15,
经检验x=15是原方程的解.
∴40﹣x=25.
甲,乙两种玩具分别是15元/件,25元/件;
(2)设购进甲种玩具y件,则购进乙种玩具(48﹣y)件,
,
解得20≤y<24.
因为y是整数,甲种玩具的件数少于乙种玩具的件数,
∴y取20,21,22,23,
共有4种方案.
26.已知等边△ABC的边长为4cm,点P,Q分别从B,C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s;点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为x(s).
(1)如图1,若PQ∥AB,则x的值为 (s).
(2)如图2,若PQ⊥AC,求x的值.
(3)如图3,当点Q在AB上运动时,PQ与△ABC的高AD交于点O,OQ与OP是否总是相等?请说明理由.
【解答】解:(1)∵∠C=60°,
∴当PC=CQ时,△PQC为等边三角形,
于是∠QPC=60°=∠B,
从而PQ∥AB,
∵PC=4﹣x,CQ=2x,
由4﹣x=2x,
解得:x=,
∴当x=时,PQ∥AB;
故答案为:.
(2)∵PQ⊥AC,∠C=60°,
∴∠QPC=30°,
∴CQ=PC,
即2x=(4﹣x),
解得:x=;
(3)OQ=PO,理由如下:
作QH⊥AD于H,如图3,
∵AD⊥BC,
∴∠QAH=30°,BD=BC=2,
∴QH=AQ=(2x﹣4)=x﹣2,
∵DP=BP﹣BD=x﹣2,
∴QH=DP,
在△OQH和△OPD中,
,
∴△OQH≌△OPD(AAS),
∴OQ=OP.
第1页(共3页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
