北师大新版八年级下册《第4章 因式分解》单元测试卷(2)(word版含答案)
文档属性
| 名称 | 北师大新版八年级下册《第4章 因式分解》单元测试卷(2)(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 208.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 11:25:35 | ||
图片预览




文档简介
北师大新版八年级下册《第4章 因式分解》单元测试卷(2)
一、选择题(每小题3分,共30分)
1.(3分)下列因式分解正确的是( )
A.x2﹣x=x(x+1) B.a2﹣3a﹣4=(a+4)(a﹣1)
C.a2+2ab﹣b2=(a﹣b)2 D.x2﹣y2=(x+y)(x﹣y)
2.(3分)把a2x+ay﹣a3xy因式分解时,应提取的公因式是( )
A.a2 B.a C.ax D.ay
3.(3分)下列各式能够用完全平方公式因式分解的是( )
A.4x2+1 B.4x2+4x+1 C.4x2+4x﹣1 D.4x2﹣4x﹣1
4.(3分)王老师布置了5道因式分解的题,小明同学的答案如下,你认为他做对的题的序号是( )
①1+4x2=(1+2x)2;②6xyz﹣8xy2=2xyz(3﹣4y);③4x+2y﹣6z=2(2x+y﹣3z);④a2﹣2ab+b2=(a﹣b)2;⑤x2y﹣4y=y(x2﹣4).
A.①② B.③④ C.④⑤ D.②③④⑤
5.(3分)将下列多项式因式分解,结果中不含有因式a+1的是( )
A.a2﹣1 B.a2+a
C.a2+a﹣2 D.(a+2)2﹣2(a+2)+1
6.(3分)若关于x的二次三项式x2﹣kx﹣b因式分解为(x﹣1)(x﹣3),则k+b的值为( )
A.﹣1 B.1 C.﹣7 D.7
7.(3分)在探索因式分解的公式时,可以借助几何图形来解释某些公式.如图,从左图到右图的变化过程中,解释的因式分解公式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.a2﹣b2=(a+b)(a﹣b)
C.a2+b2=(a+b)2 D.(a﹣b)2=a2﹣2ab+b2
8.(3分)若+q2﹣8q+16=0,则因式分解(x2+y2)﹣(pxy+q)的结果是( )
A.(x﹣y)2﹣4 B.(x﹣y﹣2)(x﹣y+2)
C.(x﹣y+2)2 D.(x+y﹣2)(x+y+2)
9.(3分)要在二次三项式x2+□x﹣6的□中填上一个整数,使它能按x2+(a+b)x+ab型分解为(x+a)(x+b)的形式,那么这些数只能是( )
A.1,﹣1 B.5,﹣5
C.1,﹣1,5,﹣5 D.以上答案都不对
10.(3分)已知三个实数a,b,c满足a﹣2b+c=0,a+2b+c<0,则( )
A.b>0,b2﹣ac≤0 B.b<0,b2﹣ac≤0
C.b>0,b2﹣ac≥0 D.b<0,b2﹣ac≥0
二、填空题(每小题3分,共18分)
11.(3分)已知a2+a=0,则2a2+2a+2021= .
12.(3分)有下列各组代数式:①5a﹣5b和5a+5b;②ax+y和x+ay;③a3+2a2b+ab2和a2+ab;④x2﹣4y2和2xy+y2.其中没有公因式的是 (只填序号).
13.(3分)已知关于x的代数式x2﹣(a+1)x+9是完全平方式,则a= .
14.(3分)为了烘托新年的节日氛围,市政部门在某广场上用鲜花摆放了一个圆形花坛.已知该花坛的面积为(πa2+18πab+81πb2)平方米(a>0,b>0),则这个圆形花坛的半径为 米.
15.(3分)在完成因式分解的练习时,小明不小心将一道题4x3弄上了污渍,他只记得将这个多项式因式分解时应先提公因式,再用平方差公式分解,请你帮小明想一想,老师布置的原题可能是 ,因式分解的结果是 .(填一个合适的即可)
16.(3分)如图,甲类纸片是边长为x的正方形,乙类纸片是边长为y的正方形,丙类纸片是长、宽分别为x和y的长方形.现有甲类纸片1张,乙类纸片4张,则应取 张丙类纸片,才能用它们拼成一个新的正方形,拼成的正方形的边长为 .
三、解答题(共52分)
17.(6分)把下列各式因式分解:
(1)(a+b)2+a+b+;
(2)8(x2﹣2y2)﹣x(7x+y)+xy.
18.(6分)用简便方法计算:
(1)﹣23.7×+×1.3﹣2.6×;
(2)2020+20202﹣20212.
19.(6分)如图,边长为a,b的长方形,它的周长为14,面积为10,求下列各式的值:
(1)a2b+ab2;
(2)a2+b2+ab
20.(6分)先分解因式,再求值:
(1)15a2(b+4)﹣30a(b+4),其中a=2,b=﹣2;
(2)(x2+y2)2﹣4x2y2,其中x=3.5,y=1.5.
21.(6分)已知a、b、c分别是△ABC的三边.
(1)分别将多项式a2c2﹣b2c2,a4﹣b4进行因式分解,
(2)若a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状,并说明理由.
22.(6分)完全平方公式是初中数学的重要公式之一:(a+b)2=a2+2ab+b2,完全平方公式既可以用来进行整式计算又可以用来进行分解因式.
发现:3+2=2+2+1=()2+2+12=(+1)2;
应用:
(1)写出一个能用上面方法进行因式分解的式子,并进行因式分解;
(2)若a+b=(m+n)2,请用m,n表示a,b.
拓展:如图在Rt△ABC中,BC=1,AC=,∠C=90°,延长CA至点D,使AD=AB,求BD的长.(参考上面提供的方法把结果进行化简)
23.(8分)阅读材料并解决问题.
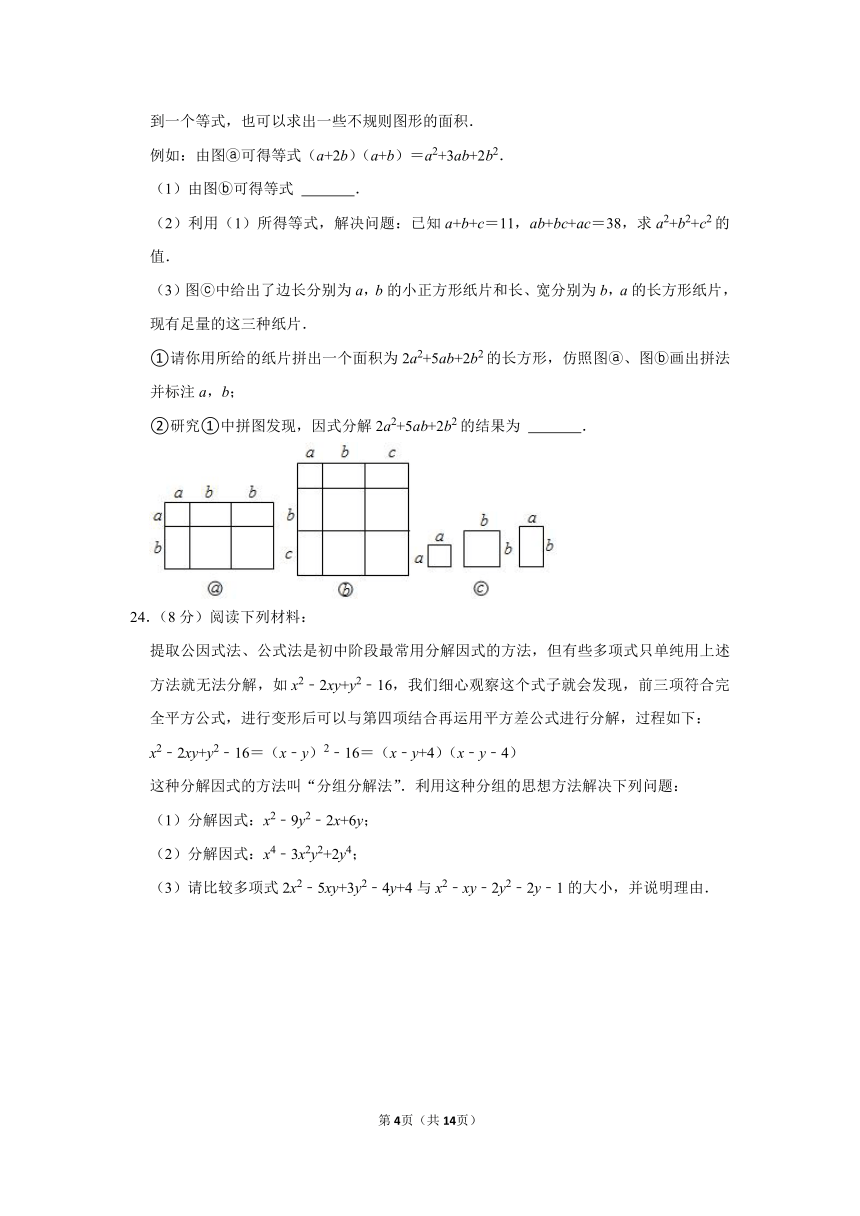
把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如:由图 可得等式(a+2b)(a+b)=a2+3ab+2b2.
(1)由图 可得等式 .
(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)图 中给出了边长分别为a,b的小正方形纸片和长、宽分别为b,a的长方形纸片,现有足量的这三种纸片.
①请你用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,仿照图 、图 画出拼法并标注a,b;
②研究①中拼图发现,因式分解2a2+5ab+2b2的结果为 .
24.(8分)阅读下列材料:
提取公因式法、公式法是初中阶段最常用分解因式的方法,但有些多项式只单纯用上述方法就无法分解,如x2﹣2xy+y2﹣16,我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解,过程如下:
x2﹣2xy+y2﹣16=(x﹣y)2﹣16=(x﹣y+4)(x﹣y﹣4)
这种分解因式的方法叫“分组分解法”.利用这种分组的思想方法解决下列问题:
(1)分解因式:x2﹣9y2﹣2x+6y;
(2)分解因式:x4﹣3x2y2+2y4;
(3)请比较多项式2x2﹣5xy+3y2﹣4y+4与x2﹣xy﹣2y2﹣2y﹣1的大小,并说明理由.
北师大新版八年级下册《第4章 因式分解》单元测试卷(2)
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列因式分解正确的是( )
A.x2﹣x=x(x+1) B.a2﹣3a﹣4=(a+4)(a﹣1)
C.a2+2ab﹣b2=(a﹣b)2 D.x2﹣y2=(x+y)(x﹣y)
【解答】解:A、原式=x(x﹣1),错误;
B、原式=(a﹣4)(a+1),错误;
C、a2+2ab﹣b2,不能分解因式,错误;
D、原式=(x+y)(x﹣y),正确.
故选:D.
2.(3分)把a2x+ay﹣a3xy因式分解时,应提取的公因式是( )
A.a2 B.a C.ax D.ay
【解答】解:把a2x+ay﹣a3xy因式分解时,应提取的公因式是a.
故选:B.
3.(3分)下列各式能够用完全平方公式因式分解的是( )
A.4x2+1 B.4x2+4x+1 C.4x2+4x﹣1 D.4x2﹣4x﹣1
【解答】解:A、4x2+1,不符合完全平方公式的特征,不合题意;
B、4x2+4x+1=(2x+1)2,符合完全平方公式的特征,符合题意;
C、4x2+4x﹣1,不符合完全平方公式的特征,不合题意;
D、4x2﹣4x﹣1,不符合完全平方公式的特征,不合题意;
故选:B.
4.(3分)王老师布置了5道因式分解的题,小明同学的答案如下,你认为他做对的题的序号是( )
①1+4x2=(1+2x)2;②6xyz﹣8xy2=2xyz(3﹣4y);③4x+2y﹣6z=2(2x+y﹣3z);④a2﹣2ab+b2=(a﹣b)2;⑤x2y﹣4y=y(x2﹣4).
A.①② B.③④ C.④⑤ D.②③④⑤
【解答】解:①1+4x2,不符合完全平方公式的特征,不能分解因式,故①错误;
②6xyz﹣8xy2=2xy(3z﹣4y),故②错误;
③4x+2y﹣6z=2(2x+y﹣3z),故③正确;
④a2﹣2ab+b2=(a﹣b)2,故④正确;
⑤x2y﹣4y=y(x2﹣4)=y(x+2)(x﹣2)故⑤错误.
故选:B.
5.(3分)将下列多项式因式分解,结果中不含有因式a+1的是( )
A.a2﹣1 B.a2+a
C.a2+a﹣2 D.(a+2)2﹣2(a+2)+1
【解答】解:∵a2﹣1=(a+1)(a﹣1),
a2+a=a(a+1),
a2+a﹣2=(a+2)(a﹣1),
(a+2)2﹣2(a+2)+1=(a+2﹣1)2=(a+1)2,
∴结果中不含有因式a+1的是选项C;
故选:C.
6.(3分)若关于x的二次三项式x2﹣kx﹣b因式分解为(x﹣1)(x﹣3),则k+b的值为( )
A.﹣1 B.1 C.﹣7 D.7
【解答】解:根据题意得:x2﹣kx﹣b=(x﹣1)(x﹣3)=x2﹣4x+3,
∴k=4,b=﹣3,
则k+b=1,
故选:B.
7.(3分)在探索因式分解的公式时,可以借助几何图形来解释某些公式.如图,从左图到右图的变化过程中,解释的因式分解公式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.a2﹣b2=(a+b)(a﹣b)
C.a2+b2=(a+b)2 D.(a﹣b)2=a2﹣2ab+b2
【解答】解:如图,从左图到右图的变化过程中,解释的因式分解公式是:a2﹣b2=(a+b)(a﹣b),
故选:B.
8.(3分)若+q2﹣8q+16=0,则因式分解(x2+y2)﹣(pxy+q)的结果是( )
A.(x﹣y)2﹣4 B.(x﹣y﹣2)(x﹣y+2)
C.(x﹣y+2)2 D.(x+y﹣2)(x+y+2)
【解答】解:∵+q2﹣8q+16=0,
∴+(q﹣4)2=0,
∴p﹣2=0,q﹣4=0,
解得p=2,q=4,
∴(x2+y2)﹣(pxy+q)
=(x2+y2)﹣(2xy+4)
=(x2+y2﹣2xy)﹣4
=(x﹣y)2﹣4
=(x﹣y+2)(x﹣y﹣2).
故选:B.
9.(3分)要在二次三项式x2+□x﹣6的□中填上一个整数,使它能按x2+(a+b)x+ab型分解为(x+a)(x+b)的形式,那么这些数只能是( )
A.1,﹣1 B.5,﹣5
C.1,﹣1,5,﹣5 D.以上答案都不对
【解答】解:﹣6可以分成:﹣2×3,2×(﹣3),﹣1×6,1×(﹣6),
□中填上的整数应该是﹣6的两个因数的和,即1,﹣1,5,﹣5.
故选:C.
10.(3分)已知三个实数a,b,c满足a﹣2b+c=0,a+2b+c<0,则( )
A.b>0,b2﹣ac≤0 B.b<0,b2﹣ac≤0
C.b>0,b2﹣ac≥0 D.b<0,b2﹣ac≥0
【解答】解:∵a﹣2b+c=0,a+2b+c<0,
∴a+c=2b,b=,
∴a+2b+c=(a+c)+2b=4b<0,
∴b<0,
∴b2﹣ac==﹣ac==≥0,
即b<0,b2﹣ac≥0,
故选:D.
二、填空题(每小题3分,共18分)
11.(3分)已知a2+a=0,则2a2+2a+2021= 2021 .
【解答】解:∵a2+a=0,
∴2a2+2a+2021
=2(a2+a)+2021
=2×0+2021
=0+2021
=2021.
故答案为:2021.
12.(3分)有下列各组代数式:①5a﹣5b和5a+5b;②ax+y和x+ay;③a3+2a2b+ab2和a2+ab;④x2﹣4y2和2xy+y2.其中没有公因式的是 ②④ (只填序号).
【解答】解:①5a﹣5b和5a+5b有公因式,公因式为5;
②ax+y和x+ay没有公因式;
③a3+2a2b+ab2和a2+ab有公因式,公因式为a(a+b);
④x2﹣4y2和2xy+y2没有公因式.
没有公因式的是②④.
故答案为:②④.
13.(3分)已知关于x的代数式x2﹣(a+1)x+9是完全平方式,则a= 5或﹣7 .
【解答】解:∵关于x的代数式x2﹣(a+1)x+9是完全平方式,
∴x2﹣(a+1)x+32=(x±3)2,
∴a+1=±6,
解得:a=5或a=﹣7.
故答案为:5或﹣7.
14.(3分)为了烘托新年的节日氛围,市政部门在某广场上用鲜花摆放了一个圆形花坛.已知该花坛的面积为(πa2+18πab+81πb2)平方米(a>0,b>0),则这个圆形花坛的半径为 (a+9b) 米.
【解答】解:∵πa2+18πab+81πb2
=π(a2+18ab+81b2)
=π(a+9b)2
=πr2,
∴r=a+9b,
故答案为:(a+9b).
15.(3分)在完成因式分解的练习时,小明不小心将一道题4x3弄上了污渍,他只记得将这个多项式因式分解时应先提公因式,再用平方差公式分解,请你帮小明想一想,老师布置的原题可能是 4x3﹣9x(答案不唯一) ,因式分解的结果是 x(2x+3)(2x﹣3) .(填一个合适的即可)
【解答】解:老师布置的题目可能是4x3﹣9x(答案不唯一),
其因式分解的结果为:4x3﹣9x=x(4x2﹣9)=x(2x+3)(2x﹣3),
故答案为:4x3﹣9x(答案不唯一),x(2x+3)(2x﹣3).
16.(3分)如图,甲类纸片是边长为x的正方形,乙类纸片是边长为y的正方形,丙类纸片是长、宽分别为x和y的长方形.现有甲类纸片1张,乙类纸片4张,则应取 4 张丙类纸片,才能用它们拼成一个新的正方形,拼成的正方形的边长为 x+2y .
【解答】解:甲类纸片1张,面积为x2;乙类纸片4张,面积为4y2.
设至少取丙类纸片a张才能用它们拼成一个新的正方形,
∵x2+4y2+axy是一个完全平方式,
∴a应取4,
即丙类纸片应取4张.
∵x2+4y2+4xy=(x+2y)2,
∴拼成的正方形的边长为x+2y.
故答案为:4,x+2y.
三、解答题(共52分)
17.(6分)把下列各式因式分解:
(1)(a+b)2+a+b+;
(2)8(x2﹣2y2)﹣x(7x+y)+xy.
【解答】解:(1)原式=(a+b+)2.
(2)8(x2﹣2y2)﹣x(7x+y)+xy
=8x2﹣16y2﹣7x2﹣xy+xy
=x2﹣16y2
=(x+4y)(x﹣4y).
18.(6分)用简便方法计算:
(1)﹣23.7×+×1.3﹣2.6×;
(2)2020+20202﹣20212.
【解答】解:(1)原式=×(﹣23.7+1.3﹣2.6)
=×(﹣25)
=﹣20.
(2)原式=2020﹣(20212﹣20202)
=2020﹣(2021+2020)×(2021﹣2020)
=2020﹣2021﹣2020
=﹣2021.
19.(6分)如图,边长为a,b的长方形,它的周长为14,面积为10,求下列各式的值:
(1)a2b+ab2;
(2)a2+b2+ab
【解答】解:(1)∵a+b=7,ab=10,
∴a2b+ab2=ab(a+b)=70;
(2)a2+b2=(a+b)2﹣2ab=72﹣2×10=29,
∴a2+b2+ab=29+10=39.
20.(6分)先分解因式,再求值:
(1)15a2(b+4)﹣30a(b+4),其中a=2,b=﹣2;
(2)(x2+y2)2﹣4x2y2,其中x=3.5,y=1.5.
【解答】解:(1)原式=15a(b+4)(a﹣2)
当a=2,b=﹣2时,
原式=15×2×(﹣2+4)×(2﹣2)=0;
(2)原式=(x2+2xy+y2)(x2﹣2xy+y2)
=(x+y)2(x﹣y)2
当x=3.5,y=1.5时,
原式=(3.5+1.5)2×(3.5﹣1.5)2=100.
21.(6分)已知a、b、c分别是△ABC的三边.
(1)分别将多项式a2c2﹣b2c2,a4﹣b4进行因式分解,
(2)若a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状,并说明理由.
【解答】解:(1)a2c2﹣b2c2=c2(a2﹣b2)=c2(a+b)(a﹣b);
a4﹣b4=(a2﹣b2)(a2+b2)=(a﹣b)(a+b)(a2+b2);
(2)∵a2c2﹣b2c2=a4﹣b4,
∴c2(a+b)(a﹣b)=(a﹣b)(a+b)(a2+b2);
∴c2(a+b)(a﹣b)﹣(a﹣b)(a+b)(a2+b2)=0;
∴(a+b)(a﹣b)(c2﹣a2﹣b2)=0,
∵a、b、c分别是△ABC的三边.
∴a﹣b=0或c2﹣a2﹣b2=0,
∴a=b或c2=a2+b2,
∴△ABC为等腰三角形或直角三角形.
22.(6分)完全平方公式是初中数学的重要公式之一:(a+b)2=a2+2ab+b2,完全平方公式既可以用来进行整式计算又可以用来进行分解因式.
发现:3+2=2+2+1=()2+2+12=(+1)2;
应用:
(1)写出一个能用上面方法进行因式分解的式子,并进行因式分解;
(2)若a+b=(m+n)2,请用m,n表示a,b.
拓展:如图在Rt△ABC中,BC=1,AC=,∠C=90°,延长CA至点D,使AD=AB,求BD的长.(参考上面提供的方法把结果进行化简)
【解答】解:(1)4+2=3+2+1=;
(2)∵a+b=(m+n)2,
∴a+b=m2+2n2+2mn,
∴a=m2+2n2,b=2mn;
拓展:由题意得,AB=,
∴AD=AB=2,
∴CD=+2,
∴BD2=BC2+CD2=1+=6+4+2==,
∴BD=.
23.(8分)阅读材料并解决问题.
把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如:由图 可得等式(a+2b)(a+b)=a2+3ab+2b2.
(1)由图 可得等式 a2+b2+c2+2ab+2bc+2ac .
(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)图 中给出了边长分别为a,b的小正方形纸片和长、宽分别为b,a的长方形纸片,现有足量的这三种纸片.
①请你用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,仿照图 、图 画出拼法并标注a,b;
②研究①中拼图发现,因式分解2a2+5ab+2b2的结果为 (a+2b)(2a+b) .
【解答】解:(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
故答案为:a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2﹣2(ab+bc+ac)=121﹣76=45;
(3)①根据题意,作出图形如下(答案不唯一):
②(a+2b)(2a+b)
24.(8分)阅读下列材料:
提取公因式法、公式法是初中阶段最常用分解因式的方法,但有些多项式只单纯用上述方法就无法分解,如x2﹣2xy+y2﹣16,我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解,过程如下:
x2﹣2xy+y2﹣16=(x﹣y)2﹣16=(x﹣y+4)(x﹣y﹣4)
这种分解因式的方法叫“分组分解法”.利用这种分组的思想方法解决下列问题:
(1)分解因式:x2﹣9y2﹣2x+6y;
(2)分解因式:x4﹣3x2y2+2y4;
(3)请比较多项式2x2﹣5xy+3y2﹣4y+4与x2﹣xy﹣2y2﹣2y﹣1的大小,并说明理由.
【解答】解:(1)原式=(x+3y)(x﹣3y)﹣2(x﹣3y)
=(x﹣3y)(x+3y﹣2);
(2)原式=x4﹣x2y2﹣2x2y2+2y4
=x2(x2﹣y2)﹣2y2(x2﹣y2)
=((x2﹣y2)(x2﹣2y2)
=(x+y)(x﹣y)(x2﹣2y2);
(3)2x2﹣5xy+3y2﹣4y+4>x2﹣xy﹣2y2﹣2y﹣1.理由如下:
∵(2x2﹣5xy+3y2﹣4y+4)﹣(x2﹣xy﹣2y2﹣2y﹣1)
=2x2﹣5xy+3y2﹣4y+4﹣x2+xy+2y2+2y+1
=x2﹣4xy+5y2﹣2y+5
=x2﹣4xy+4y2+y2﹣2y+1+4
=(x﹣2y)2+(y﹣1)2+4>0,
∴2x2﹣5xy+3y2﹣4y+4>x2﹣xy﹣2y2﹣2y﹣1.
第1页(共3页)
一、选择题(每小题3分,共30分)
1.(3分)下列因式分解正确的是( )
A.x2﹣x=x(x+1) B.a2﹣3a﹣4=(a+4)(a﹣1)
C.a2+2ab﹣b2=(a﹣b)2 D.x2﹣y2=(x+y)(x﹣y)
2.(3分)把a2x+ay﹣a3xy因式分解时,应提取的公因式是( )
A.a2 B.a C.ax D.ay
3.(3分)下列各式能够用完全平方公式因式分解的是( )
A.4x2+1 B.4x2+4x+1 C.4x2+4x﹣1 D.4x2﹣4x﹣1
4.(3分)王老师布置了5道因式分解的题,小明同学的答案如下,你认为他做对的题的序号是( )
①1+4x2=(1+2x)2;②6xyz﹣8xy2=2xyz(3﹣4y);③4x+2y﹣6z=2(2x+y﹣3z);④a2﹣2ab+b2=(a﹣b)2;⑤x2y﹣4y=y(x2﹣4).
A.①② B.③④ C.④⑤ D.②③④⑤
5.(3分)将下列多项式因式分解,结果中不含有因式a+1的是( )
A.a2﹣1 B.a2+a
C.a2+a﹣2 D.(a+2)2﹣2(a+2)+1
6.(3分)若关于x的二次三项式x2﹣kx﹣b因式分解为(x﹣1)(x﹣3),则k+b的值为( )
A.﹣1 B.1 C.﹣7 D.7
7.(3分)在探索因式分解的公式时,可以借助几何图形来解释某些公式.如图,从左图到右图的变化过程中,解释的因式分解公式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.a2﹣b2=(a+b)(a﹣b)
C.a2+b2=(a+b)2 D.(a﹣b)2=a2﹣2ab+b2
8.(3分)若+q2﹣8q+16=0,则因式分解(x2+y2)﹣(pxy+q)的结果是( )
A.(x﹣y)2﹣4 B.(x﹣y﹣2)(x﹣y+2)
C.(x﹣y+2)2 D.(x+y﹣2)(x+y+2)
9.(3分)要在二次三项式x2+□x﹣6的□中填上一个整数,使它能按x2+(a+b)x+ab型分解为(x+a)(x+b)的形式,那么这些数只能是( )
A.1,﹣1 B.5,﹣5
C.1,﹣1,5,﹣5 D.以上答案都不对
10.(3分)已知三个实数a,b,c满足a﹣2b+c=0,a+2b+c<0,则( )
A.b>0,b2﹣ac≤0 B.b<0,b2﹣ac≤0
C.b>0,b2﹣ac≥0 D.b<0,b2﹣ac≥0
二、填空题(每小题3分,共18分)
11.(3分)已知a2+a=0,则2a2+2a+2021= .
12.(3分)有下列各组代数式:①5a﹣5b和5a+5b;②ax+y和x+ay;③a3+2a2b+ab2和a2+ab;④x2﹣4y2和2xy+y2.其中没有公因式的是 (只填序号).
13.(3分)已知关于x的代数式x2﹣(a+1)x+9是完全平方式,则a= .
14.(3分)为了烘托新年的节日氛围,市政部门在某广场上用鲜花摆放了一个圆形花坛.已知该花坛的面积为(πa2+18πab+81πb2)平方米(a>0,b>0),则这个圆形花坛的半径为 米.
15.(3分)在完成因式分解的练习时,小明不小心将一道题4x3弄上了污渍,他只记得将这个多项式因式分解时应先提公因式,再用平方差公式分解,请你帮小明想一想,老师布置的原题可能是 ,因式分解的结果是 .(填一个合适的即可)
16.(3分)如图,甲类纸片是边长为x的正方形,乙类纸片是边长为y的正方形,丙类纸片是长、宽分别为x和y的长方形.现有甲类纸片1张,乙类纸片4张,则应取 张丙类纸片,才能用它们拼成一个新的正方形,拼成的正方形的边长为 .
三、解答题(共52分)
17.(6分)把下列各式因式分解:
(1)(a+b)2+a+b+;
(2)8(x2﹣2y2)﹣x(7x+y)+xy.
18.(6分)用简便方法计算:
(1)﹣23.7×+×1.3﹣2.6×;
(2)2020+20202﹣20212.
19.(6分)如图,边长为a,b的长方形,它的周长为14,面积为10,求下列各式的值:
(1)a2b+ab2;
(2)a2+b2+ab
20.(6分)先分解因式,再求值:
(1)15a2(b+4)﹣30a(b+4),其中a=2,b=﹣2;
(2)(x2+y2)2﹣4x2y2,其中x=3.5,y=1.5.
21.(6分)已知a、b、c分别是△ABC的三边.
(1)分别将多项式a2c2﹣b2c2,a4﹣b4进行因式分解,
(2)若a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状,并说明理由.
22.(6分)完全平方公式是初中数学的重要公式之一:(a+b)2=a2+2ab+b2,完全平方公式既可以用来进行整式计算又可以用来进行分解因式.
发现:3+2=2+2+1=()2+2+12=(+1)2;
应用:
(1)写出一个能用上面方法进行因式分解的式子,并进行因式分解;
(2)若a+b=(m+n)2,请用m,n表示a,b.
拓展:如图在Rt△ABC中,BC=1,AC=,∠C=90°,延长CA至点D,使AD=AB,求BD的长.(参考上面提供的方法把结果进行化简)
23.(8分)阅读材料并解决问题.
把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如:由图 可得等式(a+2b)(a+b)=a2+3ab+2b2.
(1)由图 可得等式 .
(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)图 中给出了边长分别为a,b的小正方形纸片和长、宽分别为b,a的长方形纸片,现有足量的这三种纸片.
①请你用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,仿照图 、图 画出拼法并标注a,b;
②研究①中拼图发现,因式分解2a2+5ab+2b2的结果为 .
24.(8分)阅读下列材料:
提取公因式法、公式法是初中阶段最常用分解因式的方法,但有些多项式只单纯用上述方法就无法分解,如x2﹣2xy+y2﹣16,我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解,过程如下:
x2﹣2xy+y2﹣16=(x﹣y)2﹣16=(x﹣y+4)(x﹣y﹣4)
这种分解因式的方法叫“分组分解法”.利用这种分组的思想方法解决下列问题:
(1)分解因式:x2﹣9y2﹣2x+6y;
(2)分解因式:x4﹣3x2y2+2y4;
(3)请比较多项式2x2﹣5xy+3y2﹣4y+4与x2﹣xy﹣2y2﹣2y﹣1的大小,并说明理由.
北师大新版八年级下册《第4章 因式分解》单元测试卷(2)
参考答案与试题解析
一、选择题(每小题3分,共30分)
1.(3分)下列因式分解正确的是( )
A.x2﹣x=x(x+1) B.a2﹣3a﹣4=(a+4)(a﹣1)
C.a2+2ab﹣b2=(a﹣b)2 D.x2﹣y2=(x+y)(x﹣y)
【解答】解:A、原式=x(x﹣1),错误;
B、原式=(a﹣4)(a+1),错误;
C、a2+2ab﹣b2,不能分解因式,错误;
D、原式=(x+y)(x﹣y),正确.
故选:D.
2.(3分)把a2x+ay﹣a3xy因式分解时,应提取的公因式是( )
A.a2 B.a C.ax D.ay
【解答】解:把a2x+ay﹣a3xy因式分解时,应提取的公因式是a.
故选:B.
3.(3分)下列各式能够用完全平方公式因式分解的是( )
A.4x2+1 B.4x2+4x+1 C.4x2+4x﹣1 D.4x2﹣4x﹣1
【解答】解:A、4x2+1,不符合完全平方公式的特征,不合题意;
B、4x2+4x+1=(2x+1)2,符合完全平方公式的特征,符合题意;
C、4x2+4x﹣1,不符合完全平方公式的特征,不合题意;
D、4x2﹣4x﹣1,不符合完全平方公式的特征,不合题意;
故选:B.
4.(3分)王老师布置了5道因式分解的题,小明同学的答案如下,你认为他做对的题的序号是( )
①1+4x2=(1+2x)2;②6xyz﹣8xy2=2xyz(3﹣4y);③4x+2y﹣6z=2(2x+y﹣3z);④a2﹣2ab+b2=(a﹣b)2;⑤x2y﹣4y=y(x2﹣4).
A.①② B.③④ C.④⑤ D.②③④⑤
【解答】解:①1+4x2,不符合完全平方公式的特征,不能分解因式,故①错误;
②6xyz﹣8xy2=2xy(3z﹣4y),故②错误;
③4x+2y﹣6z=2(2x+y﹣3z),故③正确;
④a2﹣2ab+b2=(a﹣b)2,故④正确;
⑤x2y﹣4y=y(x2﹣4)=y(x+2)(x﹣2)故⑤错误.
故选:B.
5.(3分)将下列多项式因式分解,结果中不含有因式a+1的是( )
A.a2﹣1 B.a2+a
C.a2+a﹣2 D.(a+2)2﹣2(a+2)+1
【解答】解:∵a2﹣1=(a+1)(a﹣1),
a2+a=a(a+1),
a2+a﹣2=(a+2)(a﹣1),
(a+2)2﹣2(a+2)+1=(a+2﹣1)2=(a+1)2,
∴结果中不含有因式a+1的是选项C;
故选:C.
6.(3分)若关于x的二次三项式x2﹣kx﹣b因式分解为(x﹣1)(x﹣3),则k+b的值为( )
A.﹣1 B.1 C.﹣7 D.7
【解答】解:根据题意得:x2﹣kx﹣b=(x﹣1)(x﹣3)=x2﹣4x+3,
∴k=4,b=﹣3,
则k+b=1,
故选:B.
7.(3分)在探索因式分解的公式时,可以借助几何图形来解释某些公式.如图,从左图到右图的变化过程中,解释的因式分解公式是( )
A.(a+b)(a﹣b)=a2﹣b2 B.a2﹣b2=(a+b)(a﹣b)
C.a2+b2=(a+b)2 D.(a﹣b)2=a2﹣2ab+b2
【解答】解:如图,从左图到右图的变化过程中,解释的因式分解公式是:a2﹣b2=(a+b)(a﹣b),
故选:B.
8.(3分)若+q2﹣8q+16=0,则因式分解(x2+y2)﹣(pxy+q)的结果是( )
A.(x﹣y)2﹣4 B.(x﹣y﹣2)(x﹣y+2)
C.(x﹣y+2)2 D.(x+y﹣2)(x+y+2)
【解答】解:∵+q2﹣8q+16=0,
∴+(q﹣4)2=0,
∴p﹣2=0,q﹣4=0,
解得p=2,q=4,
∴(x2+y2)﹣(pxy+q)
=(x2+y2)﹣(2xy+4)
=(x2+y2﹣2xy)﹣4
=(x﹣y)2﹣4
=(x﹣y+2)(x﹣y﹣2).
故选:B.
9.(3分)要在二次三项式x2+□x﹣6的□中填上一个整数,使它能按x2+(a+b)x+ab型分解为(x+a)(x+b)的形式,那么这些数只能是( )
A.1,﹣1 B.5,﹣5
C.1,﹣1,5,﹣5 D.以上答案都不对
【解答】解:﹣6可以分成:﹣2×3,2×(﹣3),﹣1×6,1×(﹣6),
□中填上的整数应该是﹣6的两个因数的和,即1,﹣1,5,﹣5.
故选:C.
10.(3分)已知三个实数a,b,c满足a﹣2b+c=0,a+2b+c<0,则( )
A.b>0,b2﹣ac≤0 B.b<0,b2﹣ac≤0
C.b>0,b2﹣ac≥0 D.b<0,b2﹣ac≥0
【解答】解:∵a﹣2b+c=0,a+2b+c<0,
∴a+c=2b,b=,
∴a+2b+c=(a+c)+2b=4b<0,
∴b<0,
∴b2﹣ac==﹣ac==≥0,
即b<0,b2﹣ac≥0,
故选:D.
二、填空题(每小题3分,共18分)
11.(3分)已知a2+a=0,则2a2+2a+2021= 2021 .
【解答】解:∵a2+a=0,
∴2a2+2a+2021
=2(a2+a)+2021
=2×0+2021
=0+2021
=2021.
故答案为:2021.
12.(3分)有下列各组代数式:①5a﹣5b和5a+5b;②ax+y和x+ay;③a3+2a2b+ab2和a2+ab;④x2﹣4y2和2xy+y2.其中没有公因式的是 ②④ (只填序号).
【解答】解:①5a﹣5b和5a+5b有公因式,公因式为5;
②ax+y和x+ay没有公因式;
③a3+2a2b+ab2和a2+ab有公因式,公因式为a(a+b);
④x2﹣4y2和2xy+y2没有公因式.
没有公因式的是②④.
故答案为:②④.
13.(3分)已知关于x的代数式x2﹣(a+1)x+9是完全平方式,则a= 5或﹣7 .
【解答】解:∵关于x的代数式x2﹣(a+1)x+9是完全平方式,
∴x2﹣(a+1)x+32=(x±3)2,
∴a+1=±6,
解得:a=5或a=﹣7.
故答案为:5或﹣7.
14.(3分)为了烘托新年的节日氛围,市政部门在某广场上用鲜花摆放了一个圆形花坛.已知该花坛的面积为(πa2+18πab+81πb2)平方米(a>0,b>0),则这个圆形花坛的半径为 (a+9b) 米.
【解答】解:∵πa2+18πab+81πb2
=π(a2+18ab+81b2)
=π(a+9b)2
=πr2,
∴r=a+9b,
故答案为:(a+9b).
15.(3分)在完成因式分解的练习时,小明不小心将一道题4x3弄上了污渍,他只记得将这个多项式因式分解时应先提公因式,再用平方差公式分解,请你帮小明想一想,老师布置的原题可能是 4x3﹣9x(答案不唯一) ,因式分解的结果是 x(2x+3)(2x﹣3) .(填一个合适的即可)
【解答】解:老师布置的题目可能是4x3﹣9x(答案不唯一),
其因式分解的结果为:4x3﹣9x=x(4x2﹣9)=x(2x+3)(2x﹣3),
故答案为:4x3﹣9x(答案不唯一),x(2x+3)(2x﹣3).
16.(3分)如图,甲类纸片是边长为x的正方形,乙类纸片是边长为y的正方形,丙类纸片是长、宽分别为x和y的长方形.现有甲类纸片1张,乙类纸片4张,则应取 4 张丙类纸片,才能用它们拼成一个新的正方形,拼成的正方形的边长为 x+2y .
【解答】解:甲类纸片1张,面积为x2;乙类纸片4张,面积为4y2.
设至少取丙类纸片a张才能用它们拼成一个新的正方形,
∵x2+4y2+axy是一个完全平方式,
∴a应取4,
即丙类纸片应取4张.
∵x2+4y2+4xy=(x+2y)2,
∴拼成的正方形的边长为x+2y.
故答案为:4,x+2y.
三、解答题(共52分)
17.(6分)把下列各式因式分解:
(1)(a+b)2+a+b+;
(2)8(x2﹣2y2)﹣x(7x+y)+xy.
【解答】解:(1)原式=(a+b+)2.
(2)8(x2﹣2y2)﹣x(7x+y)+xy
=8x2﹣16y2﹣7x2﹣xy+xy
=x2﹣16y2
=(x+4y)(x﹣4y).
18.(6分)用简便方法计算:
(1)﹣23.7×+×1.3﹣2.6×;
(2)2020+20202﹣20212.
【解答】解:(1)原式=×(﹣23.7+1.3﹣2.6)
=×(﹣25)
=﹣20.
(2)原式=2020﹣(20212﹣20202)
=2020﹣(2021+2020)×(2021﹣2020)
=2020﹣2021﹣2020
=﹣2021.
19.(6分)如图,边长为a,b的长方形,它的周长为14,面积为10,求下列各式的值:
(1)a2b+ab2;
(2)a2+b2+ab
【解答】解:(1)∵a+b=7,ab=10,
∴a2b+ab2=ab(a+b)=70;
(2)a2+b2=(a+b)2﹣2ab=72﹣2×10=29,
∴a2+b2+ab=29+10=39.
20.(6分)先分解因式,再求值:
(1)15a2(b+4)﹣30a(b+4),其中a=2,b=﹣2;
(2)(x2+y2)2﹣4x2y2,其中x=3.5,y=1.5.
【解答】解:(1)原式=15a(b+4)(a﹣2)
当a=2,b=﹣2时,
原式=15×2×(﹣2+4)×(2﹣2)=0;
(2)原式=(x2+2xy+y2)(x2﹣2xy+y2)
=(x+y)2(x﹣y)2
当x=3.5,y=1.5时,
原式=(3.5+1.5)2×(3.5﹣1.5)2=100.
21.(6分)已知a、b、c分别是△ABC的三边.
(1)分别将多项式a2c2﹣b2c2,a4﹣b4进行因式分解,
(2)若a2c2﹣b2c2=a4﹣b4,试判断△ABC的形状,并说明理由.
【解答】解:(1)a2c2﹣b2c2=c2(a2﹣b2)=c2(a+b)(a﹣b);
a4﹣b4=(a2﹣b2)(a2+b2)=(a﹣b)(a+b)(a2+b2);
(2)∵a2c2﹣b2c2=a4﹣b4,
∴c2(a+b)(a﹣b)=(a﹣b)(a+b)(a2+b2);
∴c2(a+b)(a﹣b)﹣(a﹣b)(a+b)(a2+b2)=0;
∴(a+b)(a﹣b)(c2﹣a2﹣b2)=0,
∵a、b、c分别是△ABC的三边.
∴a﹣b=0或c2﹣a2﹣b2=0,
∴a=b或c2=a2+b2,
∴△ABC为等腰三角形或直角三角形.
22.(6分)完全平方公式是初中数学的重要公式之一:(a+b)2=a2+2ab+b2,完全平方公式既可以用来进行整式计算又可以用来进行分解因式.
发现:3+2=2+2+1=()2+2+12=(+1)2;
应用:
(1)写出一个能用上面方法进行因式分解的式子,并进行因式分解;
(2)若a+b=(m+n)2,请用m,n表示a,b.
拓展:如图在Rt△ABC中,BC=1,AC=,∠C=90°,延长CA至点D,使AD=AB,求BD的长.(参考上面提供的方法把结果进行化简)
【解答】解:(1)4+2=3+2+1=;
(2)∵a+b=(m+n)2,
∴a+b=m2+2n2+2mn,
∴a=m2+2n2,b=2mn;
拓展:由题意得,AB=,
∴AD=AB=2,
∴CD=+2,
∴BD2=BC2+CD2=1+=6+4+2==,
∴BD=.
23.(8分)阅读材料并解决问题.
把几个图形拼成一个新的图形,再通过两种不同的方式计算同一个图形的面积,可以得到一个等式,也可以求出一些不规则图形的面积.
例如:由图 可得等式(a+2b)(a+b)=a2+3ab+2b2.
(1)由图 可得等式 a2+b2+c2+2ab+2bc+2ac .
(2)利用(1)所得等式,解决问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值.
(3)图 中给出了边长分别为a,b的小正方形纸片和长、宽分别为b,a的长方形纸片,现有足量的这三种纸片.
①请你用所给的纸片拼出一个面积为2a2+5ab+2b2的长方形,仿照图 、图 画出拼法并标注a,b;
②研究①中拼图发现,因式分解2a2+5ab+2b2的结果为 (a+2b)(2a+b) .
【解答】解:(1)(a+b+c)2=a2+b2+c2+2ab+2bc+2ac,
故答案为:a2+b2+c2+2ab+2bc+2ac;
(2)∵a+b+c=11,ab+bc+ac=38,
∴a2+b2+c2=(a+b+c)2﹣2(ab+bc+ac)=121﹣76=45;
(3)①根据题意,作出图形如下(答案不唯一):
②(a+2b)(2a+b)
24.(8分)阅读下列材料:
提取公因式法、公式法是初中阶段最常用分解因式的方法,但有些多项式只单纯用上述方法就无法分解,如x2﹣2xy+y2﹣16,我们细心观察这个式子就会发现,前三项符合完全平方公式,进行变形后可以与第四项结合再运用平方差公式进行分解,过程如下:
x2﹣2xy+y2﹣16=(x﹣y)2﹣16=(x﹣y+4)(x﹣y﹣4)
这种分解因式的方法叫“分组分解法”.利用这种分组的思想方法解决下列问题:
(1)分解因式:x2﹣9y2﹣2x+6y;
(2)分解因式:x4﹣3x2y2+2y4;
(3)请比较多项式2x2﹣5xy+3y2﹣4y+4与x2﹣xy﹣2y2﹣2y﹣1的大小,并说明理由.
【解答】解:(1)原式=(x+3y)(x﹣3y)﹣2(x﹣3y)
=(x﹣3y)(x+3y﹣2);
(2)原式=x4﹣x2y2﹣2x2y2+2y4
=x2(x2﹣y2)﹣2y2(x2﹣y2)
=((x2﹣y2)(x2﹣2y2)
=(x+y)(x﹣y)(x2﹣2y2);
(3)2x2﹣5xy+3y2﹣4y+4>x2﹣xy﹣2y2﹣2y﹣1.理由如下:
∵(2x2﹣5xy+3y2﹣4y+4)﹣(x2﹣xy﹣2y2﹣2y﹣1)
=2x2﹣5xy+3y2﹣4y+4﹣x2+xy+2y2+2y+1
=x2﹣4xy+5y2﹣2y+5
=x2﹣4xy+4y2+y2﹣2y+1+4
=(x﹣2y)2+(y﹣1)2+4>0,
∴2x2﹣5xy+3y2﹣4y+4>x2﹣xy﹣2y2﹣2y﹣1.
第1页(共3页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
