苏科版数学七下10.4用二元一次方程组解决问题 习题课件(共25张PPT)
文档属性
| 名称 | 苏科版数学七下10.4用二元一次方程组解决问题 习题课件(共25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 443.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 00:00:00 | ||
图片预览







文档简介
(共25张PPT)
初 一 数 学
10.5“二元一次方程组的应用”
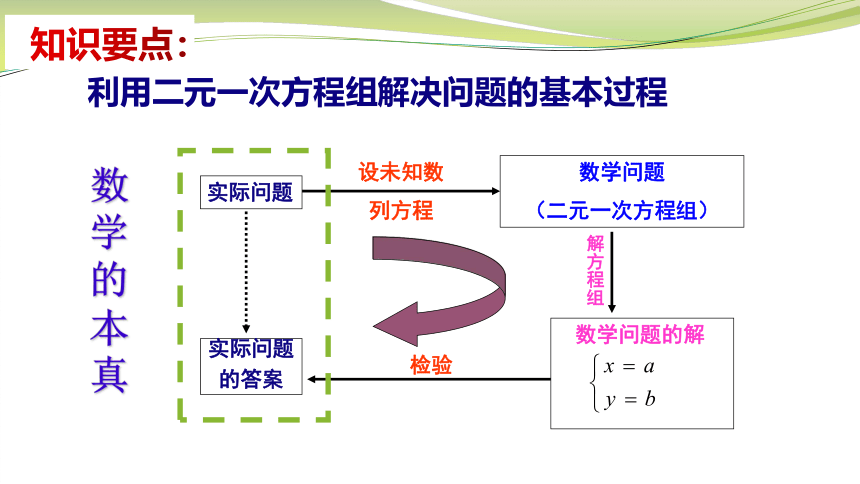
利用二元一次方程组解决问题的基本过程
实际问题
实际问题
的答案
数学问题
(二元一次方程组)
设未知数
列方程
数学问题的解
解方程组
检验
知识要点:
数学的本真
知识要点:
审 设 列 解 验 答
弄清题目中已知、未知间的两个等量关系;
列出方程组;
分析题意,根据两个等量关系
解此方程组,求出未知数的值;
检验求得的值是否正确和符合实际情形;
写出答案。
列方程组解应用题的一般步骤:
设出两个未知数(一般设直接未知数);
1.用一根长80cm的绳子围成一个长方形,且这个长方形的长比宽多10cm.设这个长方形的长为xcm、宽为ycm,列出关于x、y的二元一次方程组,下列正确的是( )
A. B. C. D.
提示:这个长方形的长为xcm、宽为ycm,
由“这个长方形的长比宽多10cm”得到方程:x﹣y=10.
由长方形的周长是80cm得到方程:2x+2y=80.
所以由题意可得方程组:
B
基础练习:
双基练习
C
基础练习:
2.
含有百分数的方程组怎么解呢?
双基练习
6.1万元、6.9万元
要注意单位统一!
基础练习:
3.
A
双基练习
基础练习:
4.
关注一下方程组的解法!
双基练习
A
基础练习:
5.
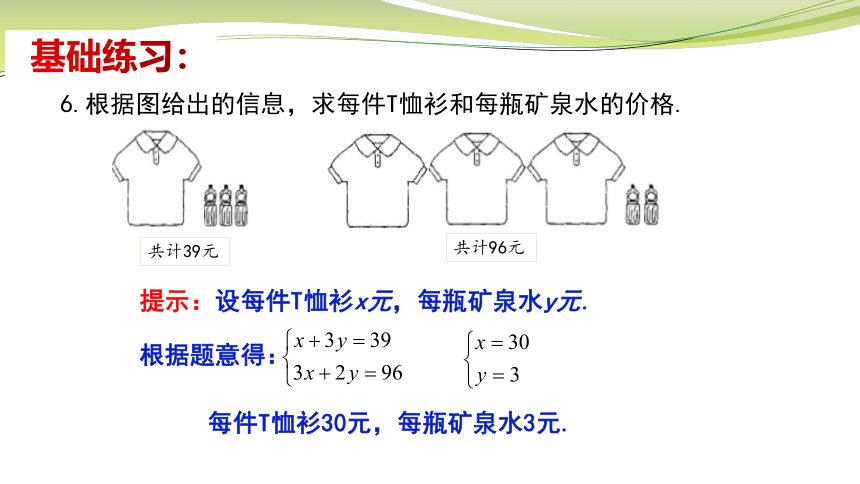
6.根据图给出的信息,求每件T恤衫和每瓶矿泉水的价格.
基础练习:
提示:设每件T恤衫x元,每瓶矿泉水y元.
根据题意得:
共计39元
共计96元
每件T恤衫30元,每瓶矿泉水3元.
例1.《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 类似地,图2所示的算筹图我们可以表述为( )
图2
图1
A. B.
C. D.
例题赏析:
A
例2.小亮在匀速行驶的汽车里,注意到公路里程碑上的数是两位数;1h后看到里程碑上的数与第一次看到的两位数恰好颠倒了数字顺序;再过1h后,第三次看到的里程碑上的数字又恰好是第一次见到的数字的两位数的数字之间添加一个0的三位数,这3块里程碑上的数各是多少?
解:设首次见到的两位数的十位数字为x,个位数字为 y.
则:第1次:10x+y, 第2次:10y+x, 第3次:100x+y
例题赏析:
1≤x≤9,1≤y≤9
根据题意得:10y+x-(10x+y)=100x+y-(10y+x)
解得y=6x
∴ x=1,y=6
里程碑上的三个数是:第1次为16, 第2次为61, 第3次为106
汽车的速度多少?
例3.七年级(2)班的一个综合实践活动小组去 A、B两个超市调查去年和今年春节期间的销售情况,下图是调查后小敏与其他两位同学进行交流的情景,根据他们的对话,请你分别求出A、B两个超市今年春节期间的销售额.
两超市销售额去年共为150万元,今年共为170万元.
A超市销售额今年比去年增加15%.
B超市销售额今年比去年增加10%.
设A超市去年销售额为x万元,B超市去年销售额为y万元。
去年: x+y=150
今年:(1+15%)x+(1+10%)y=170
例题赏析:
答:A超市今年是115万元;B超市今年是55万元。
解:设A超市去年销售额为x万元,B超市去年销售额为y万元。
解得 x=100
y=50
根据题意,得
x+y=150
x(1+15%)+y(1+10%)=170
那么x(1+15%)=115 y(1+10%)=55
例题赏析:
如果设今年的销售额呢?
例4.某铁路桥长1000m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.求火车的速度和长度.
例题赏析:
行程=桥长+火车长
行程=桥长﹣火车长
火车60s内所行路程=桥长+火车长
火车40s内所行路程=桥长-火车长
例4.某铁路桥长1000m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.求火车的速度和长度.
例题赏析:
解:设火车的速度为x m/s, 火车的长为y m ,
根据题意,得:
答:火车的速度为20 m/s,设火车的长为200 m.
解这个方程组得:
例题赏析:
例5.泰华商场到厂家选购A,B两种型号的服装,若购进A种型号服装3件,B种型号服装2件,需要470元;若购进A种型号服装9件,B种型号服装10件,需要1810元.
(1)求A,B两种型号的服装每件进价分别为多少元?
解:(1)设A型服装每件进价x元,B型服装每件进价y元,
根据题意可得
解得
答:A,B两种型号的服装每件进价分别为90、100元;
例题赏析:
例题赏析:
(2)若销售1件A型服装每件可获利18元,销售一件B型服装可获利30元,根据市场需求,商场决定,购进A型服装的数量要比购进B型服装的数量的2倍还要多4件,且A型服装最多可购进28件,这样服装全部售出后,可使总获利不少于798元,问有几种进货方案
(2)设销售A种服装的件数为a件,B种服装的件数为b件.
根据题意,得 18a+30b≥798
a=2b+4
而a≤28,可得b≤12
解得 b ≥11
因此11≤b≤12
有两种进货方案:A型26件,B型11件;A型28件,B型12件
1.甲、乙两仓库共存粮500t,现在从甲仓运出粮食的50%,从乙仓运出粮食的40%,结果乙仓库所余的粮食比甲仓库多80t,求甲、乙两仓库原来的粮食数量?
尝试练习:
2.甲、乙两地之间路程为20km,A,B两人同时相对而行,2小时后相遇,相遇后A就返回甲地,B仍向甲地前进,A回到甲地时,B离甲地还有2km,求A,B两人速度.
或
尝试练习:
3.小虎、大壮和明明三人玩飞镖游戏,各投5支镖,规定在同一环内得分相同,中靶和得分情况如图,求大壮的得分多少?
尝试练习:
4.《九章算术》第七卷“盈不足"中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何 ”译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少 ”
尝试练习:
尝试练习:
5.苏州乐园的价格规定如下表,我校七年级(1)、(2)两个共104人去游乐园,其中(1)班人数不足50人,(2)班人数超过50人,经估算,如果两班都以班为单位分别购票,则一共应付1240元;问两班各有多少名学生 如果两班联合起来,作为一个团体购票,则可以节省多少钱?
1、静心读题,跳出情境,弄清题意;标出关键的词语和句子,让题意清晰简单化,找出题中等量关系;
列方程(组)解应用题时务必注意:
2、设未知数后,根据关键的句子,用未知数的代数式表示相关的量,再根据等量关系得到方程(组)。
学习有方法,解题有技巧.
初 一 数 学
10.5“二元一次方程组的应用”
利用二元一次方程组解决问题的基本过程
实际问题
实际问题
的答案
数学问题
(二元一次方程组)
设未知数
列方程
数学问题的解
解方程组
检验
知识要点:
数学的本真
知识要点:
审 设 列 解 验 答
弄清题目中已知、未知间的两个等量关系;
列出方程组;
分析题意,根据两个等量关系
解此方程组,求出未知数的值;
检验求得的值是否正确和符合实际情形;
写出答案。
列方程组解应用题的一般步骤:
设出两个未知数(一般设直接未知数);
1.用一根长80cm的绳子围成一个长方形,且这个长方形的长比宽多10cm.设这个长方形的长为xcm、宽为ycm,列出关于x、y的二元一次方程组,下列正确的是( )
A. B. C. D.
提示:这个长方形的长为xcm、宽为ycm,
由“这个长方形的长比宽多10cm”得到方程:x﹣y=10.
由长方形的周长是80cm得到方程:2x+2y=80.
所以由题意可得方程组:
B
基础练习:
双基练习
C
基础练习:
2.
含有百分数的方程组怎么解呢?
双基练习
6.1万元、6.9万元
要注意单位统一!
基础练习:
3.
A
双基练习
基础练习:
4.
关注一下方程组的解法!
双基练习
A
基础练习:
5.
6.根据图给出的信息,求每件T恤衫和每瓶矿泉水的价格.
基础练习:
提示:设每件T恤衫x元,每瓶矿泉水y元.
根据题意得:
共计39元
共计96元
每件T恤衫30元,每瓶矿泉水3元.
例1.《九章算术》是我国东汉初年编订的一部数学经典著作.在它的“方程”一章里,一次方程组是由算筹布置而成的.《九章算术》中的算筹图是竖排的,为看图方便,我们把它改为横排,如图1、图2.图中各行从左到右列出的算筹数分别表示未知数x,y的系数与相应的常数项.把图1所示的算筹图用我们现在所熟悉的方程组形式表述出来,就是 类似地,图2所示的算筹图我们可以表述为( )
图2
图1
A. B.
C. D.
例题赏析:
A
例2.小亮在匀速行驶的汽车里,注意到公路里程碑上的数是两位数;1h后看到里程碑上的数与第一次看到的两位数恰好颠倒了数字顺序;再过1h后,第三次看到的里程碑上的数字又恰好是第一次见到的数字的两位数的数字之间添加一个0的三位数,这3块里程碑上的数各是多少?
解:设首次见到的两位数的十位数字为x,个位数字为 y.
则:第1次:10x+y, 第2次:10y+x, 第3次:100x+y
例题赏析:
1≤x≤9,1≤y≤9
根据题意得:10y+x-(10x+y)=100x+y-(10y+x)
解得y=6x
∴ x=1,y=6
里程碑上的三个数是:第1次为16, 第2次为61, 第3次为106
汽车的速度多少?
例3.七年级(2)班的一个综合实践活动小组去 A、B两个超市调查去年和今年春节期间的销售情况,下图是调查后小敏与其他两位同学进行交流的情景,根据他们的对话,请你分别求出A、B两个超市今年春节期间的销售额.
两超市销售额去年共为150万元,今年共为170万元.
A超市销售额今年比去年增加15%.
B超市销售额今年比去年增加10%.
设A超市去年销售额为x万元,B超市去年销售额为y万元。
去年: x+y=150
今年:(1+15%)x+(1+10%)y=170
例题赏析:
答:A超市今年是115万元;B超市今年是55万元。
解:设A超市去年销售额为x万元,B超市去年销售额为y万元。
解得 x=100
y=50
根据题意,得
x+y=150
x(1+15%)+y(1+10%)=170
那么x(1+15%)=115 y(1+10%)=55
例题赏析:
如果设今年的销售额呢?
例4.某铁路桥长1000m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.求火车的速度和长度.
例题赏析:
行程=桥长+火车长
行程=桥长﹣火车长
火车60s内所行路程=桥长+火车长
火车40s内所行路程=桥长-火车长
例4.某铁路桥长1000m,现有一列火车从桥上通过,测得该火车从开始上桥到完全过桥共用了1min,整列火车完全在桥上的时间共40s.求火车的速度和长度.
例题赏析:
解:设火车的速度为x m/s, 火车的长为y m ,
根据题意,得:
答:火车的速度为20 m/s,设火车的长为200 m.
解这个方程组得:
例题赏析:
例5.泰华商场到厂家选购A,B两种型号的服装,若购进A种型号服装3件,B种型号服装2件,需要470元;若购进A种型号服装9件,B种型号服装10件,需要1810元.
(1)求A,B两种型号的服装每件进价分别为多少元?
解:(1)设A型服装每件进价x元,B型服装每件进价y元,
根据题意可得
解得
答:A,B两种型号的服装每件进价分别为90、100元;
例题赏析:
例题赏析:
(2)若销售1件A型服装每件可获利18元,销售一件B型服装可获利30元,根据市场需求,商场决定,购进A型服装的数量要比购进B型服装的数量的2倍还要多4件,且A型服装最多可购进28件,这样服装全部售出后,可使总获利不少于798元,问有几种进货方案
(2)设销售A种服装的件数为a件,B种服装的件数为b件.
根据题意,得 18a+30b≥798
a=2b+4
而a≤28,可得b≤12
解得 b ≥11
因此11≤b≤12
有两种进货方案:A型26件,B型11件;A型28件,B型12件
1.甲、乙两仓库共存粮500t,现在从甲仓运出粮食的50%,从乙仓运出粮食的40%,结果乙仓库所余的粮食比甲仓库多80t,求甲、乙两仓库原来的粮食数量?
尝试练习:
2.甲、乙两地之间路程为20km,A,B两人同时相对而行,2小时后相遇,相遇后A就返回甲地,B仍向甲地前进,A回到甲地时,B离甲地还有2km,求A,B两人速度.
或
尝试练习:
3.小虎、大壮和明明三人玩飞镖游戏,各投5支镖,规定在同一环内得分相同,中靶和得分情况如图,求大壮的得分多少?
尝试练习:
4.《九章算术》第七卷“盈不足"中记载:“今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何 ”译为:“今有人合伙购物,每人出8钱,会多3钱;每人出7钱,又差4钱.问人数、物价各多少 ”
尝试练习:
尝试练习:
5.苏州乐园的价格规定如下表,我校七年级(1)、(2)两个共104人去游乐园,其中(1)班人数不足50人,(2)班人数超过50人,经估算,如果两班都以班为单位分别购票,则一共应付1240元;问两班各有多少名学生 如果两班联合起来,作为一个团体购票,则可以节省多少钱?
1、静心读题,跳出情境,弄清题意;标出关键的词语和句子,让题意清晰简单化,找出题中等量关系;
列方程(组)解应用题时务必注意:
2、设未知数后,根据关键的句子,用未知数的代数式表示相关的量,再根据等量关系得到方程(组)。
学习有方法,解题有技巧.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
