苏科版数学九上 1.4用一元二次方程解决问题(3) 课件(共15张PPT)
文档属性
| 名称 | 苏科版数学九上 1.4用一元二次方程解决问题(3) 课件(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
1.4 用一元二次方程解决问题3
用方程解决实际问题的基本步骤
实际问题
实际问题的答案
数学问题
数学问题的答案
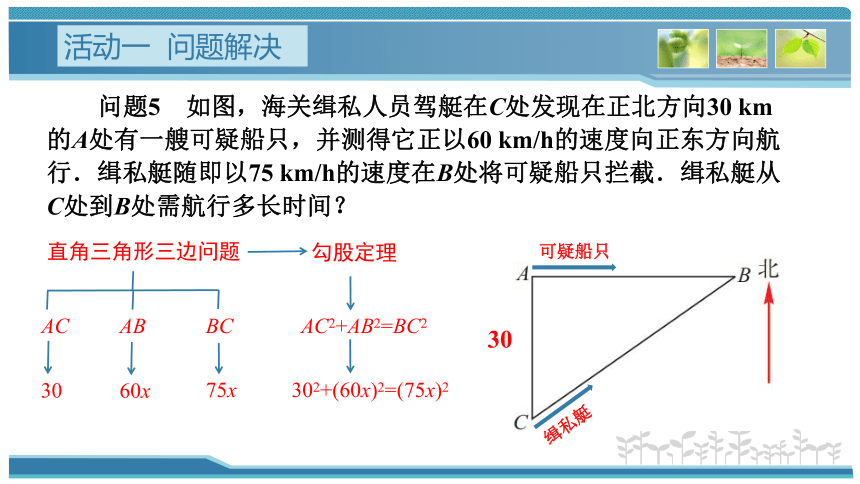
问题5 如图,海关缉私人员驾艇在C处发现在正北方向30 km的A处有一艘可疑船只,并测得它正以60 km/h的速度向正东方向航行.缉私艇随即以75 km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?
30
可疑船只
缉私艇
直角三角形三边问题
AC
AB
BC
30
60x
75x
AC2+AB2=BC2
302+(60x)2=(75x)2
勾股定理
活动一 问题解决
问题5 如图,海关缉私人员驾艇在C处发现在正北方向30 km的A处有一艘可疑船只,并测得它正以60 km/h的速度向正东方向航行.缉私艇随即以75 km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?
解:设缉私艇从C处到B处需航行x h,则AB=60x km,
BC=75x km.△ABC是直角三角形,AC=30 km.
于是(60x)2 + 30 2 =(75x) 2 .
解得x1= ,x 2 =- (舍去).
答:缉私艇从C处到B处需航行 h.
活动一 问题解决
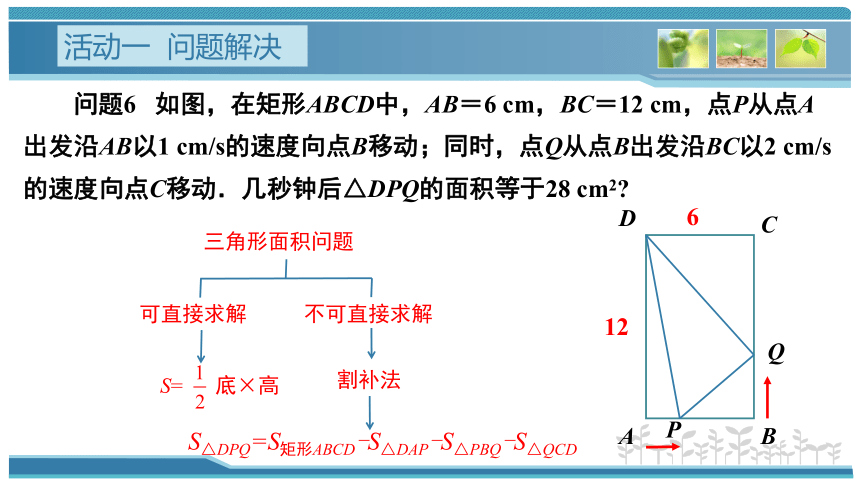
问题6 如图,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A出发沿AB以1 cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2 cm/s的速度向点C移动.几秒钟后△DPQ的面积等于28 cm2
A
B
C
D
P
Q
12
6
三角形面积问题
可直接求解
割补法
不可直接求解
S= 底×高
S△DPQ=S矩形ABCD-S△DAP-S△PBQ-S△QCD
活动一 问题解决
A
B
C
D
P
Q
12
6
x
6-x
2x
12-2x
S△DPQ=S矩形ABCD-S△DAP-S△PBQ-S△QCD
活动一 问题解决
解:设x秒后△DPQ的面积等于28 cm2.
根据题意,得
整理,得
解这个方程,得
答: 2秒或4秒后△DPQ的面积等于28 cm2.
活动一 问题解决
A
B
C
D
P
Q
12
6
x
6-x
2x
12-2x
再思考:
△DPQ的面积可以是58 cm2?
△DPQ可以是等腰三角形吗?
△DPQ可以是直角三角形吗?
活动一 问题解决
线段PQ长可以是 6 吗?
例1 如图,在一块长12米,宽8米的矩形空地上,修建同样宽的两条道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为60平方米,求道路的宽是多少米?
解:设道路的宽是x 米,则栽种花草的部分可合成一个两边长为(12﹣x)米和(8﹣x)米的矩形.
由题意得:(12﹣x)(8﹣x)=60,
整理得:x2﹣20x+36=0,
解得:x1=2,x2=18.
∵8﹣x>0,∴x<8,∴x=2.
答:道路的宽是2米.
活动二 灵活运用
8﹣x
12﹣x
解决有关面积问题时,除了直接运用面积公式计算外,还要会将不规则图形分割或组合成规则图形,并找出各部分图形面积之间的关系,再列方程求解.
(说明:上图中所有小路的宽度都相等)
转化
活动二 灵活运用
例2 如图所示,在Rt△ABC中.∠B=90°,AB=5 cm,BC=7 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,点Q从点B开始沿BC边向点C以2 cm/s的速度移动.当P、Q两点中有一点到达终点,则同时停止运动.
(1)如果P、Q分别从A、B同时出发,那么几秒后,△PBQ的面积为4 cm2?△PBQ的面积能否等于7 cm2?
解:(1)设x秒后,△BPQ的面积为4 cm2,
由 BP×BQ=4,得 (5﹣x)×2x=4,
整理得:x2﹣5x+4=0,
解得:x=1或x=4(舍去).
当x=4时,2x=8>7,舍去.
答:1秒后△BPQ的面积为4 cm2.
若 (5﹣x)×2x=7,整理得x2﹣5x+7=0,
∵b2﹣4ac=﹣3<0,∴方程没有实数根,
所以△BPQ的面积不可能等于7cm2.
活动二 灵活运用
2.如图所示,在Rt△ABC中.∠B=90°,AB=5 cm,BC=7 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,点Q从点B开始沿BC边向点C以2 cm/s的速度移动.当P、Q两点中有一点到达终点,则同时停止运动.
(2)如果P、Q分别从A、B同时出发,那么几秒后,PQ的长度等于5 cm.
解:由BP2+BQ2=52,
得(5﹣x)2+(2x)2=52,
整理得x2﹣2x=0,
解方程得:x=0(舍去),x=2.
答:2秒后PQ的长度等于5cm;
阅读分析题意,建立模型,列出方程
选择合适的方法求解数学问题
经过检验,找到符合题意的答案,解决实际问题
转化数学问题
1
求解数学问题
解决实际问题
课堂小结
实际问题
实际问题的解
数学模型
数学模型的解
验证
数学化
解
方
程
解释
数学建模
设未知数、列方程
祝同学们学习进步!
1.4 用一元二次方程解决问题3
用方程解决实际问题的基本步骤
实际问题
实际问题的答案
数学问题
数学问题的答案
问题5 如图,海关缉私人员驾艇在C处发现在正北方向30 km的A处有一艘可疑船只,并测得它正以60 km/h的速度向正东方向航行.缉私艇随即以75 km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?
30
可疑船只
缉私艇
直角三角形三边问题
AC
AB
BC
30
60x
75x
AC2+AB2=BC2
302+(60x)2=(75x)2
勾股定理
活动一 问题解决
问题5 如图,海关缉私人员驾艇在C处发现在正北方向30 km的A处有一艘可疑船只,并测得它正以60 km/h的速度向正东方向航行.缉私艇随即以75 km/h的速度在B处将可疑船只拦截.缉私艇从C处到B处需航行多长时间?
解:设缉私艇从C处到B处需航行x h,则AB=60x km,
BC=75x km.△ABC是直角三角形,AC=30 km.
于是(60x)2 + 30 2 =(75x) 2 .
解得x1= ,x 2 =- (舍去).
答:缉私艇从C处到B处需航行 h.
活动一 问题解决
问题6 如图,在矩形ABCD中,AB=6 cm,BC=12 cm,点P从点A出发沿AB以1 cm/s的速度向点B移动;同时,点Q从点B出发沿BC以2 cm/s的速度向点C移动.几秒钟后△DPQ的面积等于28 cm2
A
B
C
D
P
Q
12
6
三角形面积问题
可直接求解
割补法
不可直接求解
S= 底×高
S△DPQ=S矩形ABCD-S△DAP-S△PBQ-S△QCD
活动一 问题解决
A
B
C
D
P
Q
12
6
x
6-x
2x
12-2x
S△DPQ=S矩形ABCD-S△DAP-S△PBQ-S△QCD
活动一 问题解决
解:设x秒后△DPQ的面积等于28 cm2.
根据题意,得
整理,得
解这个方程,得
答: 2秒或4秒后△DPQ的面积等于28 cm2.
活动一 问题解决
A
B
C
D
P
Q
12
6
x
6-x
2x
12-2x
再思考:
△DPQ的面积可以是58 cm2?
△DPQ可以是等腰三角形吗?
△DPQ可以是直角三角形吗?
活动一 问题解决
线段PQ长可以是 6 吗?
例1 如图,在一块长12米,宽8米的矩形空地上,修建同样宽的两条道路(两条道路各与矩形的一条边平行),剩余部分栽种花草,且栽种花草的面积为60平方米,求道路的宽是多少米?
解:设道路的宽是x 米,则栽种花草的部分可合成一个两边长为(12﹣x)米和(8﹣x)米的矩形.
由题意得:(12﹣x)(8﹣x)=60,
整理得:x2﹣20x+36=0,
解得:x1=2,x2=18.
∵8﹣x>0,∴x<8,∴x=2.
答:道路的宽是2米.
活动二 灵活运用
8﹣x
12﹣x
解决有关面积问题时,除了直接运用面积公式计算外,还要会将不规则图形分割或组合成规则图形,并找出各部分图形面积之间的关系,再列方程求解.
(说明:上图中所有小路的宽度都相等)
转化
活动二 灵活运用
例2 如图所示,在Rt△ABC中.∠B=90°,AB=5 cm,BC=7 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,点Q从点B开始沿BC边向点C以2 cm/s的速度移动.当P、Q两点中有一点到达终点,则同时停止运动.
(1)如果P、Q分别从A、B同时出发,那么几秒后,△PBQ的面积为4 cm2?△PBQ的面积能否等于7 cm2?
解:(1)设x秒后,△BPQ的面积为4 cm2,
由 BP×BQ=4,得 (5﹣x)×2x=4,
整理得:x2﹣5x+4=0,
解得:x=1或x=4(舍去).
当x=4时,2x=8>7,舍去.
答:1秒后△BPQ的面积为4 cm2.
若 (5﹣x)×2x=7,整理得x2﹣5x+7=0,
∵b2﹣4ac=﹣3<0,∴方程没有实数根,
所以△BPQ的面积不可能等于7cm2.
活动二 灵活运用
2.如图所示,在Rt△ABC中.∠B=90°,AB=5 cm,BC=7 cm,点P从点A开始沿AB边向点B以1 cm/s的速度移动,点Q从点B开始沿BC边向点C以2 cm/s的速度移动.当P、Q两点中有一点到达终点,则同时停止运动.
(2)如果P、Q分别从A、B同时出发,那么几秒后,PQ的长度等于5 cm.
解:由BP2+BQ2=52,
得(5﹣x)2+(2x)2=52,
整理得x2﹣2x=0,
解方程得:x=0(舍去),x=2.
答:2秒后PQ的长度等于5cm;
阅读分析题意,建立模型,列出方程
选择合适的方法求解数学问题
经过检验,找到符合题意的答案,解决实际问题
转化数学问题
1
求解数学问题
解决实际问题
课堂小结
实际问题
实际问题的解
数学模型
数学模型的解
验证
数学化
解
方
程
解释
数学建模
设未知数、列方程
祝同学们学习进步!
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
