北师大版数学九年级下册2.2.3 二次函数的图象与性质 课件(共17张PPT)
文档属性
| 名称 | 北师大版数学九年级下册2.2.3 二次函数的图象与性质 课件(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 165.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 20:51:36 | ||
图片预览




文档简介
(共17张PPT)
第二章
2 二次函数的图象与性质
(第3课时)
知识回顾,问题引入
1.二次函数y=ax2+c的图象是什么形状的?
2.二次函数y=ax2+c的开口方向、对称轴、顶点坐标、增减性、最值分别是怎样的?
抛物线
分a>0和a<0两种情况
x -4 -3 -2 -1 0 1 2 3 4
2x2
2(x-1)2
32
0
32
50
18
18
8
8
2
0
2
18
8
2
2
8
18
32
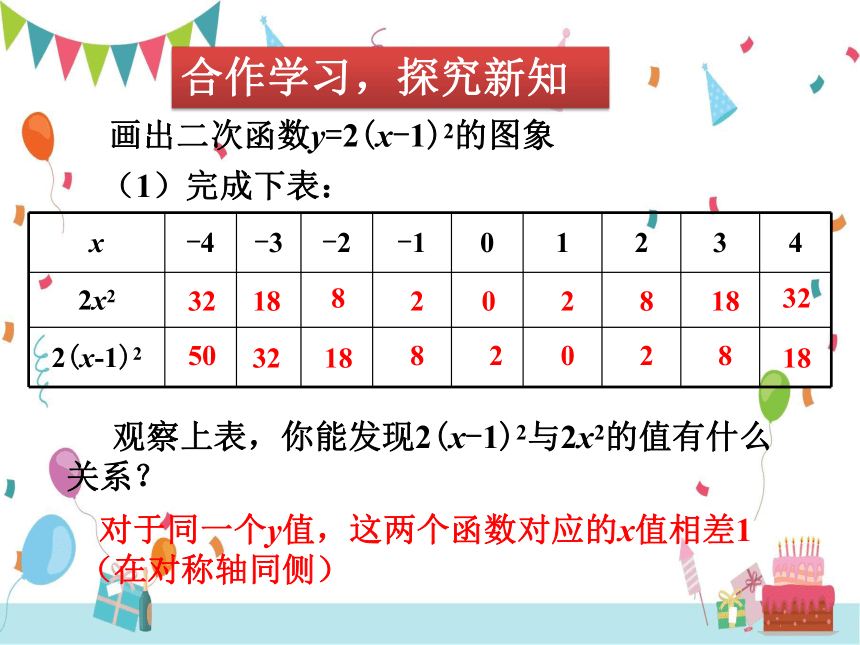
对于同一个y值,这两个函数对应的x值相差1(在对称轴同侧)
合作学习,探究新知
画出二次函数y=2(x-1)2的图象
(1)完成下表:
观察上表,你能发现2(x-1)2与2x2的值有什么关系?
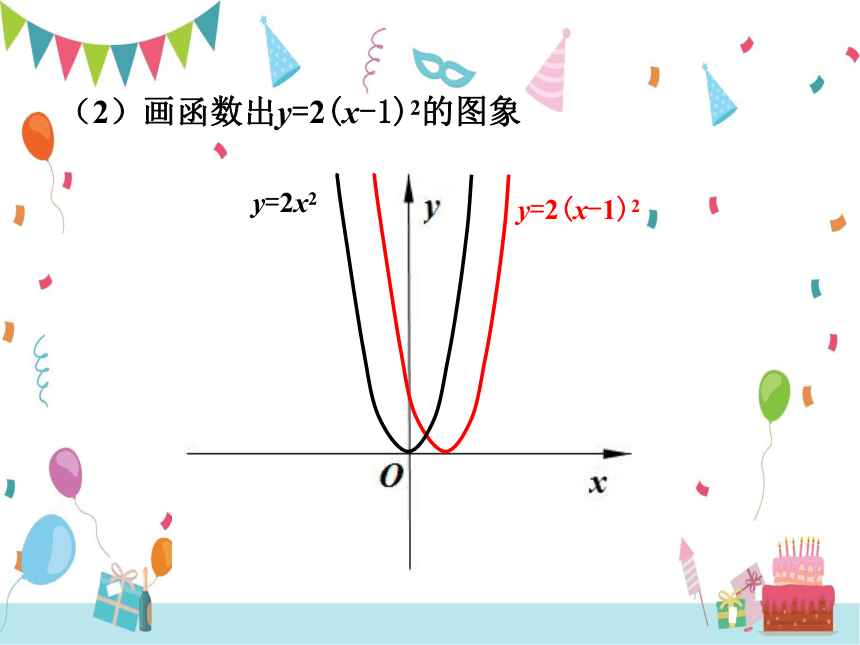
(2)画函数出y=2(x-1)2的图象
y=2x2
y=2(x-1)2
y=2(x-1)2的图象:由y=2x2的图象向右平移1个单位得到;
开口方向:向上;
对称轴:直线x=1;顶点坐标:(1, 0 );
x<1时,y随x的增大而减小,
x >1时,y随x的增大而增大.
二次函数y=2(x-1)2的图象与二次函数y=2x2的图象有什么关系?它的开口方向、对称轴、顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?
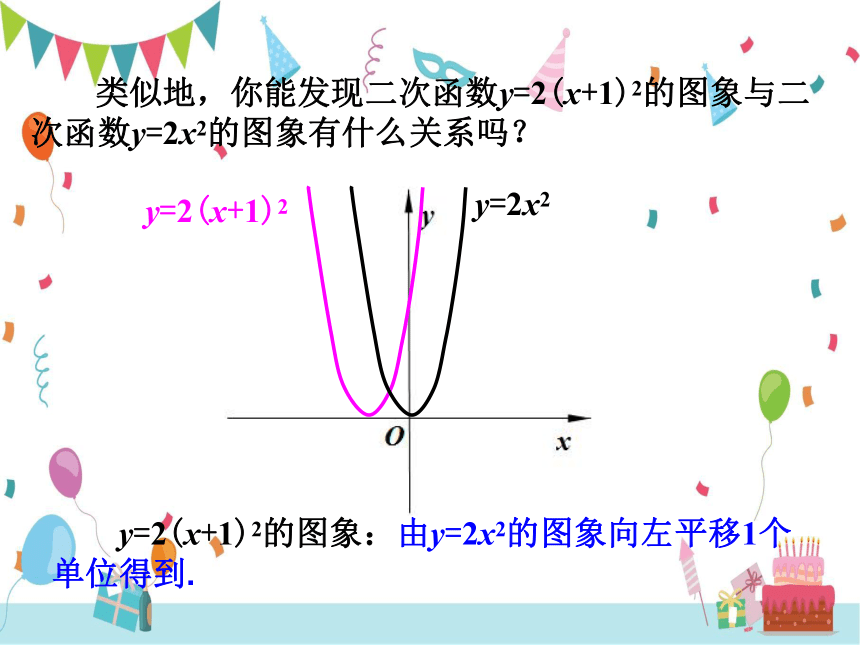
y=2(x+1)2的图象:由y=2x2的图象向左平移1个单位得到.
类似地,你能发现二次函数y=2(x+1)2的图象与二次函数y=2x2的图象有什么关系吗?
y=2(x+1)2
y=2x2
对于二次函数y=-3(x+2)2:
(1)它的图象与二次函数y=-3x2的图象有什么关系?它是轴对称图形吗?它的开口方向、对称轴、顶点坐标分别是什么?
(2)当x取哪些值时,y的随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?
随堂练习
(1)y=-3(x+2)2的图象:由y=-3x2的图象
向左平移2个单位得到;
它是轴对称图形;
开口方向:向下;
对称轴:直线x=-2;
顶点坐标:(0,-2).
(2) x<-2时,y随x的增大而增大,
x >-2时,y随x的增大而减小.
由二次函数y=2x2的图象,你能得到二次函数y=2x2- ,y=2(x+3)2,y=2(x+3)2- 的图象吗?你是怎样得到的?与同伴进行交流.
y=2x2
y=2x2-
y=2(x+3)2-
y=2(x+3)2
y=2x2- 的图象:由y=2x2的图象向下平移 个单位得到.
y=2(x+3)2的图象:由y=2x2的图象向左平移3个单位得到.
y=2(x+3)2- 的图象:由y=2x2的图象向左平移3个单位,再向下平移 个单位得到(也可由y=2x2的图象向下平移 个单位,再向左平移3个单位得到).
形状、开口大小、开口方向相同,只是位置不同.
抛物线y=a(x-h)2+k可由抛物线y=ax2沿x轴方向平移︱h︱个单位(h>0时,向右平移,h<0时,向左平移),再沿y轴方向平移︱k︱个单位(k>0时,向上平移,k<0时,向下平移)得到.
二次函数y=a(x-h)2+k与y=ax2的图象有什么关系?
归纳
二次函数y=a(x-h)2+k的图象是一条抛物线.
开口方向 对称轴 顶点坐标
y=a(x-h)2+k
向上
(a>0)
向下
(a<0)
y轴
(h,k)
归纳
增减性:
a>0时,x>h,y随x的增大而减小
x<h,y随x的增大而增大
a<0时,x>h,y随x的增大而增大
x<h,y随x的增大而减小
最值:
a>0时,x=h,y最小值=k
a<0时,x=h,y最大值=k
(1) 填空:二次函数y=-(x+3)2+2的开口方向是_____,对称轴是________,顶点坐标是_______;当x____时,y随x的增大而增大;当x_____时,y最大值=____.
(2)此抛物线怎样由抛物线y=-x2平移得到?
向下
(-3,2)
<-3
=-3
2
直线x=-3
由抛物线y=-x2先向上平移2个单位,再向左平移3个单位或先向左平移3个单位,再向上平移2个单位得到.
例题讲解
已知一个二次函数的图象的形状和抛物线y=-2x2相同,且它的顶点坐标为(1,3).
(1)求该二次函数的关系式.
(2)x取何值时,y随x的增大而增大?
(1)y=-2(x-1)2+3
(2)x<1
知识拓展
1.已知函数y=-3(x-2)2+4,当x=___时,函数取最大值为____.
2.已知抛物线y=-(x+1)2-3,当x_______时,y随x的增大而减小.
3.怎样平移抛物线y=3x2,便可得到抛物线y=3(x-2)2+2?
2
4
>-1
由抛物线y=3x2先向上平移2个单位,再向右平移3个单位或先向右平移3个单位,再向上平移2个单位得到.
随堂练习
二次函数y=a(x-h)2+k的图象是怎样的
作业:习题2.4
抛物线y=a(x-h)2+k与y=ax2有怎样的关系
二次函数y=a(x-h)2+k的性质有哪些
课堂小结
第二章
2 二次函数的图象与性质
(第3课时)
知识回顾,问题引入
1.二次函数y=ax2+c的图象是什么形状的?
2.二次函数y=ax2+c的开口方向、对称轴、顶点坐标、增减性、最值分别是怎样的?
抛物线
分a>0和a<0两种情况
x -4 -3 -2 -1 0 1 2 3 4
2x2
2(x-1)2
32
0
32
50
18
18
8
8
2
0
2
18
8
2
2
8
18
32
对于同一个y值,这两个函数对应的x值相差1(在对称轴同侧)
合作学习,探究新知
画出二次函数y=2(x-1)2的图象
(1)完成下表:
观察上表,你能发现2(x-1)2与2x2的值有什么关系?
(2)画函数出y=2(x-1)2的图象
y=2x2
y=2(x-1)2
y=2(x-1)2的图象:由y=2x2的图象向右平移1个单位得到;
开口方向:向上;
对称轴:直线x=1;顶点坐标:(1, 0 );
x<1时,y随x的增大而减小,
x >1时,y随x的增大而增大.
二次函数y=2(x-1)2的图象与二次函数y=2x2的图象有什么关系?它的开口方向、对称轴、顶点坐标分别是什么?当x取哪些值时,y的值随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?
y=2(x+1)2的图象:由y=2x2的图象向左平移1个单位得到.
类似地,你能发现二次函数y=2(x+1)2的图象与二次函数y=2x2的图象有什么关系吗?
y=2(x+1)2
y=2x2
对于二次函数y=-3(x+2)2:
(1)它的图象与二次函数y=-3x2的图象有什么关系?它是轴对称图形吗?它的开口方向、对称轴、顶点坐标分别是什么?
(2)当x取哪些值时,y的随x值的增大而增大?当x取哪些值时,y的值随x值的增大而减小?
随堂练习
(1)y=-3(x+2)2的图象:由y=-3x2的图象
向左平移2个单位得到;
它是轴对称图形;
开口方向:向下;
对称轴:直线x=-2;
顶点坐标:(0,-2).
(2) x<-2时,y随x的增大而增大,
x >-2时,y随x的增大而减小.
由二次函数y=2x2的图象,你能得到二次函数y=2x2- ,y=2(x+3)2,y=2(x+3)2- 的图象吗?你是怎样得到的?与同伴进行交流.
y=2x2
y=2x2-
y=2(x+3)2-
y=2(x+3)2
y=2x2- 的图象:由y=2x2的图象向下平移 个单位得到.
y=2(x+3)2的图象:由y=2x2的图象向左平移3个单位得到.
y=2(x+3)2- 的图象:由y=2x2的图象向左平移3个单位,再向下平移 个单位得到(也可由y=2x2的图象向下平移 个单位,再向左平移3个单位得到).
形状、开口大小、开口方向相同,只是位置不同.
抛物线y=a(x-h)2+k可由抛物线y=ax2沿x轴方向平移︱h︱个单位(h>0时,向右平移,h<0时,向左平移),再沿y轴方向平移︱k︱个单位(k>0时,向上平移,k<0时,向下平移)得到.
二次函数y=a(x-h)2+k与y=ax2的图象有什么关系?
归纳
二次函数y=a(x-h)2+k的图象是一条抛物线.
开口方向 对称轴 顶点坐标
y=a(x-h)2+k
向上
(a>0)
向下
(a<0)
y轴
(h,k)
归纳
增减性:
a>0时,x>h,y随x的增大而减小
x<h,y随x的增大而增大
a<0时,x>h,y随x的增大而增大
x<h,y随x的增大而减小
最值:
a>0时,x=h,y最小值=k
a<0时,x=h,y最大值=k
(1) 填空:二次函数y=-(x+3)2+2的开口方向是_____,对称轴是________,顶点坐标是_______;当x____时,y随x的增大而增大;当x_____时,y最大值=____.
(2)此抛物线怎样由抛物线y=-x2平移得到?
向下
(-3,2)
<-3
=-3
2
直线x=-3
由抛物线y=-x2先向上平移2个单位,再向左平移3个单位或先向左平移3个单位,再向上平移2个单位得到.
例题讲解
已知一个二次函数的图象的形状和抛物线y=-2x2相同,且它的顶点坐标为(1,3).
(1)求该二次函数的关系式.
(2)x取何值时,y随x的增大而增大?
(1)y=-2(x-1)2+3
(2)x<1
知识拓展
1.已知函数y=-3(x-2)2+4,当x=___时,函数取最大值为____.
2.已知抛物线y=-(x+1)2-3,当x_______时,y随x的增大而减小.
3.怎样平移抛物线y=3x2,便可得到抛物线y=3(x-2)2+2?
2
4
>-1
由抛物线y=3x2先向上平移2个单位,再向右平移3个单位或先向右平移3个单位,再向上平移2个单位得到.
随堂练习
二次函数y=a(x-h)2+k的图象是怎样的
作业:习题2.4
抛物线y=a(x-h)2+k与y=ax2有怎样的关系
二次函数y=a(x-h)2+k的性质有哪些
课堂小结
