北师大版六年级下学期数学立体图形特征和表面积复习课件(共19张PPT)
文档属性
| 名称 | 北师大版六年级下学期数学立体图形特征和表面积复习课件(共19张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 945.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-13 21:55:20 | ||
图片预览




文档简介
(共19张PPT)
立体图形特征和表面积复习
请同学们想一想,你能根据这些物品提出什么数学问题?
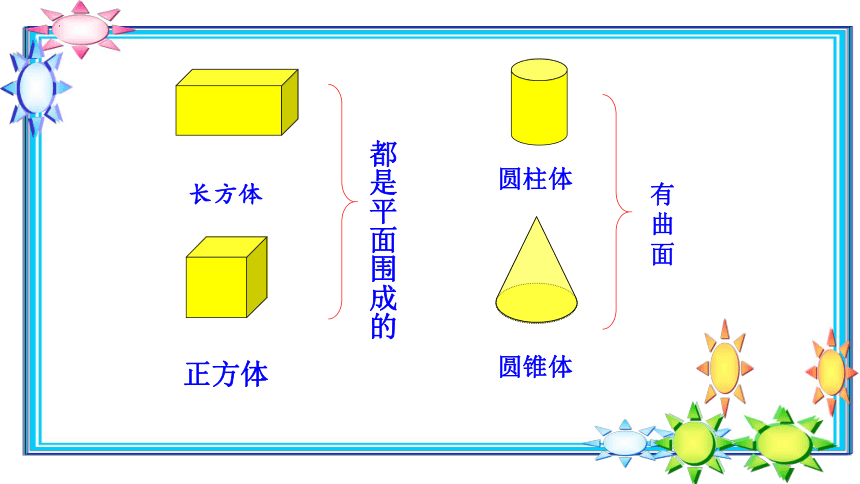
长方体
都是平面围成的
正方体
有曲面
圆柱体
圆锥体
8个
12 条
棱长
面积
面的形状
点
棱
面
12条棱的长度都相等
6个面的面积都相等
6个面都是相等的正方形
正方体
正方体是特殊的长方体
每一组互相平行的四条棱的长度相等
相对的面的面积相等
6个面一般都是长方形(也有可能有两个相对的面是正方形)
6个
长方体
关系
不同点
相同点
形体
b
h
a
a
a
a
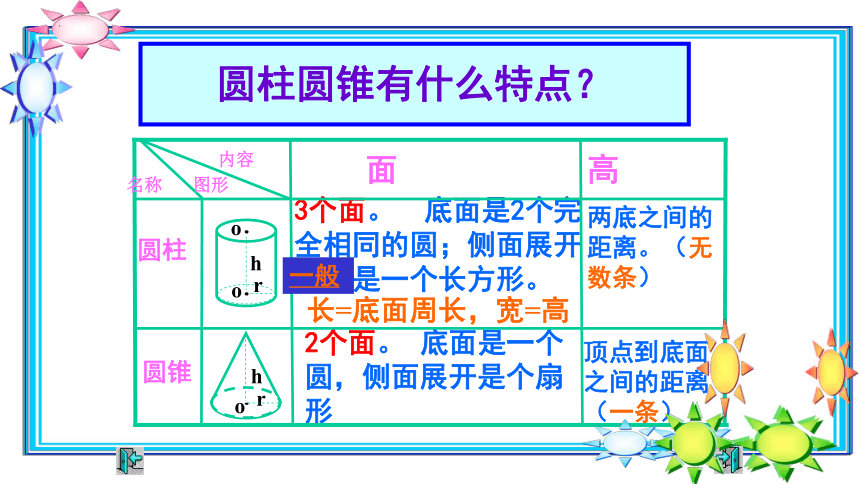
圆柱圆锥有什么特点?
顶点到底面之间的距离(一条)
2个面。 底面是一个圆,侧面展开是个扇形
圆锥
两底之间的距离。(无数条)
3个面。 底面是2个完全相同的圆;侧面展开一般是一个长方形。
圆柱
高
面
o
h
o
r
o
h
r
名称
图形
内容
长=底面周长,宽=高
一般
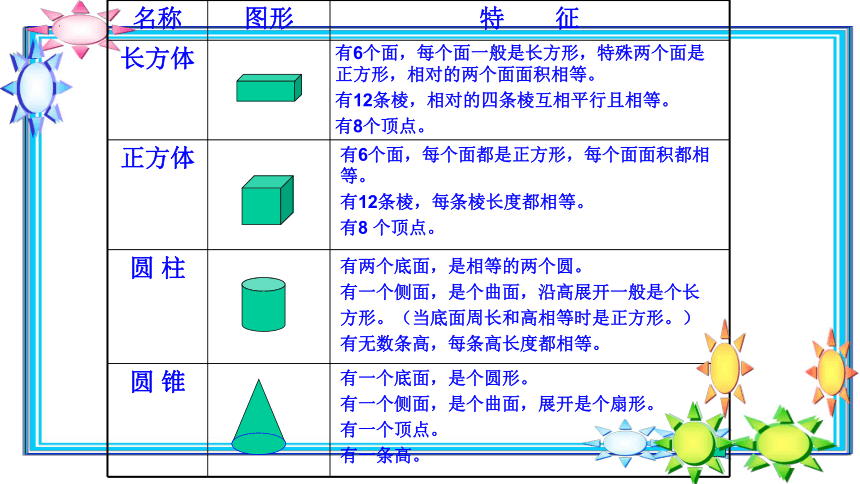
名称 图形 特 征
长方体
正方体
圆 柱
圆 锥
有6个面,每个面一般是长方形,特殊两个面是正方形,相对的两个面面积相等。
有12条棱,相对的四条棱互相平行且相等。
有8个顶点。
有6个面,每个面都是正方形,每个面面积都相等。
有12条棱,每条棱长度都相等。
有8 个顶点。
有两个底面,是相等的两个圆。
有一个侧面,是个曲面,沿高展开一般是个长
方形。(当底面周长和高相等时是正方形。)
有无数条高,每条高长度都相等。
有一个底面,是个圆形。
有一个侧面,是个曲面,展开是个扇形。
有一个顶点。
有一条高。
填空:
(1)一个长方体有 ( )条棱,相交于一点的三条棱分别叫做长方体的( )、( )、( )。
(2)一个正方体有( )个顶点,( )条棱,( )个面。
(3)正方体有( )个相等的面。
(4)圆柱体有( )条高,圆锥体有( )条高。
(5)圆柱体有( )个面,这些面中有( )个相等的面。
12
长
宽
高
8
12
6
6
无数
1
3
2
判断:
① 一个长方体最多有两个正方形。( )
② 圆柱的侧面展开不是正方形就是长方形。
( )
③ 长方体的三条棱就是它的长、宽、高。
( )
④ 圆锥的高有一条,圆柱的高有两条。
( )
√
×
×
×
解决问题:(只列式,不计算)
一个长方体的棱长总和是40厘米,其中长5厘米,宽3厘米,高是多少厘米?
40÷4-5-3
长方体的表面积= (上 面 + 前 面 + 侧 面 )×2
=(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
下面
前面
后面
左面
右面
上面
正方体的表面积=一个面的面积×6
S=6a2
上
下
前
左
后
右
底面
侧面
圆柱的表面积=侧面积+底面积×2
=底面周长×高+圆周率×半径2×2
S=ch+2 ∏ r2
底面周长
高
底面
填空:
(1)做一个长方体铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸,求商标纸的面积是求它的( )。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3) 一个圆柱形水池占地多少平方米,是求圆柱的( )。
表面积
侧面积(侧面4个面的面积)
侧面积
底面积
填空:
(4)某建筑物有几根大圆柱体要刷油漆,是求这几根圆柱体的( )。
(5)需要多少铁丝做成一个长方体框架,是求长方体的( )。
总棱长
侧面积
甲乙两人分别利用一张长20厘米,宽15厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱( )。
A高一定相等
B侧面积一定相等
C侧面积和高都相等
D侧面积和高都不相等
B
抢答题
8
4
6
6
6
6
6
6
比一比:哪个纸盒所用的硬纸板面积大?(单位:cm)
思考题:把一个长、宽、高分别是5厘米、4厘米、3厘米的长方体截成两个长方体后,表面积最多增加多少?
2、有一个圆柱的底面积是12.56平方厘米,侧面展开是一个正方形,这个圆柱体的侧面积是多少平方厘米?
1、一个长方体木箱,长是60cm,宽是50cm ,高是40cm,这个木箱的占地面积是多少?表面积是多少?
挑战自我:
温故而知新
学无定法,贵在得法
万变不离其宗
立体图形特征和表面积复习
请同学们想一想,你能根据这些物品提出什么数学问题?
长方体
都是平面围成的
正方体
有曲面
圆柱体
圆锥体
8个
12 条
棱长
面积
面的形状
点
棱
面
12条棱的长度都相等
6个面的面积都相等
6个面都是相等的正方形
正方体
正方体是特殊的长方体
每一组互相平行的四条棱的长度相等
相对的面的面积相等
6个面一般都是长方形(也有可能有两个相对的面是正方形)
6个
长方体
关系
不同点
相同点
形体
b
h
a
a
a
a
圆柱圆锥有什么特点?
顶点到底面之间的距离(一条)
2个面。 底面是一个圆,侧面展开是个扇形
圆锥
两底之间的距离。(无数条)
3个面。 底面是2个完全相同的圆;侧面展开一般是一个长方形。
圆柱
高
面
o
h
o
r
o
h
r
名称
图形
内容
长=底面周长,宽=高
一般
名称 图形 特 征
长方体
正方体
圆 柱
圆 锥
有6个面,每个面一般是长方形,特殊两个面是正方形,相对的两个面面积相等。
有12条棱,相对的四条棱互相平行且相等。
有8个顶点。
有6个面,每个面都是正方形,每个面面积都相等。
有12条棱,每条棱长度都相等。
有8 个顶点。
有两个底面,是相等的两个圆。
有一个侧面,是个曲面,沿高展开一般是个长
方形。(当底面周长和高相等时是正方形。)
有无数条高,每条高长度都相等。
有一个底面,是个圆形。
有一个侧面,是个曲面,展开是个扇形。
有一个顶点。
有一条高。
填空:
(1)一个长方体有 ( )条棱,相交于一点的三条棱分别叫做长方体的( )、( )、( )。
(2)一个正方体有( )个顶点,( )条棱,( )个面。
(3)正方体有( )个相等的面。
(4)圆柱体有( )条高,圆锥体有( )条高。
(5)圆柱体有( )个面,这些面中有( )个相等的面。
12
长
宽
高
8
12
6
6
无数
1
3
2
判断:
① 一个长方体最多有两个正方形。( )
② 圆柱的侧面展开不是正方形就是长方形。
( )
③ 长方体的三条棱就是它的长、宽、高。
( )
④ 圆锥的高有一条,圆柱的高有两条。
( )
√
×
×
×
解决问题:(只列式,不计算)
一个长方体的棱长总和是40厘米,其中长5厘米,宽3厘米,高是多少厘米?
40÷4-5-3
长方体的表面积= (上 面 + 前 面 + 侧 面 )×2
=(长×宽+长×高+宽×高)×2
S=(ab+ah+bh)×2
下面
前面
后面
左面
右面
上面
正方体的表面积=一个面的面积×6
S=6a2
上
下
前
左
后
右
底面
侧面
圆柱的表面积=侧面积+底面积×2
=底面周长×高+圆周率×半径2×2
S=ch+2 ∏ r2
底面周长
高
底面
填空:
(1)做一个长方体铁皮罐头盒,求需要多少铁皮,是求它的( ),罐头盒周围贴商标纸,求商标纸的面积是求它的( )。
(2)做一只圆柱形通风管要用多少铁皮,是求它的( )。
(3) 一个圆柱形水池占地多少平方米,是求圆柱的( )。
表面积
侧面积(侧面4个面的面积)
侧面积
底面积
填空:
(4)某建筑物有几根大圆柱体要刷油漆,是求这几根圆柱体的( )。
(5)需要多少铁丝做成一个长方体框架,是求长方体的( )。
总棱长
侧面积
甲乙两人分别利用一张长20厘米,宽15厘米的纸用两种不同的方法围成一个圆柱体(接头处不重叠),那么围成的圆柱( )。
A高一定相等
B侧面积一定相等
C侧面积和高都相等
D侧面积和高都不相等
B
抢答题
8
4
6
6
6
6
6
6
比一比:哪个纸盒所用的硬纸板面积大?(单位:cm)
思考题:把一个长、宽、高分别是5厘米、4厘米、3厘米的长方体截成两个长方体后,表面积最多增加多少?
2、有一个圆柱的底面积是12.56平方厘米,侧面展开是一个正方形,这个圆柱体的侧面积是多少平方厘米?
1、一个长方体木箱,长是60cm,宽是50cm ,高是40cm,这个木箱的占地面积是多少?表面积是多少?
挑战自我:
温故而知新
学无定法,贵在得法
万变不离其宗
