2021-2022学年人教版数学八年级下册 19.1.1 变量与函数 课件(共26张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册 19.1.1 变量与函数 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 00:00:00 | ||
图片预览






文档简介
(共26张PPT)
八年级 下册
19.1 变量与函数(1)
第十九章 一次函数
19.1 函数
变量与函数的概念;
函数的三种表示方法——解析法、列表法、图像法
19.2 一次函数
正比例函数的图像和性质;一次函数的图像和性质
本章将从初步认识变量和函数开始,重点学习
一类最基本的一次函数,结合它的图像讨论它的性
质,并利用它研究一些数学问题和实际问题。感受
函数在解决运动变化问题中的重要作用。
课件说明
学习目标:
1.了解变量与常量的意义;
2.了解函数的概念.
学习重点:
了解变量与常量的意义,充分体会运动变化过程中
量的变化.
本课是函数的起始课,函数是刻画运动变化现象的
重要数学模型,要从数学的角度研究变化现象,把
握变化规律,首先要关注变化过程中量的变化,这
就是变量,本课在充分体会运动变化过程中数量变
化的基础上,领会变量与常量的含义.
课件说明
变量与函数
(1)汽车以60 千米/时的速度匀速行驶,行驶时间
为t 小时,行驶路程为 s千米 .
数值不断变化的量
变量
数值固定不变的量
常量
运动变化问题
变量与函数
(2)每张电影票的售价为10 元,设某场电影售出x
张票,票房收入为y 元.
售出x张票,票房收入为y 元是变量
售价为10 元是常量
变量与函数
(3)圆形水波慢慢地扩大,在这一过程中,圆的
半径r 厘米 ,圆的面积为S 平方厘米,圆周率(圆周长
与直径之比)为π.
圆的半径r 厘米 ,圆的面积为S 平方厘米是变量
圆周率π是常量
变量与函数
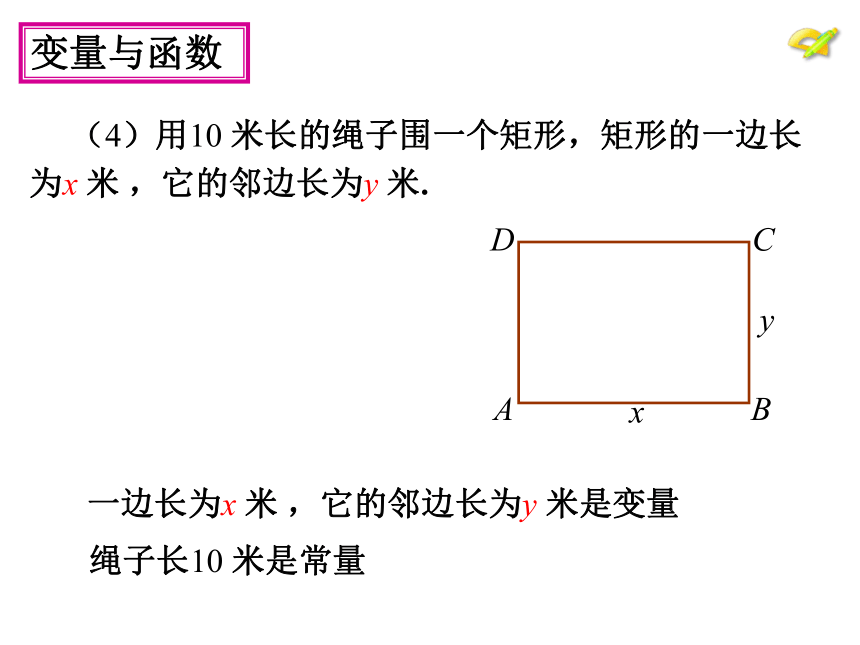
(4)用10 米长的绳子围一个矩形,矩形的一边长
为x 米 ,它的邻边长为y 米.
x
y
A
B
C
D
一边长为x 米 ,它的邻边长为y 米是变量
绳子长10 米是常量
辨一辨
指出下列变化过程中的变量和常量:
(1)某市的自来水价为4元/吨,现要抽取若干户居民调查水费支出情况,记某户月用水量为 x 吨,月应交水费为 y 元;
(2)某地手机通话费为0.2元/分,李明在手机话费卡中存入30元,记此后他的手机通话时间为t 分,话费卡中的余额为w 元;
(3)水中涟漪(圆形水波)不断扩大,记它的半径为r,圆周长为C,圆周率(圆周长与直径之比)为π;
(4)把10本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本。
行驶时间 t/h 1 3 3.4 4 9 …
行驶路程s/km …
60
180
204
240
540
观察思考 分析变化
问题 下面变化过程中的变量之间有什么联系?
(1)汽车以60 千米/时 的速度匀速行驶,行驶时间
为t 小时,行驶路程为 s千米 .
对于 t 的每一个确定的值,s 都有唯一确定的值与其对应
单值对应的关系
观察思考 分析变化
问题1 下面变化过程中的变量之间有什么联系?
(2)每张电影票的售价为10 元,设某场电影售出x
张票,票房收入为y 元.
售出票数 x /张 100 120 140 160 180 …
票房收入y/元 …
1000
1200
1400
1600
1800
对于 x的每一个确定的值,y 都有唯一确定的值与其对应
单值对应的关系
圆的半径 r/cm 10 20 30 40 50 …
圆的面积S/cm2 …
100π
400π
900π
1600π
2500π
观察思考 分析变化
问题1 下面变化过程中的变量之间有什么联系?
(3)圆形水波慢慢地扩大,在这一过程中,圆的
半径r 厘米 ,圆的面积为S 平方厘米.
对于 r的每一个确定的值,S 都有唯一确定的值与其对应
单值对应的关系
观察思考 分析变化
问题1 下面变化过程中的变量之间有什么联系?
矩形长 x /米 3 3.5 4 4.5 …
矩形宽 y/米 …
2
1.5
1
0.5
(4)用10 米长的绳子围一个矩形,矩形的一边长
为x 米 ,它的邻边长为y 米.
对于 x的每一个确定的值,y 都有唯一确定的值与其对应
单值对应的关系
行驶时间 t/h 1 3 3.4 4 9 …
行驶路程s/km …
60
180
204
240
540
观察思考 分析变化
(1)汽车以60 千米/时 的速度匀速行驶,行驶时间
为t 小时,行驶路程为 s千米 .
对于 t 的每一个确定的值,s 都有唯一确定的值与其对应
单值对应的关系
t是自变量
s是t的函数
观察思考 分析变化
(2)每张电影票的售价为10 元,设某场电影售出x
张票,票房收入为y 元.
售出票数 x /张 100 120 140 160 180 …
票房收入y/元 …
1000
1200
1400
1600
1800
对于 x的每一个确定的值,y 都有唯一确定的值与其对应
单值对应的关系
x是自变量
y是x的函数
圆的半径 r/cm 10 20 30 40 50 …
圆的面积S/cm2 …
100π
400π
900π
1600π
2500π
观察思考 分析变化
(3)圆形水波慢慢地扩大,在这一过程中,圆的
半径r 厘米 ,圆的面积为S 平方厘米.
对于 r的每一个确定的值,S 都有唯一确定的值与其对应
单值对应的关系
r是自变量
S是r的函数
观察思考 分析变化
矩形长 x /米 3 3.5 4 4.5 …
矩形宽 y/米 …
2
1.5
1
0.5
(4)用10 米长的绳子围一个矩形,矩形的一边长
为x 米 ,它的邻边长为y 米.
对于 x的每一个确定的值,y 都有唯一确定的值与其对应
单值对应的关系
x是自变量
y是x的函数
观察思考 再次概括
函数的定义:
一般地,在一个变化过程中,如果有两个变量 x 与
y,并且对于 x 的每一个确定的值,y 都有唯一确定的值
与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
函数的产生:运动变化的问题
函数的前提:有两个变量,并且是单值对应的关系
函数的作用:描述两个变量的单值对应关系
描述方法:一个变量是自变量,另一个变量是它的函数
观察思考 分析变化
矩形长 x /米 3 3.5 4 4.5 …
矩形宽 y/米 …
2
1.5
1
0.5
(4)用10 米长的绳子围一个矩形,矩形的一边长
为x 米 ,它的邻边长为y 米.
主动变化的量为自变量,随之变化的量为函数。
y是自变量
x是y的函数
初步应用 巩固知识
练习2 函数的判断
(1)改变正方形的边长 x,正方形的面积 S 随之变化;
正方形的面积S 是边长 x的函数吗?为什么?
正方形的面积S 是边长 x的函数。
因为这是一个运动变化的问题,有两个变量,并且是
单值对应的关系。
初步应用 巩固知识
练习2 函数的判断
(2)向一水池每分钟注水0.1 m3,注水量 y(单位:
m3)是注水时间 x(单位:min)的函数吗?为什么?
注水量 y是注水时间 x的函数。
因为这是一个运动变化的问题,有两个变量,并且是
单值对应的关系。
初步应用 巩固知识
练习2 函数的判断
(3)秀水村的耕地面积是106 m2,这个村人均占有耕
地面积 y (单位:m2)是这个村人数 n 的函数吗?
为什么?
这个村人均占有耕地面积 y 是这个村人数 n的函数。
因为这是一个运动变化的问题,有两个变量,并且是
单值对应的关系。
初步应用 巩固知识
练习2 函数的判断
(4)P是数轴上的一个动点,它到原点的距离记为 x,
它的坐标记为 y,y 是 x 的函数吗?为什么?
y 不是 x 的函数。
因为这是一个运动变化的问题,有两个变量,但不是
单值对应的关系。
比如当距离x=1时,坐标y=±1
课堂小结
1、在运动变化的问题中,数值不断变化的量叫
______,数值固定不变的量叫_______.
变量
常量
2、函数的定义:
一般地,在一个变化过程中,如果有两个变量 x 与
y,并且对于 x 的每一个确定的值,y 都有________
的值与其对应,那么我们就说 x 是______,y 是 x
______.
唯一确定
自变量
函数
作业:课堂10分钟.
课后作业
八年级 下册
19.1 变量与函数(1)
第十九章 一次函数
19.1 函数
变量与函数的概念;
函数的三种表示方法——解析法、列表法、图像法
19.2 一次函数
正比例函数的图像和性质;一次函数的图像和性质
本章将从初步认识变量和函数开始,重点学习
一类最基本的一次函数,结合它的图像讨论它的性
质,并利用它研究一些数学问题和实际问题。感受
函数在解决运动变化问题中的重要作用。
课件说明
学习目标:
1.了解变量与常量的意义;
2.了解函数的概念.
学习重点:
了解变量与常量的意义,充分体会运动变化过程中
量的变化.
本课是函数的起始课,函数是刻画运动变化现象的
重要数学模型,要从数学的角度研究变化现象,把
握变化规律,首先要关注变化过程中量的变化,这
就是变量,本课在充分体会运动变化过程中数量变
化的基础上,领会变量与常量的含义.
课件说明
变量与函数
(1)汽车以60 千米/时的速度匀速行驶,行驶时间
为t 小时,行驶路程为 s千米 .
数值不断变化的量
变量
数值固定不变的量
常量
运动变化问题
变量与函数
(2)每张电影票的售价为10 元,设某场电影售出x
张票,票房收入为y 元.
售出x张票,票房收入为y 元是变量
售价为10 元是常量
变量与函数
(3)圆形水波慢慢地扩大,在这一过程中,圆的
半径r 厘米 ,圆的面积为S 平方厘米,圆周率(圆周长
与直径之比)为π.
圆的半径r 厘米 ,圆的面积为S 平方厘米是变量
圆周率π是常量
变量与函数
(4)用10 米长的绳子围一个矩形,矩形的一边长
为x 米 ,它的邻边长为y 米.
x
y
A
B
C
D
一边长为x 米 ,它的邻边长为y 米是变量
绳子长10 米是常量
辨一辨
指出下列变化过程中的变量和常量:
(1)某市的自来水价为4元/吨,现要抽取若干户居民调查水费支出情况,记某户月用水量为 x 吨,月应交水费为 y 元;
(2)某地手机通话费为0.2元/分,李明在手机话费卡中存入30元,记此后他的手机通话时间为t 分,话费卡中的余额为w 元;
(3)水中涟漪(圆形水波)不断扩大,记它的半径为r,圆周长为C,圆周率(圆周长与直径之比)为π;
(4)把10本书随意放入两个抽屉(每个抽屉内都放),第一个抽屉放入x本,第二个抽屉放入y本。
行驶时间 t/h 1 3 3.4 4 9 …
行驶路程s/km …
60
180
204
240
540
观察思考 分析变化
问题 下面变化过程中的变量之间有什么联系?
(1)汽车以60 千米/时 的速度匀速行驶,行驶时间
为t 小时,行驶路程为 s千米 .
对于 t 的每一个确定的值,s 都有唯一确定的值与其对应
单值对应的关系
观察思考 分析变化
问题1 下面变化过程中的变量之间有什么联系?
(2)每张电影票的售价为10 元,设某场电影售出x
张票,票房收入为y 元.
售出票数 x /张 100 120 140 160 180 …
票房收入y/元 …
1000
1200
1400
1600
1800
对于 x的每一个确定的值,y 都有唯一确定的值与其对应
单值对应的关系
圆的半径 r/cm 10 20 30 40 50 …
圆的面积S/cm2 …
100π
400π
900π
1600π
2500π
观察思考 分析变化
问题1 下面变化过程中的变量之间有什么联系?
(3)圆形水波慢慢地扩大,在这一过程中,圆的
半径r 厘米 ,圆的面积为S 平方厘米.
对于 r的每一个确定的值,S 都有唯一确定的值与其对应
单值对应的关系
观察思考 分析变化
问题1 下面变化过程中的变量之间有什么联系?
矩形长 x /米 3 3.5 4 4.5 …
矩形宽 y/米 …
2
1.5
1
0.5
(4)用10 米长的绳子围一个矩形,矩形的一边长
为x 米 ,它的邻边长为y 米.
对于 x的每一个确定的值,y 都有唯一确定的值与其对应
单值对应的关系
行驶时间 t/h 1 3 3.4 4 9 …
行驶路程s/km …
60
180
204
240
540
观察思考 分析变化
(1)汽车以60 千米/时 的速度匀速行驶,行驶时间
为t 小时,行驶路程为 s千米 .
对于 t 的每一个确定的值,s 都有唯一确定的值与其对应
单值对应的关系
t是自变量
s是t的函数
观察思考 分析变化
(2)每张电影票的售价为10 元,设某场电影售出x
张票,票房收入为y 元.
售出票数 x /张 100 120 140 160 180 …
票房收入y/元 …
1000
1200
1400
1600
1800
对于 x的每一个确定的值,y 都有唯一确定的值与其对应
单值对应的关系
x是自变量
y是x的函数
圆的半径 r/cm 10 20 30 40 50 …
圆的面积S/cm2 …
100π
400π
900π
1600π
2500π
观察思考 分析变化
(3)圆形水波慢慢地扩大,在这一过程中,圆的
半径r 厘米 ,圆的面积为S 平方厘米.
对于 r的每一个确定的值,S 都有唯一确定的值与其对应
单值对应的关系
r是自变量
S是r的函数
观察思考 分析变化
矩形长 x /米 3 3.5 4 4.5 …
矩形宽 y/米 …
2
1.5
1
0.5
(4)用10 米长的绳子围一个矩形,矩形的一边长
为x 米 ,它的邻边长为y 米.
对于 x的每一个确定的值,y 都有唯一确定的值与其对应
单值对应的关系
x是自变量
y是x的函数
观察思考 再次概括
函数的定义:
一般地,在一个变化过程中,如果有两个变量 x 与
y,并且对于 x 的每一个确定的值,y 都有唯一确定的值
与其对应,那么我们就说 x 是自变量,y 是 x 的函数.
函数的产生:运动变化的问题
函数的前提:有两个变量,并且是单值对应的关系
函数的作用:描述两个变量的单值对应关系
描述方法:一个变量是自变量,另一个变量是它的函数
观察思考 分析变化
矩形长 x /米 3 3.5 4 4.5 …
矩形宽 y/米 …
2
1.5
1
0.5
(4)用10 米长的绳子围一个矩形,矩形的一边长
为x 米 ,它的邻边长为y 米.
主动变化的量为自变量,随之变化的量为函数。
y是自变量
x是y的函数
初步应用 巩固知识
练习2 函数的判断
(1)改变正方形的边长 x,正方形的面积 S 随之变化;
正方形的面积S 是边长 x的函数吗?为什么?
正方形的面积S 是边长 x的函数。
因为这是一个运动变化的问题,有两个变量,并且是
单值对应的关系。
初步应用 巩固知识
练习2 函数的判断
(2)向一水池每分钟注水0.1 m3,注水量 y(单位:
m3)是注水时间 x(单位:min)的函数吗?为什么?
注水量 y是注水时间 x的函数。
因为这是一个运动变化的问题,有两个变量,并且是
单值对应的关系。
初步应用 巩固知识
练习2 函数的判断
(3)秀水村的耕地面积是106 m2,这个村人均占有耕
地面积 y (单位:m2)是这个村人数 n 的函数吗?
为什么?
这个村人均占有耕地面积 y 是这个村人数 n的函数。
因为这是一个运动变化的问题,有两个变量,并且是
单值对应的关系。
初步应用 巩固知识
练习2 函数的判断
(4)P是数轴上的一个动点,它到原点的距离记为 x,
它的坐标记为 y,y 是 x 的函数吗?为什么?
y 不是 x 的函数。
因为这是一个运动变化的问题,有两个变量,但不是
单值对应的关系。
比如当距离x=1时,坐标y=±1
课堂小结
1、在运动变化的问题中,数值不断变化的量叫
______,数值固定不变的量叫_______.
变量
常量
2、函数的定义:
一般地,在一个变化过程中,如果有两个变量 x 与
y,并且对于 x 的每一个确定的值,y 都有________
的值与其对应,那么我们就说 x 是______,y 是 x
______.
唯一确定
自变量
函数
作业:课堂10分钟.
课后作业
