2021-2022学年人教版数学八年级下册 19.2.2一次函数 待定系数法求一次函数的解析式 课件(共20张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学八年级下册 19.2.2一次函数 待定系数法求一次函数的解析式 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 210.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 09:26:01 | ||
图片预览





文档简介
(共20张PPT)
确定一次函数表达式
1、一次函数与正比例函数之间有什么
联系?
一次函数
正比例
函数
温故而知新
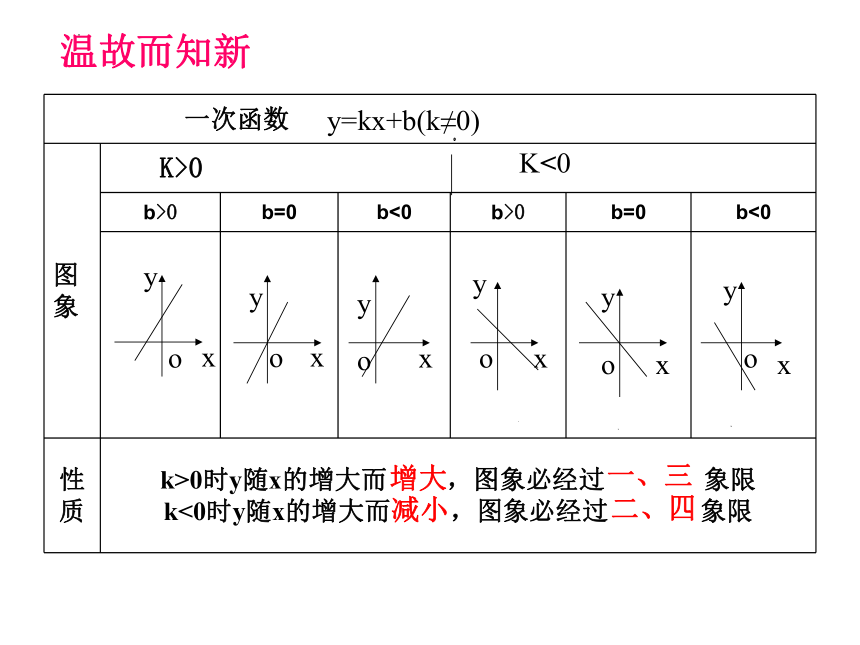
一次函数
图象 K>0
b>0 b=0 b<0 b>0 b=0 b<0
性质 k>0时y随x的增大而 ,图象必经过 象限 k<0时y随x的增大而 ,图象必经过 象限
x
x
y
y
x
y
o
o
o
x
y
o
x
y
o
x
y
o
减小
增大
一、三
二、四
温故而知新
y=kx+b(k≠0)
K<0
你清楚了吗?
一次函数 y=kx+b(k≠0) 的图象是一条直线,一次项系数 确定直线的增减性,常数项 决定直线与 轴交点的位置.
2、设y1=k1x+b1,y2=k2x+b2 为两条直线
当k1=k2,b1=b2时
k1=k2,b1≠b2时
k1≠k2,b1=b2时
重合
平行
相交且与y轴交于同一点
温故而知新
V/(米/秒)
t/秒
O
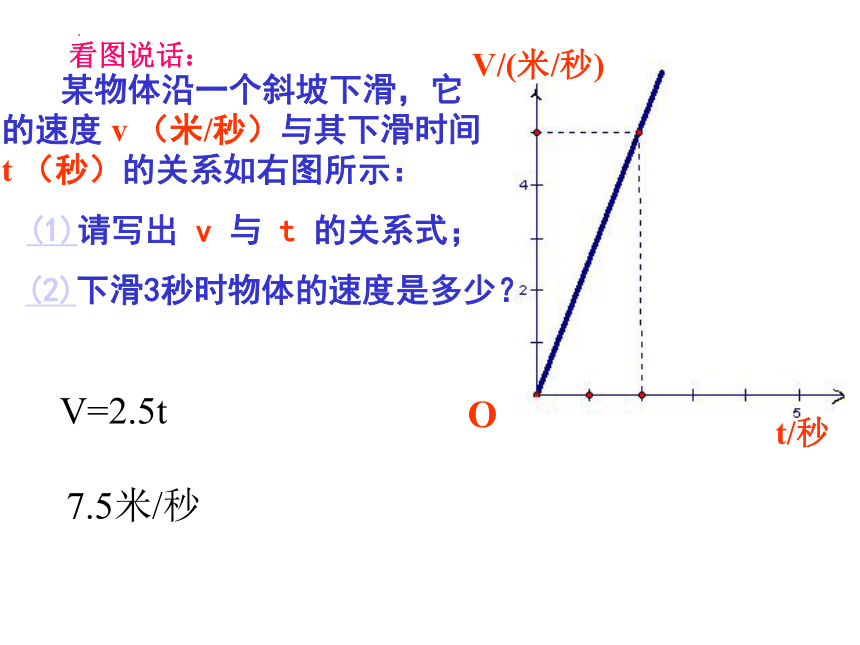
某物体沿一个斜坡下滑,它的速度 v (米/秒)与其下滑时间 t (秒)的关系如右图所示:
(1)请写出 v 与 t 的关系式;
(2)下滑3秒时物体的速度是多少?
V=2.5t
7.5米/秒
看图说话:
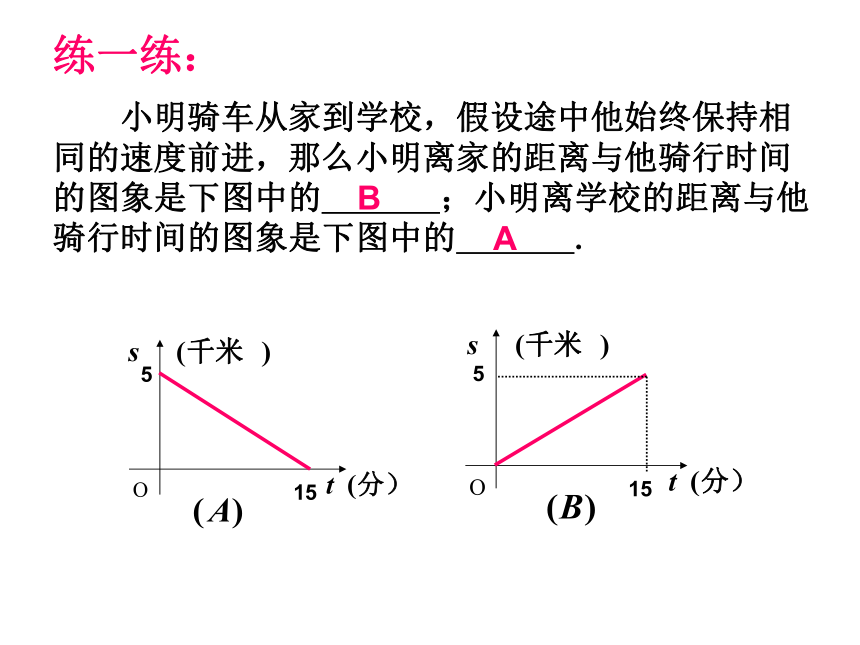
小明骑车从家到学校,假设途中他始终保持相同的速度前进,那么小明离家的距离与他骑行时间的图象是下图中的 ;小明离学校的距离与他骑行时间的图象是下图中的 .
15
5
15
5
B
A
练一练:
动脑筋
请同学从这些题的解题过程中,总结一下
如果已知函数图象,我们应该怎么样求函数
的表达式?
想一想
确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
只需一个
需要两个条件
先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法, --待定系数法
求函数解析式的方法:
确定一次函数表达式
①通过观察图象或由条件确定其是正比例函数还是一次函数,然后设其表达式为
y=kx+b(k≠0),或者y=kx(k≠0)
②把已知点的坐标代入,若是正比例函数则需要一个点,若是一次函数,则需要二个点,组成关于k、b的一个或两个方程。
③解方程(组)得k、b的值。
④把k、b代回到表达式中,得到明朗化的解析式。
例1 在弹性限度内,弹簧的长度 y(厘米)是所挂物体质量 x(千克)的一次函数。一根弹簧不挂物体时长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米。请写出 y 与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度。
解:
设 y=kx+b ,根据题意,得 14.5=b , (1) 16=3k+b, (2) 将 b=14.5 代入(2),得k=0.5 。 所以在弹性限度内,y=0.5x+14.5 。 当 x=4 时,y=0.5 x 4+14.5=16.5 (厘米)。 即物体的质量为4千克时,弹簧的长度为16.5厘米。
例2:一次函数的图象过M(3,2),N(-1, - 6)
(1)求函数的解析式;
(2)试判断点P(2a,4a-4)是否在函数的图象上,并说明理由;
练习(1)
若函数y=kx+b的图像经过点(-3,-2)和(1,6)
求k、b及函数关系式。
练习(2)
一次函数的图象经过点(0,2)和点(4,6)。
(1)写出一次函数的表达式。
(2)求出这个一次函数与两坐标轴所围成三角形的面积。
例3: 已知一次函数的图象如下图,写出它的关系式.
0
B
A
x
y
分析 :从“形” 看,图象经过x轴上横坐标为2的点,y轴上纵坐标是-3的点.从“数”看,坐标(2,0),(0,-3)满足解析式.
-3
2
已知一次函数y=kx+b(k ≠0)与x轴交于点A(m,0)与y轴交于点B(0,n)则解析式为y=- x+n
练习:
已知函数y=kx+1与y=-0.5x+b的图象
相交于点(2,5),则k,b为( )
A、K=2 ,b=6 B、k=-2 ,b=7
C、K=1 ,B=5 D、k=2 ,b=-6
A
已知一次函数y=kx+b的图像与y轴交于点B且OB长为2,与X轴交于点A且S AOB =2求直线AB的解析式 。
数学乐园
讨论
小结
你在本节课当中收获了哪些知识?与同伴交流一下。
确定一次函数表达式
①通过观察图象或由条件确定其是正比例函数还是一次函数,然后设其表达式为
y=kx+b(k≠0),或者y=kx(k≠0)
②把已知点的坐标代入,若是正比例函数则需要一个点,若是一次函数,则需要二个点,组成关于k、b的一个或两个方程。
③解方程(组)得k、b的值。
④把k、b代回到表达式中,得到明朗化的解析式。
课时作业本19.2.2
作业
确定一次函数表达式
1、一次函数与正比例函数之间有什么
联系?
一次函数
正比例
函数
温故而知新
一次函数
图象 K>0
b>0 b=0 b<0 b>0 b=0 b<0
性质 k>0时y随x的增大而 ,图象必经过 象限 k<0时y随x的增大而 ,图象必经过 象限
x
x
y
y
x
y
o
o
o
x
y
o
x
y
o
x
y
o
减小
增大
一、三
二、四
温故而知新
y=kx+b(k≠0)
K<0
你清楚了吗?
一次函数 y=kx+b(k≠0) 的图象是一条直线,一次项系数 确定直线的增减性,常数项 决定直线与 轴交点的位置.
2、设y1=k1x+b1,y2=k2x+b2 为两条直线
当k1=k2,b1=b2时
k1=k2,b1≠b2时
k1≠k2,b1=b2时
重合
平行
相交且与y轴交于同一点
温故而知新
V/(米/秒)
t/秒
O
某物体沿一个斜坡下滑,它的速度 v (米/秒)与其下滑时间 t (秒)的关系如右图所示:
(1)请写出 v 与 t 的关系式;
(2)下滑3秒时物体的速度是多少?
V=2.5t
7.5米/秒
看图说话:
小明骑车从家到学校,假设途中他始终保持相同的速度前进,那么小明离家的距离与他骑行时间的图象是下图中的 ;小明离学校的距离与他骑行时间的图象是下图中的 .
15
5
15
5
B
A
练一练:
动脑筋
请同学从这些题的解题过程中,总结一下
如果已知函数图象,我们应该怎么样求函数
的表达式?
想一想
确定正比例函数的表达式需要几个条件?
确定一次函数的表达式呢?
只需一个
需要两个条件
先设出函数解析式,再根据条件确定解析式中未知的系数,从而具体写出这个式子的方法, --待定系数法
求函数解析式的方法:
确定一次函数表达式
①通过观察图象或由条件确定其是正比例函数还是一次函数,然后设其表达式为
y=kx+b(k≠0),或者y=kx(k≠0)
②把已知点的坐标代入,若是正比例函数则需要一个点,若是一次函数,则需要二个点,组成关于k、b的一个或两个方程。
③解方程(组)得k、b的值。
④把k、b代回到表达式中,得到明朗化的解析式。
例1 在弹性限度内,弹簧的长度 y(厘米)是所挂物体质量 x(千克)的一次函数。一根弹簧不挂物体时长14.5厘米;当所挂物体的质量为3千克时,弹簧长16厘米。请写出 y 与x之间的关系式,并求当所挂物体的质量为4千克时弹簧的长度。
解:
设 y=kx+b ,根据题意,得 14.5=b , (1) 16=3k+b, (2) 将 b=14.5 代入(2),得k=0.5 。 所以在弹性限度内,y=0.5x+14.5 。 当 x=4 时,y=0.5 x 4+14.5=16.5 (厘米)。 即物体的质量为4千克时,弹簧的长度为16.5厘米。
例2:一次函数的图象过M(3,2),N(-1, - 6)
(1)求函数的解析式;
(2)试判断点P(2a,4a-4)是否在函数的图象上,并说明理由;
练习(1)
若函数y=kx+b的图像经过点(-3,-2)和(1,6)
求k、b及函数关系式。
练习(2)
一次函数的图象经过点(0,2)和点(4,6)。
(1)写出一次函数的表达式。
(2)求出这个一次函数与两坐标轴所围成三角形的面积。
例3: 已知一次函数的图象如下图,写出它的关系式.
0
B
A
x
y
分析 :从“形” 看,图象经过x轴上横坐标为2的点,y轴上纵坐标是-3的点.从“数”看,坐标(2,0),(0,-3)满足解析式.
-3
2
已知一次函数y=kx+b(k ≠0)与x轴交于点A(m,0)与y轴交于点B(0,n)则解析式为y=- x+n
练习:
已知函数y=kx+1与y=-0.5x+b的图象
相交于点(2,5),则k,b为( )
A、K=2 ,b=6 B、k=-2 ,b=7
C、K=1 ,B=5 D、k=2 ,b=-6
A
已知一次函数y=kx+b的图像与y轴交于点B且OB长为2,与X轴交于点A且S AOB =2求直线AB的解析式 。
数学乐园
讨论
小结
你在本节课当中收获了哪些知识?与同伴交流一下。
确定一次函数表达式
①通过观察图象或由条件确定其是正比例函数还是一次函数,然后设其表达式为
y=kx+b(k≠0),或者y=kx(k≠0)
②把已知点的坐标代入,若是正比例函数则需要一个点,若是一次函数,则需要二个点,组成关于k、b的一个或两个方程。
③解方程(组)得k、b的值。
④把k、b代回到表达式中,得到明朗化的解析式。
课时作业本19.2.2
作业
