11.2三角形全等的判定课时作业(附答案)
文档属性
| 名称 | 11.2三角形全等的判定课时作业(附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 116.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-04 00:00:00 | ||
图片预览




文档简介
11.2三角形全等的判定课时作业(附答案)
姓名:_______________班级:_______________考号:_______________
一、选择题
1、如图,△ABC与△BDE都是等边三角形,ABA.AE=CD????? B.AE>CD????? C.AE2、如右图, 小强利用全等三角形的知识测量池塘两端M、N的距离,如果△PQO≌△NMO,则只需测出其长度的线段是(???? )
A.PO B.PQ??????? C.MO D.MQ
3、如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF ∥BC, 平移△AEF可以得到的三角形是(????? )
A.△BDF???? B.△DEF???? C.△CDE???? D.△BDF和△CDE
4、如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD??? B.∠BAC=∠DAC? C.∠BCA=∠DCA? D.∠B=∠D=90°
5、如图,△ABC≌△DCB,若∠A=80°,∠ACB=40°,则∠BCD等于( ???)
A.80°? B.60°? C.40°? D.20°
6、下列两个三角形中,一定全等的是( ???)
A. 两个等边三角形
B. 有一个角是40°,腰相等的两个等腰三角形
C. 有一条边相等,有一个内角相等的两个等腰三角形
D. 有一个角是100°,底相等的两个等腰三角形
7、下列说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;
④有一条边相等的两个等腰直角三角形全等.其中正确的有(?? ).
A、1个 B、2个 C、3个 D、4个
8、如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出? [??? ].
A.2个??? B.4个??? C.6个??? D.8个
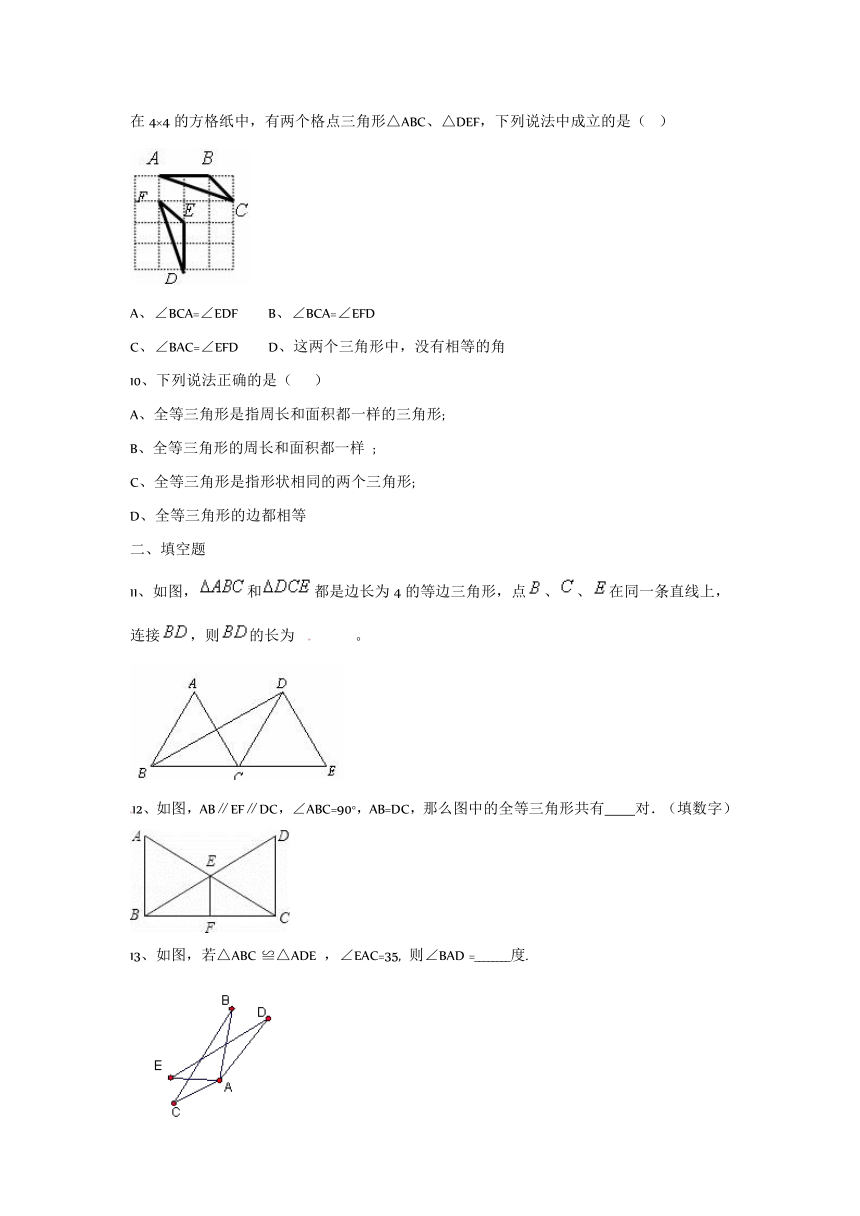
9、方格纸中,每个小格顶点叫做一个格点,以格点连线为边的三角形叫做格点三角形.如图,在4×4的方格纸中,有两个格点三角形△ABC、△DEF,下列说法中成立的是(? )
A、∠BCA=∠EDF B、∠BCA=∠EFD
C、∠BAC=∠EFD D、这两个三角形中,没有相等的角
10、下列说法正确的是(??? )
A、全等三角形是指周长和面积都一样的三角形;
B、全等三角形的周长和面积都一样 ;
C、全等三角形是指形状相同的两个三角形;
D、全等三角形的边都相等
二、填空题
11、如图,和都是边长为4的等边三角形,点、、在同一条直线上,连接,则的长为?????????????。
??????????
12、如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中的全等三角形共有 对.(填数字)
13、如图,若△ABC ≌△ADE ,∠EAC=35, 则∠BAD =________度.
14、如图,△ABC的三个顶点分别在格子的3个顶点上,请你试着再在图中的格子的顶点上找出一个点,使得△DBC与△ABC全等,这样的三角形有? ????????????个.
15、如图12,铁路上A,B两站(视为线上两点)相距25千米,C,D为铁路同旁两个村庄(视为两点),DA⊥AB于A点,CB⊥AB于B点,DA=15千米,CB=10千米,现在要在铁路AB上修一个土特品回购站E,使C,D两村庄到E站的距离相等,则E站应建在距A站______千米处.?????????????????????????????????????????图
16、如图,等腰直角三角形ABC的直角顶点B在直线PQ上,AD⊥PQ于D,CE⊥PQ于E,且AD=2cm,DB=4cm,则梯形ADEC的面积是 _____.
17、(动手操作实验题)如图所示是小明自制对顶角的“小仪器”示意图:
(1)将直角三角板ABC的AC边延长且使AC固定;
(2)另一个三角板CDE的直角顶点与前一个三角板直角顶点重合;
(3)延长DC,∠PCD与∠ACF就是一组对顶角,已知∠1=30°,∠ACF为多少?
18、将两块直角三角尺的直角顶点重合为如图17的位置, 若∠AOD=110°,则∠BOC=____°
三、简答题
19、一张矩形纸片沿对角线剪开,得到两张三角形纸片,再将两张三角形纸片摆成如图18的形式,使点B,F,C, D在同一条直线上.
(1)你能说明AB⊥DE吗?
(2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予说明.
20、如图,已知M在AB上,BC=BD,MC=MD.请说明:AC=AD.
21、如图18,在△ABC中,点D在AB上,BD=BE,
(1)请你再添加一个条件,使得△BEA≌△BDC,并说明理由,你添加的条件是
理由是:
(2)根据你添加的条件,再写出图中的一对全等三角形
(只要求写出一对全等三角形,不再添加其它线段,不再标注或使用其它字母,不必说明理由。)
22、如图,AC=AD,∠BAC=∠BAD,点E在AB上.
(1)你能找出 ? 对全等的三角形;
(2)请写出一对全等三角形,并证明.
23、如图,△ABC中,AB=AC,中线BD和中线CE相交于点P,PB与PC相等吗?请说明你的理由.
24、?如图,在△ABC中,AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,求证:AD⊥EF。
25、如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
(1)试说明△BEC≌△DEC;
(2)延长BE,交AD 于F,BED=1200时,求EFD的度数.
四、计算题
26、如图, E、F、G分别是等边△ABC的边AB、BC、AC的中点.
(1) 图中有多少个三角形?
(2) 指出图中一对全等三角形,并给出证明.
27、如图,在△ABC中,AB = AC,点D、E分别是AB、AC的中点,点F是BE、CD的交点,请写出图中两组全等的三角形,并选出其中一组加以证明.
(要求:写出证明过程中的重要依据)
参考答案
一、选择题
1、A.
2、B
3、D
4、C
5、B
6、?D
7、C
8、B
9、B
10、B
二、填空题
11、
12、3对.
13、35
14、3
15、10.
16、18
17、?∠ACF=60°
18、_70°
三、简答题
19、 (1)由已知条件,易得△ABC≌△DEF,则有∠A=∠D;又∠ANP=∠DNC,所以∠APN=∠DCN=90°,即AB⊥DE.
(2)答案不惟一:由(1)可得∠BPD=∠EFD=90°,又PB=BC和∠PBD=∠ABC,依据“A,S,A”有△PBD≌△CBA.由此,还可得出△PEM≌△FBM及△PAN≌△CDN.
20、说明:△BCM≌△BDM
△ABC≌△ABDAC=AD.
21、答案不惟一,添加条件可以是:BA=BC;∠AEB=∠CDB;∠BAC=∠BCA;
∠BCD=∠BAE等等;现以添加条件∠AEB=∠CDB为例,理由如下:
因为∠AEB=∠CDB,BE=BD,∠B=∠B,所以△BEA≌△BDC(ASA)
另一对全等的三角形是△ADF≌△CEF或△AEC≌△CDA
22、解:(1)△ABC≌△ABD(SAS),△BCE≌△BED,△ACE≌△AED,故有3对.
(2)△ABC≌△ABD,
证明:在△ABC和△ABD中,
AC=AD,∠BAC=∠BAD,AB=AB,
∴△ABC≌△ABD(SAS).
23、?? 解:PB=PC
∵BD、CE是△ABC的中线
∴BE=AB ,DC=AC
∵AB=AC
∴BE =DC
又∵AB=AC
∴∠ABC=∠ACB
在△EBC与△DCB中? EB=DC ∠ABC=∠ACB? BC=BC
∴△EBC≌△DCB(SAS)
∴∠ECB=∠DBC?? ∴PB=PC
24、证明:∵AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,∴DE=DF。(2分)
在Rt△AED与Rt△AFD中,
∴Rt△AEDRt△AFD(HL)。(4分)
∴AE=AF,又AD是∠BAC的平分线,∴AD⊥EF。(5分)
25、
四、计算题
26、解:(1)图中共有5个三角形;
(2)△≌△.
∵ △是等边三角形,∴ ∠∠.
∵ 、、是边、、的中点,
∴AE=AG=CG=CF=AB.
∴ △≌△.
27、解:△ABE≌△ACD,△BCD≌△CBE或△BFD≌△CFE(写出两个即可)
(1)选△ABE≌△ACD
证明:∵点D、E分别是AB、AC的中点,
∴AD=AB,AE=AC
又∵AB=AC,∴AD=AE
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS)
(2)选△BCD≌△CBE
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角)
∵点D、E分别是AB、AC的中点,∴BD=AB,CE=AC,∴BD=CE
在△BCD和△CBE中,
∴△BCD≌△CBE
(3)选△BFD≌△CFE
方法一:
证明:∵点D、E分别是AB、AC的中点,
∴AD=AB,AE=AC
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS)
∴∠ABE=∠ACD(全等三角形对应角相等)
∵点D、E分别是AB、AC的中点,
∴BD=AB,CE=AC,
∴BD=CE
在△BFD和△CFE中,
∴△BFD≌△CFE(AAS)
方法二:
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角)
∵点D、E分别是AB、AC的中点,∴BD=AB,CE=AC,∴BD=CE
在△BCD和△CBE中,
∴△BCD≌△CBE(SAS)
∴∠BDC=∠CEB(全等三角形对应角相等)
∴△BFD≌△CFE(AAS)
姓名:_______________班级:_______________考号:_______________
一、选择题
1、如图,△ABC与△BDE都是等边三角形,AB
A.PO B.PQ??????? C.MO D.MQ
3、如图,D、E、F是△ABC三边的中点,且DE∥AB,DF∥AC,EF ∥BC, 平移△AEF可以得到的三角形是(????? )
A.△BDF???? B.△DEF???? C.△CDE???? D.△BDF和△CDE
4、如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD??? B.∠BAC=∠DAC? C.∠BCA=∠DCA? D.∠B=∠D=90°
5、如图,△ABC≌△DCB,若∠A=80°,∠ACB=40°,则∠BCD等于( ???)
A.80°? B.60°? C.40°? D.20°
6、下列两个三角形中,一定全等的是( ???)
A. 两个等边三角形
B. 有一个角是40°,腰相等的两个等腰三角形
C. 有一条边相等,有一个内角相等的两个等腰三角形
D. 有一个角是100°,底相等的两个等腰三角形
7、下列说法:①有两条直角边对应相等的两个直角三角形全等;②有斜边对应相等的两个等腰直角三角形全等;③有一条直角边和斜边上的高对应相等的两个直角三角形全等;
④有一条边相等的两个等腰直角三角形全等.其中正确的有(?? ).
A、1个 B、2个 C、3个 D、4个
8、如图,△ABC是不等边三角形,DE=BC,以D、E为两个顶点作位置不同的三角形,使所作三角形与△ABC全等,这样的三角形最多可以画出? [??? ].
A.2个??? B.4个??? C.6个??? D.8个
9、方格纸中,每个小格顶点叫做一个格点,以格点连线为边的三角形叫做格点三角形.如图,在4×4的方格纸中,有两个格点三角形△ABC、△DEF,下列说法中成立的是(? )
A、∠BCA=∠EDF B、∠BCA=∠EFD
C、∠BAC=∠EFD D、这两个三角形中,没有相等的角
10、下列说法正确的是(??? )
A、全等三角形是指周长和面积都一样的三角形;
B、全等三角形的周长和面积都一样 ;
C、全等三角形是指形状相同的两个三角形;
D、全等三角形的边都相等
二、填空题
11、如图,和都是边长为4的等边三角形,点、、在同一条直线上,连接,则的长为?????????????。
??????????
12、如图,AB∥EF∥DC,∠ABC=90°,AB=DC,那么图中的全等三角形共有 对.(填数字)
13、如图,若△ABC ≌△ADE ,∠EAC=35, 则∠BAD =________度.
14、如图,△ABC的三个顶点分别在格子的3个顶点上,请你试着再在图中的格子的顶点上找出一个点,使得△DBC与△ABC全等,这样的三角形有? ????????????个.
15、如图12,铁路上A,B两站(视为线上两点)相距25千米,C,D为铁路同旁两个村庄(视为两点),DA⊥AB于A点,CB⊥AB于B点,DA=15千米,CB=10千米,现在要在铁路AB上修一个土特品回购站E,使C,D两村庄到E站的距离相等,则E站应建在距A站______千米处.?????????????????????????????????????????图
16、如图,等腰直角三角形ABC的直角顶点B在直线PQ上,AD⊥PQ于D,CE⊥PQ于E,且AD=2cm,DB=4cm,则梯形ADEC的面积是 _____.
17、(动手操作实验题)如图所示是小明自制对顶角的“小仪器”示意图:
(1)将直角三角板ABC的AC边延长且使AC固定;
(2)另一个三角板CDE的直角顶点与前一个三角板直角顶点重合;
(3)延长DC,∠PCD与∠ACF就是一组对顶角,已知∠1=30°,∠ACF为多少?
18、将两块直角三角尺的直角顶点重合为如图17的位置, 若∠AOD=110°,则∠BOC=____°
三、简答题
19、一张矩形纸片沿对角线剪开,得到两张三角形纸片,再将两张三角形纸片摆成如图18的形式,使点B,F,C, D在同一条直线上.
(1)你能说明AB⊥DE吗?
(2)若PB=BC,请找出图中与此条件有关的一对全等三角形,并给予说明.
20、如图,已知M在AB上,BC=BD,MC=MD.请说明:AC=AD.
21、如图18,在△ABC中,点D在AB上,BD=BE,
(1)请你再添加一个条件,使得△BEA≌△BDC,并说明理由,你添加的条件是
理由是:
(2)根据你添加的条件,再写出图中的一对全等三角形
(只要求写出一对全等三角形,不再添加其它线段,不再标注或使用其它字母,不必说明理由。)
22、如图,AC=AD,∠BAC=∠BAD,点E在AB上.
(1)你能找出 ? 对全等的三角形;
(2)请写出一对全等三角形,并证明.
23、如图,△ABC中,AB=AC,中线BD和中线CE相交于点P,PB与PC相等吗?请说明你的理由.
24、?如图,在△ABC中,AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,求证:AD⊥EF。
25、如图,在正方形ABCD中,AC为对角线,E为AC上一点,连接EB、ED.
(1)试说明△BEC≌△DEC;
(2)延长BE,交AD 于F,BED=1200时,求EFD的度数.
四、计算题
26、如图, E、F、G分别是等边△ABC的边AB、BC、AC的中点.
(1) 图中有多少个三角形?
(2) 指出图中一对全等三角形,并给出证明.
27、如图,在△ABC中,AB = AC,点D、E分别是AB、AC的中点,点F是BE、CD的交点,请写出图中两组全等的三角形,并选出其中一组加以证明.
(要求:写出证明过程中的重要依据)
参考答案
一、选择题
1、A.
2、B
3、D
4、C
5、B
6、?D
7、C
8、B
9、B
10、B
二、填空题
11、
12、3对.
13、35
14、3
15、10.
16、18
17、?∠ACF=60°
18、_70°
三、简答题
19、 (1)由已知条件,易得△ABC≌△DEF,则有∠A=∠D;又∠ANP=∠DNC,所以∠APN=∠DCN=90°,即AB⊥DE.
(2)答案不惟一:由(1)可得∠BPD=∠EFD=90°,又PB=BC和∠PBD=∠ABC,依据“A,S,A”有△PBD≌△CBA.由此,还可得出△PEM≌△FBM及△PAN≌△CDN.
20、说明:△BCM≌△BDM
△ABC≌△ABDAC=AD.
21、答案不惟一,添加条件可以是:BA=BC;∠AEB=∠CDB;∠BAC=∠BCA;
∠BCD=∠BAE等等;现以添加条件∠AEB=∠CDB为例,理由如下:
因为∠AEB=∠CDB,BE=BD,∠B=∠B,所以△BEA≌△BDC(ASA)
另一对全等的三角形是△ADF≌△CEF或△AEC≌△CDA
22、解:(1)△ABC≌△ABD(SAS),△BCE≌△BED,△ACE≌△AED,故有3对.
(2)△ABC≌△ABD,
证明:在△ABC和△ABD中,
AC=AD,∠BAC=∠BAD,AB=AB,
∴△ABC≌△ABD(SAS).
23、?? 解:PB=PC
∵BD、CE是△ABC的中线
∴BE=AB ,DC=AC
∵AB=AC
∴BE =DC
又∵AB=AC
∴∠ABC=∠ACB
在△EBC与△DCB中? EB=DC ∠ABC=∠ACB? BC=BC
∴△EBC≌△DCB(SAS)
∴∠ECB=∠DBC?? ∴PB=PC
24、证明:∵AD是∠BAC的平分线,DE、DF分别是△ABD和△ACD的高线,∴DE=DF。(2分)
在Rt△AED与Rt△AFD中,
∴Rt△AEDRt△AFD(HL)。(4分)
∴AE=AF,又AD是∠BAC的平分线,∴AD⊥EF。(5分)
25、
四、计算题
26、解:(1)图中共有5个三角形;
(2)△≌△.
∵ △是等边三角形,∴ ∠∠.
∵ 、、是边、、的中点,
∴AE=AG=CG=CF=AB.
∴ △≌△.
27、解:△ABE≌△ACD,△BCD≌△CBE或△BFD≌△CFE(写出两个即可)
(1)选△ABE≌△ACD
证明:∵点D、E分别是AB、AC的中点,
∴AD=AB,AE=AC
又∵AB=AC,∴AD=AE
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS)
(2)选△BCD≌△CBE
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角)
∵点D、E分别是AB、AC的中点,∴BD=AB,CE=AC,∴BD=CE
在△BCD和△CBE中,
∴△BCD≌△CBE
(3)选△BFD≌△CFE
方法一:
证明:∵点D、E分别是AB、AC的中点,
∴AD=AB,AE=AC
在△ABE和△ACD中,
∴△ABE≌△ACD(SAS)
∴∠ABE=∠ACD(全等三角形对应角相等)
∵点D、E分别是AB、AC的中点,
∴BD=AB,CE=AC,
∴BD=CE
在△BFD和△CFE中,
∴△BFD≌△CFE(AAS)
方法二:
证明:∵AB=AC,
∴∠ABC=∠ACB(等边对等角)
∵点D、E分别是AB、AC的中点,∴BD=AB,CE=AC,∴BD=CE
在△BCD和△CBE中,
∴△BCD≌△CBE(SAS)
∴∠BDC=∠CEB(全等三角形对应角相等)
∴△BFD≌△CFE(AAS)
