11.3角的平分线的性质课时作业(附答案)
文档属性
| 名称 | 11.3角的平分线的性质课时作业(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 118.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-04 15:06:16 | ||
图片预览



文档简介
11.3角的平分线的性质课时作业(附答案)
姓名:_______________班级:_______________考号:_______________
一、选择题
1、如图, △ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:①AD上任意一点到点C、点B的距离相等;②AD上任意一点到AB、AC的距离相等;③AD⊥BC且BD=CD;④∠BDE=∠CDF其中正确的个数是?????(?????? )
A.1个???? B.2个? ???? C.3个????? D.4个
2、如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,则下列五个结论:①AD上任意一点到AB、AC两边的距离相等;②AD上任意一点到B、C两点的距离相等;③AD⊥BC,且BD=CD;④∠BDE=∠CDF;
⑤AE=AF.其中,正确的有(? ??)
A、2个????? B、3个???? C、4个??? D、5个
3、如图,在△ABC与△ADB中,∠ACB=∠ADB=90°,E为AB中点,若AB=8,DC=7,则△CDE的周长是?? (??? )
A.21???????????? B.18??????????? ???C.13???????????? D.15
4、?到三角形三边的距离都相等的点是这个三角形的 ?????? (??? )
A.三条角平分线的交点??????? ? ? B.三条高的交点?
C.三条边的垂直平分线的交点??? D.三条中线的交点
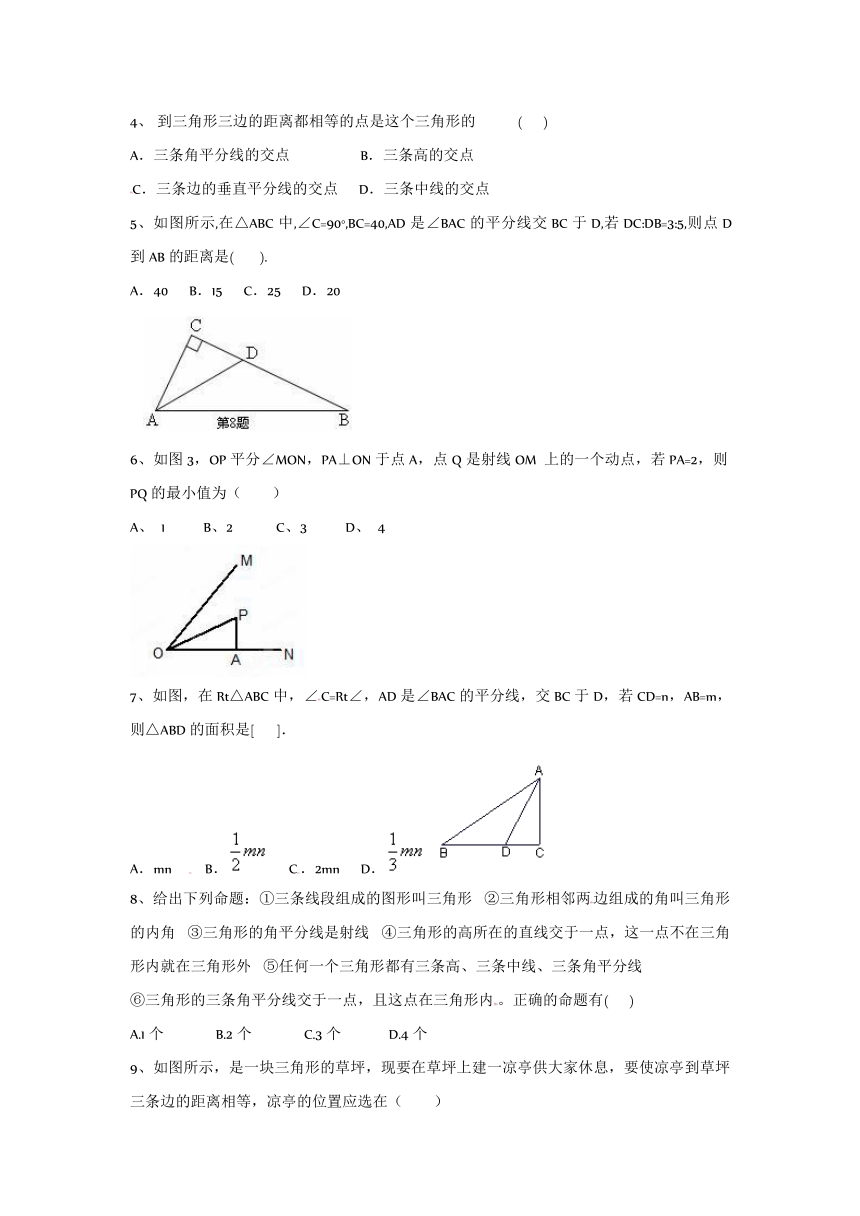
5、如图所示,在△ABC中,∠C=90°,BC=40,AD是∠BAC的平分线交BC于D,若DC:DB=3:5,则点D到AB的距离是(???? ).
A.40??? B.15??? C.25??? D.20
6、如图3,OP平分∠MON,PA⊥ON于点A,点Q是射线OM 上的一个动点,若PA=2,则PQ的最小值为(????? )
A、 1??????? B、2???????? C、3??????? D、 4
7、如图,在Rt△ABC中,∠C=Rt∠,AD是∠BAC的平分线,交BC于D,若CD=n,AB=m,则△ABD的面积是[??? ].
A.mn???????B.??? C.2mn??? D.
8、给出下列命题:①三条线段组成的图形叫三角形? ②三角形相邻两边组成的角叫三角形的内角? ③三角形的角平分线是射线? ④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外? ⑤任何一个三角形都有三条高、三条中线、三条角平分线
⑥三角形的三条角平分线交于一点,且这点在三角形内。正确的命题有(??? )
A.1个?????????? B.2个?????????? C.3个????????? D.4个
9、如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点 B.△ABC三边的中垂线的交点
C. △ABC三条高所在直线的交点 D. △ABC三条角平分线的交点
10、如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是(?? )
A、10cm??? B、15cm?? C、20cm??? D、25cm
二、填空题
11、如图把Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折痕ED,再沿BE折叠,C点恰好与D点重合,则∠A等于_______度.
12、如图,△ABC中,=90°,AD平分,交BC于点D,已知AB=10cm,CD=3cm,则△ABD的面积为
13、已知:如图,在△ABC中,∠C=90°,AD平分∠BAC,2CD=BD,BC=6,则点D到AB边的距离是????????????? .
14、?如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m和8m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是?????????? ??。
15、如图7,等腰直角三角形ABC的直角顶点B在直线PQ上,AD⊥PQ于D,CE⊥PQ于E,且AD=2厘米,DB=4厘米,则梯形ADEC的面积是 _____.
16、如图,Rt△ABC中,∠ACB=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是??????????? ??????。
17、如图,∠C=90°,∠1=∠2,若BC=10,BD=6,则D到AB的距离为_______.
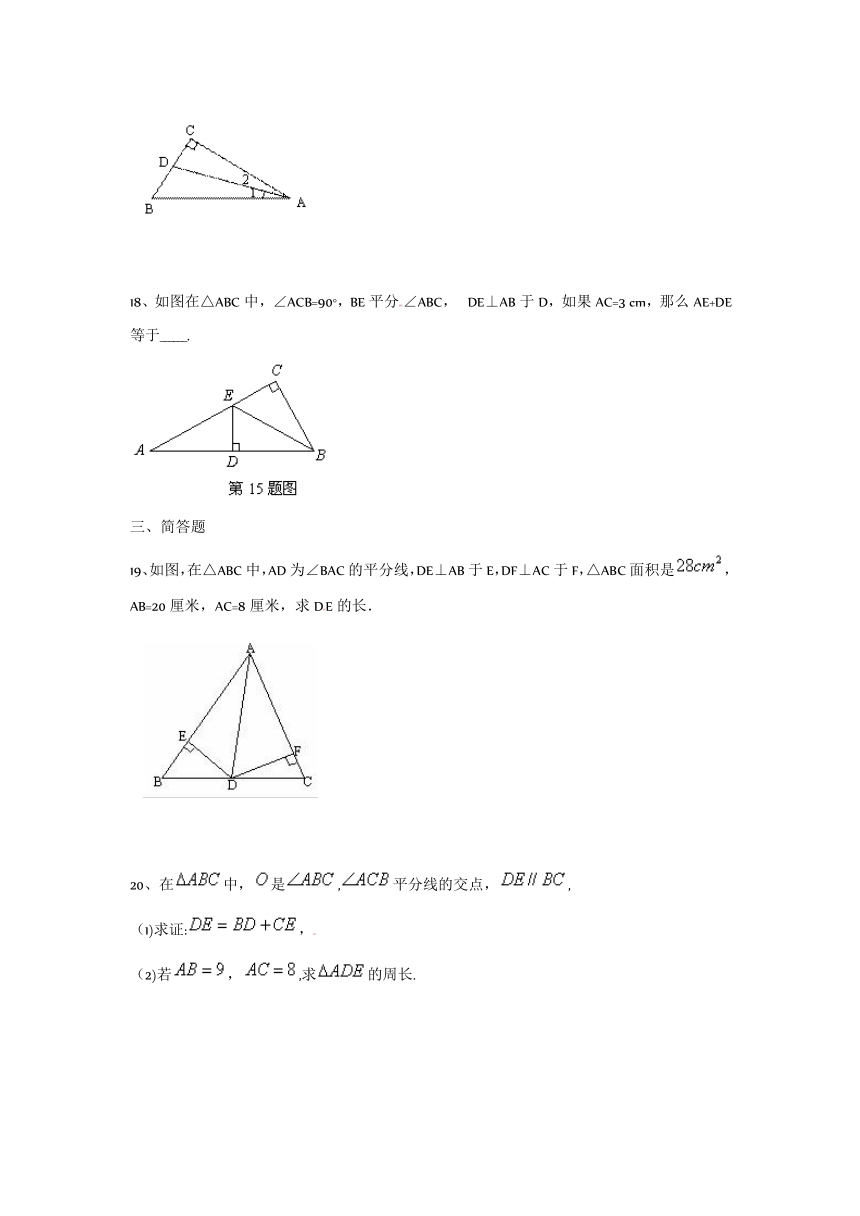
18、如图在△ABC中,∠ACB=90°,BE平分∠ABC,? DE⊥AB于D,如果AC=3 cm,那么AE+DE等于______.
三、简答题
19、如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是,AB=20厘米,AC=8厘米,求DE的长.
20、在中,是,平分线的交点,,
(1)求证:,
(2)若,,求的周长.
21、如图,已知:∠AOP=∠BOP,PC∥OA,PD⊥OA,若PC=6,PD = 4
(1)?????? 求证:OC=CP
(2)?????? 求△OCP的面积
22、已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.
23、1)在图28-1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:①DC = BC; ②AD+AB=AC.请你证明结论②;
(2) 在图28-2中,把(1)中的条件“∠ABC=∠ADC=90°”
改为∠ABC+∠ADC=180°
其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
24、如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;(2) 连接OA,BC,求证:直线OA⊥BC
25、已知,如图,AB=BC,DE=BE,且∠B=90°,ED⊥AC于D,求证:∠EAD=∠C.(8分)
四、计算题
26、如图,在梯形ABCD中,AB∥CD,∠BCD=90°,且AB=1,BC=2,tan∠ADC=2.
(1) 求证:DC=BC;
(2) E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
五、综合题
27、?(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:① DC = BC; ②AD+AB=AC.请你证明结论②;
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
参考答案
一、选择题
1、D
2、?D
3、D
4、A
5、B,
6、B
7、B
8、?B
9、D
10、C
二、填空题
11、?30
12、15平方厘米
13、?2 ;
14、6
15、18平方厘米;
16、?5
17、?4
18、3 ;
三、简答题
19、DE=2厘米
20、解:如图,是角平分线,∴ ???,
又
∴,则
∴是等? 腰三角形,∴
同理可证 ∴
周长为:
21、本题共10分, (1)5分,(2) 5分)
(1)略
(2)过P点作OB的垂线段,S⊿OCP =6×4÷2=12
22、
23、
24、(1)(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴ △ACD≌△ABE.
∴ AD=AE.? ????
(2) 在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,∴ △ADO≌△AEO.
∴ ∠DAO=∠EAO.
即OA是∠BAC的平分线.
又∵AB=AC,
∴ OA⊥BC.
25、∵AB=BC
∴∠BAC=∠C
∵DE=BE,且∠B=90°,DE⊥AC
∴∠EAD=∠BAC
∴∠EAD=∠C
四、计算题
26、解(1)过A作DC的垂线AM交DC于M,则AM=BC=2.
又∵tan∠ADC=2,? ∴DM=1.即DC=BC.
(2)等腰三角形.
证明:∵DE=DF,∠EDC=∠FBC,∠EDC=∠FBC,DC=BC.
∴△DEC≌△BFC
∴CE=CF,∠ECD=∠BCF.
∴∠ECF=∠BCF+∠BCE=∠ECD+∠BCE=∠BCD=900
即△ECF是等腰直角三角形.
五、综合题
27、(1)证明:
∵∠MAN=120°,AC平分∠MAN.
∴∠DAC = ∠BAC =600
∵∠ABC=∠ADC=90°,
∴∠DCA=∠BCA=30°,
在Rt△ACD,Rt△ACB中,∠DCA=30°
∠BCA=30°
∴AC=2AD,?? AC = 2AB,?
∴2AD=2AB
∴AD=AB??
∴AD+AB=AC.
(2)解:(1)中的结论① DC = BC; ②AD+AB=AC都成立,
理由一:如图2,在AN上截取AE=AC,连结CE,
∵∠BAC =60°,
∴△CAE为等边三角形,
∴AC=CE,∠AEC =60°,
∵∠DAC =60°,∴∠DAC =∠AEC,?
∵∠ABC+∠ADC=180°,∠ABC+∠EBC=180°,
∴∠ADC =∠EBC, ∴,
∴DC = BC,DA = BE,?
∴AD+AB=AB+BE=AE,?? ∴AD+AB=AC.
或者理由二:如图,过C作CE⊥AN,CF⊥AM于E、F
证明△BCE≌△DCF,得到
DC=BC,BE=DF
即AC=AE+AF=AB+AD亦可
得分参照理由一给分
姓名:_______________班级:_______________考号:_______________
一、选择题
1、如图, △ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F为垂足,则下列四个结论:①AD上任意一点到点C、点B的距离相等;②AD上任意一点到AB、AC的距离相等;③AD⊥BC且BD=CD;④∠BDE=∠CDF其中正确的个数是?????(?????? )
A.1个???? B.2个? ???? C.3个????? D.4个
2、如图,△ABC中,AB=AC,AD平分∠BAC,DE⊥AB于E,DF⊥AC于F,则下列五个结论:①AD上任意一点到AB、AC两边的距离相等;②AD上任意一点到B、C两点的距离相等;③AD⊥BC,且BD=CD;④∠BDE=∠CDF;
⑤AE=AF.其中,正确的有(? ??)
A、2个????? B、3个???? C、4个??? D、5个
3、如图,在△ABC与△ADB中,∠ACB=∠ADB=90°,E为AB中点,若AB=8,DC=7,则△CDE的周长是?? (??? )
A.21???????????? B.18??????????? ???C.13???????????? D.15
4、?到三角形三边的距离都相等的点是这个三角形的 ?????? (??? )
A.三条角平分线的交点??????? ? ? B.三条高的交点?
C.三条边的垂直平分线的交点??? D.三条中线的交点
5、如图所示,在△ABC中,∠C=90°,BC=40,AD是∠BAC的平分线交BC于D,若DC:DB=3:5,则点D到AB的距离是(???? ).
A.40??? B.15??? C.25??? D.20
6、如图3,OP平分∠MON,PA⊥ON于点A,点Q是射线OM 上的一个动点,若PA=2,则PQ的最小值为(????? )
A、 1??????? B、2???????? C、3??????? D、 4
7、如图,在Rt△ABC中,∠C=Rt∠,AD是∠BAC的平分线,交BC于D,若CD=n,AB=m,则△ABD的面积是[??? ].
A.mn???????B.??? C.2mn??? D.
8、给出下列命题:①三条线段组成的图形叫三角形? ②三角形相邻两边组成的角叫三角形的内角? ③三角形的角平分线是射线? ④三角形的高所在的直线交于一点,这一点不在三角形内就在三角形外? ⑤任何一个三角形都有三条高、三条中线、三条角平分线
⑥三角形的三条角平分线交于一点,且这点在三角形内。正确的命题有(??? )
A.1个?????????? B.2个?????????? C.3个????????? D.4个
9、如图所示,是一块三角形的草坪,现要在草坪上建一凉亭供大家休息,要使凉亭到草坪三条边的距离相等,凉亭的位置应选在( )
A.△ABC的三条中线的交点 B.△ABC三边的中垂线的交点
C. △ABC三条高所在直线的交点 D. △ABC三条角平分线的交点
10、如图,△ABC中,∠C=90°,AM平分∠CAB,CM=20cm,那么M到AB的距离是(?? )
A、10cm??? B、15cm?? C、20cm??? D、25cm
二、填空题
11、如图把Rt△ABC(∠C=90°)折叠,使A、B两点重合,得到折痕ED,再沿BE折叠,C点恰好与D点重合,则∠A等于_______度.
12、如图,△ABC中,=90°,AD平分,交BC于点D,已知AB=10cm,CD=3cm,则△ABD的面积为
13、已知:如图,在△ABC中,∠C=90°,AD平分∠BAC,2CD=BD,BC=6,则点D到AB边的距离是????????????? .
14、?如图是油路管道的一部分,延伸外围的支路恰好构成一个直角三角形,两直角边分别为6m和8m.按照输油中心O到三条支路的距离相等来连接管道,则O到三条支路的管道总长(计算时视管道为线,中心O为点)是?????????? ??。
15、如图7,等腰直角三角形ABC的直角顶点B在直线PQ上,AD⊥PQ于D,CE⊥PQ于E,且AD=2厘米,DB=4厘米,则梯形ADEC的面积是 _____.
16、如图,Rt△ABC中,∠ACB=90°,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是??????????? ??????。
17、如图,∠C=90°,∠1=∠2,若BC=10,BD=6,则D到AB的距离为_______.
18、如图在△ABC中,∠ACB=90°,BE平分∠ABC,? DE⊥AB于D,如果AC=3 cm,那么AE+DE等于______.
三、简答题
19、如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是,AB=20厘米,AC=8厘米,求DE的长.
20、在中,是,平分线的交点,,
(1)求证:,
(2)若,,求的周长.
21、如图,已知:∠AOP=∠BOP,PC∥OA,PD⊥OA,若PC=6,PD = 4
(1)?????? 求证:OC=CP
(2)?????? 求△OCP的面积
22、已知,如图,BD是∠ABC的平分线,AB=BC,点P在BD上,PM⊥AD,PN⊥CD,垂足分别是M、N.试说明:PM=PN.
23、1)在图28-1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:①DC = BC; ②AD+AB=AC.请你证明结论②;
(2) 在图28-2中,把(1)中的条件“∠ABC=∠ADC=90°”
改为∠ABC+∠ADC=180°
其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
24、如图 AB=AC,CD⊥AB于D,BE⊥AC于E,BE与CD相交于点O.
(1)求证AD=AE;(2) 连接OA,BC,求证:直线OA⊥BC
25、已知,如图,AB=BC,DE=BE,且∠B=90°,ED⊥AC于D,求证:∠EAD=∠C.(8分)
四、计算题
26、如图,在梯形ABCD中,AB∥CD,∠BCD=90°,且AB=1,BC=2,tan∠ADC=2.
(1) 求证:DC=BC;
(2) E是梯形内一点,F是梯形外一点,且∠EDC=∠FBC,DE=BF,试判断△ECF的形状,并证明你的结论;
五、综合题
27、?(1)在图1中,已知∠MAN=120°,AC平分∠MAN.∠ABC=∠ADC=90°,则能得如下两个结论:① DC = BC; ②AD+AB=AC.请你证明结论②;
(2)在图2中,把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
参考答案
一、选择题
1、D
2、?D
3、D
4、A
5、B,
6、B
7、B
8、?B
9、D
10、C
二、填空题
11、?30
12、15平方厘米
13、?2 ;
14、6
15、18平方厘米;
16、?5
17、?4
18、3 ;
三、简答题
19、DE=2厘米
20、解:如图,是角平分线,∴ ???,
又
∴,则
∴是等? 腰三角形,∴
同理可证 ∴
周长为:
21、本题共10分, (1)5分,(2) 5分)
(1)略
(2)过P点作OB的垂线段,S⊿OCP =6×4÷2=12
22、
23、
24、(1)(1)证明:在△ACD与△ABE中,
∵∠A=∠A,∠ADC=∠AEB=90°,AB=AC,
∴ △ACD≌△ABE.
∴ AD=AE.? ????
(2) 在Rt△ADO与△AEO中,
∵OA=OA,AD=AE,∴ △ADO≌△AEO.
∴ ∠DAO=∠EAO.
即OA是∠BAC的平分线.
又∵AB=AC,
∴ OA⊥BC.
25、∵AB=BC
∴∠BAC=∠C
∵DE=BE,且∠B=90°,DE⊥AC
∴∠EAD=∠BAC
∴∠EAD=∠C
四、计算题
26、解(1)过A作DC的垂线AM交DC于M,则AM=BC=2.
又∵tan∠ADC=2,? ∴DM=1.即DC=BC.
(2)等腰三角形.
证明:∵DE=DF,∠EDC=∠FBC,∠EDC=∠FBC,DC=BC.
∴△DEC≌△BFC
∴CE=CF,∠ECD=∠BCF.
∴∠ECF=∠BCF+∠BCE=∠ECD+∠BCE=∠BCD=900
即△ECF是等腰直角三角形.
五、综合题
27、(1)证明:
∵∠MAN=120°,AC平分∠MAN.
∴∠DAC = ∠BAC =600
∵∠ABC=∠ADC=90°,
∴∠DCA=∠BCA=30°,
在Rt△ACD,Rt△ACB中,∠DCA=30°
∠BCA=30°
∴AC=2AD,?? AC = 2AB,?
∴2AD=2AB
∴AD=AB??
∴AD+AB=AC.
(2)解:(1)中的结论① DC = BC; ②AD+AB=AC都成立,
理由一:如图2,在AN上截取AE=AC,连结CE,
∵∠BAC =60°,
∴△CAE为等边三角形,
∴AC=CE,∠AEC =60°,
∵∠DAC =60°,∴∠DAC =∠AEC,?
∵∠ABC+∠ADC=180°,∠ABC+∠EBC=180°,
∴∠ADC =∠EBC, ∴,
∴DC = BC,DA = BE,?
∴AD+AB=AB+BE=AE,?? ∴AD+AB=AC.
或者理由二:如图,过C作CE⊥AN,CF⊥AM于E、F
证明△BCE≌△DCF,得到
DC=BC,BE=DF
即AC=AE+AF=AB+AD亦可
得分参照理由一给分
