近三年(2019-2021)高考真题数学分类汇编专题07不等式(Word含答案解析)
文档属性
| 名称 | 近三年(2019-2021)高考真题数学分类汇编专题07不等式(Word含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 550.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 08:36:49 | ||
图片预览




文档简介
专题07 不等式
1.【2021年·全国乙卷(文)】若x,y满足约束条件则的最小值为( )
A.18 B.10 C.6 D.4
2.【2021年·浙江卷】若实数x,y满足约束条件,则的最小值是( )
A.-2 B. C. D.
3.【2021年·全国乙卷(理)】在区间与中各随机取1个数,则两数之和大于的概率为()
A. B. C. D.
4.【2019年·全国Ⅱ卷(理)】若,则()
A. B. C. D.
5.【2020年·浙江卷】已知,对于任意均有,则( )
A. B. C. D.
6.【2019年·全国Ⅲ卷(文)】记不等式组表示的平面区域为.命题;命题.下面给出了四个命题
①②③④
这四个命题中,所有真命题的编号是( )
A.①③ B.①② C.②③ D.③④
7.【2020年·浙江卷】若实数满足约束条件,则的取值范围是( )
A. B. C. D.
8.【2020年·新高考Ⅰ卷】(多选)已知,且,则( )
A. B.
C. D.
9.【2020年·全国Ⅰ卷(理)】若满足约束条件则的最大值为____________.
10.【2020年·全国Ⅲ卷(文)】若满足约束条件,则的最大值为_____.
11.【2019年·全国Ⅱ卷(文)】若变量满足约束条件则的最大值是______.
12.【2021年·上海卷】已知实数x,y满足,则的最大值为_____________.
13.【2020年·全国Ⅱ卷(文)】若x,y满足约束条件则的最大值是____.
14.【2020年·天津卷】已知,且,则的最小值为_________.
15.【2020年·江苏卷】已知,则的最小值是.
答案以及解析
1.答案:C
解析:本题考查线性规划的应用.作出不等式组所表示的可行域(图略),可以看出该可行域是由三点,,围成的三角形(包含边界),显然,当经过点时,z取最小值,故.
2.答案:B
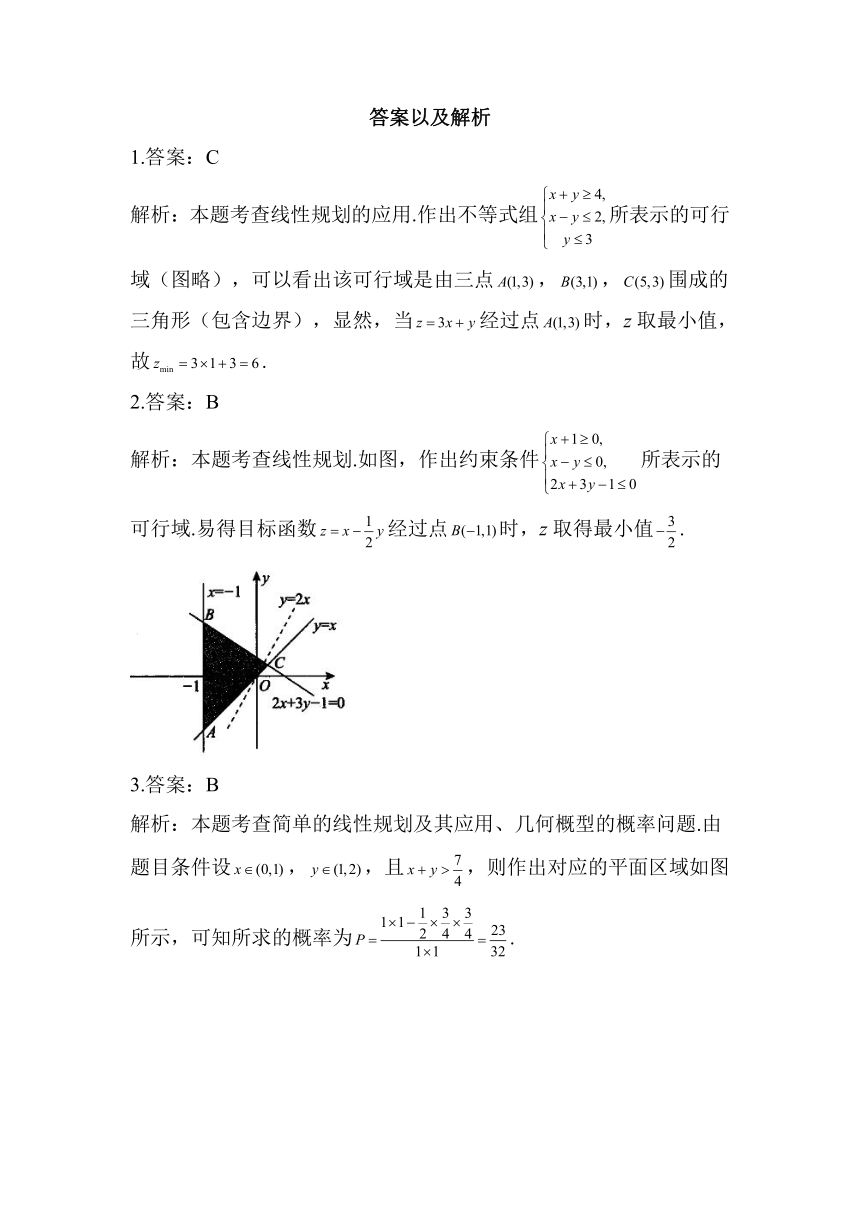
解析:本题考查线性规划.如图,作出约束条件所表示的可行域.易得目标函数经过点时,z取得最小值.
3.答案:B
解析:本题考查简单的线性规划及其应用、几何概型的概率问题.由题目条件设,,且,则作出对应的平面区域如图所示,可知所求的概率为.
4.答案:C
解析:取,满足,,知A错,排除A;
因为,知B错,排除B;
取,满足,,知D错,排除D,
因为幂函数是增函数,,所以,故选C.
5.答案:C
解析:解法一若互不相等,则当时,原不等式在时恒成立,又因为,所以;
若,则当时,原不等式在时恒成立,又因为,所以;
若,则当时,原不等式在时恒成立,又因为,所以;
若,则,与已知矛盾;
若,则,与已知矛盾.
综上,,故选C.
解法二特殊值法:当,时,在时恒成立;当,时,在时恒成立;当,时,在时不一定成立.故选C.
6.答案:A
解析:如图,平面区域D为阴影部分,由得即,直线与直线均过区域D,则p真q假,有假真,所以①③真②④假.故选A.
7.答案:B
解析:画出可行域如图中阴影部分所示,作出直线,平移该直线,易知当直线经过点时,取得最小值,,再数形结合可得的取值范围是.
8.答案:ABD
解析:对于选项A,,,,正确;对于选项B,易知,,,,正确;对于选项C,令,,则,错误;对于选项D,,,,正确.故选ABD.
9.答案:1
解析:通解作出可行域,如图中阴影部分所示,由得故.作出直线,数形结合可知,当直线过点时,取得最大值,为1.
优解作出可行域,如图中阴影部分所示,易得,,,当直线过点时,;当直线过点时,;当直线过点时,.所以的最大值为1.
10.答案:7
解析:解法一作出不等式组表示的平面区域如图中阴影部分所示,画出直线,平移该直线,由图可知当平移后的直线经过点时,取得最大值,.
解法二易知的最大值在可行域的顶点处取得,只需求出可行域的顶点坐标,分别将各顶点坐标代入,即可求得最大值.联立得解得代入中可得;联立得解得代入中可得;联立得解得代入中可得.通过比较可知,的最大值为7.
11.答案:9
解析:画出不等式组表示的可行域,如图所示,
阴影部分表示的区域,根据直线中的表示纵截距的相反数,当直线过点时,取最大值为9.
12.答案:4
解析:本题主要考查线性规划.根据题中所给约束条件可作出可行域如图所示,目标函数可化为,当z最大时,直线在y轴上的截距最小,由图可知当直线过直线和直线的交点时,截距最小,联立,解得,此时,所以z最大值为4.故本题正确答案为4.
13.答案:8
解析:解法一作出可行域如图中阴影部分所示,作出直线并平移,由图知,当平移后的直线经过点时,取得最大值,.
解法二易知可行域是一个封闭区域,因此目标函数的最值在区域的顶点处取得,由得此时;由得此时;由得此时.综上所述,的最大值为8.
14.答案:4
解析:依题意得,当且仅当即时取等号.因此,的最小值为4.
15.答案:
解析:解法一由得,则,当且仅当,即时取等号,则的最小值是.
解法二,则,当且仅当,即,时取等号,则的最小值是.
1.【2021年·全国乙卷(文)】若x,y满足约束条件则的最小值为( )
A.18 B.10 C.6 D.4
2.【2021年·浙江卷】若实数x,y满足约束条件,则的最小值是( )
A.-2 B. C. D.
3.【2021年·全国乙卷(理)】在区间与中各随机取1个数,则两数之和大于的概率为()
A. B. C. D.
4.【2019年·全国Ⅱ卷(理)】若,则()
A. B. C. D.
5.【2020年·浙江卷】已知,对于任意均有,则( )
A. B. C. D.
6.【2019年·全国Ⅲ卷(文)】记不等式组表示的平面区域为.命题;命题.下面给出了四个命题
①②③④
这四个命题中,所有真命题的编号是( )
A.①③ B.①② C.②③ D.③④
7.【2020年·浙江卷】若实数满足约束条件,则的取值范围是( )
A. B. C. D.
8.【2020年·新高考Ⅰ卷】(多选)已知,且,则( )
A. B.
C. D.
9.【2020年·全国Ⅰ卷(理)】若满足约束条件则的最大值为____________.
10.【2020年·全国Ⅲ卷(文)】若满足约束条件,则的最大值为_____.
11.【2019年·全国Ⅱ卷(文)】若变量满足约束条件则的最大值是______.
12.【2021年·上海卷】已知实数x,y满足,则的最大值为_____________.
13.【2020年·全国Ⅱ卷(文)】若x,y满足约束条件则的最大值是____.
14.【2020年·天津卷】已知,且,则的最小值为_________.
15.【2020年·江苏卷】已知,则的最小值是.
答案以及解析
1.答案:C
解析:本题考查线性规划的应用.作出不等式组所表示的可行域(图略),可以看出该可行域是由三点,,围成的三角形(包含边界),显然,当经过点时,z取最小值,故.
2.答案:B
解析:本题考查线性规划.如图,作出约束条件所表示的可行域.易得目标函数经过点时,z取得最小值.
3.答案:B
解析:本题考查简单的线性规划及其应用、几何概型的概率问题.由题目条件设,,且,则作出对应的平面区域如图所示,可知所求的概率为.
4.答案:C
解析:取,满足,,知A错,排除A;
因为,知B错,排除B;
取,满足,,知D错,排除D,
因为幂函数是增函数,,所以,故选C.
5.答案:C
解析:解法一若互不相等,则当时,原不等式在时恒成立,又因为,所以;
若,则当时,原不等式在时恒成立,又因为,所以;
若,则当时,原不等式在时恒成立,又因为,所以;
若,则,与已知矛盾;
若,则,与已知矛盾.
综上,,故选C.
解法二特殊值法:当,时,在时恒成立;当,时,在时恒成立;当,时,在时不一定成立.故选C.
6.答案:A
解析:如图,平面区域D为阴影部分,由得即,直线与直线均过区域D,则p真q假,有假真,所以①③真②④假.故选A.
7.答案:B
解析:画出可行域如图中阴影部分所示,作出直线,平移该直线,易知当直线经过点时,取得最小值,,再数形结合可得的取值范围是.
8.答案:ABD
解析:对于选项A,,,,正确;对于选项B,易知,,,,正确;对于选项C,令,,则,错误;对于选项D,,,,正确.故选ABD.
9.答案:1
解析:通解作出可行域,如图中阴影部分所示,由得故.作出直线,数形结合可知,当直线过点时,取得最大值,为1.
优解作出可行域,如图中阴影部分所示,易得,,,当直线过点时,;当直线过点时,;当直线过点时,.所以的最大值为1.
10.答案:7
解析:解法一作出不等式组表示的平面区域如图中阴影部分所示,画出直线,平移该直线,由图可知当平移后的直线经过点时,取得最大值,.
解法二易知的最大值在可行域的顶点处取得,只需求出可行域的顶点坐标,分别将各顶点坐标代入,即可求得最大值.联立得解得代入中可得;联立得解得代入中可得;联立得解得代入中可得.通过比较可知,的最大值为7.
11.答案:9
解析:画出不等式组表示的可行域,如图所示,
阴影部分表示的区域,根据直线中的表示纵截距的相反数,当直线过点时,取最大值为9.
12.答案:4
解析:本题主要考查线性规划.根据题中所给约束条件可作出可行域如图所示,目标函数可化为,当z最大时,直线在y轴上的截距最小,由图可知当直线过直线和直线的交点时,截距最小,联立,解得,此时,所以z最大值为4.故本题正确答案为4.
13.答案:8
解析:解法一作出可行域如图中阴影部分所示,作出直线并平移,由图知,当平移后的直线经过点时,取得最大值,.
解法二易知可行域是一个封闭区域,因此目标函数的最值在区域的顶点处取得,由得此时;由得此时;由得此时.综上所述,的最大值为8.
14.答案:4
解析:依题意得,当且仅当即时取等号.因此,的最小值为4.
15.答案:
解析:解法一由得,则,当且仅当,即时取等号,则的最小值是.
解法二,则,当且仅当,即,时取等号,则的最小值是.
同课章节目录
