七年数学专项复习系列之有理数的分类专项训练(含答案)
文档属性
| 名称 | 七年数学专项复习系列之有理数的分类专项训练(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 78.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 20:44:15 | ||
图片预览




文档简介
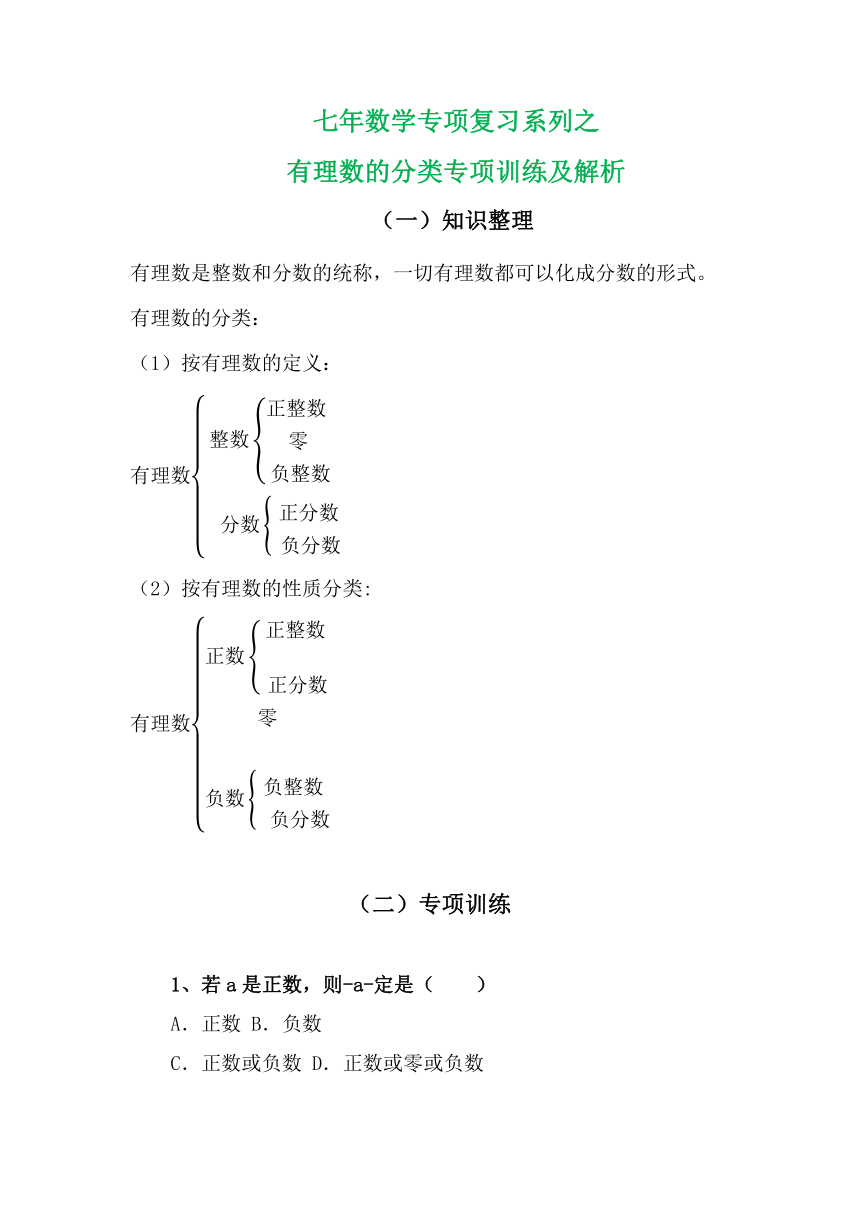
七年数学专项复习系列之
有理数的分类专项训练及解析
(一)知识整理
有理数是整数和分数的统称,一切有理数都可以化成分数的形式。
有理数的分类:
(1)按有理数的定义:
有理数
(2)按有理数的性质分类:
有理数
(二)专项训练
1、若a是正数,则-a-定是( )
A.正数 B.负数
C.正数或负数 D.正数或零或负数
【答案】∵a是正数,
∴-a-定是负数;
故选B.
2、把下列各数填在相应的大括号内:5,-2,1.4,0,-3.14159.
正数:{______};
非负整数:{______};
整数:{______};
负分数:{______}.
【答案】正数:{5,1.4};
非负整数:{5,0};
整数:{5,-2,0};
负分数:{,-3.14159}.
故答案为:5,1.4;5,0;5,-2,0;-3.14159.
3、将连续自然数1,2,3,…,n(n≥3)的排列顺序打乱,重新排列成a1,a2,a3,…,an.若(a1-1)(a2-2)(a3-3)…(an-n)恰为奇数,则( )
A.一定是偶数
B.一定是奇数
C.可能是奇数,也可能是偶数
D.一定是2m-1(m是奇数)
【答案】如果n是偶数的话,
在1~n这个数列中偶数的个数和奇数的个数相等,
要保证(a1-1)(a2-2)(a3-3)…(an-n)是奇数,则须保证每一项都为奇数.
因为a1~~an中奇数偶数都相等,
所以完全可能找出一队序列1~~n 使(a1-1)(a2-2)(a3-3)…(an-n)每一项都是奇数,
如果n是奇数的话,在1~n这个数列中偶数的个数比奇数的个数少一个,
要保证(a1-1)(a2-2)(a3-3)…(an-n)是奇数,则须保证每一项都为奇数.
因为a1~an中奇数比偶数多一个,一定会在(a1-1)(a2-2)(a3-3)…(an-n)中有一个偶数,
因此(a1-1)(a2-2)(a3-3)…(an-n)必为偶数,
所以n必为偶数.
故选A.
4、下列说法正确的是( )
A.一个数前面加上“-”号就是负数
B.互为相反数的两个数绝对值一定相等
C.正整数和负整数统称为整数
D.一个有理数的绝对值一定是正数
【答案】A、一个数前面加上“-”号就是负数不正确,例如-(-2)=2,是正数,故本选项错误;
B、互为相反数的两个数绝对值一定相等正确,故本选项正确;
C、应为正整数、零、负整数统称为整数,故本选项错误;
D、一个有理数的绝对值一定是正数错误,例如:0的绝对值是0,0既不是正数也不是负数,故本选项错误.
故选B.
5、下列说法正确的是( )
A.正数和负数互为相反数
B.任何有理数都有相反数
C.任何有理数都有倒数
D.a是有理数,-a是负有理数
【答案】A、例如:+1和-2不是相反数,故A错误;
B、有理数a的相反数是-a,故B正确;
C、0没有倒数,故C错误;
D、例如:-1是有理数,但-(-1)=1是正有理数,故D错误.
故选:B.
6、桌上有五枚硬币,每次操作,选择其中4个硬币并将它们翻转过来,即如果原来含国徽的一面朝上,将盖面朝下,原来含国徽的一面朝下,将该面朝上.如果开始的时候,五枚硬币有国徽的一面都朝上,你能经过若干次操作将这些硬币都翻转过来吗?如能,写出你的翻转过程,如不能,说明理由:
【答案】不可能.
假设用5个-1或者0表示,1表示国徽朝上,0表示国徽朝下.
开始时,由于5枚硬币全朝上,所以这5个数的和为0,是个偶数.一个硬币每翻动一次,所记数由0变为1,或由l变为0,改变了奇偶性.
每一次翻动四枚硬币,因此,5个之和的奇偶性仍与原来相同.
所以,不论翻动多少次,5个数之和仍为偶数.而5枚硬币全部朝下,和为5,是奇数,因此,不可能.
故答案为:不能.
7、任意写出5个负数,5个整数,5个正分数,5个有理数,并分别把写出的数填入下面所对应的集合中.
负数集合:{};
整数集合:{};
正分数集合:{};
有理数集合:{}.
【答案】负数集合:{-1,-π,-2.5,-0.3,- 2 5 …};
整数集合:{1,7,0,-2,-5…};
正分数集合:{ , ,0.3,1.5,,…};
有理数集合:{2,-3,0, 1 2 ,-1.2…}.
8、在-2,+3.5,0,-0.7,11中.负分数有( )
A.l个 B.2个 C.3个 D.4个
【答案】在这几个数中是负分数的有:-0.7.
故答案为:A.
9、在-π,-2,3.14,,,0.1414中,有理数的个数是( )
A.2个 B.3个 C.4个 D.5个
【答案】有理数有:-2,3.14,,0.1414共4个.
故选:C.
10、下列各数:-1,2.5,+ 4 3 ,0,-0.001,+2,-600中,正数有______,整数有______.
【答案】∵2.5>0, 4 3 >0,2>0,∴正数有2.5,+ 4 3 ,+2,
整数有-1,0,+2,-600.
故答案为:2.5,+ 4 3 +2;-1,0,+2,-600.
11、下列说法中:①最小的自然数是1;②最大的负数是-1;③没有最小的负数;④最小的整数是0.其中错误的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】∵最小的自然数是0,∴①错误;
∵最大的负整数是-1,没有最大的负数,∴②错误;
∵没有最小的负数,∴③正确;
∵没有最小的整数,∴④错误;
故选C.
12、把下列各数填在相应的横线上.
,-3.15,6,,-7,0,-100,0.4,78,π
(1)正整数:______
(2)整数:______
(3)负分数:______
(4)有理数:______.
(1)正整数:6,78;
(2)整数:6,-7,0,-100,78;
(3)负分数:-3.15;
(4)有理数:,-3.15,6,,-7,0,-100,0.4,78.
13、在数+8.3,-4,-0.8,0,90,- 1 5 ,- 34 3 ,-|-4|,π中,是正数的是______,整数的是______.
【答案】正数是:+8.3,90,π;
整数是:-4,0,90,-|-4|.
故答案为:+8.3,90,π;-4,0,90,-|-4|.
14、引入负数后,数的范围已扩充到有理数了.我们可以把有理数分为______和______.
【答案】有理数分为整数和分数.
故答案为:整数;分数.
15、有50位学生,男女各半,围坐一圈,是否存在一种座位的安排方法,使得每一位学生左右两侧的两位学生均为异性学生?请说明理由.
【答案】不存在这样的坐位安排.
反证之,若存在这样的坐位安排,则每一位学生必与一同性别同学相邻而坐,我们若以Y表示男性学生,以X表女性学生,
则如图所示,每一对相邻而坐的男性(女性)学生的左右两侧必为两对相邻而坐的女性(男性)学生,
这样50位学生共有25对相邻而坐的同性别学生.
25是一奇数,25对这样的学生中必有两对同为男性(女性)相邻,
即必有4位同性别学生依次相邻而坐,
从而与题意的要求矛盾.
所以这样的坐位安排方法是不存在的.
16、把下列各数填在相应的括号内:-8、4.5、-3.14、0、30%、-4、10、π
①自然数集合:{}
②整数集合:{}
③非正数集合:{}
④正分数集合:{}
⑤正有理数集合:{}.
【答案】①自然数集合:{0,10,…},
②整数集合:{0,-4,10,…},
③非正数集合:{-8、-3.14、0、-4,…},
④正分数集合:{4.5、30%,…},
⑤正有理数集合:{4.5、30%、10,…}.
17、把几个数用大括号围起来,中间用逗号断开,如:{1,2,-3},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数-a+10也必是这个集合的元素,这样的集合我们称为和谐的集合.例如集合{10,0}就是一个和谐集合.
(1)请你判断集合{-1,2},{-2,1,5,9,12}是不是和谐集合?
(2)请你再写出两个和谐的集合(至少有一个集合含有三个元素).
(3)写出所有和谐的集合中,元素个数最少的集合.
【答案】(1)若a=-1,则-a+10=11不在集合{-1,2}内,∴{-1,2}不是和谐集合.
∵-2+12=10,1+9=10,5+5=10,∴{-2,1,5,9,12}是和谐集合.
(2)根据和谐集合的定义可知a+10-a=10,只要集合中两个数之和为10即可,∵1+9=2+8=3+7=4+6,
∴{1,9,2,8}和{1,9,2,8,3,7}是和谐集合.
(3)∵5+5=10,
∴要使素个数最少,则集合{5},满足条件.
18、如图1,大、中、小三个圆圈分别表示有理数集合、整数集合、自然数集合,把这三个圆圈如图2所示叠放在一起,形成大圆环A和小圆环B,则小圆环B表示的是负整数集合.请你把下列各数填入图2相应的位置中,并写出大圆环A所表示的数的集合名称:-20、0、3.14、- 22 7 、5
【答案】大圆环A表示的集合为:分数集合.
19、下列表述正确的是( )
A.若一个数是分数,则它一定是有理数
B.不是正数的数一定是负数
C.有理数可分为正有理数、负有理数两大类
D.0不是整数
【答案】A、若一个数是分数,则它一定是有理数,正确;
B、不是正数的数一定是负数和0,故本选项错误;
C、有理数可分为正有理数、0,负有理数,故本选项错误;
D、0是整数,故本选项错误;
故选A.
20、将下列各有理数填入相应的集合内:- ,|- |,4,0,-27,0.36,+(-1.78)
整数:{…}负分数:{…}
正数:{…}负数:{…}.
【答案】整数:{4、0、-27…};
负分数:{- 、+(-1.78)…}
正数:{4、|- |、0.36…}
负数:{- 8 3 、-27、+(-1.78)…}.
有理数的分类专项训练及解析
(一)知识整理
有理数是整数和分数的统称,一切有理数都可以化成分数的形式。
有理数的分类:
(1)按有理数的定义:
有理数
(2)按有理数的性质分类:
有理数
(二)专项训练
1、若a是正数,则-a-定是( )
A.正数 B.负数
C.正数或负数 D.正数或零或负数
【答案】∵a是正数,
∴-a-定是负数;
故选B.
2、把下列各数填在相应的大括号内:5,-2,1.4,0,-3.14159.
正数:{______};
非负整数:{______};
整数:{______};
负分数:{______}.
【答案】正数:{5,1.4};
非负整数:{5,0};
整数:{5,-2,0};
负分数:{,-3.14159}.
故答案为:5,1.4;5,0;5,-2,0;-3.14159.
3、将连续自然数1,2,3,…,n(n≥3)的排列顺序打乱,重新排列成a1,a2,a3,…,an.若(a1-1)(a2-2)(a3-3)…(an-n)恰为奇数,则( )
A.一定是偶数
B.一定是奇数
C.可能是奇数,也可能是偶数
D.一定是2m-1(m是奇数)
【答案】如果n是偶数的话,
在1~n这个数列中偶数的个数和奇数的个数相等,
要保证(a1-1)(a2-2)(a3-3)…(an-n)是奇数,则须保证每一项都为奇数.
因为a1~~an中奇数偶数都相等,
所以完全可能找出一队序列1~~n 使(a1-1)(a2-2)(a3-3)…(an-n)每一项都是奇数,
如果n是奇数的话,在1~n这个数列中偶数的个数比奇数的个数少一个,
要保证(a1-1)(a2-2)(a3-3)…(an-n)是奇数,则须保证每一项都为奇数.
因为a1~an中奇数比偶数多一个,一定会在(a1-1)(a2-2)(a3-3)…(an-n)中有一个偶数,
因此(a1-1)(a2-2)(a3-3)…(an-n)必为偶数,
所以n必为偶数.
故选A.
4、下列说法正确的是( )
A.一个数前面加上“-”号就是负数
B.互为相反数的两个数绝对值一定相等
C.正整数和负整数统称为整数
D.一个有理数的绝对值一定是正数
【答案】A、一个数前面加上“-”号就是负数不正确,例如-(-2)=2,是正数,故本选项错误;
B、互为相反数的两个数绝对值一定相等正确,故本选项正确;
C、应为正整数、零、负整数统称为整数,故本选项错误;
D、一个有理数的绝对值一定是正数错误,例如:0的绝对值是0,0既不是正数也不是负数,故本选项错误.
故选B.
5、下列说法正确的是( )
A.正数和负数互为相反数
B.任何有理数都有相反数
C.任何有理数都有倒数
D.a是有理数,-a是负有理数
【答案】A、例如:+1和-2不是相反数,故A错误;
B、有理数a的相反数是-a,故B正确;
C、0没有倒数,故C错误;
D、例如:-1是有理数,但-(-1)=1是正有理数,故D错误.
故选:B.
6、桌上有五枚硬币,每次操作,选择其中4个硬币并将它们翻转过来,即如果原来含国徽的一面朝上,将盖面朝下,原来含国徽的一面朝下,将该面朝上.如果开始的时候,五枚硬币有国徽的一面都朝上,你能经过若干次操作将这些硬币都翻转过来吗?如能,写出你的翻转过程,如不能,说明理由:
【答案】不可能.
假设用5个-1或者0表示,1表示国徽朝上,0表示国徽朝下.
开始时,由于5枚硬币全朝上,所以这5个数的和为0,是个偶数.一个硬币每翻动一次,所记数由0变为1,或由l变为0,改变了奇偶性.
每一次翻动四枚硬币,因此,5个之和的奇偶性仍与原来相同.
所以,不论翻动多少次,5个数之和仍为偶数.而5枚硬币全部朝下,和为5,是奇数,因此,不可能.
故答案为:不能.
7、任意写出5个负数,5个整数,5个正分数,5个有理数,并分别把写出的数填入下面所对应的集合中.
负数集合:{};
整数集合:{};
正分数集合:{};
有理数集合:{}.
【答案】负数集合:{-1,-π,-2.5,-0.3,- 2 5 …};
整数集合:{1,7,0,-2,-5…};
正分数集合:{ , ,0.3,1.5,,…};
有理数集合:{2,-3,0, 1 2 ,-1.2…}.
8、在-2,+3.5,0,-0.7,11中.负分数有( )
A.l个 B.2个 C.3个 D.4个
【答案】在这几个数中是负分数的有:-0.7.
故答案为:A.
9、在-π,-2,3.14,,,0.1414中,有理数的个数是( )
A.2个 B.3个 C.4个 D.5个
【答案】有理数有:-2,3.14,,0.1414共4个.
故选:C.
10、下列各数:-1,2.5,+ 4 3 ,0,-0.001,+2,-600中,正数有______,整数有______.
【答案】∵2.5>0, 4 3 >0,2>0,∴正数有2.5,+ 4 3 ,+2,
整数有-1,0,+2,-600.
故答案为:2.5,+ 4 3 +2;-1,0,+2,-600.
11、下列说法中:①最小的自然数是1;②最大的负数是-1;③没有最小的负数;④最小的整数是0.其中错误的个数有( )
A.1个 B.2个 C.3个 D.4个
【答案】∵最小的自然数是0,∴①错误;
∵最大的负整数是-1,没有最大的负数,∴②错误;
∵没有最小的负数,∴③正确;
∵没有最小的整数,∴④错误;
故选C.
12、把下列各数填在相应的横线上.
,-3.15,6,,-7,0,-100,0.4,78,π
(1)正整数:______
(2)整数:______
(3)负分数:______
(4)有理数:______.
(1)正整数:6,78;
(2)整数:6,-7,0,-100,78;
(3)负分数:-3.15;
(4)有理数:,-3.15,6,,-7,0,-100,0.4,78.
13、在数+8.3,-4,-0.8,0,90,- 1 5 ,- 34 3 ,-|-4|,π中,是正数的是______,整数的是______.
【答案】正数是:+8.3,90,π;
整数是:-4,0,90,-|-4|.
故答案为:+8.3,90,π;-4,0,90,-|-4|.
14、引入负数后,数的范围已扩充到有理数了.我们可以把有理数分为______和______.
【答案】有理数分为整数和分数.
故答案为:整数;分数.
15、有50位学生,男女各半,围坐一圈,是否存在一种座位的安排方法,使得每一位学生左右两侧的两位学生均为异性学生?请说明理由.
【答案】不存在这样的坐位安排.
反证之,若存在这样的坐位安排,则每一位学生必与一同性别同学相邻而坐,我们若以Y表示男性学生,以X表女性学生,
则如图所示,每一对相邻而坐的男性(女性)学生的左右两侧必为两对相邻而坐的女性(男性)学生,
这样50位学生共有25对相邻而坐的同性别学生.
25是一奇数,25对这样的学生中必有两对同为男性(女性)相邻,
即必有4位同性别学生依次相邻而坐,
从而与题意的要求矛盾.
所以这样的坐位安排方法是不存在的.
16、把下列各数填在相应的括号内:-8、4.5、-3.14、0、30%、-4、10、π
①自然数集合:{}
②整数集合:{}
③非正数集合:{}
④正分数集合:{}
⑤正有理数集合:{}.
【答案】①自然数集合:{0,10,…},
②整数集合:{0,-4,10,…},
③非正数集合:{-8、-3.14、0、-4,…},
④正分数集合:{4.5、30%,…},
⑤正有理数集合:{4.5、30%、10,…}.
17、把几个数用大括号围起来,中间用逗号断开,如:{1,2,-3},我们称之为集合,其中的数称其为集合的元素.如果一个集合满足:当有理数a是集合的元素时,有理数-a+10也必是这个集合的元素,这样的集合我们称为和谐的集合.例如集合{10,0}就是一个和谐集合.
(1)请你判断集合{-1,2},{-2,1,5,9,12}是不是和谐集合?
(2)请你再写出两个和谐的集合(至少有一个集合含有三个元素).
(3)写出所有和谐的集合中,元素个数最少的集合.
【答案】(1)若a=-1,则-a+10=11不在集合{-1,2}内,∴{-1,2}不是和谐集合.
∵-2+12=10,1+9=10,5+5=10,∴{-2,1,5,9,12}是和谐集合.
(2)根据和谐集合的定义可知a+10-a=10,只要集合中两个数之和为10即可,∵1+9=2+8=3+7=4+6,
∴{1,9,2,8}和{1,9,2,8,3,7}是和谐集合.
(3)∵5+5=10,
∴要使素个数最少,则集合{5},满足条件.
18、如图1,大、中、小三个圆圈分别表示有理数集合、整数集合、自然数集合,把这三个圆圈如图2所示叠放在一起,形成大圆环A和小圆环B,则小圆环B表示的是负整数集合.请你把下列各数填入图2相应的位置中,并写出大圆环A所表示的数的集合名称:-20、0、3.14、- 22 7 、5
【答案】大圆环A表示的集合为:分数集合.
19、下列表述正确的是( )
A.若一个数是分数,则它一定是有理数
B.不是正数的数一定是负数
C.有理数可分为正有理数、负有理数两大类
D.0不是整数
【答案】A、若一个数是分数,则它一定是有理数,正确;
B、不是正数的数一定是负数和0,故本选项错误;
C、有理数可分为正有理数、0,负有理数,故本选项错误;
D、0是整数,故本选项错误;
故选A.
20、将下列各有理数填入相应的集合内:- ,|- |,4,0,-27,0.36,+(-1.78)
整数:{…}负分数:{…}
正数:{…}负数:{…}.
【答案】整数:{4、0、-27…};
负分数:{- 、+(-1.78)…}
正数:{4、|- |、0.36…}
负数:{- 8 3 、-27、+(-1.78)…}.
