人教版四年级下学期数学第三单元第2课时《加法运算定律的运用》教案(表格式)
文档属性
| 名称 | 人教版四年级下学期数学第三单元第2课时《加法运算定律的运用》教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 410.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 10:12:47 | ||
图片预览

文档简介
第三单元 运算定律
第2课时 加法运算定律的运用
教学内容分析:
本节课是学生在理解与掌握加法交换律和结合律的基础上学习的。运算定律的学习与简便计算是密不可分的,运算定律的学习让学生从原理上理解不同算法间的关系提供了可能,它是简便计算的基础。本节课是应用加法运算定律进行简便计算,从解决现实生活中的实际问题出发,关注计算方法的灵活性,使解决问题的策略更加多样化,有利于发展学生思维的灵活性,提高学生分析问题、解决问题的能力。
教学目标:
1. 引导学生在掌握和理解加法交换律和结合律的基础上,能运用运算定律进行一些简便运算。
2. 培养学生根据具体情况,选择算法的意识与能力,增强数感,发展思维的灵活性。
3. 能用所学的知识灵活解决实际问题,培养运用意识,感受数学与现实生活的联系。
教学重点:能运用运算定律进行简便运算。
教学难点:根据具体情况选择合适的算法进行简便计算。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 提问:上节课我们学习了什么? 生:加法交换律:a+b=b+a,改变加数的位置 加法结合律:(a+b)+c=a+(b+c)使用小括号,改变加法的运算顺序 从回顾上节课的学习内容引入新课学习。
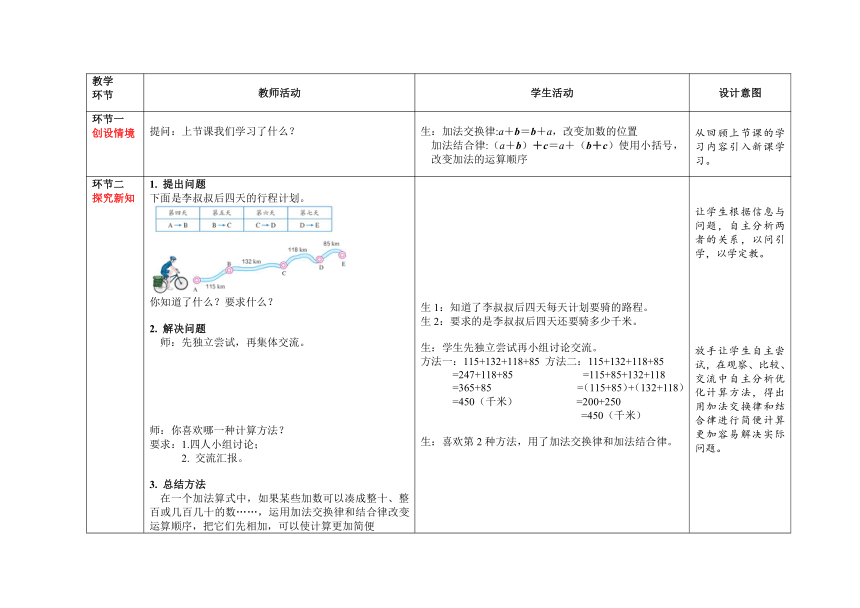
环节二 探究新知 提出问题 下面是李叔叔后四天的行程计划。 你知道了什么?要求什么? 解决问题 师:先独立尝试,再集体交流。 师:你喜欢哪一种计算方法? 要求:1.四人小组讨论; 交流汇报。 3. 总结方法 在一个加法算式中,如果某些加数可以凑成整十、整百或几百几十的数……,运用加法交换律和结合律改变运算顺序,把它们先相加,可以使计算更加简便 生1:知道了李叔叔后四天每天计划要骑的路程。 生2:要求的是李叔叔后四天还要骑多少千米。 生:学生先独立尝试再小组讨论交流。 方法一:115+132+118+85 方法二:115+132+118+85 =247+118+85 =115+85+132+118 =365+85 =(115+85)+(132+118) =450(千米) =200+250 =450(千米) 生:喜欢第2种方法,用了加法交换律和加法结合律。 让学生根据信息与问题,自主分析两者的关系,以问引学,以学定教。 放手让学生自主尝试,在观察、比较、交流中自主分析优化计算方法,得出用加法交换律和结合律进行简便计算更加容易解决实际问题。
环节三 巩固练习 1. 判断。(对的打“√”,错的画“×”) ⑴(a+178)+13=a +(178+13)运用了加法结合律。( ) ⑵ 63+34=34+63运用了加法交换律。( ) ⑶ 187+ a +13=187+13+ a只运用了加法交换律。( ) ⑷ 138+65+62=65+(138+62)只运用了加法交换律。( ) 2. 哪个算式计算最简便,把相应的字母填在( )内。 ⑴ 78+157+22 ( ) A 78+(157+22) B 157+(78+22) C (78+157)+22 ⑵ 91+43+109+57 ( ) A ( 91+43)+(109+57) B 91+(43+57)+109 C (91+109)+(43+57) 3. 王阿姨一共要汇多少钱? 4. 这堆原木一共有多少根? 师:说一说两种计算方法有什么不同? 生: (a +178)+13=a +(178+13)运用了加法结合律。(√) ⑵ 63+34=34+63运用了加法交换律。(√) ⑶ 187+ a +13=187+13+ a只运用了加法交换律。(√) ⑷ 138+65+62=65+(138+62)只运用了加法交换律。(×) 学生独立完成,汇报: 生1:B, 因为78+22=100,用加法结合律先相加更简便。 生2:C, 因为91+109=200,43+57=100,用加法结合律先相加更简便。 生: 225+328+175 =225+175+328 =400+328 =728(元) 答:王阿姨一共要汇728元。 生:方法一 方法二 生1:第一种方法是把能凑成整十的数结合先加。 生2:第二种方法是每两个数的和都等于第一个数与最后一个数的和,10个数中共有这样的5对。 进一步加深理解加法交换律与结合律的含义与作用。 根据数据特征把能凑成整十、整百、整千、几百几十……的数用加法交换律与结合律进行简便计算,培养数感,发展思维的灵活性。 该题是综合性运用加法交换律与结合律进行简便计算的知识,体现思维的灵活性。 方法二在加法交换律与结合律进行简便计算的基础上渗透等差数列求和的方法。
环节四 课堂小结 你有什么收获? 生1:加法交换律改变加数的位置,加法结合律使用小括号,改变加法的运算顺序,它们可以使计算更加简便。 生2:在计算加法时,要先观察数据的特点,运用加法的运算定律把可以凑成整十、整百、几百几十……的数先相加,可以使计算简便。: 鼓励学生自主整理知识,善于自我学习,提升学习力。
环节五 布置作业 教材P23练习六 第1、8、9题
环节六 拓展延伸 同学们,你们听说过数学家高斯小时候计算: 1+2+3+4+5+ …+99+100的和是多少的故事吗? 1+2+3+4+5+ …+99+100=? 微课视频 高斯这样解释: 因为1+100=101,2+99=101,3+98=101,…,49+52=101,50+51=101,而像这样和是101的组合一共有50组,所以很快就可以求出:101×50=5050。 =(1+100)+(2+99)+(3+98)+ +(50+51) =(1+100)×100÷2 =101×50 =5050 观看微课视频 分析方法 对学习有余力的学生进行拓展延伸,一方面开阔视野,另一方面发展数学思维,培养数学关键能力。
第2课时 加法运算定律的运用
教学内容分析:
本节课是学生在理解与掌握加法交换律和结合律的基础上学习的。运算定律的学习与简便计算是密不可分的,运算定律的学习让学生从原理上理解不同算法间的关系提供了可能,它是简便计算的基础。本节课是应用加法运算定律进行简便计算,从解决现实生活中的实际问题出发,关注计算方法的灵活性,使解决问题的策略更加多样化,有利于发展学生思维的灵活性,提高学生分析问题、解决问题的能力。
教学目标:
1. 引导学生在掌握和理解加法交换律和结合律的基础上,能运用运算定律进行一些简便运算。
2. 培养学生根据具体情况,选择算法的意识与能力,增强数感,发展思维的灵活性。
3. 能用所学的知识灵活解决实际问题,培养运用意识,感受数学与现实生活的联系。
教学重点:能运用运算定律进行简便运算。
教学难点:根据具体情况选择合适的算法进行简便计算。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 提问:上节课我们学习了什么? 生:加法交换律:a+b=b+a,改变加数的位置 加法结合律:(a+b)+c=a+(b+c)使用小括号,改变加法的运算顺序 从回顾上节课的学习内容引入新课学习。
环节二 探究新知 提出问题 下面是李叔叔后四天的行程计划。 你知道了什么?要求什么? 解决问题 师:先独立尝试,再集体交流。 师:你喜欢哪一种计算方法? 要求:1.四人小组讨论; 交流汇报。 3. 总结方法 在一个加法算式中,如果某些加数可以凑成整十、整百或几百几十的数……,运用加法交换律和结合律改变运算顺序,把它们先相加,可以使计算更加简便 生1:知道了李叔叔后四天每天计划要骑的路程。 生2:要求的是李叔叔后四天还要骑多少千米。 生:学生先独立尝试再小组讨论交流。 方法一:115+132+118+85 方法二:115+132+118+85 =247+118+85 =115+85+132+118 =365+85 =(115+85)+(132+118) =450(千米) =200+250 =450(千米) 生:喜欢第2种方法,用了加法交换律和加法结合律。 让学生根据信息与问题,自主分析两者的关系,以问引学,以学定教。 放手让学生自主尝试,在观察、比较、交流中自主分析优化计算方法,得出用加法交换律和结合律进行简便计算更加容易解决实际问题。
环节三 巩固练习 1. 判断。(对的打“√”,错的画“×”) ⑴(a+178)+13=a +(178+13)运用了加法结合律。( ) ⑵ 63+34=34+63运用了加法交换律。( ) ⑶ 187+ a +13=187+13+ a只运用了加法交换律。( ) ⑷ 138+65+62=65+(138+62)只运用了加法交换律。( ) 2. 哪个算式计算最简便,把相应的字母填在( )内。 ⑴ 78+157+22 ( ) A 78+(157+22) B 157+(78+22) C (78+157)+22 ⑵ 91+43+109+57 ( ) A ( 91+43)+(109+57) B 91+(43+57)+109 C (91+109)+(43+57) 3. 王阿姨一共要汇多少钱? 4. 这堆原木一共有多少根? 师:说一说两种计算方法有什么不同? 生: (a +178)+13=a +(178+13)运用了加法结合律。(√) ⑵ 63+34=34+63运用了加法交换律。(√) ⑶ 187+ a +13=187+13+ a只运用了加法交换律。(√) ⑷ 138+65+62=65+(138+62)只运用了加法交换律。(×) 学生独立完成,汇报: 生1:B, 因为78+22=100,用加法结合律先相加更简便。 生2:C, 因为91+109=200,43+57=100,用加法结合律先相加更简便。 生: 225+328+175 =225+175+328 =400+328 =728(元) 答:王阿姨一共要汇728元。 生:方法一 方法二 生1:第一种方法是把能凑成整十的数结合先加。 生2:第二种方法是每两个数的和都等于第一个数与最后一个数的和,10个数中共有这样的5对。 进一步加深理解加法交换律与结合律的含义与作用。 根据数据特征把能凑成整十、整百、整千、几百几十……的数用加法交换律与结合律进行简便计算,培养数感,发展思维的灵活性。 该题是综合性运用加法交换律与结合律进行简便计算的知识,体现思维的灵活性。 方法二在加法交换律与结合律进行简便计算的基础上渗透等差数列求和的方法。
环节四 课堂小结 你有什么收获? 生1:加法交换律改变加数的位置,加法结合律使用小括号,改变加法的运算顺序,它们可以使计算更加简便。 生2:在计算加法时,要先观察数据的特点,运用加法的运算定律把可以凑成整十、整百、几百几十……的数先相加,可以使计算简便。: 鼓励学生自主整理知识,善于自我学习,提升学习力。
环节五 布置作业 教材P23练习六 第1、8、9题
环节六 拓展延伸 同学们,你们听说过数学家高斯小时候计算: 1+2+3+4+5+ …+99+100的和是多少的故事吗? 1+2+3+4+5+ …+99+100=? 微课视频 高斯这样解释: 因为1+100=101,2+99=101,3+98=101,…,49+52=101,50+51=101,而像这样和是101的组合一共有50组,所以很快就可以求出:101×50=5050。 =(1+100)+(2+99)+(3+98)+ +(50+51) =(1+100)×100÷2 =101×50 =5050 观看微课视频 分析方法 对学习有余力的学生进行拓展延伸,一方面开阔视野,另一方面发展数学思维,培养数学关键能力。
