人教版四年级下学期数学 第五单元第4课时 三角形的内角和 教案(表格式)
文档属性
| 名称 | 人教版四年级下学期数学 第五单元第4课时 三角形的内角和 教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 182.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 10:39:08 | ||
图片预览

文档简介
第五单元 三角形
第4课时 三角形的内角和
教学内容分析:
三角形的内角和是三角形的一个重要特征。从教材的安排来看,是在学习了三角形的特性及分类之后,同时三角形的内角和又是学生以后学习多边形的内角和及解决实际问题的基础。在呈现教学内容时,我们要重视知识的形成过程,给学生提供动手操作的学具,留给学生充分进行自主探索和交流的空间,让学生通时量、拼、折等活动,在探索、实验、发现、讨论交流中,推理归纳出三角形的内角和是180°,渗透转化思想,为今后学习图形知识打下基础。
教学目标:
1.通过猜想、实验和操作等活动,探究发现三角形内角之和的规律。
2.利用三角形内角之和的规律解决相关问题。
3.体验探究的过程和方法,感受思维提升的过程,激发求知欲和探索兴趣。
教学重点:
认识三角形的内角和是180°。
教学难点:
通过实验探究得出三角形的内角和是180°。
教学过程:
教学 环节 教师活动 学生活动 设计意图
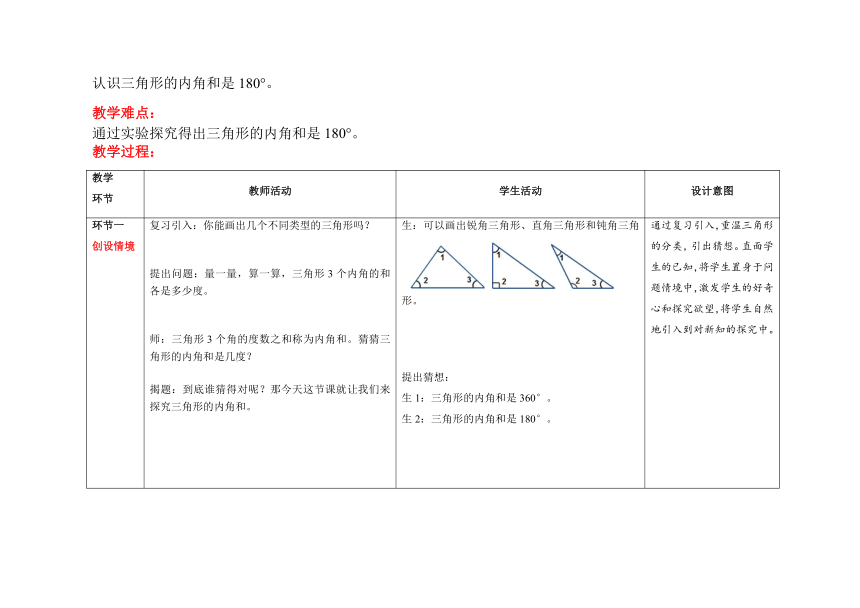
环节一 创设情境 复习引入:你能画出几个不同类型的三角形吗? 提出问题:量一量,算一算,三角形3个内角的和各是多少度。 师:三角形3个角的度数之和称为内角和。猜猜三角形的内角和是几度? 揭题:到底谁猜得对呢?那今天这节课就让我们来探究三角形的内角和。 生:可以画出锐角三角形、直角三角形和钝角三角形。 提出猜想: 生1:三角形的内角和是360°。 生2:三角形的内角和是180°。 通过复习引入,重温三角形的分类,引出猜想。直面学生的已知,将学生置身于问题情境中,激发学生的好奇心和探究欲望,将学生自然地引入到对新知的探究中。
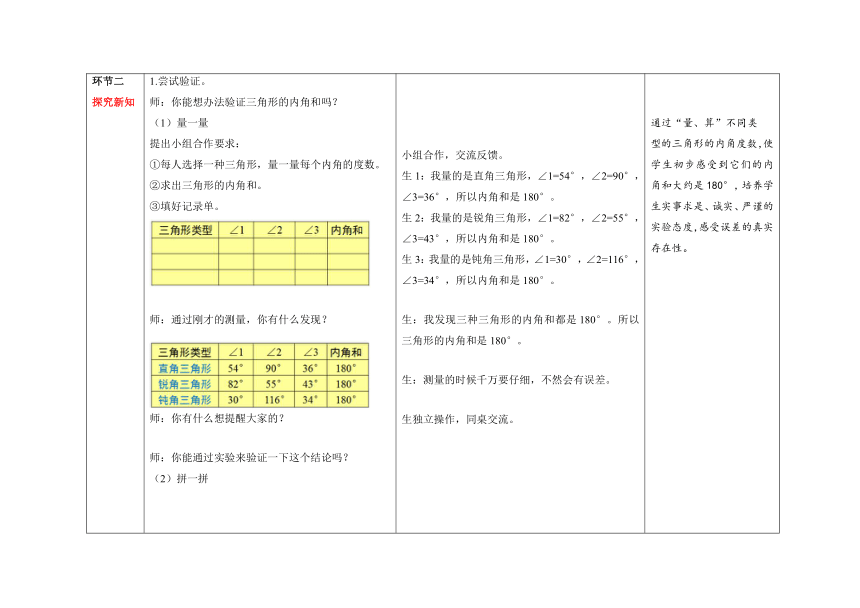
环节二 探究新知 1.尝试验证。 师:你能想办法验证三角形的内角和吗? (1)量一量 提出小组合作要求: ①每人选择一种三角形,量一量每个内角的度数。 ②求出三角形的内角和。 ③填好记录单。 师:通过刚才的测量,你有什么发现? 师:你有什么想提醒大家的? 师:你能通过实验来验证一下这个结论吗? (2)拼一拼 (3)折一折 师:还有别的方法吗? 2.小结。 师:刚才我们是怎么知道三角形内角和是180°的? 小组合作,交流反馈。 生1:我量的是直角三角形,∠1=54°,∠2=90°,∠3=36°,所以内角和是180°。 生2:我量的是锐角三角形,∠1=82°,∠2=55°,∠3=43°,所以内角和是180°。 生3:我量的是钝角三角形,∠1=30°,∠2=116°,∠3=34°,所以内角和是180°。 生:我发现三种三角形的内角和都是180°。所以三角形的内角和是180°。 生:测量的时候千万要仔细,不然会有误差。 生独立操作,同桌交流。 生:我把三角形的三个角先作好标记,撕下来后,发现正好能拼成一个平角。 生:我用了折一折的方法也能验证这个结论,通过折叠后我发现三角形的三个内角放在一起,可以拼成一个平角。 生1:我们通过量一量、拼一拼、折一折都发现三角形内角和是180°。 生2:锐角三角形、直角三角形、钝角三角形的内角和是180°,所以任何三角形的内角和都是180°。 通过“量、算”不同类 型的三角形的内角度数,使学生初步感受到它们的内角和大约是180°,培养学生实事求是、诚实、严谨的实验态度,感受误差的真实存在性。 在量一量得出结论的基础上,构建“拼一拼、折一折”的活动,引导学生用实验的方法验证三角形的内角和是180°,培养学生的严谨思维,体现方法的多样性。
环节三 巩固新知 1.在一个三角形中,∠1=120°,∠3=35°, 求∠2的度数。 2.红领巾的形状是等腰三角形,其中∠1=110°。 ∠1= 110° ∠2=( ) ∠3=( ) 3.把这个三角形平均分成两个小三角形,每个小三角形的内角和是多少度? 师:把两个小三角形拼成一个大三角形,这个大三角形的内角和是多少度? 课件演示,验证结论。 独立解决,交流方法。 生:因为三角形的内角和是180°,∠1=120°,∠3=35°,所以只要用180°减去这两个角的度数就是∠2的度数,所以180°-120°-35°=25°。 独立解决,交流方法。 生:根据三角形的内角是是180°,我们可以求出∠2+∠3=180°-110°=70°,又因为等腰三角形的底角是相等的,所以∠2=∠3=70÷2=35°。 独立思考,交流思路。 生:因为三角形的内角和是180°,所以两个小三角形的内角和也分别是180°。 独立思考,交流思路。 生1:我认为一个三角形的内角和是180°,所以两个小三角形拼在一起是360°。 生2:把两个小三角形拼成一个大三角形,它还是三个内角,所以这个大三角形的内角和还是180°。 第1题是直接应用“三角形的内角和是180°”来计算求解的基础性练习题。 第2题是和日常生活联系比较紧密的题目,借助等腰三角形的性质和三角形内角和,求出底角的度数,既可激发学生的兴趣,又能体会数学的应用价值。 第3题聚焦易错点,让学生灵活运用“三角形内角和等于180°”,将逻辑推理的思想渗透其中,深化对三角形内角和的认识。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 生1:可以通过量一量、拼一拼、折一折等方法验证三角形的内角和是180°。 生2:学会运用三角形的内角和是180°的知识解决生活中的问题。 鼓励学生畅谈自己的收获和体会。
环节五 布置作业 教材练习十六P69第1,2,3题
第4课时 三角形的内角和
教学内容分析:
三角形的内角和是三角形的一个重要特征。从教材的安排来看,是在学习了三角形的特性及分类之后,同时三角形的内角和又是学生以后学习多边形的内角和及解决实际问题的基础。在呈现教学内容时,我们要重视知识的形成过程,给学生提供动手操作的学具,留给学生充分进行自主探索和交流的空间,让学生通时量、拼、折等活动,在探索、实验、发现、讨论交流中,推理归纳出三角形的内角和是180°,渗透转化思想,为今后学习图形知识打下基础。
教学目标:
1.通过猜想、实验和操作等活动,探究发现三角形内角之和的规律。
2.利用三角形内角之和的规律解决相关问题。
3.体验探究的过程和方法,感受思维提升的过程,激发求知欲和探索兴趣。
教学重点:
认识三角形的内角和是180°。
教学难点:
通过实验探究得出三角形的内角和是180°。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 复习引入:你能画出几个不同类型的三角形吗? 提出问题:量一量,算一算,三角形3个内角的和各是多少度。 师:三角形3个角的度数之和称为内角和。猜猜三角形的内角和是几度? 揭题:到底谁猜得对呢?那今天这节课就让我们来探究三角形的内角和。 生:可以画出锐角三角形、直角三角形和钝角三角形。 提出猜想: 生1:三角形的内角和是360°。 生2:三角形的内角和是180°。 通过复习引入,重温三角形的分类,引出猜想。直面学生的已知,将学生置身于问题情境中,激发学生的好奇心和探究欲望,将学生自然地引入到对新知的探究中。
环节二 探究新知 1.尝试验证。 师:你能想办法验证三角形的内角和吗? (1)量一量 提出小组合作要求: ①每人选择一种三角形,量一量每个内角的度数。 ②求出三角形的内角和。 ③填好记录单。 师:通过刚才的测量,你有什么发现? 师:你有什么想提醒大家的? 师:你能通过实验来验证一下这个结论吗? (2)拼一拼 (3)折一折 师:还有别的方法吗? 2.小结。 师:刚才我们是怎么知道三角形内角和是180°的? 小组合作,交流反馈。 生1:我量的是直角三角形,∠1=54°,∠2=90°,∠3=36°,所以内角和是180°。 生2:我量的是锐角三角形,∠1=82°,∠2=55°,∠3=43°,所以内角和是180°。 生3:我量的是钝角三角形,∠1=30°,∠2=116°,∠3=34°,所以内角和是180°。 生:我发现三种三角形的内角和都是180°。所以三角形的内角和是180°。 生:测量的时候千万要仔细,不然会有误差。 生独立操作,同桌交流。 生:我把三角形的三个角先作好标记,撕下来后,发现正好能拼成一个平角。 生:我用了折一折的方法也能验证这个结论,通过折叠后我发现三角形的三个内角放在一起,可以拼成一个平角。 生1:我们通过量一量、拼一拼、折一折都发现三角形内角和是180°。 生2:锐角三角形、直角三角形、钝角三角形的内角和是180°,所以任何三角形的内角和都是180°。 通过“量、算”不同类 型的三角形的内角度数,使学生初步感受到它们的内角和大约是180°,培养学生实事求是、诚实、严谨的实验态度,感受误差的真实存在性。 在量一量得出结论的基础上,构建“拼一拼、折一折”的活动,引导学生用实验的方法验证三角形的内角和是180°,培养学生的严谨思维,体现方法的多样性。
环节三 巩固新知 1.在一个三角形中,∠1=120°,∠3=35°, 求∠2的度数。 2.红领巾的形状是等腰三角形,其中∠1=110°。 ∠1= 110° ∠2=( ) ∠3=( ) 3.把这个三角形平均分成两个小三角形,每个小三角形的内角和是多少度? 师:把两个小三角形拼成一个大三角形,这个大三角形的内角和是多少度? 课件演示,验证结论。 独立解决,交流方法。 生:因为三角形的内角和是180°,∠1=120°,∠3=35°,所以只要用180°减去这两个角的度数就是∠2的度数,所以180°-120°-35°=25°。 独立解决,交流方法。 生:根据三角形的内角是是180°,我们可以求出∠2+∠3=180°-110°=70°,又因为等腰三角形的底角是相等的,所以∠2=∠3=70÷2=35°。 独立思考,交流思路。 生:因为三角形的内角和是180°,所以两个小三角形的内角和也分别是180°。 独立思考,交流思路。 生1:我认为一个三角形的内角和是180°,所以两个小三角形拼在一起是360°。 生2:把两个小三角形拼成一个大三角形,它还是三个内角,所以这个大三角形的内角和还是180°。 第1题是直接应用“三角形的内角和是180°”来计算求解的基础性练习题。 第2题是和日常生活联系比较紧密的题目,借助等腰三角形的性质和三角形内角和,求出底角的度数,既可激发学生的兴趣,又能体会数学的应用价值。 第3题聚焦易错点,让学生灵活运用“三角形内角和等于180°”,将逻辑推理的思想渗透其中,深化对三角形内角和的认识。
环节四 课堂小结 你有什么收获? 回顾本节课自己的体会和收获。 生1:可以通过量一量、拼一拼、折一折等方法验证三角形的内角和是180°。 生2:学会运用三角形的内角和是180°的知识解决生活中的问题。 鼓励学生畅谈自己的收获和体会。
环节五 布置作业 教材练习十六P69第1,2,3题
