人教版五年级下学期数学第三单元 第5课时《长方体和正方体的体积》教案(表格式)
文档属性
| 名称 | 人教版五年级下学期数学第三单元 第5课时《长方体和正方体的体积》教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 333.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 10:51:52 | ||
图片预览


文档简介
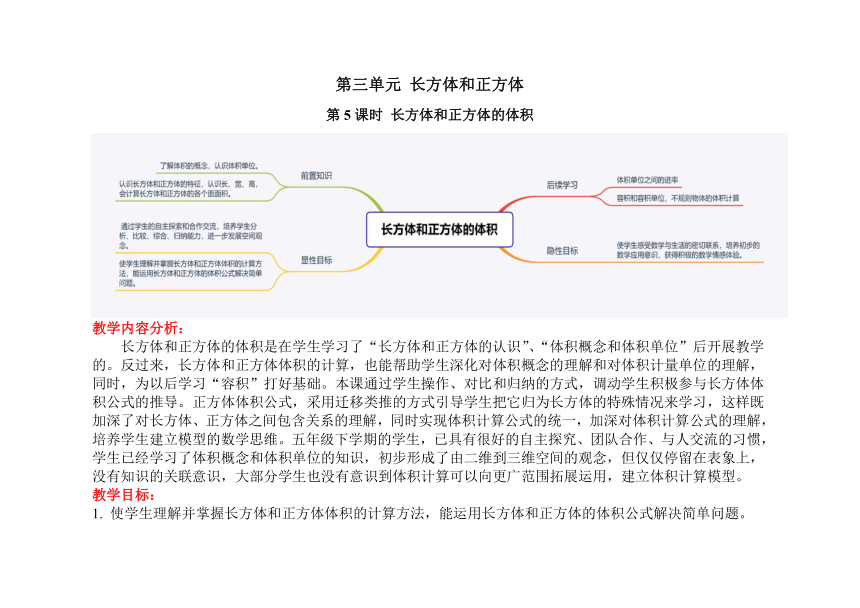
第三单元 长方体和正方体
第5课时 长方体和正方体的体积
教学内容分析:
长方体和正方体的体积是在学生学习了“长方体和正方体的认识”、“体积概念和体积单位”后开展教学的。反过来,长方体和正方体体积的计算,也能帮助学生深化对体积概念的理解和对体积计量单位的理解,同时,为以后学习“容积”打好基础。本课通过学生操作、对比和归纳的方式,调动学生积极参与长方体体积公式的推导。正方体体积公式,采用迁移类推的方式引导学生把它归为长方体的特殊情况来学习,这样既加深了对长方体、正方体之间包含关系的理解,同时实现体积计算公式的统一,加深对体积计算公式的理解,培养学生建立模型的数学思维。五年级下学期的学生,已具有很好的自主探究、团队合作、与人交流的习惯,学生已经学习了体积概念和体积单位的知识,初步形成了由二维到三维空间的观念,但仅仅停留在表象上,没有知识的关联意识,大部分学生也没有意识到体积计算可以向更广范围拓展运用,建立体积计算模型。
教学目标:
1. 使学生理解并掌握长方体和正方体体积的计算方法,能运用长方体和正方体的体积公式解决简单问题。
2. 通过学生的自主探索和合作交流,培养学生分析、比较、综合、归纳能力,进一步发展空间观念。
3. 使学生感受数学与生活的密切联系,培养初步的数学应用意识,获得积极的数学情感体验。
教学重点:
理解并掌握长方体和正方体的体积计算方法。
教学难点:
理解长方体的体积计算公式的推导过程。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 师:已经学过的统一的体积单位有哪些? 师:下图是用棱长1cm的小正方体拼成的,它的体积是多少? 师::数出有多少个体积单位,就知道了它的体积是多少。 师:除了数一数,还有其他方法求长方体的体积吗?探究一下吧! 生:立方厘米、立方分米、立方米。 生:一层有3个正方体,有3层,共9个,是9立方厘米。 通过复习引导学生回顾知识:要计算一个物体的体积,就要看这个物体含有多少个体积单位。通过数一数体积是多少,也为下一步推导长方体的体积公式打下基础。
环节二 探究新知 1. 动手操作,感知公式 师:用体积为1cm 的小正方体摆成不同的长方体,组内交流是怎么摆的,并把相关数据填入下表。 2.交流探究,推导公式 (1)长方体的体积公式 师:观察下面表格,结合刚才的操作,有什么发现? 师:以第一小组搭建的长方体为例,为什么长×宽×高就能知道有多少个小正方体? 小结:长方体的体积=长×宽×高 字母公式:V = a b h (2)正方体的体积公式 师:长方体体积的计算方法适合正方体吗、 小结:a a a也可以写作a ,读作a的立方,表示3个a相乘,所以正方体的体积计算公式一般写成:V = a 。 (3)长方体和正方体统一的体积公式 师:棱长×棱长,长×宽都是先算出了第一层的面积,也就是底面的面积,叫做底面积,因此,长方体和正方体的体积也可以这样计算:底面积×高。 用字母可以表示成:V = S h 回答问题: ①我们小组摆出的长方体,长4cm,宽2cm,高2cm,一共16个小正方体,共16cm 。 ②我们小组摆出的长方体,长4cm,宽4cm,高3cm,一共48个小正方体,共48cm 。 ③我们小组摆出的长方体,长3cm,宽2cm,高3cm,一共是18个小正方体,共18cm 。 生1:长方体所含体积单位的数量就是长方体的体积。 生2:小正方体的数量=长方体的长×宽×高。 生3:也就是长方体的体积=长×宽×高。 生1:长×宽就是知道一层有多少个小正方体。 生2:再乘高,就知道2层一共有多少个小正方体。 生3:所以长×宽×高就能知道有多少个小正方体,即长方体的体积=长×宽×高。 生4:如果用字母V表示长方体的体积,用a,b,h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成:V = a b h。 生1:正方体是特殊的长方体,因此体积计算方法也同样适合于正方体。 生1:正方体的长、宽、高都是一样的。 生2:用a表示它的棱长,那么正方体的体积计算公式就可以写成V=a a a 通过对摆法不同的长方体长、宽、高、小正方体的数量、体积等相关数据的分析,一方面帮助学生进一步理解长方体的体积就是长方体所含体积单位的数量多少。另一方面引导学生找出长方体中所含体积单位的数量与它的长、宽、高的关系,从而总结出长方体体积的计算公式。做到使学生知其然,更知其所以然。进一步体验只要求出了长、宽、高,就能很快算出体积。 正方体是特殊的长方体,因此公式的推导采用迁移类推,学生能更好理解和掌握。 这部分教学将长方体、正方体的体积公式统一为“底面积×高”,让学生理解长方体和正方体的体积公式之间的内在联系,同时,也为今后学习其他柱体体积计算公式作铺垫。
环节三 巩固新知 练习1:计算下面图形的体积。 练习2. 填空。 (1)一个长方体鱼缸,长是4dm,宽是3dm,高是5dm,这个鱼缸的体积是( )dm 。 (2)用棱长2cm的小正方体拼成一个大正方体,这个大正方体的体积至少是( )cm 。 练习3. 解决问题。 爸爸制作一个棱长是2dm的正方体无盖玻璃鱼缸,这个鱼缸需要多少平方分米的玻璃?这个鱼缸的体积是多少立方分米? V = a b h =7×3×4 =21×4 =84(cm ) V = a =5 =5×5×5 =125(cm ) V = S h =12×6 =72(cm ) 60 64 S= 2×2×5 =20(dm ) V= a =2×2×2 =8(dm ) 答:这个鱼缸需要20平方分米的玻璃,这个鱼缸的体积是8立方分米。 练习1的目的是巩固长方体和正方体体积的计算方法,同时,第三幅图的底面位置发生变化,巩固底面积×高的同时,也凸显底面和高的位置关系。 练习2的目的进一步提升学生空间想象能力,练习从直观图到文字表达,学生需要建立空间的想象模型,提升了练习的思维含量。 练习3的目的是与生活实际联系,感受数学的工具性,同时,与表面积相结合,能够让学生对比巩固概念。
环节四 课堂小结 你有什么收获? ①通过操作与交流理解了公式的推导过程。 ②掌握了长方体和正方体体积的计算方法: 长方体的体积公式:V = a b h 正方体的体积公式:V = a ②在解决实际问题中,能区分表面积和体积,能运用长方体和正方体的体积公式解决简单问题。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 布置作业 教材P32、33 练习七 第7、8、9题
第5课时 长方体和正方体的体积
教学内容分析:
长方体和正方体的体积是在学生学习了“长方体和正方体的认识”、“体积概念和体积单位”后开展教学的。反过来,长方体和正方体体积的计算,也能帮助学生深化对体积概念的理解和对体积计量单位的理解,同时,为以后学习“容积”打好基础。本课通过学生操作、对比和归纳的方式,调动学生积极参与长方体体积公式的推导。正方体体积公式,采用迁移类推的方式引导学生把它归为长方体的特殊情况来学习,这样既加深了对长方体、正方体之间包含关系的理解,同时实现体积计算公式的统一,加深对体积计算公式的理解,培养学生建立模型的数学思维。五年级下学期的学生,已具有很好的自主探究、团队合作、与人交流的习惯,学生已经学习了体积概念和体积单位的知识,初步形成了由二维到三维空间的观念,但仅仅停留在表象上,没有知识的关联意识,大部分学生也没有意识到体积计算可以向更广范围拓展运用,建立体积计算模型。
教学目标:
1. 使学生理解并掌握长方体和正方体体积的计算方法,能运用长方体和正方体的体积公式解决简单问题。
2. 通过学生的自主探索和合作交流,培养学生分析、比较、综合、归纳能力,进一步发展空间观念。
3. 使学生感受数学与生活的密切联系,培养初步的数学应用意识,获得积极的数学情感体验。
教学重点:
理解并掌握长方体和正方体的体积计算方法。
教学难点:
理解长方体的体积计算公式的推导过程。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 师:已经学过的统一的体积单位有哪些? 师:下图是用棱长1cm的小正方体拼成的,它的体积是多少? 师::数出有多少个体积单位,就知道了它的体积是多少。 师:除了数一数,还有其他方法求长方体的体积吗?探究一下吧! 生:立方厘米、立方分米、立方米。 生:一层有3个正方体,有3层,共9个,是9立方厘米。 通过复习引导学生回顾知识:要计算一个物体的体积,就要看这个物体含有多少个体积单位。通过数一数体积是多少,也为下一步推导长方体的体积公式打下基础。
环节二 探究新知 1. 动手操作,感知公式 师:用体积为1cm 的小正方体摆成不同的长方体,组内交流是怎么摆的,并把相关数据填入下表。 2.交流探究,推导公式 (1)长方体的体积公式 师:观察下面表格,结合刚才的操作,有什么发现? 师:以第一小组搭建的长方体为例,为什么长×宽×高就能知道有多少个小正方体? 小结:长方体的体积=长×宽×高 字母公式:V = a b h (2)正方体的体积公式 师:长方体体积的计算方法适合正方体吗、 小结:a a a也可以写作a ,读作a的立方,表示3个a相乘,所以正方体的体积计算公式一般写成:V = a 。 (3)长方体和正方体统一的体积公式 师:棱长×棱长,长×宽都是先算出了第一层的面积,也就是底面的面积,叫做底面积,因此,长方体和正方体的体积也可以这样计算:底面积×高。 用字母可以表示成:V = S h 回答问题: ①我们小组摆出的长方体,长4cm,宽2cm,高2cm,一共16个小正方体,共16cm 。 ②我们小组摆出的长方体,长4cm,宽4cm,高3cm,一共48个小正方体,共48cm 。 ③我们小组摆出的长方体,长3cm,宽2cm,高3cm,一共是18个小正方体,共18cm 。 生1:长方体所含体积单位的数量就是长方体的体积。 生2:小正方体的数量=长方体的长×宽×高。 生3:也就是长方体的体积=长×宽×高。 生1:长×宽就是知道一层有多少个小正方体。 生2:再乘高,就知道2层一共有多少个小正方体。 生3:所以长×宽×高就能知道有多少个小正方体,即长方体的体积=长×宽×高。 生4:如果用字母V表示长方体的体积,用a,b,h分别表示长方体的长、宽、高,那么长方体的体积计算公式可以写成:V = a b h。 生1:正方体是特殊的长方体,因此体积计算方法也同样适合于正方体。 生1:正方体的长、宽、高都是一样的。 生2:用a表示它的棱长,那么正方体的体积计算公式就可以写成V=a a a 通过对摆法不同的长方体长、宽、高、小正方体的数量、体积等相关数据的分析,一方面帮助学生进一步理解长方体的体积就是长方体所含体积单位的数量多少。另一方面引导学生找出长方体中所含体积单位的数量与它的长、宽、高的关系,从而总结出长方体体积的计算公式。做到使学生知其然,更知其所以然。进一步体验只要求出了长、宽、高,就能很快算出体积。 正方体是特殊的长方体,因此公式的推导采用迁移类推,学生能更好理解和掌握。 这部分教学将长方体、正方体的体积公式统一为“底面积×高”,让学生理解长方体和正方体的体积公式之间的内在联系,同时,也为今后学习其他柱体体积计算公式作铺垫。
环节三 巩固新知 练习1:计算下面图形的体积。 练习2. 填空。 (1)一个长方体鱼缸,长是4dm,宽是3dm,高是5dm,这个鱼缸的体积是( )dm 。 (2)用棱长2cm的小正方体拼成一个大正方体,这个大正方体的体积至少是( )cm 。 练习3. 解决问题。 爸爸制作一个棱长是2dm的正方体无盖玻璃鱼缸,这个鱼缸需要多少平方分米的玻璃?这个鱼缸的体积是多少立方分米? V = a b h =7×3×4 =21×4 =84(cm ) V = a =5 =5×5×5 =125(cm ) V = S h =12×6 =72(cm ) 60 64 S= 2×2×5 =20(dm ) V= a =2×2×2 =8(dm ) 答:这个鱼缸需要20平方分米的玻璃,这个鱼缸的体积是8立方分米。 练习1的目的是巩固长方体和正方体体积的计算方法,同时,第三幅图的底面位置发生变化,巩固底面积×高的同时,也凸显底面和高的位置关系。 练习2的目的进一步提升学生空间想象能力,练习从直观图到文字表达,学生需要建立空间的想象模型,提升了练习的思维含量。 练习3的目的是与生活实际联系,感受数学的工具性,同时,与表面积相结合,能够让学生对比巩固概念。
环节四 课堂小结 你有什么收获? ①通过操作与交流理解了公式的推导过程。 ②掌握了长方体和正方体体积的计算方法: 长方体的体积公式:V = a b h 正方体的体积公式:V = a ②在解决实际问题中,能区分表面积和体积,能运用长方体和正方体的体积公式解决简单问题。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 布置作业 教材P32、33 练习七 第7、8、9题
