五年级下学期数学第三单元第3课时《长方体和正方体的表面积》(教案表格式)
文档属性
| 名称 | 五年级下学期数学第三单元第3课时《长方体和正方体的表面积》(教案表格式) | 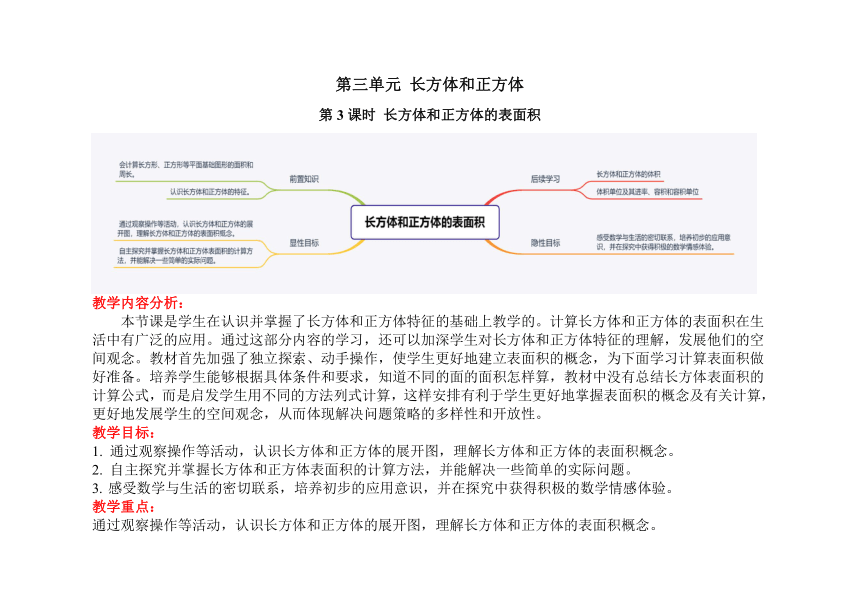 | |
| 格式 | docx | ||
| 文件大小 | 281.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 10:52:22 | ||
图片预览

文档简介
第三单元 长方体和正方体
第3课时 长方体和正方体的表面积
教学内容分析:
本节课是学生在认识并掌握了长方体和正方体特征的基础上教学的。计算长方体和正方体的表面积在生活中有广泛的应用。通过这部分内容的学习,还可以加深学生对长方体和正方体特征的理解,发展他们的空间观念。教材首先加强了独立探索、动手操作,使学生更好地建立表面积的概念,为下面学习计算表面积做好准备。培养学生能够根据具体条件和要求,知道不同的面的面积怎样算,教材中没有总结长方体表面积的计算公式,而是启发学生用不同的方法列式计算,这样安排有利于学生更好地掌握表面积的概念及有关计算,更好地发展学生的空间观念,从而体现解决问题策略的多样性和开放性。
教学目标:
1. 通过观察操作等活动,认识长方体和正方体的展开图,理解长方体和正方体的表面积概念。
2. 自主探究并掌握长方体和正方体表面积的计算方法,并能解决一些简单的实际问题。
3. 感受数学与生活的密切联系,培养初步的应用意识,并在探究中获得积极的数学情感体验。
教学重点:
通过观察操作等活动,认识长方体和正方体的展开图,理解长方体和正方体的表面积概念。
教学难点:
自主探究并掌握长方体和正方体表面积的计算方法,并能解决一些简单的实际问题。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 师:同学们,我们一起来复习关于长方体和正方体的知识吧。 1.长方体一般是由6个( )(特殊情况有两个相对的面是正方形 )围成的立体图形。 2.在一个长方体中,相对的面( ),相对的棱( )。 3.正方体是由6个( )围成的立体图形。 4.下图是一个( ),它的棱长是( )厘米,它的棱长之和是( )厘米。 生1:长方形 生2:完全相同 长度相等 生3:正方形 生4:正方体 6 72 通过复习长方体和正方体的相关知识,为学生创设了想象空间,发展思维,为学生学习新知做了铺垫,使学生顺利进入下一环节的学习。
环节二 探究新知 一.想象图形,初尝概念 师:把右边长方体沿着棱剪开,展开后不可能出现哪种图形? 师:1号是不是长方体的展开图,我们可以通过剪一剪或折一折进行验证。 师:2号是不是长方体的展开图,请你想象下,看能否找出相对应的面。 师:观察下面的展开图是不是正方形。 请同学们在草稿纸上画一个这样的展开图,折一折,能不能围成正方形 课外拓展:一共有11种正方体展开图。(动态图展示) 师:观看11种正方体的展开图。 2.出示概念,自主探究 师:长方体或正方体6个面的总面积,叫做它的表面积。 做一个微波炉的包装箱,至少要用多少平方米的硬纸板? 师:大家尝试计算。 师:在计算长方体表面积时,我们的解题思路是怎样的? 师:长方体表面积=(长+宽+高)×2 师:谁再来试一试。 3.探究方法,解决问题 一个正方体墨水盒棱长为6.5cm,制作这个墨水盒至少需要多少平方厘米的硬纸板。 师:说一说你的计算思路。 师:正方体表面积=棱长×棱长×6 师:请同学们尝试计算。 生:不可能是3号,因为3号只有5个面,长方体展开图应该有6个面。 生:1号是长方体的展开图,而且上下面、前后面、左右面都是相隔的。 生1:我认为2号也是,而且我分别找出了相对应的面。 生2:我发现,右面的长就是上面的宽,右面的宽是前面的宽,3个面正好连接。 生:可以。 生:我先求上下每个面:长是0.7m,宽是0.5m,面积是0.35,前后每个面:长是0.7m,宽是0.4m,面积是0.28,左右每个面:长是0.5m,宽是0.4m,面积是0.2,最后相加表面积一共是1.66平方米。 生1:就是要求这个长方体纸盒的表面积。 生2:我先求上下两个面的面积,再求前后两个面的面积,最后求左右两个面的面积 生3:因为相对面是完全相同的,因此也可以求上面+前面+左面,最后再乘以2就可以了。 生:(0.7×0.5+0.7×0.4+0.5×0.4)×2=1.66(平方米) 答:至少要用1.66平方米的硬纸板。 生:正方体每个面都完全相同,所以只要求出一个面乘以6就可以得到表面积了。 生:6.5×6.5×6=253.5(平方厘米) 答:制作这个墨水盒至少需要253.5平方厘米的硬纸板。 在想象展开图的活动中,充分创设空间,发展学生思维,同时,通过排除不可能出现的图形这一活动,又一次巩固了长方体6个面的概念,为新知教学铺垫。 通过剪一剪或折一折的活动进行验证操作,使学生感受从观察到想象,从假设到验证的数学思考方法,并且在验证中发现相对面都是相隔的。 强化学生的空间想象,通过从展开图到实物图的逆向思考,找到相对应的面,是对学生思维的一种提升考验,同时,通过观察、交流,发现长、宽、高是把3个面连接起来的重要因素。 动静结合,出示正方体展开图的11种可能图,拓展课外知识。 学生自主探究,老师再引导总结,梳理计算长方体表面积的方法,不出示计算公式,更能激发学生主动学习的兴趣。 在交流中,基于长方体表面积计算方法的探究,梳理出正方体表面积计算方法。
环节三 巩固新知 练习1:在下面的图形中,不是正方体的平面展开图的是( )。 A.B.C.D. 练习2:亮亮家要给一个长0.75米,宽0.5米,高1.6米的简易衣柜换布罩(如右图,没有底面)。至少需要用布多少平方米。 练习3:用3个长为5厘米,宽为2.5厘米,高为1厘米的长方体拼成一个较大的长方体(如图)这个长方体的表面积是多少? 生:C 生: 前后面:0.75×1.6×2=2.4(平方米) 左右面:0.5×1.6×2=1.6(平方米) 上面:0.5×0.75=0.375(平方米) 一共:2.4+1.6+0.375=4.375(平方米) 答:至少需要用布4.375平方米。 方法一: 上下面:5×2.5×2=25(平方厘米) 左右面:2.5×3×2=15(平方厘米) 前后面:5×3×2=30(平方厘米) 一共:25+15+30=70(平方厘米) 方法二: 原1个(5×2.5+5×1+1×2.5)×2 =20×2 =40(平方厘米) 少的面:5×2.5×4=50(平方厘米) 一共:40×3-50=70(平方厘米) 答:这个长方体的表面积是70平方厘米。 练习1的目的是进一步理清长方体表面积计算方法,同时与现实生活相联系,体会数学解决问题的灵活性和多样性。 练习2的目的进一步提升学生空间想象能力,培养数学推理能力,同时加强数学语言表达的能力。而且通过不同方法的学习,让学生数学解决问题的多样化,灵活数学思维。
环节四 课堂小结 你有什么收获? 生: 认识了长方体和正方体的展开图,理解长方体和正方体的表面积概念。 会解决实际生活中长方体和正方体表面积相关的问题,灵活运用公式。 长方体表面积=(长+宽+高)×2 正方体表面积=棱长×棱长×6 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 布置作业 教材P25 练习六 第1、2、4题。
第3课时 长方体和正方体的表面积
教学内容分析:
本节课是学生在认识并掌握了长方体和正方体特征的基础上教学的。计算长方体和正方体的表面积在生活中有广泛的应用。通过这部分内容的学习,还可以加深学生对长方体和正方体特征的理解,发展他们的空间观念。教材首先加强了独立探索、动手操作,使学生更好地建立表面积的概念,为下面学习计算表面积做好准备。培养学生能够根据具体条件和要求,知道不同的面的面积怎样算,教材中没有总结长方体表面积的计算公式,而是启发学生用不同的方法列式计算,这样安排有利于学生更好地掌握表面积的概念及有关计算,更好地发展学生的空间观念,从而体现解决问题策略的多样性和开放性。
教学目标:
1. 通过观察操作等活动,认识长方体和正方体的展开图,理解长方体和正方体的表面积概念。
2. 自主探究并掌握长方体和正方体表面积的计算方法,并能解决一些简单的实际问题。
3. 感受数学与生活的密切联系,培养初步的应用意识,并在探究中获得积极的数学情感体验。
教学重点:
通过观察操作等活动,认识长方体和正方体的展开图,理解长方体和正方体的表面积概念。
教学难点:
自主探究并掌握长方体和正方体表面积的计算方法,并能解决一些简单的实际问题。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 创设情境 师:同学们,我们一起来复习关于长方体和正方体的知识吧。 1.长方体一般是由6个( )(特殊情况有两个相对的面是正方形 )围成的立体图形。 2.在一个长方体中,相对的面( ),相对的棱( )。 3.正方体是由6个( )围成的立体图形。 4.下图是一个( ),它的棱长是( )厘米,它的棱长之和是( )厘米。 生1:长方形 生2:完全相同 长度相等 生3:正方形 生4:正方体 6 72 通过复习长方体和正方体的相关知识,为学生创设了想象空间,发展思维,为学生学习新知做了铺垫,使学生顺利进入下一环节的学习。
环节二 探究新知 一.想象图形,初尝概念 师:把右边长方体沿着棱剪开,展开后不可能出现哪种图形? 师:1号是不是长方体的展开图,我们可以通过剪一剪或折一折进行验证。 师:2号是不是长方体的展开图,请你想象下,看能否找出相对应的面。 师:观察下面的展开图是不是正方形。 请同学们在草稿纸上画一个这样的展开图,折一折,能不能围成正方形 课外拓展:一共有11种正方体展开图。(动态图展示) 师:观看11种正方体的展开图。 2.出示概念,自主探究 师:长方体或正方体6个面的总面积,叫做它的表面积。 做一个微波炉的包装箱,至少要用多少平方米的硬纸板? 师:大家尝试计算。 师:在计算长方体表面积时,我们的解题思路是怎样的? 师:长方体表面积=(长+宽+高)×2 师:谁再来试一试。 3.探究方法,解决问题 一个正方体墨水盒棱长为6.5cm,制作这个墨水盒至少需要多少平方厘米的硬纸板。 师:说一说你的计算思路。 师:正方体表面积=棱长×棱长×6 师:请同学们尝试计算。 生:不可能是3号,因为3号只有5个面,长方体展开图应该有6个面。 生:1号是长方体的展开图,而且上下面、前后面、左右面都是相隔的。 生1:我认为2号也是,而且我分别找出了相对应的面。 生2:我发现,右面的长就是上面的宽,右面的宽是前面的宽,3个面正好连接。 生:可以。 生:我先求上下每个面:长是0.7m,宽是0.5m,面积是0.35,前后每个面:长是0.7m,宽是0.4m,面积是0.28,左右每个面:长是0.5m,宽是0.4m,面积是0.2,最后相加表面积一共是1.66平方米。 生1:就是要求这个长方体纸盒的表面积。 生2:我先求上下两个面的面积,再求前后两个面的面积,最后求左右两个面的面积 生3:因为相对面是完全相同的,因此也可以求上面+前面+左面,最后再乘以2就可以了。 生:(0.7×0.5+0.7×0.4+0.5×0.4)×2=1.66(平方米) 答:至少要用1.66平方米的硬纸板。 生:正方体每个面都完全相同,所以只要求出一个面乘以6就可以得到表面积了。 生:6.5×6.5×6=253.5(平方厘米) 答:制作这个墨水盒至少需要253.5平方厘米的硬纸板。 在想象展开图的活动中,充分创设空间,发展学生思维,同时,通过排除不可能出现的图形这一活动,又一次巩固了长方体6个面的概念,为新知教学铺垫。 通过剪一剪或折一折的活动进行验证操作,使学生感受从观察到想象,从假设到验证的数学思考方法,并且在验证中发现相对面都是相隔的。 强化学生的空间想象,通过从展开图到实物图的逆向思考,找到相对应的面,是对学生思维的一种提升考验,同时,通过观察、交流,发现长、宽、高是把3个面连接起来的重要因素。 动静结合,出示正方体展开图的11种可能图,拓展课外知识。 学生自主探究,老师再引导总结,梳理计算长方体表面积的方法,不出示计算公式,更能激发学生主动学习的兴趣。 在交流中,基于长方体表面积计算方法的探究,梳理出正方体表面积计算方法。
环节三 巩固新知 练习1:在下面的图形中,不是正方体的平面展开图的是( )。 A.B.C.D. 练习2:亮亮家要给一个长0.75米,宽0.5米,高1.6米的简易衣柜换布罩(如右图,没有底面)。至少需要用布多少平方米。 练习3:用3个长为5厘米,宽为2.5厘米,高为1厘米的长方体拼成一个较大的长方体(如图)这个长方体的表面积是多少? 生:C 生: 前后面:0.75×1.6×2=2.4(平方米) 左右面:0.5×1.6×2=1.6(平方米) 上面:0.5×0.75=0.375(平方米) 一共:2.4+1.6+0.375=4.375(平方米) 答:至少需要用布4.375平方米。 方法一: 上下面:5×2.5×2=25(平方厘米) 左右面:2.5×3×2=15(平方厘米) 前后面:5×3×2=30(平方厘米) 一共:25+15+30=70(平方厘米) 方法二: 原1个(5×2.5+5×1+1×2.5)×2 =20×2 =40(平方厘米) 少的面:5×2.5×4=50(平方厘米) 一共:40×3-50=70(平方厘米) 答:这个长方体的表面积是70平方厘米。 练习1的目的是进一步理清长方体表面积计算方法,同时与现实生活相联系,体会数学解决问题的灵活性和多样性。 练习2的目的进一步提升学生空间想象能力,培养数学推理能力,同时加强数学语言表达的能力。而且通过不同方法的学习,让学生数学解决问题的多样化,灵活数学思维。
环节四 课堂小结 你有什么收获? 生: 认识了长方体和正方体的展开图,理解长方体和正方体的表面积概念。 会解决实际生活中长方体和正方体表面积相关的问题,灵活运用公式。 长方体表面积=(长+宽+高)×2 正方体表面积=棱长×棱长×6 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 布置作业 教材P25 练习六 第1、2、4题。
