人教版五年级下学期数学第二单元 第7课时《单元综合复习》教案(表格式)
文档属性
| 名称 | 人教版五年级下学期数学第二单元 第7课时《单元综合复习》教案(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 198.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 11:02:10 | ||
图片预览



文档简介
第二单元 因数和倍数
第7课时 单元综合复习
教学内容分析:
本单元一共包括了因数和倍数,2、5、3的倍数的特征,质数和合数,奇偶性等几个方面的内容。作为一节复习课既要考虑到知识点的覆盖是否全面,又要体现出复习课的特点,要通过复习让学生明晰数学知识的要点和脉络,在头脑中构建合理的知识体系。因此,复习时可以先呈现本单元学习了哪些知识,构建一个整体的知识导图。接着围绕着因数和倍数展开,然后通过综合练习和提升练习让学生对所学知识有个整体的回顾与复习。
教学目标:
1. 通过复习与整理,使学生进一步理解倍数、因数、质数、合数、奇数、偶数的概念,明确概念之间的联系和区别。
2. 在复习过程中,引导学生梳理知识建立知识网络,掌握一定的学习方法。
3. 渗透有序思考的数学思想,培养学生发现数学本质规律的意识与能力,提高归纳、概括能力。
4. 使学生体会到生活中处处有数学,增强学好数学的信心和应用数学的意识。
教学重点:
渗透有序思考的数学思想,引导学生发现数学本质规律。
教学难点:
引导学生建立系统化、条理化的知识网络,掌握一定的学习方法。
教学过程:
教学 环节 教师活动 学生活动 设计意图
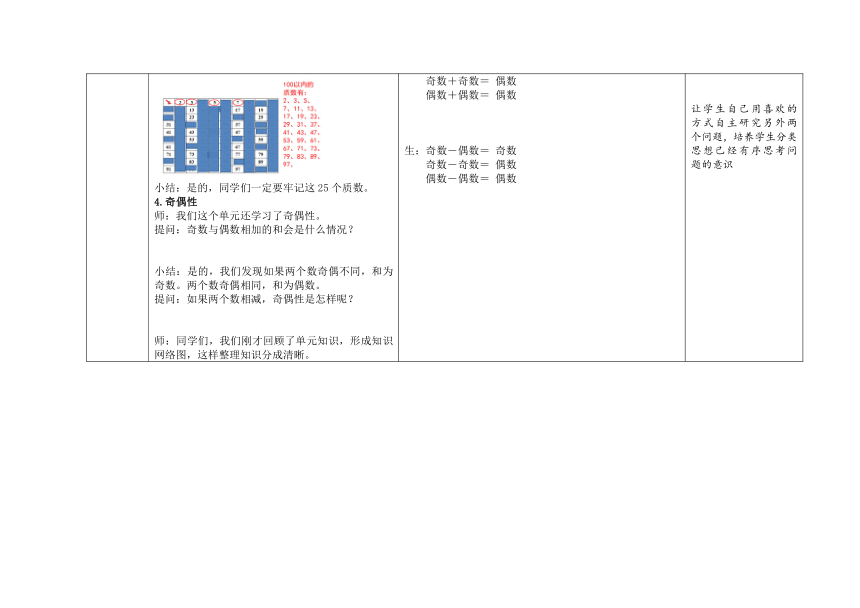
环节一 知识梳理 谈话:同学们,我们先来梳理本单元的知识,构建知识网络。 课件出示本单元教材内容,引领学生整体回顾。 1.复习因数和倍数 提问:什么是因数和倍数? 以12÷2=6为例。 小结:是的,在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数。 师:有什么特别要注意吗? 提问:一个数的因数、倍数有什么特征? 师:为什么没有最大的倍数? 2. 2、5、3的倍数的特征 师:2的倍数有什么特征? 小结:我们可以根据是不是2的倍数把自然数分成奇数和偶数两大类。 课件演示集合图。 提问:5的倍数有什么特征? 提问:3的倍数有什么特征? 3.质数、合数 师:什么是质数?合数? 小结:是的。所以我们可以按因数的个数给自然数分三类。 提问:还记得我们是怎么找到100以内的质数吗? 小结:是的,同学们一定要牢记这25个质数。 4.奇偶性 师:我们这个单元还学习了奇偶性。 提问:奇数与偶数相加的和会是什么情况? 小结:是的,我们发现如果两个数奇偶不同,和为奇数。两个数奇偶相同,和为偶数。 提问:如果两个数相减,奇偶性是怎样呢? 师:同学们,我们刚才回顾了单元知识,形成知识网络图,这样整理知识分成清晰。 学生回顾,本单元的知识。 生:12是2和6的倍数,2和6是12的因数。 生:因数和倍数是相互依存的。 研究因数和倍数的时候我们所说的数指的是非0自然数。 生1:一个数的最小因数是1,最大因数是它本身,个数是有限的。 生2:一个数的最小倍数是它本身,没有最大倍数,个数是无限的。 生:自然数是无限的,所以倍数也是无限的。 生:个位上是0、2、4、6、8的数都是2的倍数。 生:整数中,是2的倍数的数叫做偶数(0也是偶数),不是2的倍数的数叫做奇(jī)数。 生1:个位上是0、5的数都是5的倍数。 生2:个位上是0的数,既是2的倍数也是5的倍数。 生:一个数各位上的数的和是3的倍数,这个数就是3的倍数。 生1:一个数,如果只有1和它本身两个因数,那么这样的数叫做质数(或素数)。 一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。 生:用了排除法。 生:奇数+偶数= 奇数 奇数+奇数= 偶数 偶数+偶数= 偶数 生:奇数-偶数= 奇数 奇数-奇数= 偶数 偶数-偶数= 偶数 开门见山地提出本节课的研究任务,目标明确为后续学习节约时间。 引导学生一起回忆本单元的一些知识点,弄清知识的来龙去脉,沟通其纵横联系,使之条理化、系统化,帮助学生建立良好的认知结构。 复习时,引导学生回顾知识形成的过程,知道有序列举可以发现数学规律的本质。 让学生自己用喜欢的方式自主研究另外两个问题,培养学生分类思想已经有序思考问题的意识
环节二 综合练习 1.填一填: (1)20的因数中最小的是( ),最大的是( )。 (2)1-100这100个自然数中15的倍数有 ( )。 (3)一个是既是65的因数,又是65 的倍数,这个数是( )。 2.判一判: (1)所有的偶数都是合数。( ) (2)所有的奇数都是质数。( ) (3)7的倍数都是合数。( ) (4)两个质数的和是偶数。( ) 3.猜一猜: 生:1,20 生:15,30,45,60,75,90 生:65 生: (1)错,2是偶数但不是合数。 (2)错,9是奇数但不是质数。 (3)错,7的1倍是7,是质数。 (4)错,不要以为质数都是奇数,而奇数+奇数=偶数,要考虑2,2+3=5,结果是一个奇数。 生1:3、7。 生2:7、13。 生3:2、4 通过多种不同形式的练习,培养学生运用所学知识解决问题的能力,体现数学的应用价值。
环节三 拓展练习 二、提升练习 1.算一算: (1)奇数与奇数的积是奇数还是偶数 (2)奇数与偶数的积是奇数还是偶数 (3)偶数与偶数的积呢 提问:可以怎么研究? 2.找一找: 小虎在侦破一个案件时发现了一个保险箱。保险箱设有六位数的密码。已知: A是5最大的因数; B的所有因数是1,2,4,8; C是最小的自然数; D只有一个因数; E既是质数又是偶数; F既是9的因数又是9的倍数。 3.试一试: 老师报出一个大于2的偶数,你能找出和为此数的两个质数吗? 例:4=2+2,8=3+5 提问:你能试试看下面这几个数吗? 10, 12, 14, 16, 18, 20 师:介绍哥德巴赫猜想。是不是所有大于2的偶数,都可以表示为两个质数的和呢? 生:举例子探究。 生:奇数×奇数 = 奇数 奇数×偶数 = 偶数 偶数×偶数 = 偶数 生:A是5,因为5的最大因数是它本身; B是8,8有四个因数,它的最大因数也是8; C是0,0是最小的自然数; D是1,1的因数只有1; E是2,偶数中只有2是质数; F是9,一个数是它自己的最大因数,又是自己的最小倍数。所以密码是580129。 生:10=3+7=5+5,12=5+7 14=3+11=7+7 16=3+13=5+11, 18=5+13=7+11, 20=3+17=7+13 选取3道探究的题型,鼓励学生自主探究,积极思考,养成勇于探究乐于思考的精神。
环节四 课堂小结 你有什么收获? 生1:复习了因数、倍数、质数、合数有关的知识。 生2:理清了知识点之间的联系。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 布置作业 教材P16 练习四第5题
第7课时 单元综合复习
教学内容分析:
本单元一共包括了因数和倍数,2、5、3的倍数的特征,质数和合数,奇偶性等几个方面的内容。作为一节复习课既要考虑到知识点的覆盖是否全面,又要体现出复习课的特点,要通过复习让学生明晰数学知识的要点和脉络,在头脑中构建合理的知识体系。因此,复习时可以先呈现本单元学习了哪些知识,构建一个整体的知识导图。接着围绕着因数和倍数展开,然后通过综合练习和提升练习让学生对所学知识有个整体的回顾与复习。
教学目标:
1. 通过复习与整理,使学生进一步理解倍数、因数、质数、合数、奇数、偶数的概念,明确概念之间的联系和区别。
2. 在复习过程中,引导学生梳理知识建立知识网络,掌握一定的学习方法。
3. 渗透有序思考的数学思想,培养学生发现数学本质规律的意识与能力,提高归纳、概括能力。
4. 使学生体会到生活中处处有数学,增强学好数学的信心和应用数学的意识。
教学重点:
渗透有序思考的数学思想,引导学生发现数学本质规律。
教学难点:
引导学生建立系统化、条理化的知识网络,掌握一定的学习方法。
教学过程:
教学 环节 教师活动 学生活动 设计意图
环节一 知识梳理 谈话:同学们,我们先来梳理本单元的知识,构建知识网络。 课件出示本单元教材内容,引领学生整体回顾。 1.复习因数和倍数 提问:什么是因数和倍数? 以12÷2=6为例。 小结:是的,在整数除法中,如果商是整数而没有余数,我们就说被除数是除数和商的倍数,除数和商是被除数的因数。 师:有什么特别要注意吗? 提问:一个数的因数、倍数有什么特征? 师:为什么没有最大的倍数? 2. 2、5、3的倍数的特征 师:2的倍数有什么特征? 小结:我们可以根据是不是2的倍数把自然数分成奇数和偶数两大类。 课件演示集合图。 提问:5的倍数有什么特征? 提问:3的倍数有什么特征? 3.质数、合数 师:什么是质数?合数? 小结:是的。所以我们可以按因数的个数给自然数分三类。 提问:还记得我们是怎么找到100以内的质数吗? 小结:是的,同学们一定要牢记这25个质数。 4.奇偶性 师:我们这个单元还学习了奇偶性。 提问:奇数与偶数相加的和会是什么情况? 小结:是的,我们发现如果两个数奇偶不同,和为奇数。两个数奇偶相同,和为偶数。 提问:如果两个数相减,奇偶性是怎样呢? 师:同学们,我们刚才回顾了单元知识,形成知识网络图,这样整理知识分成清晰。 学生回顾,本单元的知识。 生:12是2和6的倍数,2和6是12的因数。 生:因数和倍数是相互依存的。 研究因数和倍数的时候我们所说的数指的是非0自然数。 生1:一个数的最小因数是1,最大因数是它本身,个数是有限的。 生2:一个数的最小倍数是它本身,没有最大倍数,个数是无限的。 生:自然数是无限的,所以倍数也是无限的。 生:个位上是0、2、4、6、8的数都是2的倍数。 生:整数中,是2的倍数的数叫做偶数(0也是偶数),不是2的倍数的数叫做奇(jī)数。 生1:个位上是0、5的数都是5的倍数。 生2:个位上是0的数,既是2的倍数也是5的倍数。 生:一个数各位上的数的和是3的倍数,这个数就是3的倍数。 生1:一个数,如果只有1和它本身两个因数,那么这样的数叫做质数(或素数)。 一个数,如果除了1和它本身还有别的因数,那么这样的数叫做合数。 生:用了排除法。 生:奇数+偶数= 奇数 奇数+奇数= 偶数 偶数+偶数= 偶数 生:奇数-偶数= 奇数 奇数-奇数= 偶数 偶数-偶数= 偶数 开门见山地提出本节课的研究任务,目标明确为后续学习节约时间。 引导学生一起回忆本单元的一些知识点,弄清知识的来龙去脉,沟通其纵横联系,使之条理化、系统化,帮助学生建立良好的认知结构。 复习时,引导学生回顾知识形成的过程,知道有序列举可以发现数学规律的本质。 让学生自己用喜欢的方式自主研究另外两个问题,培养学生分类思想已经有序思考问题的意识
环节二 综合练习 1.填一填: (1)20的因数中最小的是( ),最大的是( )。 (2)1-100这100个自然数中15的倍数有 ( )。 (3)一个是既是65的因数,又是65 的倍数,这个数是( )。 2.判一判: (1)所有的偶数都是合数。( ) (2)所有的奇数都是质数。( ) (3)7的倍数都是合数。( ) (4)两个质数的和是偶数。( ) 3.猜一猜: 生:1,20 生:15,30,45,60,75,90 生:65 生: (1)错,2是偶数但不是合数。 (2)错,9是奇数但不是质数。 (3)错,7的1倍是7,是质数。 (4)错,不要以为质数都是奇数,而奇数+奇数=偶数,要考虑2,2+3=5,结果是一个奇数。 生1:3、7。 生2:7、13。 生3:2、4 通过多种不同形式的练习,培养学生运用所学知识解决问题的能力,体现数学的应用价值。
环节三 拓展练习 二、提升练习 1.算一算: (1)奇数与奇数的积是奇数还是偶数 (2)奇数与偶数的积是奇数还是偶数 (3)偶数与偶数的积呢 提问:可以怎么研究? 2.找一找: 小虎在侦破一个案件时发现了一个保险箱。保险箱设有六位数的密码。已知: A是5最大的因数; B的所有因数是1,2,4,8; C是最小的自然数; D只有一个因数; E既是质数又是偶数; F既是9的因数又是9的倍数。 3.试一试: 老师报出一个大于2的偶数,你能找出和为此数的两个质数吗? 例:4=2+2,8=3+5 提问:你能试试看下面这几个数吗? 10, 12, 14, 16, 18, 20 师:介绍哥德巴赫猜想。是不是所有大于2的偶数,都可以表示为两个质数的和呢? 生:举例子探究。 生:奇数×奇数 = 奇数 奇数×偶数 = 偶数 偶数×偶数 = 偶数 生:A是5,因为5的最大因数是它本身; B是8,8有四个因数,它的最大因数也是8; C是0,0是最小的自然数; D是1,1的因数只有1; E是2,偶数中只有2是质数; F是9,一个数是它自己的最大因数,又是自己的最小倍数。所以密码是580129。 生:10=3+7=5+5,12=5+7 14=3+11=7+7 16=3+13=5+11, 18=5+13=7+11, 20=3+17=7+13 选取3道探究的题型,鼓励学生自主探究,积极思考,养成勇于探究乐于思考的精神。
环节四 课堂小结 你有什么收获? 生1:复习了因数、倍数、质数、合数有关的知识。 生2:理清了知识点之间的联系。 鼓励学生畅谈自己的收获和体会,小结课堂,提升总结、表达能力。
环节五 布置作业 教材P16 练习四第5题
