北师大新版八年级(下)《第1章 三角形的证明》常考题套卷(5)(word版含答案)
文档属性
| 名称 | 北师大新版八年级(下)《第1章 三角形的证明》常考题套卷(5)(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 460.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 17:01:27 | ||
图片预览



文档简介
北师大新版八年级(下)《第1章 三角形的证明》常考题套卷(5)
一、选择题(共10小题)
1.对“等角对等边”这句话的理解,正确的是( )
A.只要两个角相等,那么它们所对的边也相等
B.在两个三角形中,如果有两个角相等,那么它们所对的边也相等
C.在一个三角形中,如果有两个角相等,那么它们所对的边也相等
D.以上说法都是正确的
2.已知等腰三角形的周长为17cm,一边长为4cm,则它的腰长为( )
A.4cm B.6.5cm C.6.5cm或9cm D.4cm或6.5cm
3.下列命题中的假命题是( )
A.过直线外一点有且只有一条直线与这条直线平行
B.平行于同一直线的两条直线平行
C.直线y=2x﹣1与直线y=2x+3一定互相平行
D.如果两个角的两边分别平行,那么这两个角相等
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC
5.如图,在△ABC中,AB=AC,∠APB≠∠APC,求证:PB≠PC,当用反证法证明时,第一步应假设( )
A.AB≠AC B.PB=PC C.∠APB=∠APC D.∠B≠∠C
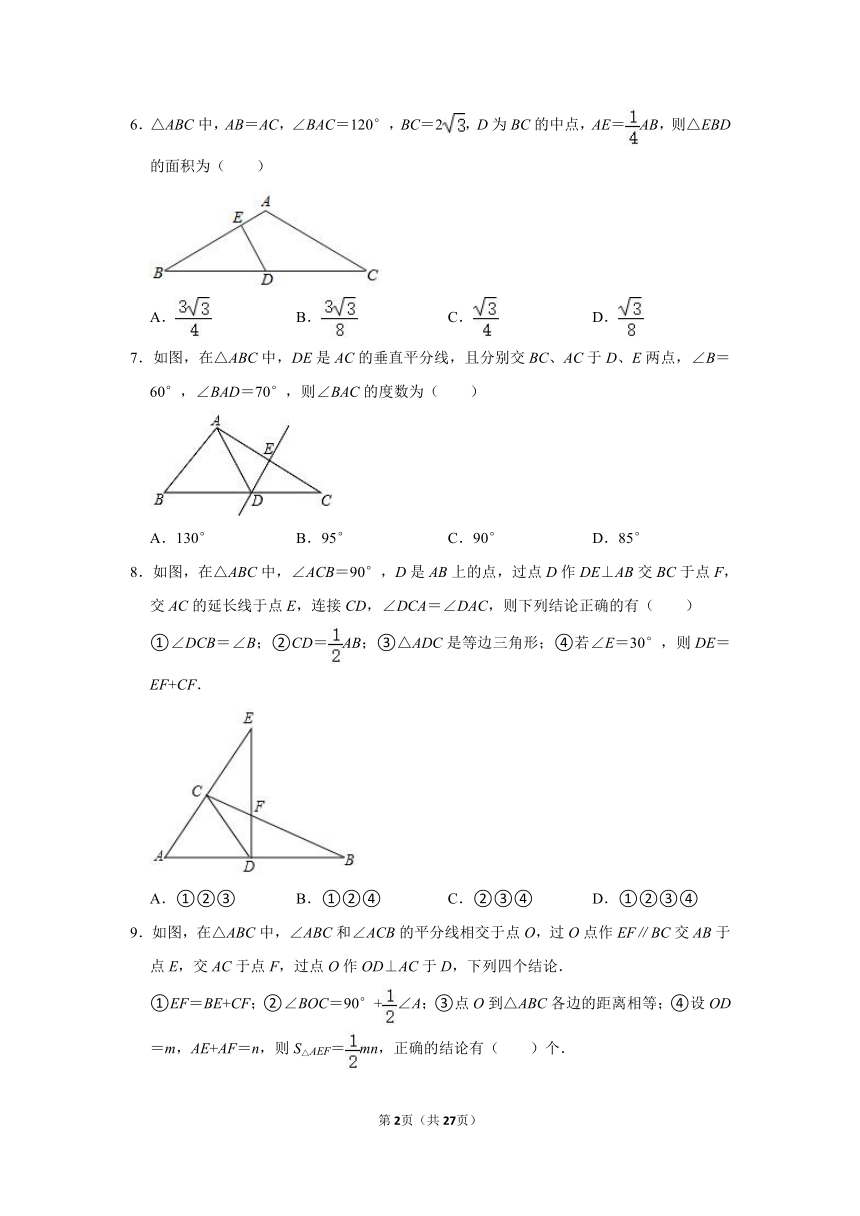
6.△ABC中,AB=AC,∠BAC=120°,BC=2,D为BC的中点,AE=AB,则△EBD的面积为( )
A. B. C. D.
7.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,∠B=60°,∠BAD=70°,则∠BAC的度数为( )
A.130° B.95° C.90° D.85°
8.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
9.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论.
①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn,正确的结论有( )个.
A.1个 B.2个 C.3个 D.4个
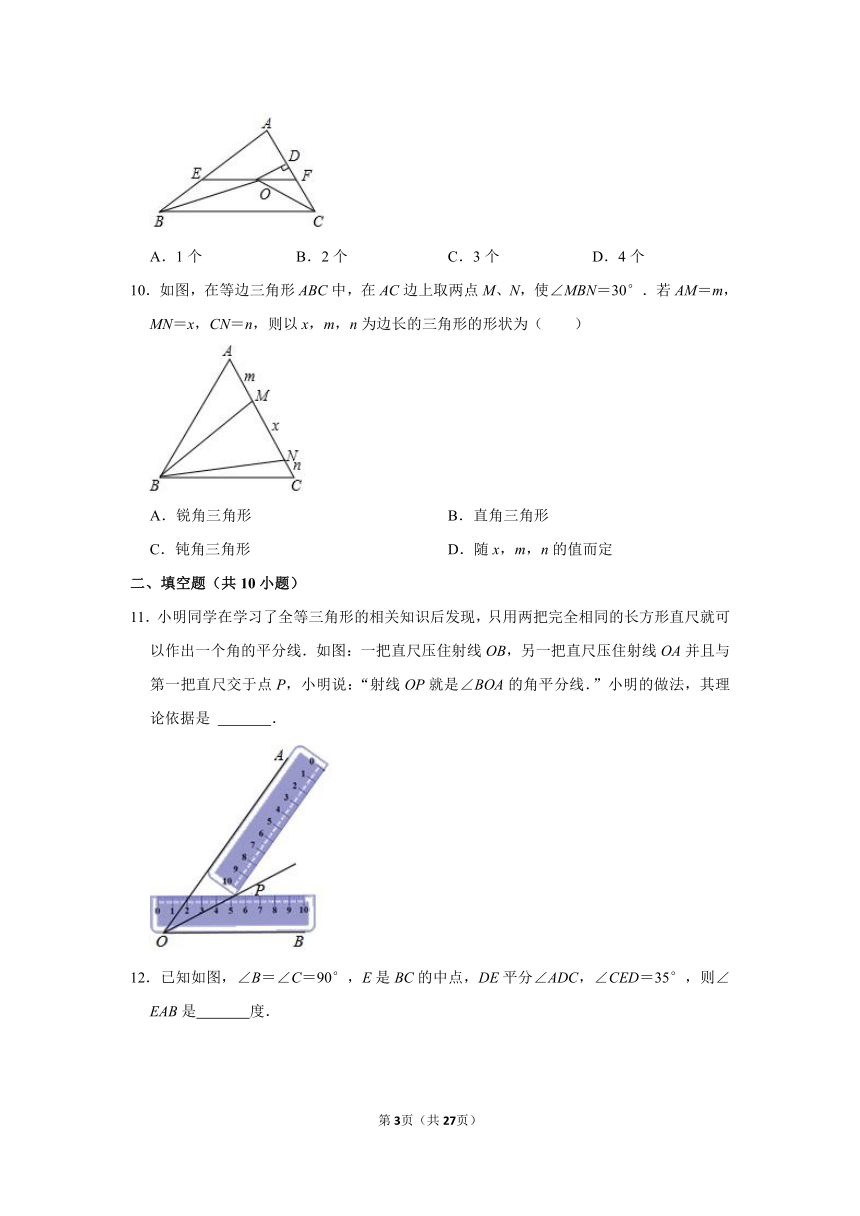
10.如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.随x,m,n的值而定
二、填空题(共10小题)
11.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是 .
12.已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是 度.
13.将命题“同角的补角相等”改写成“如果…那么…”形式为 .
14.在△ABC中,AB=AC,∠A=40°,则∠B的度数为 °.
15.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为40°,则∠B= .
16.在Rt△ABC中,∠C=90°,∠A=30°,AB=6cm,则BC= cm.
17.如图,∠AOB=50°,点P是边OB上一个动点(不与点O重合),当∠A的度数为 时,△AOP为直角三角形.
18.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 .
19.如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .
20.已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 条.
三、解答题(共10小题)
21.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
22.如图,在△ABC中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A的度数.
23.如图,在△ABC中,AB=AD=DC,∠BAD=20°,求∠C的度数?
24.a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留痕迹.
25.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形(请画出图形,写出已知、求证、证明的过程).
26.阅读下面材料:
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
例如要判断命题“相等的角是对顶角”是假命题,可以举出如下反例:
如图,OC是∠AOB的平分线,∠1=∠2,但它们不是对顶角.
请你举出一个反例说明命题“如果两个角的两边分别平行,那么这两个角相等”是假命题.(要求:画出相应的图形,并用文字语言或符号语言表述所举反例)
27.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD.
(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当α为多少度时,△AOD是等腰三角形?
28.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
29.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
30.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
北师大新版八年级(下)《第1章 三角形的证明》常考题套卷(5)
参考答案与试题解析
一、选择题(共10小题)
1.对“等角对等边”这句话的理解,正确的是( )
A.只要两个角相等,那么它们所对的边也相等
B.在两个三角形中,如果有两个角相等,那么它们所对的边也相等
C.在一个三角形中,如果有两个角相等,那么它们所对的边也相等
D.以上说法都是正确的
【解答】解:“等角对等边”是等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等的简写形式,意思是:在一个三角形中,如果有两个角相等,那么它们所对的边也相等.故C正确;
A、B可以举反例说明,如图:DE∥BC,∠ADE=∠B,但AE≠AC.故A、B都错误;故D也错误.
故选:C.
2.已知等腰三角形的周长为17cm,一边长为4cm,则它的腰长为( )
A.4cm B.6.5cm C.6.5cm或9cm D.4cm或6.5cm
【解答】解:①若4cm是腰长,则底边长为:20﹣4﹣4=12(cm),
∵4+4<12,不能组成三角形,舍去;
②若4cm是底边长,则腰长为:=6.5(cm).
则腰长为6.5cm.
故选:B.
3.下列命题中的假命题是( )
A.过直线外一点有且只有一条直线与这条直线平行
B.平行于同一直线的两条直线平行
C.直线y=2x﹣1与直线y=2x+3一定互相平行
D.如果两个角的两边分别平行,那么这两个角相等
【解答】解:A、过直线外一点有且只有一条直线与这条直线平行,正确.
B、平行于同一直线的两条直线平行,正确;
C、直线y=2x﹣1与直线y=2x+3一定互相平行,正确;
D、如果两个角的两边分别平行,那么这两个角相等,错误;应该是如果两个角的两边分别平行,那么这两个角相等或互补;
故选:D.
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC
【解答】解:条件是AB=CD,
理由是:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴Rt△ABE≌Rt△DCF(HL),
故选:D.
5.如图,在△ABC中,AB=AC,∠APB≠∠APC,求证:PB≠PC,当用反证法证明时,第一步应假设( )
A.AB≠AC B.PB=PC C.∠APB=∠APC D.∠B≠∠C
【解答】解:假设结论PB≠PC不成立,即:PB=PC成立.
故选:B.
6.△ABC中,AB=AC,∠BAC=120°,BC=2,D为BC的中点,AE=AB,则△EBD的面积为( )
A. B. C. D.
【解答】解:连接AD,作EF⊥BC于F,
∵AB=AC,∠BAC=120°,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,∠B=∠C=30°
在Rt△ABD中,BD=BC=,∠B=30°,
∴AB===2,
∴AD==1,
∵AE=AB,
∴=,
∵EF⊥BC,AD⊥BC,
∴EF∥AD,
∴△BEF∽△BAD,
∴=,
∴
∴EF=,
∴S△BDE===,
故选:B.
7.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,∠B=60°,∠BAD=70°,则∠BAC的度数为( )
A.130° B.95° C.90° D.85°
【解答】解:∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C,
∵∠B=60°,∠BAD=70°,
∴∠BDA=50°,
∴∠DAC=∠BDA=25°,
∴∠BAC=∠BAD+∠DAC=70°+25°=95°
故选:B.
8.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
【解答】解:∵在△ABC中,∠ACB=90°,DE⊥AB,
∴∠ADE=∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠DCB=90°,
∵∠DCA=∠DAC,
∴AD=CD,∠DCB=∠B;故①正确;
∴CD=BD,
∵AD=CD,
∴CD=AB;故②正确;
∠DCA=∠DAC,
∴AD=CD,
但不能判定△ADC是等边三角形;故③错误;
∵若∠E=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴∠ADC=60°,
∵∠ADE=∠ACB=90°,
∴∠EDC=∠BCD=∠B=30°,
∴CF=DF,
∴DE=EF+DF=EF+CF.故④正确.
故选:B.
9.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论.
①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn,正确的结论有( )个.
A.1个 B.2个 C.3个 D.4个
【解答】解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=AE OM+AF OD=OD (AE+AF)=mn;故④正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故选:D.
10.如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.随x,m,n的值而定
【解答】解:将△ABM绕点B顺时针旋转60°得到△CBH.连接HN.
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,
∵∠MBN=30°,
∴∠ABM+∠CBN=30°,
∴∠NBH=∠CBH+∠CBN=30°,
∴∠NBM=∠NBH,
∵BM=BH,BN=BN,
∴△NBM≌△NBH,
∴MN=NH=x,
∵∠BCH=∠A=60°,CH=AM=n,
∴∠NCH=120°,
∴x,m,n为边长的三角形△NCH是钝角三角形,
故选:C.
二、填空题(共10小题)
11.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是 在角的内部,到角两边距离相等的点在角的平分线上 .
【解答】解:如图所示:过两把直尺的交点P作PE⊥AO,PF⊥BO,
∵两把完全相同的长方形直尺,
∴PE=PF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),
故答案为:在角的内部,到角两边距离相等的点在角的平分线上.
12.已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是 35 度.
【解答】解:过点E作EF⊥AD,
∵DE平分∠ADC,且E是BC的中点,
∴CE=EB=EF,
又∵∠B=90°,且AE=AE,
∴△ABE≌△AFE,
∴∠EAB=∠EAF.
又∵∠CED=35°,∠C=90°,
∴∠CDE=90°﹣35°=55°,
∴∠CDA=110°,
∵∠B=∠C=90°,
∴DC∥AB,
∴∠CDA+∠DAB=180°,
∴∠DAB=70°,
∴∠EAB=35°.
故答案为:35.
13.将命题“同角的补角相等”改写成“如果…那么…”形式为 如果两个角是同一个角的补角,那么这两个角相等 .
【解答】解:“同角的补角相等”的条件是:两个角是同一个角的补角,结论是:这两个角相等.
则将命题“同角的补角相等”改写成“如果…那么…”形式为:如果两个角是同一个角的补角,那么这两个角相等.
故答案是:如果两个角是同一个角的补角,那么这两个角相等.
14.在△ABC中,AB=AC,∠A=40°,则∠B的度数为 70 °.
【解答】解:∵AB=AC,
∴∠B=∠C,
∵∠A=40°,
∴∠B=(180°﹣40°)÷2=70°.
故答案为:70.
15.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为40°,则∠B= 65°或25° .
【解答】解:(1)当AB的中垂线MN与AC相交时,
∵∠AMD=90°,
∴∠A=90°﹣40°=50°,
∵AB=AC,
∴∠B=∠C=(180°﹣∠A)=65°;
(2)当AB的中垂线MN与CA的延长线相交时,
∴∠DAB=90°﹣40°=50°,
∵AB=AC,
∴∠B=∠C=∠DAB=25°.
故答案为65°或25°.
16.在Rt△ABC中,∠C=90°,∠A=30°,AB=6cm,则BC= 3 cm.
【解答】
解:∵在Rt△ABC中,∠C=90°,∠A=30°,AB=6cm,
∴BC=AB=3cm,
故答案为:3.
17.如图,∠AOB=50°,点P是边OB上一个动点(不与点O重合),当∠A的度数为 90°或40° 时,△AOP为直角三角形.
【解答】解:若△AOP为直角三角形,则
①∠A=90°时,△AOP为直角三角形;
②当∠APO=90°时,△AOP为直角三角形,此时∠A=40°.
故答案为90°或40°.
18.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 AC=DE .
【解答】解:AC=DE,
理由是:∵AB⊥DC,
∴∠ABC=∠DBE=90°,
在Rt△ABC和Rt△DBE中,
,
∴Rt△ABC≌Rt△DBE(HL).
故答案为:AC=DE.
19.如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 2n﹣1 .
【解答】解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:△AnBnAn+1的边长为 2n﹣1.
故答案是:2n﹣1.
20.已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 7 条.
【解答】解:如图所示:
当BC1=AC1,AC=CC2,AB=BC3,AC4=CC4,AB=AC5,AB=AC6,BC7=CC7时,都能得到符合题意的等腰三角形.
故答案为:7.
三、解答题(共10小题)
21.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
【解答】解:如图,点P为所作.
22.如图,在△ABC中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A的度数.
【解答】(1)证明:∵CD是∠ACB的平分线,
∴∠BCD=∠ECD.
∵DE∥BC,
∴∠EDC=∠BCD,
∴∠EDC=∠ECD,
∴DE=CE.
(2)解:∵∠ECD=∠EDC=35°,
∴∠ACB=2∠ECD=70°.
∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠A=180°﹣70°﹣70°=40°.
23.如图,在△ABC中,AB=AD=DC,∠BAD=20°,求∠C的度数?
【解答】解:∵∠BAD=20°,AB=AD=DC,
∴∠ABD=∠ADB=80°,
由三角形外角与外角性质可得∠ADC=180°﹣∠ADB=100°,
又∵AD=DC,
∴∠C=∠ADB=40°,
∴∠C=40°.
24.a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留痕迹.
【解答】解:①以A为圆心,以任意长为半径画圆,分别交铁路a和公路b于点B、C;
②分别以B、C为圆心,以大于BC为半径画圆,两圆相交于点D,连接AD,则直线AD即为∠BAC的平分线
③连接MN,分别以M、N为圆心,以大于MN为半径画圆,两圆相交于E、F,连接EF,则直线EF即为线段MN的垂直平分线;
④直线EF与直线AD相交于点O,则点O即为所求点.
同法点O′也满足条件.
故答案为O或O′处.
25.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形(请画出图形,写出已知、求证、证明的过程).
【解答】
已知:如图:∠DAC是△ABC的外角,
AE平分∠DAC,AE∥BC.
求证:△ABC为等腰三角形.
证明:∵AE∥BC,
∴∠EAD=∠B,
∠EAC=∠C,
∵AE平分∠DAC,
∴∠EAD=∠EAC,
∴∠B=∠C,
∴AB=AC,
∴△ABC为等腰三角形.
26.阅读下面材料:
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
例如要判断命题“相等的角是对顶角”是假命题,可以举出如下反例:
如图,OC是∠AOB的平分线,∠1=∠2,但它们不是对顶角.
请你举出一个反例说明命题“如果两个角的两边分别平行,那么这两个角相等”是假命题.(要求:画出相应的图形,并用文字语言或符号语言表述所举反例)
【解答】解:如图,
∠1+∠2=180°;
如果两个角的两边分别平行,那么这两个角相等或互补.
27.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD.
(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当α为多少度时,△AOD是等腰三角形?
【解答】解:(1)∵△OCD是等边三角形,
∴OC=CD,
而△ABC是等边三角形,
∴BC=AC,
∵∠ACB=∠OCD=60°,
∴∠BCO=∠ACD,
在△BOC与△ADC中,
∵,
∴△BOC≌△ADC,
∴∠BOC=∠ADC,
而∠BOC=α=150°,∠ODC=60°,
∴∠ADO=150°﹣60°=90°,
∴△ADO是直角三角形;
(2)∵设∠CBO=∠CAD=a,∠ABO=b,∠BAO=c,∠CAO=d,
则a+b=60°,b+c=180°﹣110°=70°,c+d=60°,
∴b﹣d=10°,
∴(60°﹣a)﹣d=10°,
∴a+d=50°,
即∠DAO=50°,
①要使AO=AD,需∠AOD=∠ADO,
∴190°﹣α=α﹣60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO,
∴110°+80°+60°+α=360°
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD,
110°+50°+60°+α=360°,
∴α=140°.
所以当α为110°、125°、140°时,三角形AOD是等腰三角形.
28.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
【解答】证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD﹣CD=BF﹣EF.
即BC=BE.
29.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
【解答】解:在Rt△ABF中,∠A=70°,CE,BF是两条高,
∴∠EBF=20°,∠ECA=20°,
又∵∠BCE=30°,
∴∠ACB=50°,
∴在Rt△BCF中∠FBC=40°.
30.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
【解答】解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
第1页(共3页)
一、选择题(共10小题)
1.对“等角对等边”这句话的理解,正确的是( )
A.只要两个角相等,那么它们所对的边也相等
B.在两个三角形中,如果有两个角相等,那么它们所对的边也相等
C.在一个三角形中,如果有两个角相等,那么它们所对的边也相等
D.以上说法都是正确的
2.已知等腰三角形的周长为17cm,一边长为4cm,则它的腰长为( )
A.4cm B.6.5cm C.6.5cm或9cm D.4cm或6.5cm
3.下列命题中的假命题是( )
A.过直线外一点有且只有一条直线与这条直线平行
B.平行于同一直线的两条直线平行
C.直线y=2x﹣1与直线y=2x+3一定互相平行
D.如果两个角的两边分别平行,那么这两个角相等
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC
5.如图,在△ABC中,AB=AC,∠APB≠∠APC,求证:PB≠PC,当用反证法证明时,第一步应假设( )
A.AB≠AC B.PB=PC C.∠APB=∠APC D.∠B≠∠C
6.△ABC中,AB=AC,∠BAC=120°,BC=2,D为BC的中点,AE=AB,则△EBD的面积为( )
A. B. C. D.
7.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,∠B=60°,∠BAD=70°,则∠BAC的度数为( )
A.130° B.95° C.90° D.85°
8.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
9.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论.
①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn,正确的结论有( )个.
A.1个 B.2个 C.3个 D.4个
10.如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.随x,m,n的值而定
二、填空题(共10小题)
11.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是 .
12.已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是 度.
13.将命题“同角的补角相等”改写成“如果…那么…”形式为 .
14.在△ABC中,AB=AC,∠A=40°,则∠B的度数为 °.
15.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为40°,则∠B= .
16.在Rt△ABC中,∠C=90°,∠A=30°,AB=6cm,则BC= cm.
17.如图,∠AOB=50°,点P是边OB上一个动点(不与点O重合),当∠A的度数为 时,△AOP为直角三角形.
18.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 .
19.如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 .
20.已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 条.
三、解答题(共10小题)
21.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
22.如图,在△ABC中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A的度数.
23.如图,在△ABC中,AB=AD=DC,∠BAD=20°,求∠C的度数?
24.a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留痕迹.
25.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形(请画出图形,写出已知、求证、证明的过程).
26.阅读下面材料:
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
例如要判断命题“相等的角是对顶角”是假命题,可以举出如下反例:
如图,OC是∠AOB的平分线,∠1=∠2,但它们不是对顶角.
请你举出一个反例说明命题“如果两个角的两边分别平行,那么这两个角相等”是假命题.(要求:画出相应的图形,并用文字语言或符号语言表述所举反例)
27.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD.
(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当α为多少度时,△AOD是等腰三角形?
28.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
29.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
30.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
北师大新版八年级(下)《第1章 三角形的证明》常考题套卷(5)
参考答案与试题解析
一、选择题(共10小题)
1.对“等角对等边”这句话的理解,正确的是( )
A.只要两个角相等,那么它们所对的边也相等
B.在两个三角形中,如果有两个角相等,那么它们所对的边也相等
C.在一个三角形中,如果有两个角相等,那么它们所对的边也相等
D.以上说法都是正确的
【解答】解:“等角对等边”是等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等的简写形式,意思是:在一个三角形中,如果有两个角相等,那么它们所对的边也相等.故C正确;
A、B可以举反例说明,如图:DE∥BC,∠ADE=∠B,但AE≠AC.故A、B都错误;故D也错误.
故选:C.
2.已知等腰三角形的周长为17cm,一边长为4cm,则它的腰长为( )
A.4cm B.6.5cm C.6.5cm或9cm D.4cm或6.5cm
【解答】解:①若4cm是腰长,则底边长为:20﹣4﹣4=12(cm),
∵4+4<12,不能组成三角形,舍去;
②若4cm是底边长,则腰长为:=6.5(cm).
则腰长为6.5cm.
故选:B.
3.下列命题中的假命题是( )
A.过直线外一点有且只有一条直线与这条直线平行
B.平行于同一直线的两条直线平行
C.直线y=2x﹣1与直线y=2x+3一定互相平行
D.如果两个角的两边分别平行,那么这两个角相等
【解答】解:A、过直线外一点有且只有一条直线与这条直线平行,正确.
B、平行于同一直线的两条直线平行,正确;
C、直线y=2x﹣1与直线y=2x+3一定互相平行,正确;
D、如果两个角的两边分别平行,那么这两个角相等,错误;应该是如果两个角的两边分别平行,那么这两个角相等或互补;
故选:D.
4.如图,BE=CF,AE⊥BC,DF⊥BC,要根据“HL”证明Rt△ABE≌Rt△DCF,则还需要添加一个条件是( )
A.AE=DF B.∠A=∠D C.∠B=∠C D.AB=DC
【解答】解:条件是AB=CD,
理由是:∵AE⊥BC,DF⊥BC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△DCF中,
,
∴Rt△ABE≌Rt△DCF(HL),
故选:D.
5.如图,在△ABC中,AB=AC,∠APB≠∠APC,求证:PB≠PC,当用反证法证明时,第一步应假设( )
A.AB≠AC B.PB=PC C.∠APB=∠APC D.∠B≠∠C
【解答】解:假设结论PB≠PC不成立,即:PB=PC成立.
故选:B.
6.△ABC中,AB=AC,∠BAC=120°,BC=2,D为BC的中点,AE=AB,则△EBD的面积为( )
A. B. C. D.
【解答】解:连接AD,作EF⊥BC于F,
∵AB=AC,∠BAC=120°,D为BC的中点,
∴AD⊥BC,AD平分∠BAC,∠B=∠C=30°
在Rt△ABD中,BD=BC=,∠B=30°,
∴AB===2,
∴AD==1,
∵AE=AB,
∴=,
∵EF⊥BC,AD⊥BC,
∴EF∥AD,
∴△BEF∽△BAD,
∴=,
∴
∴EF=,
∴S△BDE===,
故选:B.
7.如图,在△ABC中,DE是AC的垂直平分线,且分别交BC、AC于D、E两点,∠B=60°,∠BAD=70°,则∠BAC的度数为( )
A.130° B.95° C.90° D.85°
【解答】解:∵DE是AC的垂直平分线,
∴DA=DC,
∴∠DAC=∠C,
∵∠B=60°,∠BAD=70°,
∴∠BDA=50°,
∴∠DAC=∠BDA=25°,
∴∠BAC=∠BAD+∠DAC=70°+25°=95°
故选:B.
8.如图,在△ABC中,∠ACB=90°,D是AB上的点,过点D作DE⊥AB交BC于点F,交AC的延长线于点E,连接CD,∠DCA=∠DAC,则下列结论正确的有( )
①∠DCB=∠B;②CD=AB;③△ADC是等边三角形;④若∠E=30°,则DE=EF+CF.
A.①②③ B.①②④ C.②③④ D.①②③④
【解答】解:∵在△ABC中,∠ACB=90°,DE⊥AB,
∴∠ADE=∠ACB=90°,
∴∠A+∠B=90°,∠ACD+∠DCB=90°,
∵∠DCA=∠DAC,
∴AD=CD,∠DCB=∠B;故①正确;
∴CD=BD,
∵AD=CD,
∴CD=AB;故②正确;
∠DCA=∠DAC,
∴AD=CD,
但不能判定△ADC是等边三角形;故③错误;
∵若∠E=30°,
∴∠A=60°,
∴△ACD是等边三角形,
∴∠ADC=60°,
∵∠ADE=∠ACB=90°,
∴∠EDC=∠BCD=∠B=30°,
∴CF=DF,
∴DE=EF+DF=EF+CF.故④正确.
故选:B.
9.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点O,过O点作EF∥BC交AB于点E,交AC于点F,过点O作OD⊥AC于D,下列四个结论.
①EF=BE+CF;②∠BOC=90°+∠A;③点O到△ABC各边的距离相等;④设OD=m,AE+AF=n,则S△AEF=mn,正确的结论有( )个.
A.1个 B.2个 C.3个 D.4个
【解答】解:∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠ABC,∠OCB=∠ACB,∠A+∠ABC+∠ACB=180°,
∴∠OBC+∠OCB=90°﹣∠A,
∴∠BOC=180°﹣(∠OBC+∠OCB)=90°+∠A;故②正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴∠OBC=∠OBE,∠OCB=∠OCF,
∵EF∥BC,
∴∠OBC=∠EOB,∠OCB=∠FOC,
∴∠EOB=∠OBE,∠FOC=∠OCF,
∴BE=OE,CF=OF,
∴EF=OE+OF=BE+CF,
故①正确;
过点O作OM⊥AB于M,作ON⊥BC于N,连接OA,
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴ON=OD=OM=m,
∴S△AEF=S△AOE+S△AOF=AE OM+AF OD=OD (AE+AF)=mn;故④正确;
∵在△ABC中,∠ABC和∠ACB的平分线相交于点O,
∴点O到△ABC各边的距离相等,故③正确.
故选:D.
10.如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.随x,m,n的值而定
【解答】解:将△ABM绕点B顺时针旋转60°得到△CBH.连接HN.
∵△ABC是等边三角形,
∴∠ABC=∠ACB=∠A=60°,
∵∠MBN=30°,
∴∠ABM+∠CBN=30°,
∴∠NBH=∠CBH+∠CBN=30°,
∴∠NBM=∠NBH,
∵BM=BH,BN=BN,
∴△NBM≌△NBH,
∴MN=NH=x,
∵∠BCH=∠A=60°,CH=AM=n,
∴∠NCH=120°,
∴x,m,n为边长的三角形△NCH是钝角三角形,
故选:C.
二、填空题(共10小题)
11.小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”小明的做法,其理论依据是 在角的内部,到角两边距离相等的点在角的平分线上 .
【解答】解:如图所示:过两把直尺的交点P作PE⊥AO,PF⊥BO,
∵两把完全相同的长方形直尺,
∴PE=PF,
∴OP平分∠AOB(角的内部到角的两边的距离相等的点在这个角的平分线上),
故答案为:在角的内部,到角两边距离相等的点在角的平分线上.
12.已知如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB是 35 度.
【解答】解:过点E作EF⊥AD,
∵DE平分∠ADC,且E是BC的中点,
∴CE=EB=EF,
又∵∠B=90°,且AE=AE,
∴△ABE≌△AFE,
∴∠EAB=∠EAF.
又∵∠CED=35°,∠C=90°,
∴∠CDE=90°﹣35°=55°,
∴∠CDA=110°,
∵∠B=∠C=90°,
∴DC∥AB,
∴∠CDA+∠DAB=180°,
∴∠DAB=70°,
∴∠EAB=35°.
故答案为:35.
13.将命题“同角的补角相等”改写成“如果…那么…”形式为 如果两个角是同一个角的补角,那么这两个角相等 .
【解答】解:“同角的补角相等”的条件是:两个角是同一个角的补角,结论是:这两个角相等.
则将命题“同角的补角相等”改写成“如果…那么…”形式为:如果两个角是同一个角的补角,那么这两个角相等.
故答案是:如果两个角是同一个角的补角,那么这两个角相等.
14.在△ABC中,AB=AC,∠A=40°,则∠B的度数为 70 °.
【解答】解:∵AB=AC,
∴∠B=∠C,
∵∠A=40°,
∴∠B=(180°﹣40°)÷2=70°.
故答案为:70.
15.在△ABC中,AB=AC,AB的垂直平分线与AC所在的直线相交所得到锐角为40°,则∠B= 65°或25° .
【解答】解:(1)当AB的中垂线MN与AC相交时,
∵∠AMD=90°,
∴∠A=90°﹣40°=50°,
∵AB=AC,
∴∠B=∠C=(180°﹣∠A)=65°;
(2)当AB的中垂线MN与CA的延长线相交时,
∴∠DAB=90°﹣40°=50°,
∵AB=AC,
∴∠B=∠C=∠DAB=25°.
故答案为65°或25°.
16.在Rt△ABC中,∠C=90°,∠A=30°,AB=6cm,则BC= 3 cm.
【解答】
解:∵在Rt△ABC中,∠C=90°,∠A=30°,AB=6cm,
∴BC=AB=3cm,
故答案为:3.
17.如图,∠AOB=50°,点P是边OB上一个动点(不与点O重合),当∠A的度数为 90°或40° 时,△AOP为直角三角形.
【解答】解:若△AOP为直角三角形,则
①∠A=90°时,△AOP为直角三角形;
②当∠APO=90°时,△AOP为直角三角形,此时∠A=40°.
故答案为90°或40°.
18.如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 AC=DE .
【解答】解:AC=DE,
理由是:∵AB⊥DC,
∴∠ABC=∠DBE=90°,
在Rt△ABC和Rt△DBE中,
,
∴Rt△ABC≌Rt△DBE(HL).
故答案为:AC=DE.
19.如图,∠MON=30°,点A1,A2,A3,…在射线ON上,点B1,B2,B3,…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形.若OA1=1,则△AnBnAn+1的边长为 2n﹣1 .
【解答】解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=1,
∴A2B1=1,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=4,
A4B4=8B1A2=8,
A5B5=16B1A2=16,
以此类推:△AnBnAn+1的边长为 2n﹣1.
故答案是:2n﹣1.
20.已知△ABC的三条边长分别为3,4,6,在△ABC所在平面内画一条直线,将△ABC分割成两个三角形,使其中的一个是等腰三角形,则这样的直线最多可画 7 条.
【解答】解:如图所示:
当BC1=AC1,AC=CC2,AB=BC3,AC4=CC4,AB=AC5,AB=AC6,BC7=CC7时,都能得到符合题意的等腰三角形.
故答案为:7.
三、解答题(共10小题)
21.如图:已知OA和OB两条公路,以及C、D两个村庄,建立一个车站P,使车站到两个村庄距离相等即PC=PD,且P到OA,OB两条公路的距离相等.
【解答】解:如图,点P为所作.
22.如图,在△ABC中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A的度数.
【解答】(1)证明:∵CD是∠ACB的平分线,
∴∠BCD=∠ECD.
∵DE∥BC,
∴∠EDC=∠BCD,
∴∠EDC=∠ECD,
∴DE=CE.
(2)解:∵∠ECD=∠EDC=35°,
∴∠ACB=2∠ECD=70°.
∵AB=AC,
∴∠ABC=∠ACB=70°,
∴∠A=180°﹣70°﹣70°=40°.
23.如图,在△ABC中,AB=AD=DC,∠BAD=20°,求∠C的度数?
【解答】解:∵∠BAD=20°,AB=AD=DC,
∴∠ABD=∠ADB=80°,
由三角形外角与外角性质可得∠ADC=180°﹣∠ADB=100°,
又∵AD=DC,
∴∠C=∠ADB=40°,
∴∠C=40°.
24.a,b分别代表铁路和公路,点M、N分别代表蔬菜和杂货批发市场.现要建中转站O点,使O点到铁路、公路距离相等,且到两市场距离相等.请用尺规画出O点位置,不写作法,保留痕迹.
【解答】解:①以A为圆心,以任意长为半径画圆,分别交铁路a和公路b于点B、C;
②分别以B、C为圆心,以大于BC为半径画圆,两圆相交于点D,连接AD,则直线AD即为∠BAC的平分线
③连接MN,分别以M、N为圆心,以大于MN为半径画圆,两圆相交于E、F,连接EF,则直线EF即为线段MN的垂直平分线;
④直线EF与直线AD相交于点O,则点O即为所求点.
同法点O′也满足条件.
故答案为O或O′处.
25.求证:如果三角形一个外角的平分线平行于三角形的一边,那么这个三角形是等腰三角形(请画出图形,写出已知、求证、证明的过程).
【解答】
已知:如图:∠DAC是△ABC的外角,
AE平分∠DAC,AE∥BC.
求证:△ABC为等腰三角形.
证明:∵AE∥BC,
∴∠EAD=∠B,
∠EAC=∠C,
∵AE平分∠DAC,
∴∠EAD=∠EAC,
∴∠B=∠C,
∴AB=AC,
∴△ABC为等腰三角形.
26.阅读下面材料:
判断一个命题是假命题,只要举出一个例子(反例),它符合命题的题设,但不满足结论就可以了.
例如要判断命题“相等的角是对顶角”是假命题,可以举出如下反例:
如图,OC是∠AOB的平分线,∠1=∠2,但它们不是对顶角.
请你举出一个反例说明命题“如果两个角的两边分别平行,那么这两个角相等”是假命题.(要求:画出相应的图形,并用文字语言或符号语言表述所举反例)
【解答】解:如图,
∠1+∠2=180°;
如果两个角的两边分别平行,那么这两个角相等或互补.
27.如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α.以OC为一边作等边三角形OCD,连接AC、AD.
(1)当α=150°时,试判断△AOD的形状,并说明理由;
(2)探究:当α为多少度时,△AOD是等腰三角形?
【解答】解:(1)∵△OCD是等边三角形,
∴OC=CD,
而△ABC是等边三角形,
∴BC=AC,
∵∠ACB=∠OCD=60°,
∴∠BCO=∠ACD,
在△BOC与△ADC中,
∵,
∴△BOC≌△ADC,
∴∠BOC=∠ADC,
而∠BOC=α=150°,∠ODC=60°,
∴∠ADO=150°﹣60°=90°,
∴△ADO是直角三角形;
(2)∵设∠CBO=∠CAD=a,∠ABO=b,∠BAO=c,∠CAO=d,
则a+b=60°,b+c=180°﹣110°=70°,c+d=60°,
∴b﹣d=10°,
∴(60°﹣a)﹣d=10°,
∴a+d=50°,
即∠DAO=50°,
①要使AO=AD,需∠AOD=∠ADO,
∴190°﹣α=α﹣60°,
∴α=125°;
②要使OA=OD,需∠OAD=∠ADO,
∴110°+80°+60°+α=360°
∴α=110°;
③要使OD=AD,需∠OAD=∠AOD,
110°+50°+60°+α=360°,
∴α=140°.
所以当α为110°、125°、140°时,三角形AOD是等腰三角形.
28.如图,已知AD,AF分别是两个钝角△ABC和△ABE的高,如果AD=AF,AC=AE.
求证:BC=BE.
【解答】证明:∵AD,AF分别是两个钝角△ABC和△ABE的高,且AD=AF,AC=AE,
∴Rt△ADC≌Rt△AFE(HL).
∴CD=EF.
∵AD=AF,AB=AB,
∴Rt△ABD≌Rt△ABF(HL).
∴BD=BF.
∴BD﹣CD=BF﹣EF.
即BC=BE.
29.如图,在△ABC中,CE,BF是两条高,若∠A=70°,∠BCE=30°,求∠EBF与∠FBC的度数.
【解答】解:在Rt△ABF中,∠A=70°,CE,BF是两条高,
∴∠EBF=20°,∠ECA=20°,
又∵∠BCE=30°,
∴∠ACB=50°,
∴在Rt△BCF中∠FBC=40°.
30.等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试说明你的结论.
【解答】解:△APQ为等边三角形.
证明:∵△ABC为等边三角形,
∴AB=AC.
在△ABP与△ACQ中,
∵,
∴△ABP≌△ACQ(SAS).
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.
第1页(共3页)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
