人教版八年级下册19.2.1正比例函数课件(共18张PPT)
文档属性
| 名称 | 人教版八年级下册19.2.1正比例函数课件(共18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 701.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 20:29:18 | ||
图片预览






文档简介
(共19张PPT)
19.2.1 正比例函数
第十九章 一次函数
第2课时 正比例函数的图象和性质
学习目标
【学习目标】
1.会用描点法画正比例函数的图象.
2.掌握正比例函数的图象和性质.
3.会用正比例函数的知识解决简单的实际问题.
【学习重点】
正比例函数的图象和性质.
【学习难点】
正比例函数的图象和性质的应用.
一天,小明以80米/分的速度去上学,请问小明离家的距离s(米)与小明出发的时间t(分)之间的函数关系式是怎样的?
它是正比例函数吗?
函数有哪些表示方法
s=80t(t≥0);
图象法、列表法、解析式法.
是正比例函数;
旧识回顾
正比例函数的图象
在本章第1节的学习中,我们知道函数的表示形式分为三种:图象法,列表法,解析式法.
那么如果已知一个正比例函数,该如何制作它的图象呢?
例1 画出下列正比例函数的图象:(1)y=2x, ;
(2)y=-1.5x,y=-4x.
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
解:(1)函数y=2x中自变量x可为任意实数.
①列表:
新知探究
y=2x
②描点;
③连线.
同样可以画出
函数 的图象.
观察发现:这两个图象都是经过原点的 .
而且都经过第 象限;
一、三
直线
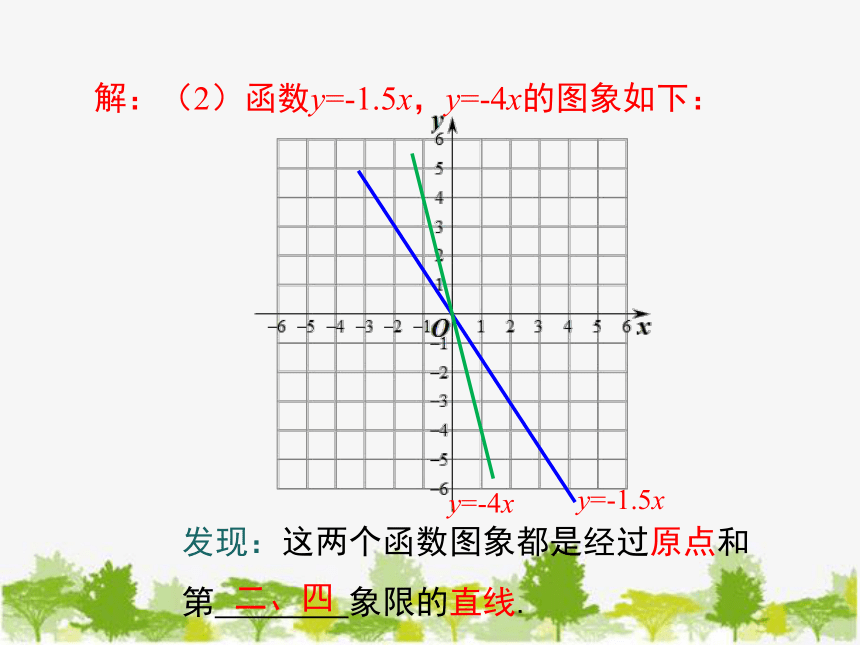
解:(2)函数y=-1.5x,y=-4x的图象如下:
y=-4x
y=-1.5x
发现:这两个函数图象都是经过原点和
第 象限的直线.
二、四
这四个函数图象有什么共同特征,又有什么区别?
y=kx (k是常数,k≠0)的图象是一条经过原点的直线
y=kx(k≠0) 经过的象限
k>0 第一、三象限
k<0 第二、四象限
由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.
怎样画正比例函数的图象最简单?为什么?
新知探究
O
用你认为最简单的方法画出下列函数的图象:
(1) y=-3x;(2)
x 0 1
y=-3x
0
-3
0
y=-3x
新知探究
(1)若函数图象经过第一、三象限,则k的取值范围是_____.
例2 已知正比例函数y=(k+1)x.
k>-1
(2)若函数图象经过点(2,4),则k_____.
解析:因为函数图象经过第一、三象限,所以k+1>0,
解得k>-1.
解析:将坐标(2,4)带入函数解析式中,得4=(k+1)·2,
解得k=1.
=1
新知探究
正比例函数的性质
问题:在同一直角坐标系内画出正比例函数 y=x , y=3x,
y=- x和 y=-4x 的图象.
这四个函数中,随着x的增大,y的值分别如何变化
总结归纳
在正比例函数y=kx(k≠0)中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
|k|越大,直线越陡,
直线越靠近y轴.
|k|越小,直线越平缓,直线越靠近X轴。
1. 已知正比例函数y=kx (k>0)的图象上有两点(x1,y1),(x2,y2),若x1<
分析:因为当k>0时,y的值随着x值的增大而增大,
所以x1针对练习
2. 已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
解:因为正比例函数y=mx的图象经过点(m,4),
所以4=m·m,解得m=±2.
又y的值随着x值的增大而减小,
所以m<0,故m=-2
针对练习
B
2.对于正比例函数y =(k-2)x,当x 增大时,y 随x 的增大而增大,则k的取值范围 ( )
A.k<2 B.k≤2 C.k>2 D.k≥2
C
1.下列图象哪个可能是函数y=-x的图象( )
A.
B.
C.
D.
随堂练习
4.已知正比例函数y=(2m+4)x.
(1)当m ,函数图象经过第一、三象限;
(2)当m ,y 随x 的增大而减小;
(3)当m ,函数图象经过点(2,10).
>-2
<-2
=0.5
3.函数y=-7x的图象经过第_________象限,经过点_______
与点 ,y随x的增大而_______.
二、四
(0,0)
(1,-7)
减小
随堂练习
5. 比较大小:
(1)k1 k2;(2)k3 k4;
(3)比较k1, k2, k3, k4大小,并用不等号连接.
<
解: k1<k2 <k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
随堂练习
通过今天的学习,
能说说你的收获和体会吗
你有什么经验与收获让同学们共享呢?
回顾反思
正比例函数的图象和性质
图象:经过原点的直线.
当k>0时,经过第一、三象限;当k<0时,经过第二、四象限.
性质:当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
课堂小结
19.2.1 正比例函数
第十九章 一次函数
第2课时 正比例函数的图象和性质
学习目标
【学习目标】
1.会用描点法画正比例函数的图象.
2.掌握正比例函数的图象和性质.
3.会用正比例函数的知识解决简单的实际问题.
【学习重点】
正比例函数的图象和性质.
【学习难点】
正比例函数的图象和性质的应用.
一天,小明以80米/分的速度去上学,请问小明离家的距离s(米)与小明出发的时间t(分)之间的函数关系式是怎样的?
它是正比例函数吗?
函数有哪些表示方法
s=80t(t≥0);
图象法、列表法、解析式法.
是正比例函数;
旧识回顾
正比例函数的图象
在本章第1节的学习中,我们知道函数的表示形式分为三种:图象法,列表法,解析式法.
那么如果已知一个正比例函数,该如何制作它的图象呢?
例1 画出下列正比例函数的图象:(1)y=2x, ;
(2)y=-1.5x,y=-4x.
x
y
1
0
0
-1
2
-2
…
…
…
…
2
4
-2
-4
解:(1)函数y=2x中自变量x可为任意实数.
①列表:
新知探究
y=2x
②描点;
③连线.
同样可以画出
函数 的图象.
观察发现:这两个图象都是经过原点的 .
而且都经过第 象限;
一、三
直线
解:(2)函数y=-1.5x,y=-4x的图象如下:
y=-4x
y=-1.5x
发现:这两个函数图象都是经过原点和
第 象限的直线.
二、四
这四个函数图象有什么共同特征,又有什么区别?
y=kx (k是常数,k≠0)的图象是一条经过原点的直线
y=kx(k≠0) 经过的象限
k>0 第一、三象限
k<0 第二、四象限
由于两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k),连线即可.
怎样画正比例函数的图象最简单?为什么?
新知探究
O
用你认为最简单的方法画出下列函数的图象:
(1) y=-3x;(2)
x 0 1
y=-3x
0
-3
0
y=-3x
新知探究
(1)若函数图象经过第一、三象限,则k的取值范围是_____.
例2 已知正比例函数y=(k+1)x.
k>-1
(2)若函数图象经过点(2,4),则k_____.
解析:因为函数图象经过第一、三象限,所以k+1>0,
解得k>-1.
解析:将坐标(2,4)带入函数解析式中,得4=(k+1)·2,
解得k=1.
=1
新知探究
正比例函数的性质
问题:在同一直角坐标系内画出正比例函数 y=x , y=3x,
y=- x和 y=-4x 的图象.
这四个函数中,随着x的增大,y的值分别如何变化
总结归纳
在正比例函数y=kx(k≠0)中,
当k>0时,y的值随着x值的增大而增大;
当k<0时,y的值随着x值的增大而减小.
|k|越大,直线越陡,
直线越靠近y轴.
|k|越小,直线越平缓,直线越靠近X轴。
1. 已知正比例函数y=kx (k>0)的图象上有两点(x1,y1),(x2,y2),若x1
分析:因为当k>0时,y的值随着x值的增大而增大,
所以x1
2. 已知正比例函数y=mx的图象经过点(m,4),且y的值随着x值的增大而减小,求m的值.
解:因为正比例函数y=mx的图象经过点(m,4),
所以4=m·m,解得m=±2.
又y的值随着x值的增大而减小,
所以m<0,故m=-2
针对练习
B
2.对于正比例函数y =(k-2)x,当x 增大时,y 随x 的增大而增大,则k的取值范围 ( )
A.k<2 B.k≤2 C.k>2 D.k≥2
C
1.下列图象哪个可能是函数y=-x的图象( )
A.
B.
C.
D.
随堂练习
4.已知正比例函数y=(2m+4)x.
(1)当m ,函数图象经过第一、三象限;
(2)当m ,y 随x 的增大而减小;
(3)当m ,函数图象经过点(2,10).
>-2
<-2
=0.5
3.函数y=-7x的图象经过第_________象限,经过点_______
与点 ,y随x的增大而_______.
二、四
(0,0)
(1,-7)
减小
随堂练习
5. 比较大小:
(1)k1 k2;(2)k3 k4;
(3)比较k1, k2, k3, k4大小,并用不等号连接.
<
解: k1<k2 <k3 <k4
4
2
-2
-4
4
x
y
O
y =k4 x
-4
-2
2
y =k3 x
y =k2 x
y =k1 x
<
随堂练习
通过今天的学习,
能说说你的收获和体会吗
你有什么经验与收获让同学们共享呢?
回顾反思
正比例函数的图象和性质
图象:经过原点的直线.
当k>0时,经过第一、三象限;当k<0时,经过第二、四象限.
性质:当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
课堂小结
