人教版A版(2019)课标高中数学选择性必修一1.2空间向量的基本定理 学案
文档属性
| 名称 | 人教版A版(2019)课标高中数学选择性必修一1.2空间向量的基本定理 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 164.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 20:58:08 | ||
图片预览

文档简介
空间向量的基本定理
【学习目标】
1.知识目标:了解共线或平行向量概念,向量与平面平行(共面)的意义,掌握它们的表示法;理解共线向量定理,共面向量定理。
2.能力目标:类比平面向量的基本定理学习空间向量基本定理,培养学生类比、联想、维数转换的思想方法和空间想象能力。
3.通过本节课的学习,培养学生的理性精神。
【学习重难点】
重点:空间向量共线和共面的条件。
难点:对这些定理条件的理解与运用。
【学习方法】
自主、合作、探究
【学习过程】
自主学习
1.共线向量定理:两个空间向量、(≠),//的充要条件是存在唯一的实数x,使 。
思考一:(1)≠的原因 。
(2)用共线向量定理证明两直线平行应注意什么问题?
2.共面向量:
已知向量,作,如果的基线 ,则就说向量平行于平面,记作: 。通常我们把平行于同一平面的向量,叫做 。
思考二:(1),的基线一定与平面平行吗?
合作探究
共面向量定理:如果两个向量不共线,与向量共面的充要条件是存在唯一的一对实数使 。
思考三:(1)这个定理的条件和结论分别是什么?
(2)证明其必要性是由谁推出谁?证明其充分性是由谁推出谁?
证明:
思考四:1.若,能不能说明所在的基线都共面?
2.平行向量基本定理与共面向量定理有什么区别?
知识运用
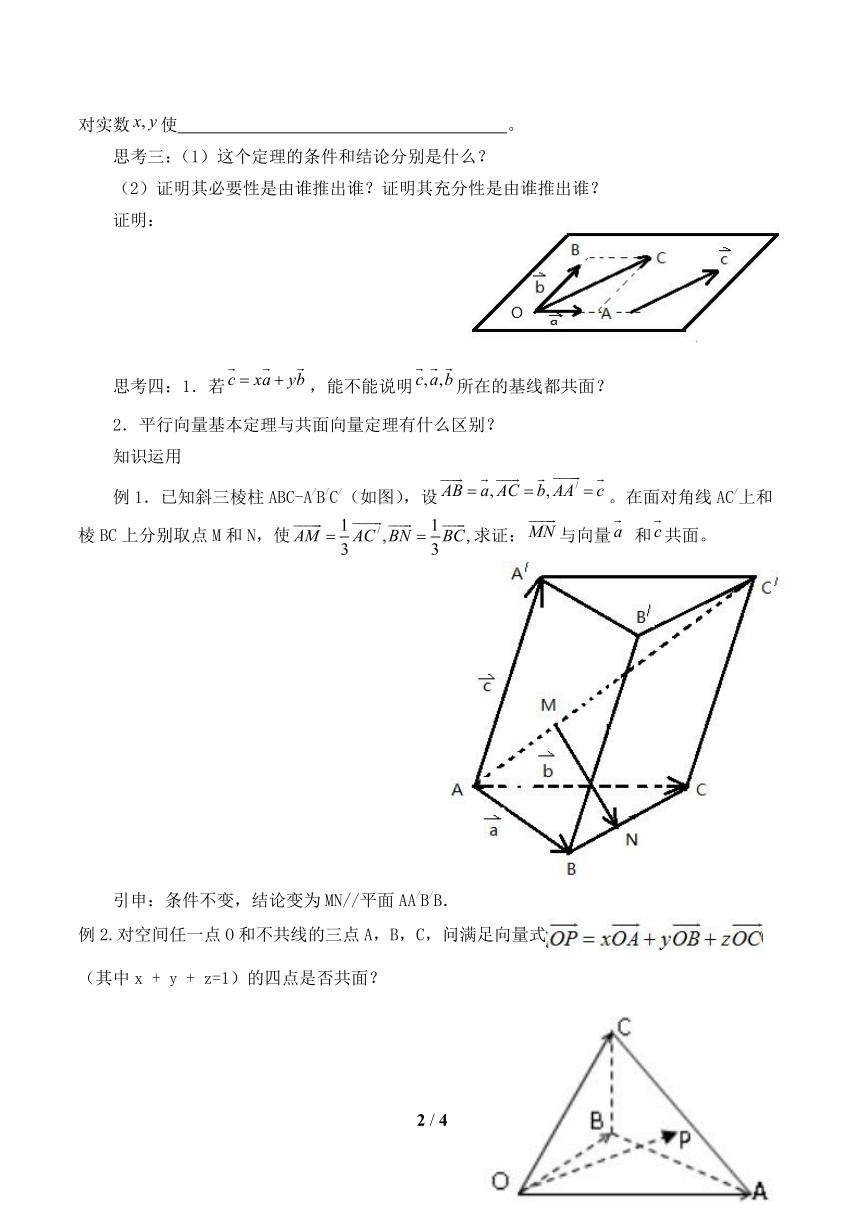
例1.已知斜三棱柱ABC-A/B/C/(如图),设。在面对角线AC/上和棱BC上分别取点M和N,使求证:与向量 和共面。
引申:条件不变,结论变为MN//平面AA/B/B.
例2.对空间任一点O和不共线的三点A,B,C,问满足向量式(其中x + y + z=1)的四点是否共面?
跟踪练习:已知三点不共线,对平面外任一点,满足,试判断:点与是否一定共面?
【达标检测】
已知平行四边形ABCD,从平面外一点引向量,求证:四点E、F、G、H共面;
问题:在平面上,任一向量都能用两个不共线的向量来表示,若空间三个向量不共面,那么空间的任一向量能不能用这三个向量表示。同学们类比平面向量基本定理,
猜想结论:
预习:空间向量分解定理的证明与应用。
1.下列说法正确的是( )
A.与非零向量共线,与共线,则与共线
B. 任意两个相等向量不一定共线
C. 任意两个共线向量相等
D. 若向量与共线,则
2.对于空间中的三个向量,它们一定是:( )
A.共面向量 B.共线向量 C.不共面向量 D.既不共线又不共面向量
3.已知三点不共线,对平面外任一点,满足条件,
试判断:点与是否一定共面?
4.
B
4 / 4
【学习目标】
1.知识目标:了解共线或平行向量概念,向量与平面平行(共面)的意义,掌握它们的表示法;理解共线向量定理,共面向量定理。
2.能力目标:类比平面向量的基本定理学习空间向量基本定理,培养学生类比、联想、维数转换的思想方法和空间想象能力。
3.通过本节课的学习,培养学生的理性精神。
【学习重难点】
重点:空间向量共线和共面的条件。
难点:对这些定理条件的理解与运用。
【学习方法】
自主、合作、探究
【学习过程】
自主学习
1.共线向量定理:两个空间向量、(≠),//的充要条件是存在唯一的实数x,使 。
思考一:(1)≠的原因 。
(2)用共线向量定理证明两直线平行应注意什么问题?
2.共面向量:
已知向量,作,如果的基线 ,则就说向量平行于平面,记作: 。通常我们把平行于同一平面的向量,叫做 。
思考二:(1),的基线一定与平面平行吗?
合作探究
共面向量定理:如果两个向量不共线,与向量共面的充要条件是存在唯一的一对实数使 。
思考三:(1)这个定理的条件和结论分别是什么?
(2)证明其必要性是由谁推出谁?证明其充分性是由谁推出谁?
证明:
思考四:1.若,能不能说明所在的基线都共面?
2.平行向量基本定理与共面向量定理有什么区别?
知识运用
例1.已知斜三棱柱ABC-A/B/C/(如图),设。在面对角线AC/上和棱BC上分别取点M和N,使求证:与向量 和共面。
引申:条件不变,结论变为MN//平面AA/B/B.
例2.对空间任一点O和不共线的三点A,B,C,问满足向量式(其中x + y + z=1)的四点是否共面?
跟踪练习:已知三点不共线,对平面外任一点,满足,试判断:点与是否一定共面?
【达标检测】
已知平行四边形ABCD,从平面外一点引向量,求证:四点E、F、G、H共面;
问题:在平面上,任一向量都能用两个不共线的向量来表示,若空间三个向量不共面,那么空间的任一向量能不能用这三个向量表示。同学们类比平面向量基本定理,
猜想结论:
预习:空间向量分解定理的证明与应用。
1.下列说法正确的是( )
A.与非零向量共线,与共线,则与共线
B. 任意两个相等向量不一定共线
C. 任意两个共线向量相等
D. 若向量与共线,则
2.对于空间中的三个向量,它们一定是:( )
A.共面向量 B.共线向量 C.不共面向量 D.既不共线又不共面向量
3.已知三点不共线,对平面外任一点,满足条件,
试判断:点与是否一定共面?
4.
B
4 / 4
