数学高中苏教版选修(2-2)1.3《导数在研究函数中的应用》课件2
文档属性
| 名称 | 数学高中苏教版选修(2-2)1.3《导数在研究函数中的应用》课件2 |

|
|
| 格式 | zip | ||
| 文件大小 | 243.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-04 00:00:00 | ||
图片预览




文档简介
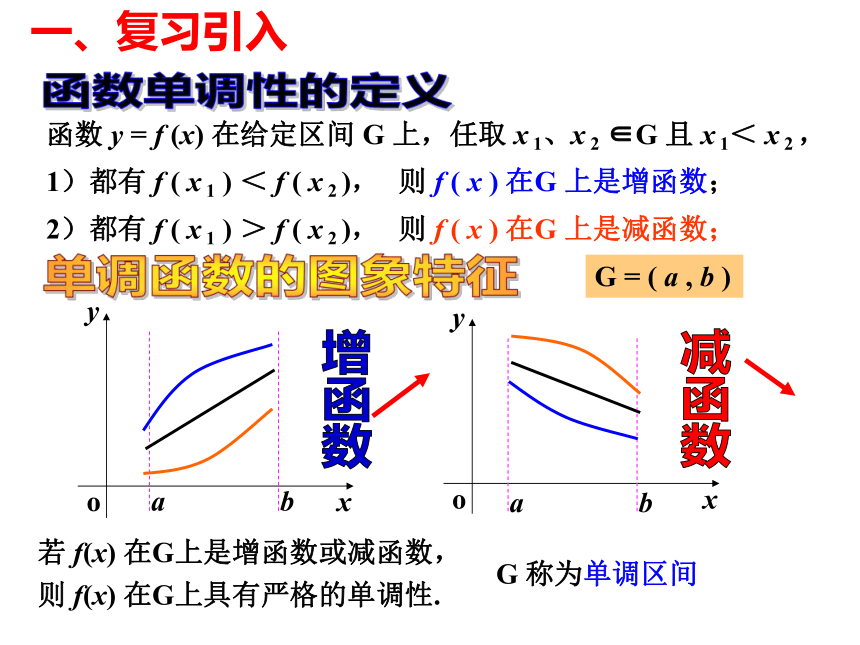
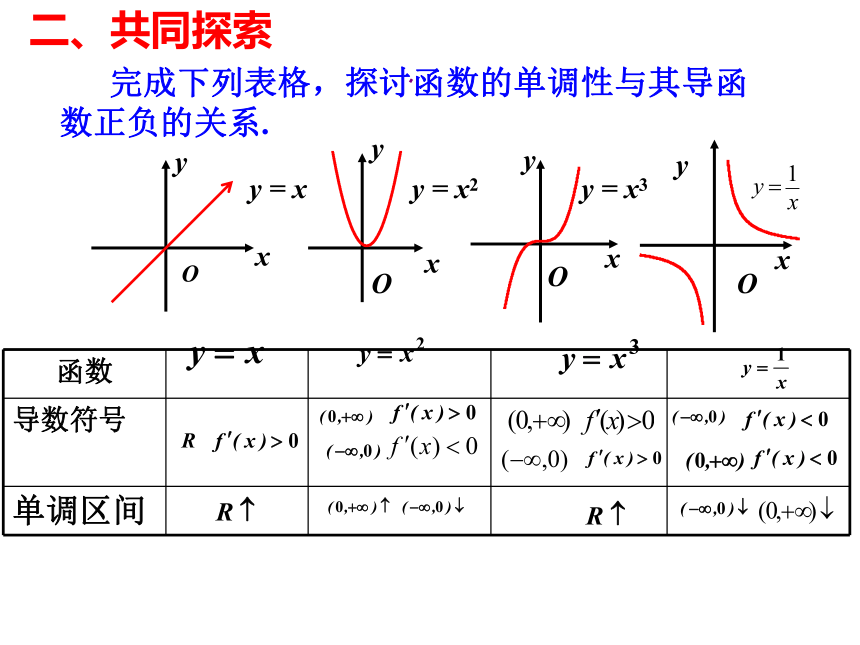
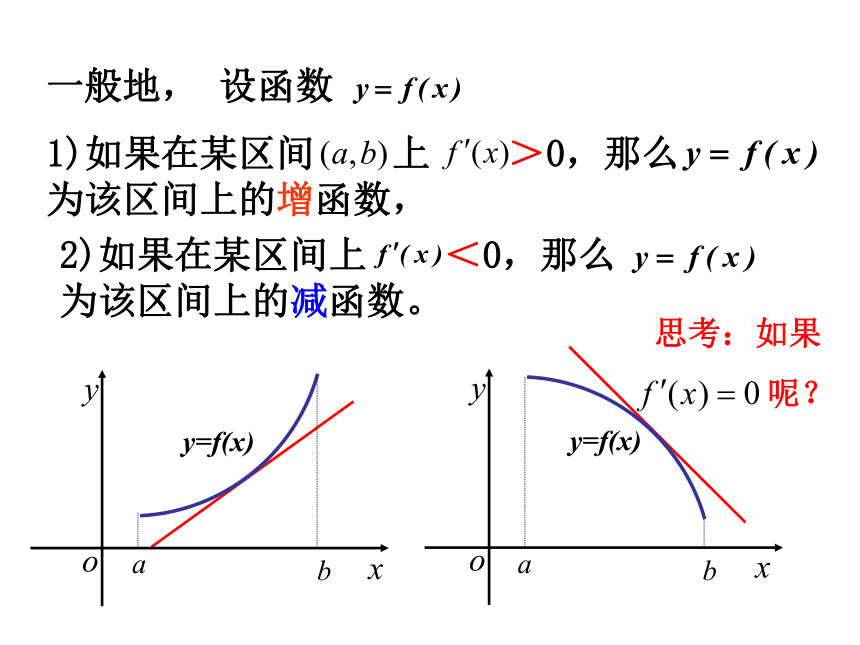
课件19张PPT。4、对数函数的导数:5、指数函数的导数:3、三角函数 : 1、常函数:(C)′? (c为常数); 2、幂函数 : (xn)′? 课 前 热 身6、求下列函数的导数:函数的单调性与导数高二数学选修2-2第一章- -导数及其应用之函数 y = f (x) 在给定区间 G 上,任取 x 1、x 2 ∈G 且 x 1< x 2 ,函数单调性的定义单调函数的图象特征1)都有 f ( x 1 ) < f ( x 2 ),则 f ( x ) 在G 上是增函数;2)都有 f ( x 1 ) > f ( x 2 ),则 f ( x ) 在G 上是减函数;若 f(x) 在G上是增函数或减函数,增函数减函数则 f(x) 在G上具有严格的单调性.G 称为单调区间G = ( a , b ) 一、复习引入 二、共同探索 完成下列表格,探讨函数的单调性与其导函数正负的关系.yyxyOy = xxxOOy = x3xyOy = x2一般地, 设函数1)如果在某区间 上 >0,那么 为该区间上的增函数,2)如果在某区间上 <0,那么 为该区间上的减函数。思考:如果
呢?例1、已知导函数f′(x)的下列信息:当10;当x>4,或x<1时,f′(x)<0当x=4,或x=1时, f′(x)=0试画出函数f(x)图像的大致形状三、导数的应用:设 是函数 的导函数, 的图象如
右图所示,则 的图象最有可能的是( )C变式例2、判断下列函数的单调性,并求出单调区间:课堂练习:共同完成课本25页填空,时间3分钟解:函数的定义域是(-1,+∞),深入研究由 即 得x<-1或x>1.因为函数的定义域是(-1,+∞),故f(x)的递增区间是(1,+∞);由 解得-1在某个区间 如果函数 是单课后思考(或 )吗?调递增的(或单调递减的),那么 3、 利用导数讨论函数的单调性1、函数的单调性与导数的关系.(一定要先确定函数的定义域,解决问题的过程中,只能在函数的定义域内)2、能根据导函数的特别绘制大致函数图象.四、课堂小结(谈谈你的收获) 今日作业:
课本P31 习题1.3 1、2 做在作业本上四、综合应用:例1:确定下列函数的单调区间:
(1)f(x)=x/2+sinx;解:(1)函数的定义域是R,令 ,解得令 ,解得因此,f(x)的递增区间是:
递减区间是:例2:设f(x)=ax3+x恰有三个单调区间,试确定a的取值 范 围,并求其单调区间.解:若a>0, 对一切实数恒成立,此时f(x)只有一
个单调区间,矛盾.若a=0, 此时f(x)也只有一个单调区间,矛盾. 若a<0,则 ,易知此时f(x)
恰有三个单调区间.故a<0,其单调区间是:单调递增区间:单调递减区间: 和
呢?例1、已知导函数f′(x)的下列信息:当1
右图所示,则 的图象最有可能的是( )C变式例2、判断下列函数的单调性,并求出单调区间:课堂练习:共同完成课本25页填空,时间3分钟解:函数的定义域是(-1,+∞),深入研究由 即 得x<-1或x>1.因为函数的定义域是(-1,+∞),故f(x)的递增区间是(1,+∞);由 解得-1
课本P31 习题1.3 1、2 做在作业本上四、综合应用:例1:确定下列函数的单调区间:
(1)f(x)=x/2+sinx;解:(1)函数的定义域是R,令 ,解得令 ,解得因此,f(x)的递增区间是:
递减区间是:例2:设f(x)=ax3+x恰有三个单调区间,试确定a的取值 范 围,并求其单调区间.解:若a>0, 对一切实数恒成立,此时f(x)只有一
个单调区间,矛盾.若a=0, 此时f(x)也只有一个单调区间,矛盾. 若a<0,则 ,易知此时f(x)
恰有三个单调区间.故a<0,其单调区间是:单调递增区间:单调递减区间: 和
