数学高中苏教版选修(2-2)1.3《导数在研究函数中的应用》课件4
文档属性
| 名称 | 数学高中苏教版选修(2-2)1.3《导数在研究函数中的应用》课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 220.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-04 21:08:24 | ||
图片预览











文档简介
课件50张PPT。1.3. 导数的应用理解函数的最大值、最小值的概念;了解函数的极值与最值的区别与联系;会用导数求在给定区间上不超过三次的多项式函数的最大值、最小值.体会导数方法在研究函数性质中的一般性和有效性.1.函数f(x)在闭区间[a,b]上的最值
如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,则该函数在[a,b]上一定能够取得①________和②________并且函数的最值必在③________或④________取得.
2.求函数y=f(x)在[a,b]上最值的步骤
(1)求函数y=f(x)⑤________;
(2)将函数y=f(x)的⑥________与⑦________比较,其中最大的一个是最大值,最小的一个是最小值:自我校对:①最大值 ②最小值 ③极值点处 ④端点处 ⑤在[a,b]内的极值 ⑥各极值 ⑦端点处的函数值f(a),f(b)
1.下列说法正确的是 ( )
A.函数在其定义域内若有最值与极值,则其极大值便是最大值,极小值便是最小值
B.闭区间上的连续函数一定有最值,也一定有极值
C.若函数在其定义域上有最值,则一定有极值;反之,若有极值则一定有最值
D.若函数在给定区间上有最值,则最多有一个最大值,一个最小值,但若有极值,则可有多个极值解析:最值与极值概念.故选D.
答案:D*2.函数y=|x-1|,下列结论正确的是( )
A.y有极小值0,且0也是最小值
B.y有最小值0,但0不是极小值
C.y有极小值0,但0不是最小值
D.因为y在x=1处不可导,所以0既非最小值也非极值
解析:最小值与极小值定义的应用.故选A.
答案:A*答案:B练习4-5答案:2,-25.求函数f(x)=x3-3x2+6x-2在区间[-1,1]上的最值.
解析:f′(x)=3x2-6x+6=3(x2-2x+2),
因为f′(x)在[-1,1]内恒大于0,所以f(x)在[-1,1]上是增函数,
故当x=-1时,f(x)取得最小值-12;当x=1时,f(x)取得最大值2.
即f(x)的最大值为2,最小值为-12.
1.函数f(x)的图象在区间[a,b]上连续不断是f(x)在[a,b]上存在最大值和最小值的充分而非必要条件.
2.当f(x)的图象连续不断且在[a,b]上单调时,其最大值、最小值在端点处取得.
3.当图象连续不断的函数f(x)在(a,b)内只有一个可疑点时,若在这一点处f(x)有极大(或极小)值,则可以断定f(x)在该点处取到最大(或最小)值,这里(a,b)也可以是无穷区间.4.函数的极值可以有多个,但最大(小)值只能有一个,极值只能在区间内取得,最值可以在端点处取得;有极值的未必有最值,有最值的未必有极值,极值有可能成为最值,最值只要不在端点处,则必为极值.
5.函数f(x)在区间(a,b)上的最值
在区间(a,b)上函数f(x)的图象是一条连续的曲线时,f(x)在(a,b)内不一定有最值.常见的有以下几种情况:
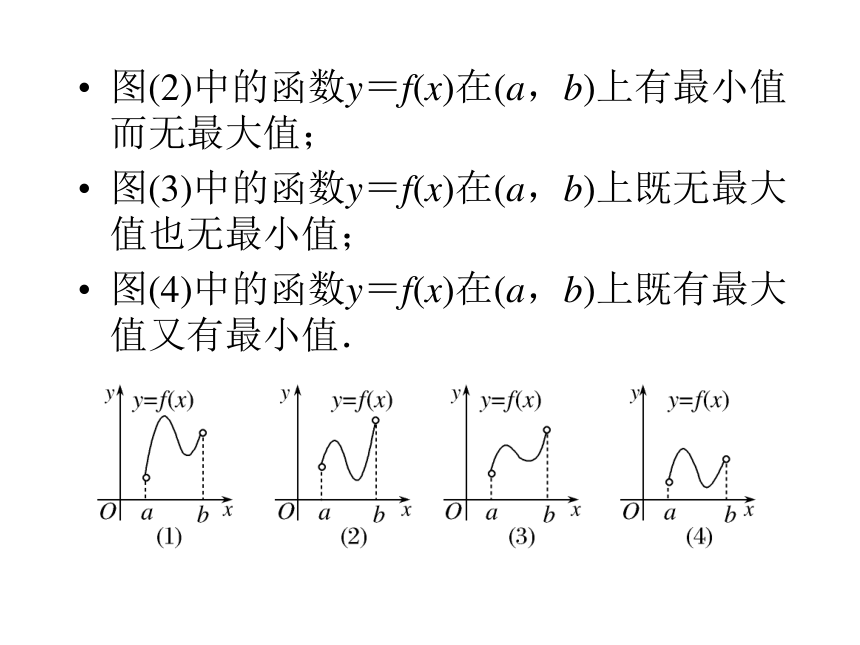
如图,图(1)中的函数y=f(x)在(a,b)上有最大值而无最小值; 图(2)中的函数y=f(x)在(a,b)上有最小值而无最大值;
图(3)中的函数y=f(x)在(a,b)上既无最大值也无最小值;
图(4)中的函数y=f(x)在(a,b)上既有最大值又有最小值.
[分析] 求函数在闭区间[a,b]上的最值.应先求极值,再求区间端点值,然后比较极值与端点值,从而找出最大值和最小值.∴当x=0时,f(x)有最小值f(0)=0;
当x=2π,f(x)有最大值f(2π)=π.
当x∈[0,a]时,f′(x)<0恒成立,
即f(x)在[0,a]上是减函数.
故当x=a时,f(x)有最小值f(a)=e-a-ea;当x=0时,f(x)有最大值f(0)=e-0-e0=0.
[点拨] (1)用导数求函数的最值和求函数的极值方法类似,在给定区间是闭区间时,极值要和区间端点的函数值进行比较,并且要注意极值点是否在区间内.
(2)当函数多项式的次数大于2或用传统方法不易求最值时,可考虑用导数的方法求解.练 1 求下列函数在给定区间上的最大值与最小值.
(1)f(x)=2x3-3x2-12x+5,x∈[-2,3];
(2)f(x)=x3-3x2+6x-2,x∈[-1,1];[解] (1)f′(x)=6x2-6x-12,
令f′(x)=0,则6x2-6x-12=0,即x2-x-2=0,
解得x1=-1,x2=2.
∵f(-1)=12,f(2)=-15,f(-2)=1,f(3)=-4,
∴函数f(x)=2x3-3x2-12x+5在x∈[-2,3]上的最大值为12,最小值为-15.
(2)f′(x)=3x2-6x+6=3(x2-2x+2),
∵f′(x)在[-1,1]内恒大于0,
∴f(x)在[-1,1]上单调递增.∴f(x)=x3-3x2+6x-2在[-1,1]上的最大值为f(1)=2,最小值为f(-1)=-12.
(3)f′(x)=2cos2x-1,
已解例2:
已知函数f(x)=ax3-6ax2+b,问是否存在实数a、b,使f(x)在[-1,2]上取得最大值3,最小值-29?若存在,求出a,b的值;若不存在,请说明理由.
[分析] 函数最值的逆向问题,通常是已知函数的最值求函数关系式中字母的值的问题.解决时应利用函数的极值与最值相比较,综合运用求极值、最值的方法确定系数的方程(组),解之即可.[解] 显然a≠0.
f′(x)=3ax2-12ax=3ax(x-4).
令f′(x)=0,解得x1=0,x2=4(舍去).
(1)当a>0时,当x变化时,f′(x),f(x)的变化情况如下表:所以当x=0时,f(x)取得最大值,所以f(0)=b=3.
又f(2)=-16a+3,f(-1)=-7a+3,f(-1)>f(2).
所以当x=2时,f(x)取得最小值,即-16a+3=-29,a=2.
(2)当a<0时,当x变化时,f′(x),f(x)的变化情况如下表:所以当x=0时,f(x)取得最小值,所以b=-29.
又f(2)=-16a-29,f(-1)=-7a-29,f(2)>f(-1).
所以当x=2时,f(x)取得最大值,即-16a-29=3,a=-2.
综上所述a=2,b=3或a=-2,b=-29.
[点拨] 本题运用了求极值、最值的方法,采用了待定系数法确定a,b的值,体现了方程的思想和分类讨论的思想.练 2: 已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为 ( )
A.-37 B.-29
C.-5 D.-11
[解析] 由f′(x)=6x2-12x=6x(x-2)=0,解得x=0或x=2,f(0)=m,f(2)=m-8,f(-2)=m-40,所以f(x)max=m=3,f(x)min=m-40=3-40=-37.
[答案] A 思?[分析] 在函数、不等式的交汇点处命题,将不等式恒成立问题,转化为利用导数求函数最值的问题.
即证明x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
令g(x)=(x+1)ln(x+1)+1-2x,
则g′(x)=ln(x+1)-1.
当x>e-1时g′(x)>0;当0∴当x=e-1时,g(x)取得最小值g(e-1)=3-e>0.∴当x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
因此正整数k的最大值为3.
*[点拨] 解决含参不等式在给定区间上恒成立问题的一般方法是分离参数法.若f(x)>m恒成立?f(x)min>m,若f(x)(1)求a、b的值及函数f(x)的单调递增区间;
(2)若对x∈[-1,2],不等式f(x)故要使f(x)只需k2>f(2),即k2>2+k,解得k<-1或k>2.
∴k的取值范围是(-∞,-1)∪(2,+∞).
删例4: 动点P(x,y)是抛物线y=x2-2x-1上的点,O为原点,设S=|OP|2,求S的最小值.
[分析] 以函数、不等式、解析几何、立体几何等知识为载体,求某些具体问题的最值.[解析] S=|OP|2=x2+y2=x2+(x2-2x-1)2
=x4-4x3+3x2+4x+1,
S′=4x3-12x2+6x+4=2(x-2)(2x2-2x-1)[点拨] 解析几何中求最值问题,是高考常考问题,利用导数法求最值,为突破解析几何的难点,提供了便捷的工具,体现了导数法研究函数的优越性.练 4: (2009·重庆)已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(2)若当x=-1时,函数y=g(x)取得极值,确定y=g(x)的单调区间.[解] (1)因f(x)=x2+bx+c为偶函数,故f(-x)=f(x).
即(-x)2+b(-x)+c=x2+bx+c,从而b=-b,解b=0.
又函数y=f(x)过点(2,5),得4+c=5,c=1,
g(x)=(x+a)(x2+1)=x3+ax2+x+a,
从而g′(x)=3x2+2ax+1.
因曲线y=g(x)有斜率为0的切线,故g′(x)=0有实数解,
(2)因函数g(x)在x=-1处取得极值,故g′(-1)=0.
即3-2a+1=0,解得a=2.
又g′(x)=3x2+4x+1=(3x+1)(x+1),
(1)讨论f(x)的单调性;
(2)若当x≥0时,f(x)>0恒成立,求a的取值范围.[分析] 本题考查导数与函数的综合运用能力,涉及利用导数讨论函数的单调性,第一问关键是通过分析导函数,从而确定函数的单调性,第二问是利用导数及函数的最值,由恒成立条件得出不等式条件从而求出a的取值范围.
[解] (1)f′(x)=x2-2(1+a)x+4a
=(x-2)(x-2a).
当a>1知,当x<2时,f′(x)>0,
故f(x)在区间(-∞,2)是增函数.
当2故f(x)在区间(2,2a)是减函数;
当x>2a时,f′(x)>0,
故f(x)在区间(2a,+∞)是增函数.
综上,当a>1时,f(x)在区间(-∞,2)和(2a,+∞)上是增函数,在区间(2,2a)上是减函数.(2)由(1)知,当x≥0时,f(x)在x=2a或x=0处取得最小值.
如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,则该函数在[a,b]上一定能够取得①________和②________并且函数的最值必在③________或④________取得.
2.求函数y=f(x)在[a,b]上最值的步骤
(1)求函数y=f(x)⑤________;
(2)将函数y=f(x)的⑥________与⑦________比较,其中最大的一个是最大值,最小的一个是最小值:自我校对:①最大值 ②最小值 ③极值点处 ④端点处 ⑤在[a,b]内的极值 ⑥各极值 ⑦端点处的函数值f(a),f(b)
1.下列说法正确的是 ( )
A.函数在其定义域内若有最值与极值,则其极大值便是最大值,极小值便是最小值
B.闭区间上的连续函数一定有最值,也一定有极值
C.若函数在其定义域上有最值,则一定有极值;反之,若有极值则一定有最值
D.若函数在给定区间上有最值,则最多有一个最大值,一个最小值,但若有极值,则可有多个极值解析:最值与极值概念.故选D.
答案:D*2.函数y=|x-1|,下列结论正确的是( )
A.y有极小值0,且0也是最小值
B.y有最小值0,但0不是极小值
C.y有极小值0,但0不是最小值
D.因为y在x=1处不可导,所以0既非最小值也非极值
解析:最小值与极小值定义的应用.故选A.
答案:A*答案:B练习4-5答案:2,-25.求函数f(x)=x3-3x2+6x-2在区间[-1,1]上的最值.
解析:f′(x)=3x2-6x+6=3(x2-2x+2),
因为f′(x)在[-1,1]内恒大于0,所以f(x)在[-1,1]上是增函数,
故当x=-1时,f(x)取得最小值-12;当x=1时,f(x)取得最大值2.
即f(x)的最大值为2,最小值为-12.
1.函数f(x)的图象在区间[a,b]上连续不断是f(x)在[a,b]上存在最大值和最小值的充分而非必要条件.
2.当f(x)的图象连续不断且在[a,b]上单调时,其最大值、最小值在端点处取得.
3.当图象连续不断的函数f(x)在(a,b)内只有一个可疑点时,若在这一点处f(x)有极大(或极小)值,则可以断定f(x)在该点处取到最大(或最小)值,这里(a,b)也可以是无穷区间.4.函数的极值可以有多个,但最大(小)值只能有一个,极值只能在区间内取得,最值可以在端点处取得;有极值的未必有最值,有最值的未必有极值,极值有可能成为最值,最值只要不在端点处,则必为极值.
5.函数f(x)在区间(a,b)上的最值
在区间(a,b)上函数f(x)的图象是一条连续的曲线时,f(x)在(a,b)内不一定有最值.常见的有以下几种情况:
如图,图(1)中的函数y=f(x)在(a,b)上有最大值而无最小值; 图(2)中的函数y=f(x)在(a,b)上有最小值而无最大值;
图(3)中的函数y=f(x)在(a,b)上既无最大值也无最小值;
图(4)中的函数y=f(x)在(a,b)上既有最大值又有最小值.
[分析] 求函数在闭区间[a,b]上的最值.应先求极值,再求区间端点值,然后比较极值与端点值,从而找出最大值和最小值.∴当x=0时,f(x)有最小值f(0)=0;
当x=2π,f(x)有最大值f(2π)=π.
当x∈[0,a]时,f′(x)<0恒成立,
即f(x)在[0,a]上是减函数.
故当x=a时,f(x)有最小值f(a)=e-a-ea;当x=0时,f(x)有最大值f(0)=e-0-e0=0.
[点拨] (1)用导数求函数的最值和求函数的极值方法类似,在给定区间是闭区间时,极值要和区间端点的函数值进行比较,并且要注意极值点是否在区间内.
(2)当函数多项式的次数大于2或用传统方法不易求最值时,可考虑用导数的方法求解.练 1 求下列函数在给定区间上的最大值与最小值.
(1)f(x)=2x3-3x2-12x+5,x∈[-2,3];
(2)f(x)=x3-3x2+6x-2,x∈[-1,1];[解] (1)f′(x)=6x2-6x-12,
令f′(x)=0,则6x2-6x-12=0,即x2-x-2=0,
解得x1=-1,x2=2.
∵f(-1)=12,f(2)=-15,f(-2)=1,f(3)=-4,
∴函数f(x)=2x3-3x2-12x+5在x∈[-2,3]上的最大值为12,最小值为-15.
(2)f′(x)=3x2-6x+6=3(x2-2x+2),
∵f′(x)在[-1,1]内恒大于0,
∴f(x)在[-1,1]上单调递增.∴f(x)=x3-3x2+6x-2在[-1,1]上的最大值为f(1)=2,最小值为f(-1)=-12.
(3)f′(x)=2cos2x-1,
已解例2:
已知函数f(x)=ax3-6ax2+b,问是否存在实数a、b,使f(x)在[-1,2]上取得最大值3,最小值-29?若存在,求出a,b的值;若不存在,请说明理由.
[分析] 函数最值的逆向问题,通常是已知函数的最值求函数关系式中字母的值的问题.解决时应利用函数的极值与最值相比较,综合运用求极值、最值的方法确定系数的方程(组),解之即可.[解] 显然a≠0.
f′(x)=3ax2-12ax=3ax(x-4).
令f′(x)=0,解得x1=0,x2=4(舍去).
(1)当a>0时,当x变化时,f′(x),f(x)的变化情况如下表:所以当x=0时,f(x)取得最大值,所以f(0)=b=3.
又f(2)=-16a+3,f(-1)=-7a+3,f(-1)>f(2).
所以当x=2时,f(x)取得最小值,即-16a+3=-29,a=2.
(2)当a<0时,当x变化时,f′(x),f(x)的变化情况如下表:所以当x=0时,f(x)取得最小值,所以b=-29.
又f(2)=-16a-29,f(-1)=-7a-29,f(2)>f(-1).
所以当x=2时,f(x)取得最大值,即-16a-29=3,a=-2.
综上所述a=2,b=3或a=-2,b=-29.
[点拨] 本题运用了求极值、最值的方法,采用了待定系数法确定a,b的值,体现了方程的思想和分类讨论的思想.练 2: 已知f(x)=2x3-6x2+m(m为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值为 ( )
A.-37 B.-29
C.-5 D.-11
[解析] 由f′(x)=6x2-12x=6x(x-2)=0,解得x=0或x=2,f(0)=m,f(2)=m-8,f(-2)=m-40,所以f(x)max=m=3,f(x)min=m-40=3-40=-37.
[答案] A 思?[分析] 在函数、不等式的交汇点处命题,将不等式恒成立问题,转化为利用导数求函数最值的问题.
即证明x>0时,(x+1)ln(x+1)+1-2x>0恒成立.
令g(x)=(x+1)ln(x+1)+1-2x,
则g′(x)=ln(x+1)-1.
当x>e-1时g′(x)>0;当0
因此正整数k的最大值为3.
*[点拨] 解决含参不等式在给定区间上恒成立问题的一般方法是分离参数法.若f(x)>m恒成立?f(x)min>m,若f(x)
(2)若对x∈[-1,2],不等式f(x)
∴k的取值范围是(-∞,-1)∪(2,+∞).
删例4: 动点P(x,y)是抛物线y=x2-2x-1上的点,O为原点,设S=|OP|2,求S的最小值.
[分析] 以函数、不等式、解析几何、立体几何等知识为载体,求某些具体问题的最值.[解析] S=|OP|2=x2+y2=x2+(x2-2x-1)2
=x4-4x3+3x2+4x+1,
S′=4x3-12x2+6x+4=2(x-2)(2x2-2x-1)[点拨] 解析几何中求最值问题,是高考常考问题,利用导数法求最值,为突破解析几何的难点,提供了便捷的工具,体现了导数法研究函数的优越性.练 4: (2009·重庆)已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)若曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(2)若当x=-1时,函数y=g(x)取得极值,确定y=g(x)的单调区间.[解] (1)因f(x)=x2+bx+c为偶函数,故f(-x)=f(x).
即(-x)2+b(-x)+c=x2+bx+c,从而b=-b,解b=0.
又函数y=f(x)过点(2,5),得4+c=5,c=1,
g(x)=(x+a)(x2+1)=x3+ax2+x+a,
从而g′(x)=3x2+2ax+1.
因曲线y=g(x)有斜率为0的切线,故g′(x)=0有实数解,
(2)因函数g(x)在x=-1处取得极值,故g′(-1)=0.
即3-2a+1=0,解得a=2.
又g′(x)=3x2+4x+1=(3x+1)(x+1),
(1)讨论f(x)的单调性;
(2)若当x≥0时,f(x)>0恒成立,求a的取值范围.[分析] 本题考查导数与函数的综合运用能力,涉及利用导数讨论函数的单调性,第一问关键是通过分析导函数,从而确定函数的单调性,第二问是利用导数及函数的最值,由恒成立条件得出不等式条件从而求出a的取值范围.
[解] (1)f′(x)=x2-2(1+a)x+4a
=(x-2)(x-2a).
当a>1知,当x<2时,f′(x)>0,
故f(x)在区间(-∞,2)是增函数.
当2
当x>2a时,f′(x)>0,
故f(x)在区间(2a,+∞)是增函数.
综上,当a>1时,f(x)在区间(-∞,2)和(2a,+∞)上是增函数,在区间(2,2a)上是减函数.(2)由(1)知,当x≥0时,f(x)在x=2a或x=0处取得最小值.
