数学高中苏教版选修(2-2)1.3《导数在研究函数中的应用》课件
文档属性
| 名称 | 数学高中苏教版选修(2-2)1.3《导数在研究函数中的应用》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 381.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-04 21:04:17 | ||
图片预览








文档简介
课件24张PPT。1.3导数在研究函数中的应用(3)用函数的导数为0的点,顺次将函数的定义区间分成若干小开区间,并列成表格.检查f′(x)在方程根左右的值的符号,求出极大值和极小值.二、 求函数f(x)的极值的步骤:(1)求导数f′(x);(2)求方程f′(x)=0的根(x为极值点.)练习:求函数 的极值x=-2时,y有极大值-8,
当x=2时,y有极小值8练习:
如果函数 f(x)=ax5-bx3+c(a≠0)在x=±1时有极值,极大值为4,极小值为0 ,试求a,b,c的值 .练习:
如果函数 f(x)=ax5-bx3+c(a≠0)在x=±1时有极值,极大值为4,极小值为0 ,试求a,b,c的值 . 0+极大无极值练习:
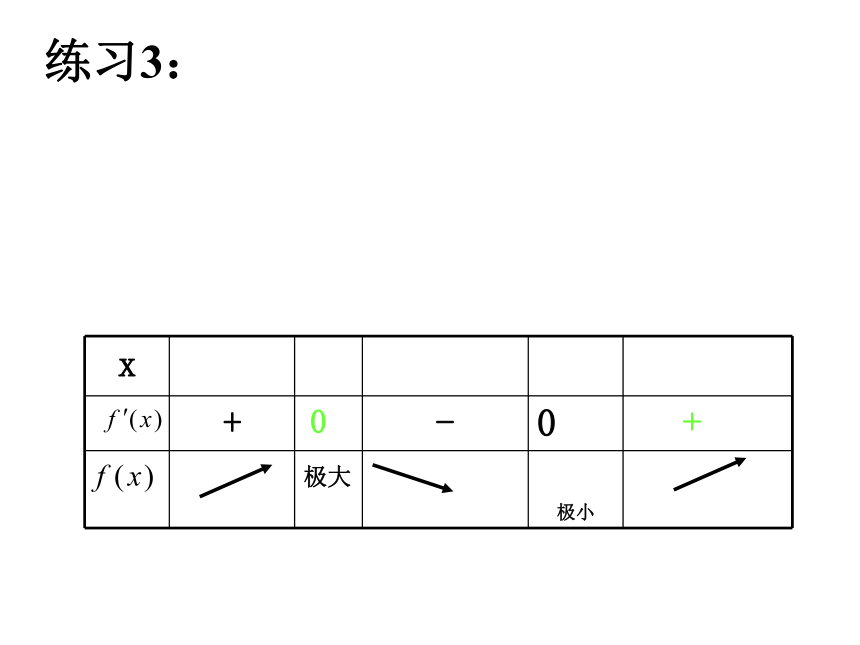
如果函数 f(x)=ax5-bx3+c(a≠0)在x=±1时有极值,极大值为4,极小值为0 ,试求a,b,c的值 . 练习3:0+极大0+极大1.已知函数f(x)=x3-3ax2+2bx在点x=1处有极小值-1,试确定a,b的值,并求出f(x)的单调区间。作业:2.三次函数f(x)=x3+ax2+x在区间[-1,1]
上有极大值和极小值,求常数a的取值
范围.1.3.3 最大值与最小值一.最值的概念(最大值与最小值)新 课 讲 授 如果在函数定义域I内存在x0,使得对任意的x∈I,总有f(x) ≤f(x0),
则称f(x0)为函数f(x)在定义域上的
最大值.最值是相对函数定义域整体而言的.1.在定义域内, 最值唯一;极值不唯一;注意:2.最大值一定比最小值大.观察下面函数 y = f (x) 在区间 [ a , b ] 上的图象, 回答:(1) 在哪一点处函数 y = f (x) 有极大值和极小值?(2) 函数 y = f (x) 在[a,b]上有最大值和最小值吗?如果有,
最大值和最小值分别是什么?x1x2x3x4x5极大:x = x1x = x2x = x3x = x5极小:x = x4观察下面函数 y = f (x) 在区间 [ a , b ] 上的图象, 回答:(1) 在哪一点处函数 y = f (x) 有极大值和极小值?(2) 函数 y = f (x) 在[a,b]上有最大值和最小值吗?如果有,
最大值和最小值分别是什么?极大:x = x1x = x2x = x3极小:abxyx1Ox2x3二.如何求函数的最值?(1)利用函数的单调性;(2)利用函数的图象;(3)利用函数的导数;如:求y=2x+1在区间[1,3]上的最值.如:求y=(x-2)2+3在区间[1,3]上的最值.求函数 y = f (x) 在[a,b]上的最大值与最小值的步骤如下:(1) 求函数 y = f (x) 在 ( a, b ) 内的极值;(2) 将函数 y = f (x) 的各极值点与端点处的函数值f (a), f (b) 比较, 其中最大的一个是最大值, 最小的一个是最小值. 例1、求函数f(x)=x2-4x+6在区间[1,5]内的最大值和最小值 解:f ′(x)=2x- 4令f′(x)=0,即2x–4=0,得x =2-+3112 故函数f (x) 在区间[1,5]内的最大值为11,最小值为2 若函数f(x)在所给的区间I内有唯一的极值,则它是函数的
最值例2 求函数 在[0,3]上的最大值与最小值.解: 令解得 x = 2 .所以当 x = 2 时, 函数 f (x)有极小值又由于所以, 函数 在[0,3]上的最大值是4,最小值是 当0≤x<2时,f’(x)<0;当20 函数 ,在[-1,1]上的最小值为( )
A.0 B.-2 C.-1 D.13/12A练 习2、函数 ( ) A.有最大值2,无最小值
B.无最大值,有最小值-2
C.最大值为2,最小值-2
D.无最值3、函数 A.是增函数 B.是减函数
C.有最大值 D.最小值C例3、解:已知三次函数f(x)=ax3-6ax2+b.问是否存在实数a,b,使f(x)在[-1,2]上取得最大值3,最小值-29,若存在,求出a,b的值;若不存在,请说明理由。已知三次函数f(x)=ax3-6ax2+b.问是否存在实数a,b,使f(x)在[-1,2]上取得最大值3,最小值-29,若存在,求出a,b的值;若不存在,请说明理由。
当x=2时,y有极小值8练习:
如果函数 f(x)=ax5-bx3+c(a≠0)在x=±1时有极值,极大值为4,极小值为0 ,试求a,b,c的值 .练习:
如果函数 f(x)=ax5-bx3+c(a≠0)在x=±1时有极值,极大值为4,极小值为0 ,试求a,b,c的值 . 0+极大无极值练习:
如果函数 f(x)=ax5-bx3+c(a≠0)在x=±1时有极值,极大值为4,极小值为0 ,试求a,b,c的值 . 练习3:0+极大0+极大1.已知函数f(x)=x3-3ax2+2bx在点x=1处有极小值-1,试确定a,b的值,并求出f(x)的单调区间。作业:2.三次函数f(x)=x3+ax2+x在区间[-1,1]
上有极大值和极小值,求常数a的取值
范围.1.3.3 最大值与最小值一.最值的概念(最大值与最小值)新 课 讲 授 如果在函数定义域I内存在x0,使得对任意的x∈I,总有f(x) ≤f(x0),
则称f(x0)为函数f(x)在定义域上的
最大值.最值是相对函数定义域整体而言的.1.在定义域内, 最值唯一;极值不唯一;注意:2.最大值一定比最小值大.观察下面函数 y = f (x) 在区间 [ a , b ] 上的图象, 回答:(1) 在哪一点处函数 y = f (x) 有极大值和极小值?(2) 函数 y = f (x) 在[a,b]上有最大值和最小值吗?如果有,
最大值和最小值分别是什么?x1x2x3x4x5极大:x = x1x = x2x = x3x = x5极小:x = x4观察下面函数 y = f (x) 在区间 [ a , b ] 上的图象, 回答:(1) 在哪一点处函数 y = f (x) 有极大值和极小值?(2) 函数 y = f (x) 在[a,b]上有最大值和最小值吗?如果有,
最大值和最小值分别是什么?极大:x = x1x = x2x = x3极小:abxyx1Ox2x3二.如何求函数的最值?(1)利用函数的单调性;(2)利用函数的图象;(3)利用函数的导数;如:求y=2x+1在区间[1,3]上的最值.如:求y=(x-2)2+3在区间[1,3]上的最值.求函数 y = f (x) 在[a,b]上的最大值与最小值的步骤如下:(1) 求函数 y = f (x) 在 ( a, b ) 内的极值;(2) 将函数 y = f (x) 的各极值点与端点处的函数值f (a), f (b) 比较, 其中最大的一个是最大值, 最小的一个是最小值. 例1、求函数f(x)=x2-4x+6在区间[1,5]内的最大值和最小值 解:f ′(x)=2x- 4令f′(x)=0,即2x–4=0,得x =2-+3112 故函数f (x) 在区间[1,5]内的最大值为11,最小值为2 若函数f(x)在所给的区间I内有唯一的极值,则它是函数的
最值例2 求函数 在[0,3]上的最大值与最小值.解: 令解得 x = 2 .所以当 x = 2 时, 函数 f (x)有极小值又由于所以, 函数 在[0,3]上的最大值是4,最小值是 当0≤x<2时,f’(x)<0;当2
A.0 B.-2 C.-1 D.13/12A练 习2、函数 ( ) A.有最大值2,无最小值
B.无最大值,有最小值-2
C.最大值为2,最小值-2
D.无最值3、函数 A.是增函数 B.是减函数
C.有最大值 D.最小值C例3、解:已知三次函数f(x)=ax3-6ax2+b.问是否存在实数a,b,使f(x)在[-1,2]上取得最大值3,最小值-29,若存在,求出a,b的值;若不存在,请说明理由。已知三次函数f(x)=ax3-6ax2+b.问是否存在实数a,b,使f(x)在[-1,2]上取得最大值3,最小值-29,若存在,求出a,b的值;若不存在,请说明理由。
