数学高中苏教版选修(2-1)3.1《空间向量及其运算》复习课件
文档属性
| 名称 | 数学高中苏教版选修(2-1)3.1《空间向量及其运算》复习课件 |  | |
| 格式 | zip | ||
| 文件大小 | 922.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-04 21:06:46 | ||
图片预览










文档简介
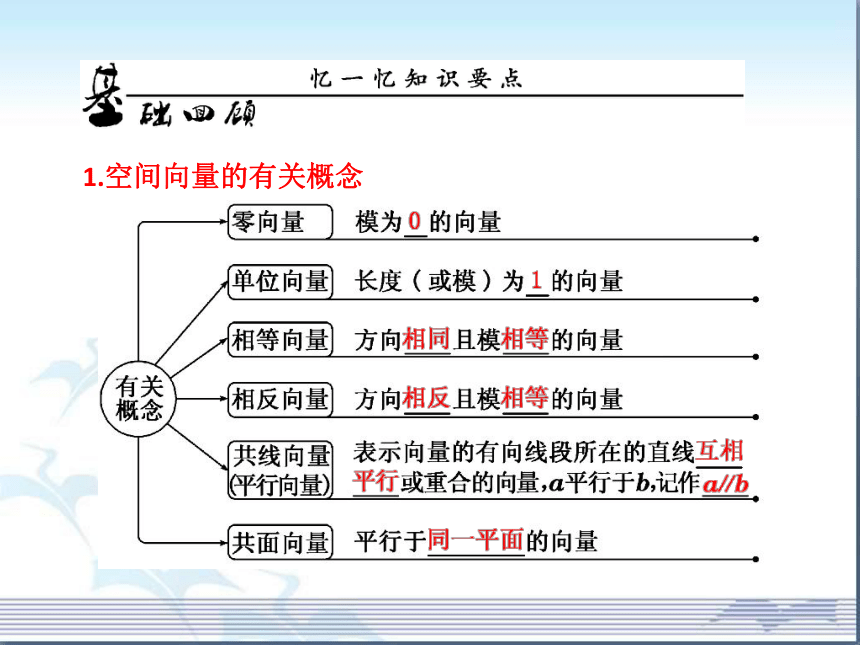
课件34张PPT。1.空间向量的有关概念
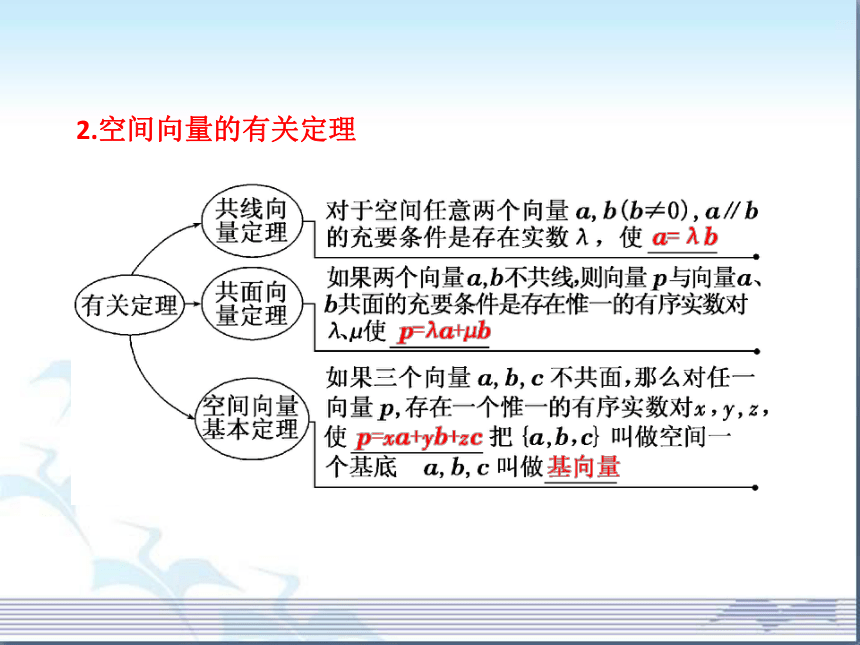
2.空间向量的有关定理
[思考探究]
若a与b确定平面为α,则表示a的有向线段与α的关系是怎样的?
提示:可能与α平行,也可能在α内.3.空间向量的数量积及运算律
4.空间向量的坐标运算
(1)a=(a1,a2,a3), b=(b1,b2,b3).(2)空间两点间的距离公式
设A(x1,y1,z1),B(x2,y2,z2),
则|AB|=
1.已知空间四边形ABCD中,G为CD的中点,则 +
( + )等于 ( )
A. B.
C. D.
解析: + ( + )= + = .
答案:A
2.下列命题中,不正确的命题个数是 ( )
①空间任意五边形ABCDE,则 =0;
②若a∥b,则a所在直线与b所在直线平行;
③空间任意两非零向量a、b共面;
④空间向量a平行于平面α,则a所在直线平行于平面α.
A.1 B.2
C.3 D.4
.解析:由向量加法知①正确;当a∥b时,a与b所在直线平行或重合,故②是错误的;很明显③是正确的;根据向量与平面平行的定义知,④是错误的.
答案:B
3.已知a=(λ+1,0,2λ),b=(6,2μ-1,2),若a∥b,则λ与μ
的值分别为 ( )
A. B.
C.5,2 D.-5,-2
解析:a∥b?答案:A
4.已知a=(a1,a2,a3),b=(b1,b2,b3),且|a|=5,|b|
=6,a·b=30,则 = .解析:∵|a|=5,|b|=6,∴a·b=|a||b|cos〈a,b〉
=30cos〈a,b〉=30,∴cos〈a,b〉=1,∴a=λb(λ>0),
从而25=36λ2,λ= ,∴ =λ= .
答案:
5.已知空间三点A(1,1,1),B(-1,0,4),C(2,-2,3),则
与 的夹角θ 的大小是 .解析: =(-2,-1,3), =(-1,3,-2),
∴| |= ,| |= , · =-7.
∴cosθ = =- ,∴θ =120°.
答案:120°
用已知向量表示未知向量,一定要结合图形,以图形为指导是解题的关键.
1.把要表示的向量标在封闭图形中,表示为其他向量的和
差的形式,进而寻找这些向量与基向量的关系.
2.用基向量表示一个向量时,如果此向量的起点是从基底
的公共点出发的,一般考虑用加法,否则考虑用减法,
如果此向量与一个易求的向量共线,可用数乘.
专题讲解 如图,在长方体ABCD-
A1B1C1D1中,O为AC的中点.
(1)化简: ;
(2)设E是棱DD1上的点,且
= ,若 =x +y +z ,试求x、y、z的值.
[思路点拨]
[课堂笔记]如图所示,平行六面体ABCD-A1B1C1D1中,E、F分别在B1B和D1D上,且BE= BB1,DF=
DD1.
(1)证明: = + ;
(2)若 =x +y +z ,求x+y+z.
解:(1)证明:1.点共线问题
证明点共线问题可转化为证明向量共线问题,如证明A、
B、C三点共线,即证明 与 共线.
2.点共面问题
点共面问题,可转化为向量共面问题,要证明P、A、B、
C四点共面,只要能证明 =x +y ,或对空间任一点O,有 或
(x+y+z=1)即可,以上结论是判定空间四点共面的一个充要条件,共面向量定理实际上也是三个非零向量所在直线共面的必要条件.
[思路点拨]
四点共面,考虑构造有关向量,然后利用共面向量定理证明. 用向量数量积的定义及性质可解决立体几何中求异面直线所成的角,求两点距离或线段长度以及证明线线垂直,线面垂直等典型问题.
1.求向量m和n所成的角,首先应选择合适的基底,将目标
向量m和n用该组基底表示出来,再求他们的数量积及自
身长度,最后利用公式cos〈m,n〉= .
2.在向量性质中|a|2=a·a提供了向量与实数相互转化的
工具,运用此公式,可使线段长度的计算问题转化成
两个相等向量的数量积的计算问题.
[特别警示] 求向量的数量积关键是求出两个向量的模和夹角.
在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB和CD成60°角(见下图).求B、D间的距离.[思路点拨]
[课堂笔记] ∵∠ACD=90°,∴ =0.
同理 · =0.
∵AB和CD成60°角,∴〈 〉=60°或120°.
=3+2×1×1×cos〈 〉
=
∴| |=2或 ,即B、D间的距离为2或 .
[考题印证]
(2010·珠海模拟)(12分)已知正三棱
柱ABC-A1B1C1,底面边长AB=2,
AB1⊥BC1,点O、O1分别是边AC、
A1C1的中点,建立如图所示的空间
直角坐标系.
(1)求正三棱柱的侧棱长;
(2)若M为BC1的中点,试用基向量 、 、 表示向量
(3)求异面直线AM与BC所成的角.
【解】 (1)设正三棱柱的侧棱长为a,则
A(0,-1,0),B1( ,0,a),B( ,0,0),C1(0,1,a),
∴ =( ,1,a), =(- ,1,a).┄┄┄┄(2分)
∵AB1⊥BC1,∴ ,
∴ =0,即-3+1+a2=0,∴a= .
即正三棱柱侧棱长为 .┄┄┄┄┄┄┄┄┄┄┄(5分)
(3)由条件知,〈 〉=120°,〈 〉=60°,〈 〉=90°.
= (-2×2· +2×2× +0)=0,
∴ ,即异面直线AM与BC所成角为90°.(12分)
1.若空间三点A(1,5,-2),B(2,4,1),C(p,3,q+2)共线,则( )
A.p=3,q=2 B.p=2,q=3
C.p=-3,q=-2 D.p=-2,q=-3
解析: =(1,-1,3), =(p-2,-1,q+1),
由题意知,存在实数λ,使 =λ ,即λ=1,p=3,q=2.
答案:A
2.若向量a=(1,λ,2),b=(2,-1,2),a,b夹角的余弦
值为 ,则λ= ( )
A.-2或 B.-2
C.- D.2或-
解析:a·b=2-λ+4=6-λ,|a|= ,|b|=3,
∴cos〈a,b〉= = ,
∴λ=-2或λ= .
答案:A
3.已知四边形ABCD满足: >0,
>0,则该四边形为 ( )
A.平行四边形 B.梯形
C.平面四边形 D.空间四边形
解析:由题意知,∠B,∠C,∠D,∠A的补角均为锐角,故A、B、C均不正确.
答案:D
4.已知向量a与b的夹角为120°,且|a|=|b|=4,那么
b·(2a+b)的值为 .解析:a·b=|a||b|cos〈a,b〉
=4×4×cos120°=-8,
∴b·(2a+b)=2a·b+b2=2×(-8)+42=0.
答案:0
5.如图,AB=AC=BD=1,AB?平面α,
AC⊥平面α,BD⊥AB,BD与平面α成
30°角,则C、D间的距离为 .
解析:∵AC⊥α,∴AC⊥AB,
∴ =0,
过D作DD′⊥α于点D′,则DD′∥CA,
∴〈 〉=120°,
∴ =- ,又 ,∴ =0,
∴| |2=( )2=1+1+1+2×(- )=2,
∴| |= ,即C、D间的距离为 .
答案:
6.如图所示,在空间四边形OABC中,
OA=8,AB=6,AC=4,BC=5,
∠OAC=45°,∠OAB=60°,求
OA与BC所成角的余弦值.
解:∵
故OA与BC所成角的余弦值为 .
2.空间向量的有关定理
[思考探究]
若a与b确定平面为α,则表示a的有向线段与α的关系是怎样的?
提示:可能与α平行,也可能在α内.3.空间向量的数量积及运算律
4.空间向量的坐标运算
(1)a=(a1,a2,a3), b=(b1,b2,b3).(2)空间两点间的距离公式
设A(x1,y1,z1),B(x2,y2,z2),
则|AB|=
1.已知空间四边形ABCD中,G为CD的中点,则 +
( + )等于 ( )
A. B.
C. D.
解析: + ( + )= + = .
答案:A
2.下列命题中,不正确的命题个数是 ( )
①空间任意五边形ABCDE,则 =0;
②若a∥b,则a所在直线与b所在直线平行;
③空间任意两非零向量a、b共面;
④空间向量a平行于平面α,则a所在直线平行于平面α.
A.1 B.2
C.3 D.4
.解析:由向量加法知①正确;当a∥b时,a与b所在直线平行或重合,故②是错误的;很明显③是正确的;根据向量与平面平行的定义知,④是错误的.
答案:B
3.已知a=(λ+1,0,2λ),b=(6,2μ-1,2),若a∥b,则λ与μ
的值分别为 ( )
A. B.
C.5,2 D.-5,-2
解析:a∥b?答案:A
4.已知a=(a1,a2,a3),b=(b1,b2,b3),且|a|=5,|b|
=6,a·b=30,则 = .解析:∵|a|=5,|b|=6,∴a·b=|a||b|cos〈a,b〉
=30cos〈a,b〉=30,∴cos〈a,b〉=1,∴a=λb(λ>0),
从而25=36λ2,λ= ,∴ =λ= .
答案:
5.已知空间三点A(1,1,1),B(-1,0,4),C(2,-2,3),则
与 的夹角θ 的大小是 .解析: =(-2,-1,3), =(-1,3,-2),
∴| |= ,| |= , · =-7.
∴cosθ = =- ,∴θ =120°.
答案:120°
用已知向量表示未知向量,一定要结合图形,以图形为指导是解题的关键.
1.把要表示的向量标在封闭图形中,表示为其他向量的和
差的形式,进而寻找这些向量与基向量的关系.
2.用基向量表示一个向量时,如果此向量的起点是从基底
的公共点出发的,一般考虑用加法,否则考虑用减法,
如果此向量与一个易求的向量共线,可用数乘.
专题讲解 如图,在长方体ABCD-
A1B1C1D1中,O为AC的中点.
(1)化简: ;
(2)设E是棱DD1上的点,且
= ,若 =x +y +z ,试求x、y、z的值.
[思路点拨]
[课堂笔记]如图所示,平行六面体ABCD-A1B1C1D1中,E、F分别在B1B和D1D上,且BE= BB1,DF=
DD1.
(1)证明: = + ;
(2)若 =x +y +z ,求x+y+z.
解:(1)证明:1.点共线问题
证明点共线问题可转化为证明向量共线问题,如证明A、
B、C三点共线,即证明 与 共线.
2.点共面问题
点共面问题,可转化为向量共面问题,要证明P、A、B、
C四点共面,只要能证明 =x +y ,或对空间任一点O,有 或
(x+y+z=1)即可,以上结论是判定空间四点共面的一个充要条件,共面向量定理实际上也是三个非零向量所在直线共面的必要条件.
[思路点拨]
四点共面,考虑构造有关向量,然后利用共面向量定理证明. 用向量数量积的定义及性质可解决立体几何中求异面直线所成的角,求两点距离或线段长度以及证明线线垂直,线面垂直等典型问题.
1.求向量m和n所成的角,首先应选择合适的基底,将目标
向量m和n用该组基底表示出来,再求他们的数量积及自
身长度,最后利用公式cos〈m,n〉= .
2.在向量性质中|a|2=a·a提供了向量与实数相互转化的
工具,运用此公式,可使线段长度的计算问题转化成
两个相等向量的数量积的计算问题.
[特别警示] 求向量的数量积关键是求出两个向量的模和夹角.
在平行四边形ABCD中,AB=AC=1,∠ACD=90°,将它沿对角线AC折起,使AB和CD成60°角(见下图).求B、D间的距离.[思路点拨]
[课堂笔记] ∵∠ACD=90°,∴ =0.
同理 · =0.
∵AB和CD成60°角,∴〈 〉=60°或120°.
=3+2×1×1×cos〈 〉
=
∴| |=2或 ,即B、D间的距离为2或 .
[考题印证]
(2010·珠海模拟)(12分)已知正三棱
柱ABC-A1B1C1,底面边长AB=2,
AB1⊥BC1,点O、O1分别是边AC、
A1C1的中点,建立如图所示的空间
直角坐标系.
(1)求正三棱柱的侧棱长;
(2)若M为BC1的中点,试用基向量 、 、 表示向量
(3)求异面直线AM与BC所成的角.
【解】 (1)设正三棱柱的侧棱长为a,则
A(0,-1,0),B1( ,0,a),B( ,0,0),C1(0,1,a),
∴ =( ,1,a), =(- ,1,a).┄┄┄┄(2分)
∵AB1⊥BC1,∴ ,
∴ =0,即-3+1+a2=0,∴a= .
即正三棱柱侧棱长为 .┄┄┄┄┄┄┄┄┄┄┄(5分)
(3)由条件知,〈 〉=120°,〈 〉=60°,〈 〉=90°.
= (-2×2· +2×2× +0)=0,
∴ ,即异面直线AM与BC所成角为90°.(12分)
1.若空间三点A(1,5,-2),B(2,4,1),C(p,3,q+2)共线,则( )
A.p=3,q=2 B.p=2,q=3
C.p=-3,q=-2 D.p=-2,q=-3
解析: =(1,-1,3), =(p-2,-1,q+1),
由题意知,存在实数λ,使 =λ ,即λ=1,p=3,q=2.
答案:A
2.若向量a=(1,λ,2),b=(2,-1,2),a,b夹角的余弦
值为 ,则λ= ( )
A.-2或 B.-2
C.- D.2或-
解析:a·b=2-λ+4=6-λ,|a|= ,|b|=3,
∴cos〈a,b〉= = ,
∴λ=-2或λ= .
答案:A
3.已知四边形ABCD满足: >0,
>0,则该四边形为 ( )
A.平行四边形 B.梯形
C.平面四边形 D.空间四边形
解析:由题意知,∠B,∠C,∠D,∠A的补角均为锐角,故A、B、C均不正确.
答案:D
4.已知向量a与b的夹角为120°,且|a|=|b|=4,那么
b·(2a+b)的值为 .解析:a·b=|a||b|cos〈a,b〉
=4×4×cos120°=-8,
∴b·(2a+b)=2a·b+b2=2×(-8)+42=0.
答案:0
5.如图,AB=AC=BD=1,AB?平面α,
AC⊥平面α,BD⊥AB,BD与平面α成
30°角,则C、D间的距离为 .
解析:∵AC⊥α,∴AC⊥AB,
∴ =0,
过D作DD′⊥α于点D′,则DD′∥CA,
∴〈 〉=120°,
∴ =- ,又 ,∴ =0,
∴| |2=( )2=1+1+1+2×(- )=2,
∴| |= ,即C、D间的距离为 .
答案:
6.如图所示,在空间四边形OABC中,
OA=8,AB=6,AC=4,BC=5,
∠OAC=45°,∠OAB=60°,求
OA与BC所成角的余弦值.
解:∵
故OA与BC所成角的余弦值为 .
