华师大版八年级下册19.3 正方形的判定与性质 课件(共19张ppt)
文档属性
| 名称 | 华师大版八年级下册19.3 正方形的判定与性质 课件(共19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 991.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 00:00:00 | ||
图片预览




文档简介
(共19张PPT)
19.3 正方形
华东师大·八年级数学下册
思考:在我们的生活中,除了平行四边形、矩形、菱形外,还有什么特殊的平行四边形呢
正方形
正方形有什么性质?怎样判定一个四边形是正方形?
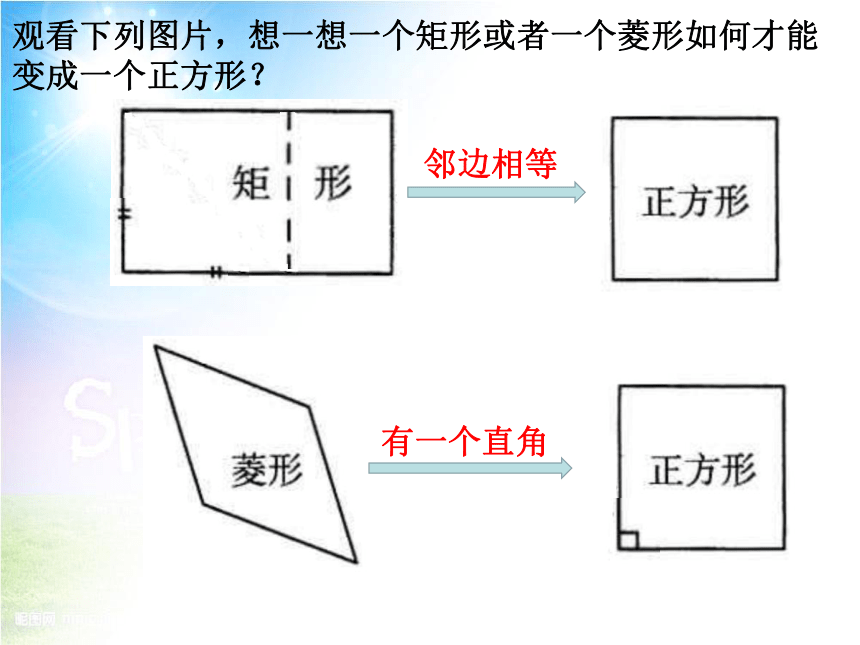
邻边相等
有一个直角
观看下列图片,想一想一个矩形或者一个菱形如何才能变成一个正方形?
正方形的定义:
有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
由定义可知:正方形既是有一组邻边相等的矩形,又是有一个直角的菱形。那它就应该具备菱形和矩形的所有性质。
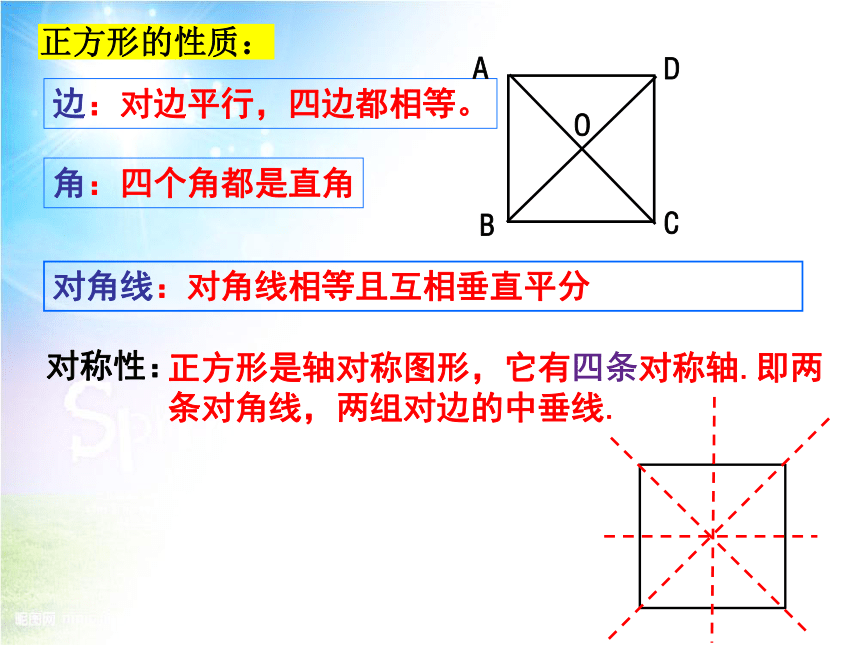
正方形的性质:
边:对边平行,四边都相等。
角:四个角都是直角
对角线:对角线相等且互相垂直平分
A
B
C
D
O
对称性:
正方形是轴对称图形,它有四条对称轴.即两条对角线,两组对边的中垂线.
1. 正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每一条对角线平分一组对角
C
随堂练习
A
B
C
D
O
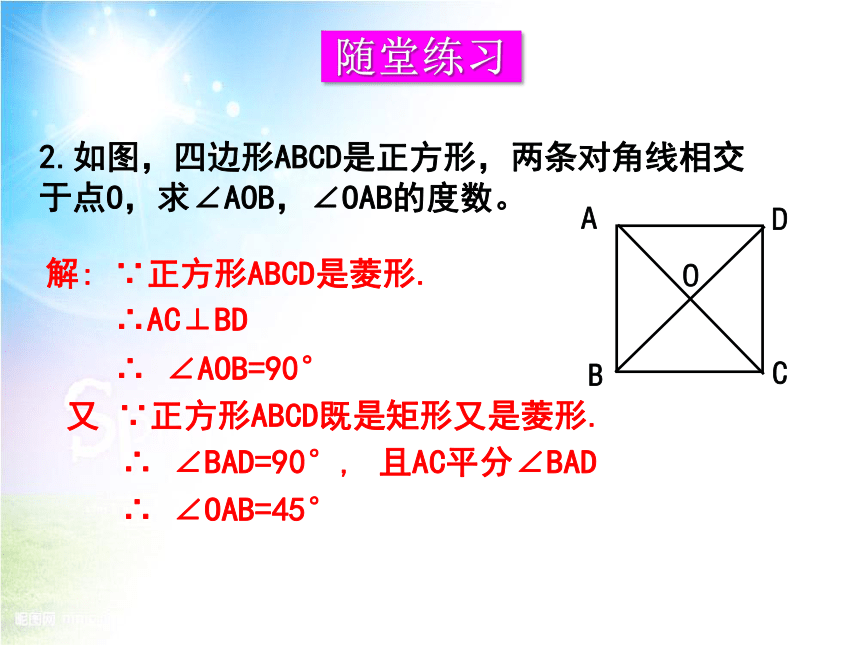
解: ∵正方形ABCD是菱形.
∴AC⊥BD
∴ ∠AOB=90°
又 ∵正方形ABCD既是矩形又是菱形.
∴ ∠BAD=90°, 且AC平分∠BAD
∴ ∠OAB=45°
2.如图,四边形ABCD是正方形,两条对角线相交于点O,求∠AOB,∠OAB的度数。
随堂练习
例1、已知:如图,在正方形ABCD中,点 E在AC上.
求证:BE=DE
证明:∵四边形ABCD 是正方形,
∴AB=AD, ∠BAC=∠DAC.
在△ABC和△ADC中
AB=AD
∠BAC=∠DAC.
AE=AE
∴△ABC≌△ADC (SAS)
∴BE=DE (全等三角形的对应边相等)
A
B
C
D
E
例题讲解
正方形ABCD中,E是BC延长线上一点,且CE=AC, AE交DC于点F,试求∠E, ∠AFC的度数
解:
∵四边形ABCD为正方形,
∵CE=AC
∴∠E=∠CAE
∵∠ACB是⊿ACE的一个外角
∴∠ACB=∠E+∠CAE=2∠E
∵∠AFC是△CEF的一个外角
∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°
∴∠E=22.5°, ∠AFC=112.5°
j
F
E
A
B
D
C
巩固练习
(1)先证它是矩形,再证它有一组邻边相等;
(2)先证它是菱形,再证它有一个角为直角.
思考:那么,如何判定一个四边形是正方形呢?
判定一个四边形为正方形的主要依据是定义,途径有两条:
正方形的判定:
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
思考:那么,如何判定一个四边形是正方形呢?
正方形的判定:
通过以上探索,你觉得什么样的四边形是正方形呢
讨论
1、要使一个菱形成为正方形需要增加的条件是( )。
2、要使一个矩形成为正方形需添加的条件是( )。
3、要使一个平行四边形成为正方形需要增加的条件是:( )。
有一个角是直角
有一组邻边相等
有一组邻边相等且有一个角是直角
思考:正方形、菱形、矩形、平行四边形之间有什么关系?与同学们讨论一下.
平行四边形
菱
形
正方形
平行四边形
矩形
正方形
----下列说法对吗
1.四个角都相等的四边形是正方形.
2.四条边都相等的四边形是正方形.
3.对角线相等的菱形是正方形.
4.对角线垂直的平行四边形是正方形.
5.对角线互相垂直平分且相等的四边形是正方形.
6.四条边相等且有一个角是直角的四边形是正方形.
7.对角线互相垂直的矩形是正方形.
8.对角线垂直且相等的四边形是正方形.
9.四边相等,有一角是直角的四边形是正方形.
╳
√
╳
╳
√
√
√
╳
√
随堂练习
例2、如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.
求证: 四边形CFDE是正方形.
证明 ∵ CD平分∠ACB, DE⊥BC, DF⊥AC,
∴ DE=DF(角平分线上的点到角的两边距离相等).
∵ ∠DEC=∠ECF=∠CFD=90°,
∴ 四边形CFDE是矩形(有三个角是直角的四边形是矩形),
∴ 四边形CFDE是正方形(有一组邻边相等的矩形是正方形).
例题讲解
例3、求证:对角线垂直平分且相等的四边形是正方形。
已知:如图,四边形ABCD中对角线AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。
求证:四边形ABCD是正方形。
证明: ∵AO=CO,BO=DO
∴四边形ABCD是平行四边形又AC=BD
∴平行四边形ABCD是矩形
又∵AC⊥BD
∴平行四边形ABCD是菱形,
即四边形ABCD是正方形
解题小结:正方形即是特殊的矩形,又是特殊的菱形。它没有明确的判定定理,要判定一个四边形是正方形,基本思路就是证明这个四边形既是菱形又是矩形,从而得到这个四边形是正方形。
请大家先根据题意,画出图形然后写出已知、求证.
在选择填空题时可以使用该结论,证明题中也必须证明才可以使用。
边 角 对角线
平行四边形 对边平行且相等 对角相等 对角线互相平分
矩形 对边平行且相等 四个角都是直角 对角线互相平分、相等
菱形 对边平行,四条边相等 对角相等 对角线互相垂直、平分
正方形 对边平行,四条边相等 四个角都是直角 对角线互相垂直、平分且相等
归纳小结
随堂练习
1、在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
C
2、如图,四边形ABCD是正方形,点G是BC上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F,求证:AF-BF=EF.
证明:∵∠BAF+∠DAE=90°,
又∵DE⊥AG,BF∥DE,∴BF⊥AG,∴∠BAF+∠ABF=90°,
∴∠ABF=∠DAE.
又∵AB=DA,∠AFB=∠DEA=90°,
∴△ABF≌△DAE,
∴BF=AE,∴AF-BF=AF-AE=EF.
随堂练习
19.3 正方形
华东师大·八年级数学下册
思考:在我们的生活中,除了平行四边形、矩形、菱形外,还有什么特殊的平行四边形呢
正方形
正方形有什么性质?怎样判定一个四边形是正方形?
邻边相等
有一个直角
观看下列图片,想一想一个矩形或者一个菱形如何才能变成一个正方形?
正方形的定义:
有一组邻边相等且有一个角是直角的平行四边形叫做正方形。
由定义可知:正方形既是有一组邻边相等的矩形,又是有一个直角的菱形。那它就应该具备菱形和矩形的所有性质。
正方形的性质:
边:对边平行,四边都相等。
角:四个角都是直角
对角线:对角线相等且互相垂直平分
A
B
C
D
O
对称性:
正方形是轴对称图形,它有四条对称轴.即两条对角线,两组对边的中垂线.
1. 正方形具有而菱形不一定具有的性质是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.每一条对角线平分一组对角
C
随堂练习
A
B
C
D
O
解: ∵正方形ABCD是菱形.
∴AC⊥BD
∴ ∠AOB=90°
又 ∵正方形ABCD既是矩形又是菱形.
∴ ∠BAD=90°, 且AC平分∠BAD
∴ ∠OAB=45°
2.如图,四边形ABCD是正方形,两条对角线相交于点O,求∠AOB,∠OAB的度数。
随堂练习
例1、已知:如图,在正方形ABCD中,点 E在AC上.
求证:BE=DE
证明:∵四边形ABCD 是正方形,
∴AB=AD, ∠BAC=∠DAC.
在△ABC和△ADC中
AB=AD
∠BAC=∠DAC.
AE=AE
∴△ABC≌△ADC (SAS)
∴BE=DE (全等三角形的对应边相等)
A
B
C
D
E
例题讲解
正方形ABCD中,E是BC延长线上一点,且CE=AC, AE交DC于点F,试求∠E, ∠AFC的度数
解:
∵四边形ABCD为正方形,
∵CE=AC
∴∠E=∠CAE
∵∠ACB是⊿ACE的一个外角
∴∠ACB=∠E+∠CAE=2∠E
∵∠AFC是△CEF的一个外角
∴∠AFC=∠E+∠FCE=22.5°+90°=112.5°
∴∠E=22.5°, ∠AFC=112.5°
j
F
E
A
B
D
C
巩固练习
(1)先证它是矩形,再证它有一组邻边相等;
(2)先证它是菱形,再证它有一个角为直角.
思考:那么,如何判定一个四边形是正方形呢?
判定一个四边形为正方形的主要依据是定义,途径有两条:
正方形的判定:
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
平行四边形
有一个角是直角
有一组邻边相等
思考:那么,如何判定一个四边形是正方形呢?
正方形的判定:
通过以上探索,你觉得什么样的四边形是正方形呢
讨论
1、要使一个菱形成为正方形需要增加的条件是( )。
2、要使一个矩形成为正方形需添加的条件是( )。
3、要使一个平行四边形成为正方形需要增加的条件是:( )。
有一个角是直角
有一组邻边相等
有一组邻边相等且有一个角是直角
思考:正方形、菱形、矩形、平行四边形之间有什么关系?与同学们讨论一下.
平行四边形
菱
形
正方形
平行四边形
矩形
正方形
----下列说法对吗
1.四个角都相等的四边形是正方形.
2.四条边都相等的四边形是正方形.
3.对角线相等的菱形是正方形.
4.对角线垂直的平行四边形是正方形.
5.对角线互相垂直平分且相等的四边形是正方形.
6.四条边相等且有一个角是直角的四边形是正方形.
7.对角线互相垂直的矩形是正方形.
8.对角线垂直且相等的四边形是正方形.
9.四边相等,有一角是直角的四边形是正方形.
╳
√
╳
╳
√
√
√
╳
√
随堂练习
例2、如图,△ABC中,∠ACB=90°,CD平分∠ACB,DE⊥BC, DF⊥AC,垂足分别为E、F.
求证: 四边形CFDE是正方形.
证明 ∵ CD平分∠ACB, DE⊥BC, DF⊥AC,
∴ DE=DF(角平分线上的点到角的两边距离相等).
∵ ∠DEC=∠ECF=∠CFD=90°,
∴ 四边形CFDE是矩形(有三个角是直角的四边形是矩形),
∴ 四边形CFDE是正方形(有一组邻边相等的矩形是正方形).
例题讲解
例3、求证:对角线垂直平分且相等的四边形是正方形。
已知:如图,四边形ABCD中对角线AC、BD相交于点O,且AC=BD,AO=CO, BO=DO,AC⊥BD。
求证:四边形ABCD是正方形。
证明: ∵AO=CO,BO=DO
∴四边形ABCD是平行四边形又AC=BD
∴平行四边形ABCD是矩形
又∵AC⊥BD
∴平行四边形ABCD是菱形,
即四边形ABCD是正方形
解题小结:正方形即是特殊的矩形,又是特殊的菱形。它没有明确的判定定理,要判定一个四边形是正方形,基本思路就是证明这个四边形既是菱形又是矩形,从而得到这个四边形是正方形。
请大家先根据题意,画出图形然后写出已知、求证.
在选择填空题时可以使用该结论,证明题中也必须证明才可以使用。
边 角 对角线
平行四边形 对边平行且相等 对角相等 对角线互相平分
矩形 对边平行且相等 四个角都是直角 对角线互相平分、相等
菱形 对边平行,四条边相等 对角相等 对角线互相垂直、平分
正方形 对边平行,四条边相等 四个角都是直角 对角线互相垂直、平分且相等
归纳小结
随堂练习
1、在四边形ABCD中,O是对角线的交点,能判定这个四边形是正方形的是( )
A.AC=BD,AB∥CD,AB=CD
B.AD∥BC,∠A=∠C
C.AO=BO=CO=DO,AC⊥BD
D.AO=CO,BO=DO,AB=BC
C
2、如图,四边形ABCD是正方形,点G是BC上的任意一点,DE⊥AG于点E,BF∥DE,交AG于点F,求证:AF-BF=EF.
证明:∵∠BAF+∠DAE=90°,
又∵DE⊥AG,BF∥DE,∴BF⊥AG,∴∠BAF+∠ABF=90°,
∴∠ABF=∠DAE.
又∵AB=DA,∠AFB=∠DEA=90°,
∴△ABF≌△DAE,
∴BF=AE,∴AF-BF=AF-AE=EF.
随堂练习
