8.6.3 平面与平面垂直(第1课时)平面与平面垂直的判定 课件(共22张PPT)
文档属性
| 名称 | 8.6.3 平面与平面垂直(第1课时)平面与平面垂直的判定 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 634.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 21:55:27 | ||
图片预览





文档简介
(共22张PPT)
人教2019A版必修 第二册
8.6.3 平面与平面垂直
第1课时 平面与平面垂直的判定
第八章 立体几何初步
1.在立体几何中,“异面直线所成的角”是怎样定义的?
直线a、b是异面直线,经过空间任意一点O,分别引直线a' //a, b'// b,我们把相交直线a' 和 b'所成的锐角 (或直角)叫做异面直线所成的角.
2.在立体几何中,"直线和平面所成的角"是怎样定义的?
平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.
范围:( 0o, 90o ].
范围:[ 0o, 90o ].
复习
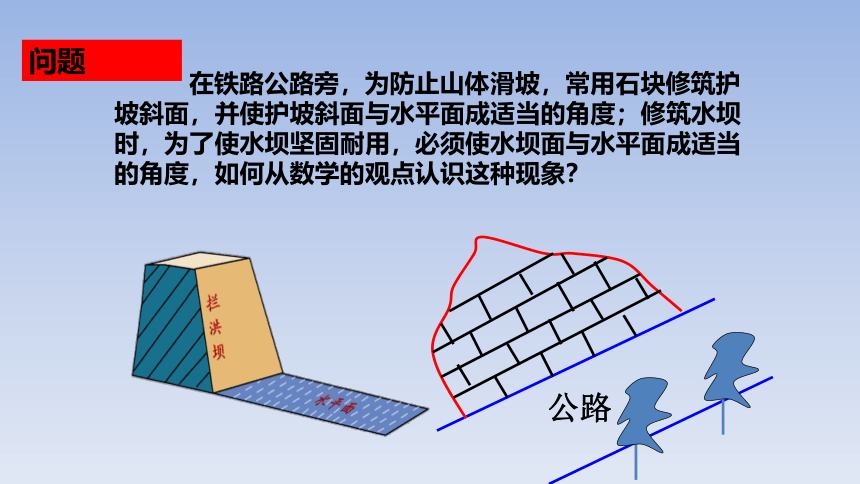
在铁路公路旁,为防止山体滑坡,常用石块修筑护坡斜面,并使护坡斜面与水平面成适当的角度;修筑水坝时,为了使水坝坚固耐用,必须使水坝面与水平面成适当的角度,如何从数学的观点认识这种现象?
公路
问题
(1) 半平面的定义
1.二面角的概念
平面内的一条直线把平面分为两部分,其中的每一部分都叫做半平面.
半平面
半平面
(2) 二面角的定义
从一条直线出发的两个半平面所组成的图形叫做二面角.
这条直线叫做二面角的棱,每个半平面叫做二面角的面.
棱
面
面
①平卧式:
②直立式:
l
l
A
B
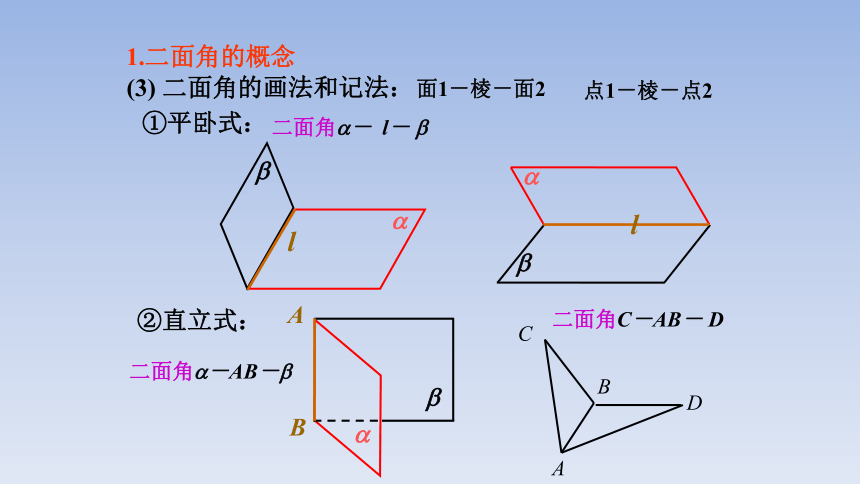
(3) 二面角的画法和记法:
1.二面角的概念
面1-棱-面2
点1-棱-点2
二面角 - l-
二面角 -AB-
二面角C-AB- D
A
B
C
D
思考:我们常说“把门开大些”,是指哪个角开大一些,
你认为应该怎么刻画二面角的大小?
A
O
l
B
二面角的平面角
A'
B'
O'
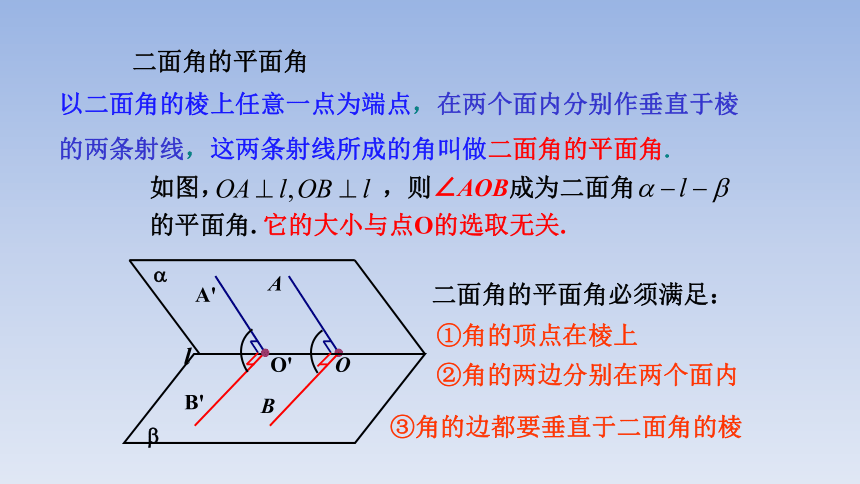
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
如图, ,则∠AOB成为二面角 的平面角. 它的大小与点O的选取无关.
二面角的平面角必须满足:
③角的边都要垂直于二面角的棱
①角的顶点在棱上
②角的两边分别在两个面内
8
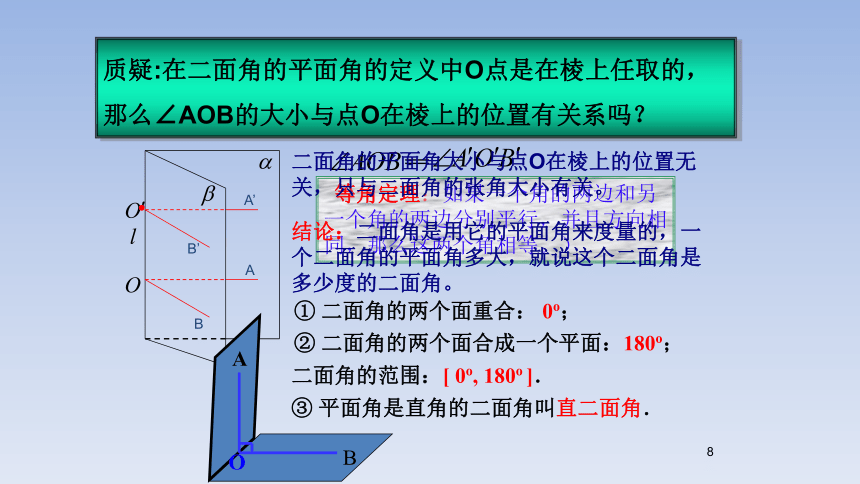
质疑:在二面角的平面角的定义中O点是在棱上任取的,那么∠AOB的大小与点O在棱上的位置有关系吗?
==
等角定理:如果一个角的两边和另
一个角的两边分别平行,并且方向相
同,那么这两个角相等。)
A
B
A’
B’
二面角的平面角大小与点O在棱上的位置无关,只与二面角的张角大小有关。
结论:二面角是用它的平面角来度量的,一个二面角的平面角多大,就说这个二面角是多少度的二面角。
.
二面角的范围:[ 0o, 180o ].
① 二面角的两个面重合: 0o;
② 二面角的两个面合成一个平面:180o;
③ 平面角是直角的二面角叫直二面角.
O
A
B
观察:教室相邻的两个墙面与地面可以构成几个二面角?分别指出构成
这些二面角的面、棱、平面角及其度数。
三个
β
α
α
β
图形表示
平面与平面垂直的定义
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
记作α⊥β
建筑工人砌墙时,如何使所砌的墙和水平面垂直?
应用于生活
铅垂线→直线
墙面→平面
水平面→平面
B
A
C
平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直.
α
β
a
A
简记:线面垂直,则面面垂直
符号:
面面垂直
线面垂直
线线垂直
例1.如图,在正方体 中,求证:平面
证明:
是正方体
又
例2 如图,AB是圆O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点, 求证:平面PAC⊥平面PBC.
AB是圆O直径
PA⊥面ABC
BC 面ABC
BC⊥AC
BC⊥PA
BC⊥面PAC
平面PAC⊥平面PBC
证明:
设已知⊙O平面为α
达标检测
C
D
D
一:平面与平面垂直的判定
小结
二:数学思想:转化思想
面面垂直
线面垂直
线线垂直
1.定义:两个相交平面所成二面角为
直二面角
2.判定定理:在一个平面内找到另
一个平面的垂线
人教2019A版必修 第二册
8.6.3 平面与平面垂直
第1课时 平面与平面垂直的判定
第八章 立体几何初步
1.在立体几何中,“异面直线所成的角”是怎样定义的?
直线a、b是异面直线,经过空间任意一点O,分别引直线a' //a, b'// b,我们把相交直线a' 和 b'所成的锐角 (或直角)叫做异面直线所成的角.
2.在立体几何中,"直线和平面所成的角"是怎样定义的?
平面的一条斜线和它在平面上的射影所成的锐角,叫做这条直线和这个平面所成的角.
范围:( 0o, 90o ].
范围:[ 0o, 90o ].
复习
在铁路公路旁,为防止山体滑坡,常用石块修筑护坡斜面,并使护坡斜面与水平面成适当的角度;修筑水坝时,为了使水坝坚固耐用,必须使水坝面与水平面成适当的角度,如何从数学的观点认识这种现象?
公路
问题
(1) 半平面的定义
1.二面角的概念
平面内的一条直线把平面分为两部分,其中的每一部分都叫做半平面.
半平面
半平面
(2) 二面角的定义
从一条直线出发的两个半平面所组成的图形叫做二面角.
这条直线叫做二面角的棱,每个半平面叫做二面角的面.
棱
面
面
①平卧式:
②直立式:
l
l
A
B
(3) 二面角的画法和记法:
1.二面角的概念
面1-棱-面2
点1-棱-点2
二面角 - l-
二面角 -AB-
二面角C-AB- D
A
B
C
D
思考:我们常说“把门开大些”,是指哪个角开大一些,
你认为应该怎么刻画二面角的大小?
A
O
l
B
二面角的平面角
A'
B'
O'
以二面角的棱上任意一点为端点,在两个面内分别作垂直于棱的两条射线,这两条射线所成的角叫做二面角的平面角.
如图, ,则∠AOB成为二面角 的平面角. 它的大小与点O的选取无关.
二面角的平面角必须满足:
③角的边都要垂直于二面角的棱
①角的顶点在棱上
②角的两边分别在两个面内
8
质疑:在二面角的平面角的定义中O点是在棱上任取的,那么∠AOB的大小与点O在棱上的位置有关系吗?
==
等角定理:如果一个角的两边和另
一个角的两边分别平行,并且方向相
同,那么这两个角相等。)
A
B
A’
B’
二面角的平面角大小与点O在棱上的位置无关,只与二面角的张角大小有关。
结论:二面角是用它的平面角来度量的,一个二面角的平面角多大,就说这个二面角是多少度的二面角。
.
二面角的范围:[ 0o, 180o ].
① 二面角的两个面重合: 0o;
② 二面角的两个面合成一个平面:180o;
③ 平面角是直角的二面角叫直二面角.
O
A
B
观察:教室相邻的两个墙面与地面可以构成几个二面角?分别指出构成
这些二面角的面、棱、平面角及其度数。
三个
β
α
α
β
图形表示
平面与平面垂直的定义
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说这两个平面互相垂直.
记作α⊥β
建筑工人砌墙时,如何使所砌的墙和水平面垂直?
应用于生活
铅垂线→直线
墙面→平面
水平面→平面
B
A
C
平面与平面垂直的判定定理
一个平面过另一个平面的垂线,则这两个平面垂直.
α
β
a
A
简记:线面垂直,则面面垂直
符号:
面面垂直
线面垂直
线线垂直
例1.如图,在正方体 中,求证:平面
证明:
是正方体
又
例2 如图,AB是圆O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点, 求证:平面PAC⊥平面PBC.
AB是圆O直径
PA⊥面ABC
BC 面ABC
BC⊥AC
BC⊥PA
BC⊥面PAC
平面PAC⊥平面PBC
证明:
设已知⊙O平面为α
达标检测
C
D
D
一:平面与平面垂直的判定
小结
二:数学思想:转化思想
面面垂直
线面垂直
线线垂直
1.定义:两个相交平面所成二面角为
直二面角
2.判定定理:在一个平面内找到另
一个平面的垂线
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
