第十章 概率 小结与回顾 课件(共29张PPT)
文档属性
| 名称 | 第十章 概率 小结与回顾 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-14 22:13:12 | ||
图片预览






文档简介
(共29张PPT)
人教2019 A版 必修 第二册
小 结 与 回 顾
第十章 概率
概率是对随机事件发生可能性大小的度量,它已渗透到我们的日常生活中,成为一个常用词汇.
例如,游戏中的随机现象,有抛掷硬币,抛掷骰子,抽取扑克牌,电脑游戏;生活中的随机现象,有彩票,出生月份,摸球抽签儿,上学迟到等;实际应用中的随机现象,有随机抽样,保险问题,投资理财等.
知识梳理
问题导学
1.你能举出一些随机现象的例子吗?你会用什么方法了解这个随机现象的规律?
2.你能举出几个在日常生活中利用概率决策的例子吗?
3.古典概型有哪些特征?
4.由概率的基本性质,你还能推出概率的其他性质吗?
5.如果两个事件A和B独立,那么P(AB)与P(A),P(B)有什么关系?
6.重复试验100次一定比重复试验50次得到的频率更接近概率吗?你有办法了解你得到的频率是否接近概率吗?
7.利用随机模拟得到的计算结果是频率还是概率
(1)概率的研究对象
随机现象
随机试验
有限性
随机性
稳定性
知识回顾
随机事件
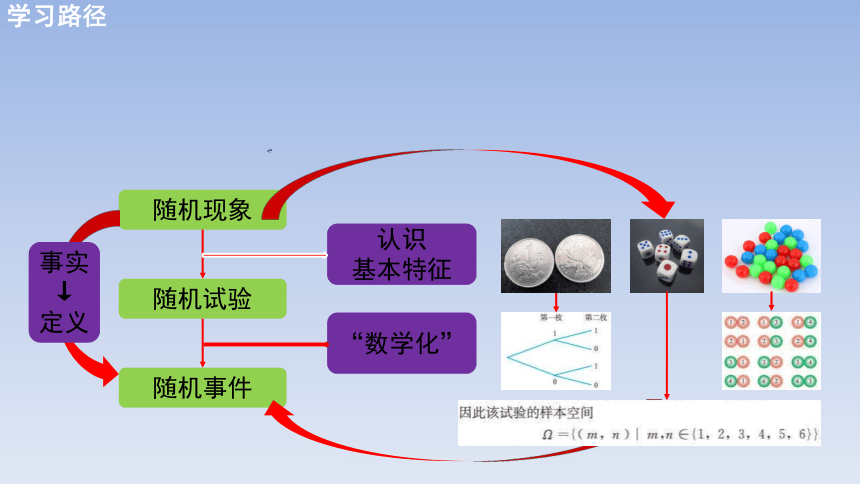
随机现象
随机试验
认识
基本特征
“数学化”
事实
↓
定义
学习路径
例1.在一个盒子中有3个球,蓝球、红球、绿球各1个,从中随
机地取出一个球,观察其颜色后放回,然后再随机取出1个球.请
(1)用适当的符号表示试验的可能结果,写出试验的样本空间;
(2)用集合表示“第一次取出的是红球”的事件;
(3)用集合表示“两次取出的球颜色相同”的事件.
g
r
b
g
b
r
b
g
典例解析
解:(1)用r表示“取出红球”,b表示“取出蓝球”,
g表示“取出绿球”,样本空间Ω={rr,rb,rg,br,bb,bg,gr,gb,gg};
(2)事件“第一次取出的是红球”={rr,rb,rg};
(3)事件“两次取出的球颜色相同”={rr,bb,gg}.
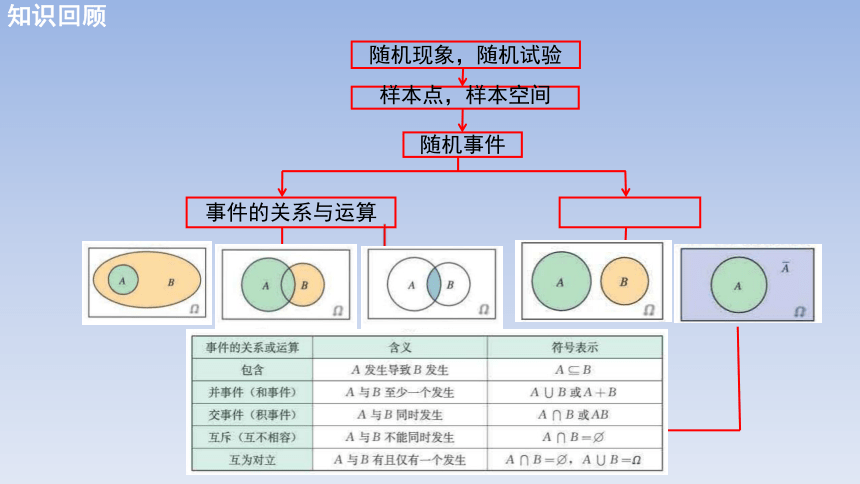
随机现象,随机试验
事件的关系与运算
样本点,样本空间
随机事件
知识回顾
4
典例解析
随机现象,随机试验
事件的关系与运算
事件的概率
样本点,样本空间
随机事件
古典概型
有限性
等可能性
知识回顾
典例解析
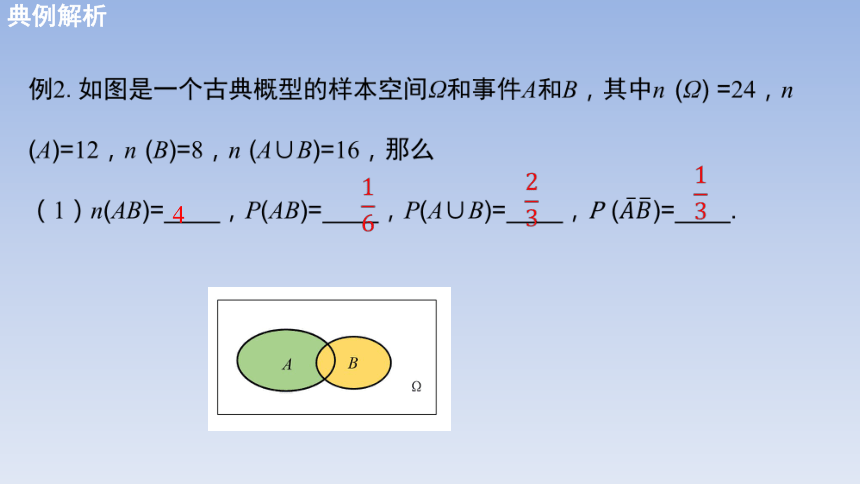
知识回顾
A
B
Ω
典例解析
B
例5.一个袋子中有4个红球,6个绿球,采用不放回方式从中依次随机地取出2个球.
(1)求第二次取到红球的概率;
(2)求两次取到的球颜色相同的概率;
典例解析
随机现象,随机试验
事件的关系与运算
事件的概率
样本点,样本空间
随机事件
事件的独立性
概率的计算
古典概型
概率的基本性质
直观意义
数学本质
知识回顾
4
典例解析
互斥事件一定不独立,独立事件一定不互斥.
7.某同学做立定投篮训练,共做3组,每组投篮次数和命中的次数如下表所示.
第一组 第二组 第三组 合计
投篮次数 100 200 300 600
命中的次数 68 125 176 369
命中的频率 0.68 0.625 0.587 0.615
根据表中的数据信息用频率估计一次投篮命中的概率,那么使误差较小的可能性大的估计值是________.
0.615
频率的稳定性
例7.某同学做立定投篮训练,共做3组,每组投篮次数和命中的次数如下表所示.
典例解析
1.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是___________.
解析
前五场中有一场客场输时,甲队以4∶1获胜的概率是0.63×0.5×0.5×2=0.108;
前五场中有一场主场输时,甲队以4∶1获胜的概率是0.4×0.6×2×0.52×0.6=0.072.
综上所述,甲队以4∶1获胜的概率是0.108+0.072=0.18.
答案 0.18
当堂达标
2. 2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
(1)应从老、中、青员工中分别抽取多少人
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
解析 (1)由已知,老、中、青员工人数之比为6∶9∶10,由于采用分层抽样的方法从中抽取25位员工,因此应从老、中、青员工中分别抽取6人,9人,10人.
(2)①从已知的6人中随机抽取2人的所有可能结果为{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F},共15种.
②由表格知,符合题意的所有可能结果为{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},{C,E},{C,F},{D,F},{E,F},共11种.
所以,事件M发生的概率P(M)= .
3.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
课堂小结
体会数学思想、方法
1.类比的思想
2.函数的思想
3.集合的思想
4.特殊到一般的思想
5.模型化思想
6.化归与转化的思想
7.分类讨论的思想
数学抽象
人教2019 A版 必修 第二册
小 结 与 回 顾
第十章 概率
概率是对随机事件发生可能性大小的度量,它已渗透到我们的日常生活中,成为一个常用词汇.
例如,游戏中的随机现象,有抛掷硬币,抛掷骰子,抽取扑克牌,电脑游戏;生活中的随机现象,有彩票,出生月份,摸球抽签儿,上学迟到等;实际应用中的随机现象,有随机抽样,保险问题,投资理财等.
知识梳理
问题导学
1.你能举出一些随机现象的例子吗?你会用什么方法了解这个随机现象的规律?
2.你能举出几个在日常生活中利用概率决策的例子吗?
3.古典概型有哪些特征?
4.由概率的基本性质,你还能推出概率的其他性质吗?
5.如果两个事件A和B独立,那么P(AB)与P(A),P(B)有什么关系?
6.重复试验100次一定比重复试验50次得到的频率更接近概率吗?你有办法了解你得到的频率是否接近概率吗?
7.利用随机模拟得到的计算结果是频率还是概率
(1)概率的研究对象
随机现象
随机试验
有限性
随机性
稳定性
知识回顾
随机事件
随机现象
随机试验
认识
基本特征
“数学化”
事实
↓
定义
学习路径
例1.在一个盒子中有3个球,蓝球、红球、绿球各1个,从中随
机地取出一个球,观察其颜色后放回,然后再随机取出1个球.请
(1)用适当的符号表示试验的可能结果,写出试验的样本空间;
(2)用集合表示“第一次取出的是红球”的事件;
(3)用集合表示“两次取出的球颜色相同”的事件.
g
r
b
g
b
r
b
g
典例解析
解:(1)用r表示“取出红球”,b表示“取出蓝球”,
g表示“取出绿球”,样本空间Ω={rr,rb,rg,br,bb,bg,gr,gb,gg};
(2)事件“第一次取出的是红球”={rr,rb,rg};
(3)事件“两次取出的球颜色相同”={rr,bb,gg}.
随机现象,随机试验
事件的关系与运算
样本点,样本空间
随机事件
知识回顾
4
典例解析
随机现象,随机试验
事件的关系与运算
事件的概率
样本点,样本空间
随机事件
古典概型
有限性
等可能性
知识回顾
典例解析
知识回顾
A
B
Ω
典例解析
B
例5.一个袋子中有4个红球,6个绿球,采用不放回方式从中依次随机地取出2个球.
(1)求第二次取到红球的概率;
(2)求两次取到的球颜色相同的概率;
典例解析
随机现象,随机试验
事件的关系与运算
事件的概率
样本点,样本空间
随机事件
事件的独立性
概率的计算
古典概型
概率的基本性质
直观意义
数学本质
知识回顾
4
典例解析
互斥事件一定不独立,独立事件一定不互斥.
7.某同学做立定投篮训练,共做3组,每组投篮次数和命中的次数如下表所示.
第一组 第二组 第三组 合计
投篮次数 100 200 300 600
命中的次数 68 125 176 369
命中的频率 0.68 0.625 0.587 0.615
根据表中的数据信息用频率估计一次投篮命中的概率,那么使误差较小的可能性大的估计值是________.
0.615
频率的稳定性
例7.某同学做立定投篮训练,共做3组,每组投篮次数和命中的次数如下表所示.
典例解析
1.甲、乙两队进行篮球决赛,采取七场四胜制(当一队赢得四场胜利时,该队获胜,决赛结束).根据前期比赛成绩,甲队的主客场安排依次为“主主客客主客主”.设甲队主场取胜的概率为0.6,客场取胜的概率为0.5,且各场比赛结果相互独立,则甲队以4∶1获胜的概率是___________.
解析
前五场中有一场客场输时,甲队以4∶1获胜的概率是0.63×0.5×0.5×2=0.108;
前五场中有一场主场输时,甲队以4∶1获胜的概率是0.4×0.6×2×0.52×0.6=0.072.
综上所述,甲队以4∶1获胜的概率是0.108+0.072=0.18.
答案 0.18
当堂达标
2. 2019年,我国施行个人所得税专项附加扣除办法,涉及子女教育、继续教育、大病医疗、住房贷款利息或者住房租金、赡养老人等六项专项附加扣除.某单位老、中、青员工分别有72,108,120人,现采用分层抽样的方法,从该单位上述员工中抽取25人调查专项附加扣除的享受情况.
(1)应从老、中、青员工中分别抽取多少人
(2)抽取的25人中,享受至少两项专项附加扣除的员工有6人,分别记为A,B,C,D,E,F.享受情况如下表,其中“○”表示享受,“×”表示不享受.现从这6人中随机抽取2人接受采访.
①试用所给字母列举出所有可能的抽取结果;
②设M为事件“抽取的2人享受的专项附加扣除至少有一项相同”,求事件M发生的概率.
解析 (1)由已知,老、中、青员工人数之比为6∶9∶10,由于采用分层抽样的方法从中抽取25位员工,因此应从老、中、青员工中分别抽取6人,9人,10人.
(2)①从已知的6人中随机抽取2人的所有可能结果为{A,B},{A,C},{A,D},{A,E},{A,F},{B,C},{B,D},{B,E},{B,F},{C,D},{C,E},{C,F},{D,E},{D,F},{E,F},共15种.
②由表格知,符合题意的所有可能结果为{A,B},{A,D},{A,E},{A,F},{B,D},{B,E},{B,F},{C,E},{C,F},{D,F},{E,F},共11种.
所以,事件M发生的概率P(M)= .
3.某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:[20,30),[30,40),…,[80,90],并整理得到如下频率分布直方图:
(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间[40,50)内的人数;
(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等.试估计总体中男生和女生人数的比例.
课堂小结
体会数学思想、方法
1.类比的思想
2.函数的思想
3.集合的思想
4.特殊到一般的思想
5.模型化思想
6.化归与转化的思想
7.分类讨论的思想
数学抽象
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
