集合的基本运算

课件23张PPT。1.1.3 集合的基本运算第二课时 补集的基本运算提出问题2.对于任意两个集合，是否都可以进行交与并的运算？1.对于集合A，B， 和 的含义如何？ 3.两个集合之间的运算除了“并”与“交”以外，还有其他运算吗？知识探究（一）: 全集思考1:方程 在有理数范围内的
解是什么？在实数范围内的解是什么？思考2:不等式 在实数范围内的解集
是什么？在整数范围内的解集是什么？ 思考3:在不同范围内研究同一个问题，可能有不同的结果.我们通常把研究问题前给定的范围所对应的集合称为全集，如Q，R，Z等.那么全集的含义如何呢？ 提示：如果一个集合含有所研究问题中涉及的所有元素，则称这个集合为全集，通常记作U. 知识探究（二）：补集思考1:在上述各组集合中，集合U，A，B三者之
间有哪些关系？思考2:在上述各组集合中，把集合U看成全集，我们称集合B为集合A相对于全集U的补集.一般地，集合A相对于全集U的补集是由哪些元素组成的？
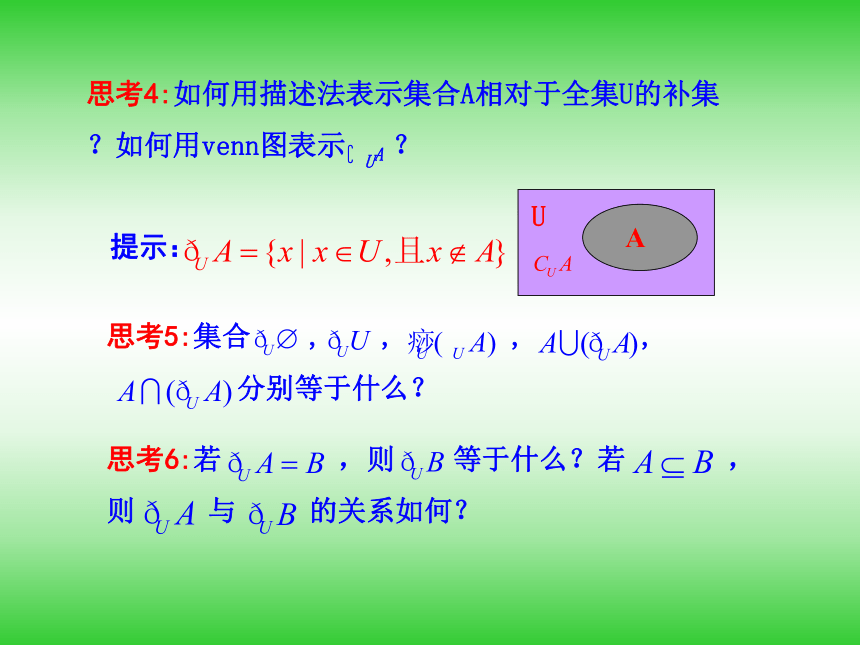
提示：由全集U中不属于集合A的所有元素组成的.思考3:怎样定义“补集”？用什么符号表示集合A相对于全集U的补集？提示：对于一个集合A，由全集U中不属于集合A的所有元素组成的集合，称为集合A相对于全集U的补集.记作?UA . 思考4:如何用描述法表示集合A相对于全集U的补集
？如何用venn图表示?UA ？思考6:若 ，则 等于什么？若 ，
则 与 的关系如何？ 提示： 理论迁移考点一： 补集的简单运算[例1]　设全集U＝{2,3，a2＋2a－3}，A＝{|2a－1|,2}，?U A＝{5}，则a 的值为________．[一点通]　在进行补集的简单运算时，应首先明确全集，而利用A∪（?UA）＝U求全集U是利用定义解题的常规性思维模式，故进行补集运算时，要紧扣补集定义及补集的性质来解题．1．(2011·四川高考)若全集M＝{1,2,3,4,5}，N＝{2,4}，
则?MN＝ 　　(　　)
A．?　　　　　　　 B．{1,3,5}
C．{2,4} D．{1,2,3,4,5}解析：由题意知?MN＝{1,3,5}．
答案：B解析：∵A＝{1，|a－5|,9}，?UA＝{5,7}，
A∪(?UA)＝{1,5,7,9，|a－5|}＝U，∴|a－5|＝3.
解得a－5＝±3，即a＝8或a＝2.
答案：8或23．设全集U＝{1,3,5,7,9}，A＝{1，|a－5|,9)，?UA＝{5,7}，
则a的值为________．2．已知全集U＝{x|x≥－3}，集合A＝{x|－3＜x≤4}，
则?UA＝________.解析：借助数轴得?UA＝{x|x＝－3，或x>4}．
答案：{x|x＝－3，或x>4}考点二： 集合的交、并、补的综合运算[例2]已知全集U＝{x|x≤4}，集合A＝{x|－2＜x＜3}，
B＝{x|－3≤x≤2}，求A∩B，(?UA)∪B，A∩(?U B )，?U(A∪B)．[精解详析]　如图所示.∵A＝{x|－2∴?UA＝{x|x≤－2，或3≤x≤4}，
?UB＝{x|x<－3，或2A∩B＝{x|－2故(?UA)∪B＝{x|x≤2，或3≤x≤4}，
A∩(?UB)＝{x|2?U(A∪B)＝{x|x<－3，或3≤x≤4}．[一点通] 1．如果所给集合是有限集，则先把集合中的元素一一列举出来，然后结合补集的定义来求解．在解答过程中常常借助Venn图来求解，这样处理起来，相对来说比较直观、形象且解答时不易出错．
2．如果所给集合是无限集，则常借助数轴，把已知集合及全集分别表示在数轴上，然后进行交、并、补集的运算.解答过程中要注意边界问题．4．设U＝R，A＝{x|x>0}，B＝{x|x>1}，则A∩(?UB)＝(　　)
A．{x|0≤x<1} B．{x|0C．{x|x<0} D．{x|x>1}解析：?UB＝{x|x≤1}，
∴A∩(?UB)＝{x|0答案：B解析：由M∩(?UN)＝{2,4}，可得集合N中不含元素2,4，集合M中含有元素2,4，故N＝{1,3,5}．
答案：B5．(2011·湖南高考)设全集U＝M∪N＝{1,2,3,4,5}，
M∩(?UN)＝{2,4}，则N＝ (　　)
A．{1,2,3} B．{1,3,5}
C．{1,4,5} D．{2,3,4}考点三： 补集的综合应用[例3]　(12分)已知全集U＝R，集合A＝{x|x<－1}，B＝{x|2a2．不等式中的等号在补集中能否取到，要引起重视，还要注意补集是全集的子集．6．已知集合A＝{x|x＝R，则实数a的取值范围是________．解析：?RB＝{x|x≤1，或x≥2}，A＝{x|x0}，若
A∩(?RB)＝?，求实数a的取值范围．解：∵B＝{x|x<－1，或x>0}，
∴?RB＝{x|－1≤x≤0}，
因而要使A∩(?RB)＝?，结合数轴分析(如图)，
可得a≤－1.方法规律小结1．求集合A的补集的前提是A是全集U的子集，所选全集不同，得到的补集也是不同的．
2．?UA的数学意义包括四个方面：
①A?U；
②?UA的每一个元素都属于U，即?UA?U；
③?UA的每一个元素都不属于A，即(?UA)∩A＝?；
④?UA含有U中所有不属于A的元素，即?U(?UA)＝A.3．补集的性质
(1)?UU＝?，?U?＝U；
(2)A∪(?UA)＝U，A∩(?UA)＝?；
(3)?U(?UA)＝A.同学们 再见！