北师大版七年级数学下册 5.3.1 等腰三角形 课件 (共23张PPT)
文档属性
| 名称 | 北师大版七年级数学下册 5.3.1 等腰三角形 课件 (共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1023.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 10:41:27 | ||
图片预览





文档简介
(共23张PPT)
第5章 生活中的轴对称
5.3.1 等腰三角形
北师大版
观察下面的金字塔和人字梁屋架的图片,这些物体的外观结构形式是我们见过的哪一种图形?
等腰三角形
情境导入
什么样的三角形是等腰三角形呢?
底角
底角
顶角
底边
腰
腰
有两个角相等的三角形是等腰三角形.
有两条边相等的三角形是等腰三角形.
复习巩固
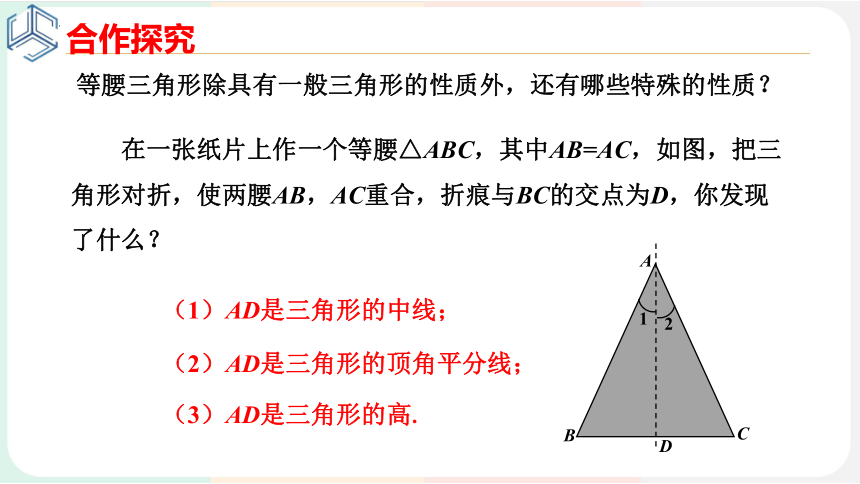
等腰三角形除具有一般三角形的性质外,还有哪些特殊的性质?
在一张纸片上作一个等腰△ABC,其中AB=AC,如图,把三角形对折,使两腰AB,AC重合,折痕与BC的交点为D,你发现了什么?
A
C
B
D
1
2
(1)AD是三角形的中线;
(2)AD是三角形的顶角平分线;
(3)AD是三角形的高.
合作探究
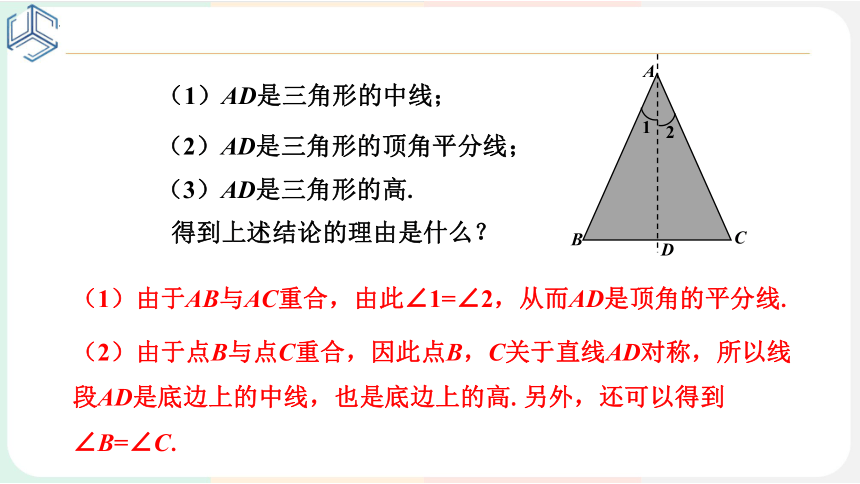
得到上述结论的理由是什么?
A
C
B
D
1
2
(1)由于AB与AC重合,由此∠1=∠2,从而AD是顶角的平分线.
(2)由于点B与点C重合,因此点B,C关于直线AD对称,所以线段AD是底边上的中线,也是底边上的高.另外,还可以得到∠B=∠C.
(1)AD是三角形的中线;
(2)AD是三角形的顶角平分线;
(3)AD是三角形的高.
这样我们可以得到以下结论:
等腰三角形是轴对称图形.
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”).它们所在的直线都是等腰三角形的对称轴.
等腰三角形的两个底角相等.
1.若等腰三角形的一个内角为 40°,则它的另 外两个内角为__________________
2. 若等腰三角形的一个内角为120°,则它的另外两个内角为____
3.一等腰三角形的两边长为2和4,则该等腰三角形的周长为______
4.一等腰三角形的两边长为3和4,则该等腰三角形的周长为______
5.已知等腰三角形的腰长比底边长多2cm,并且它的周长为16cm,求这个等腰三角形的各边长。
70°,70°或40°,100°
30°,30°
10
10或11
等腰三角形三边长为4cm,6cm,6cm。
巩固练习
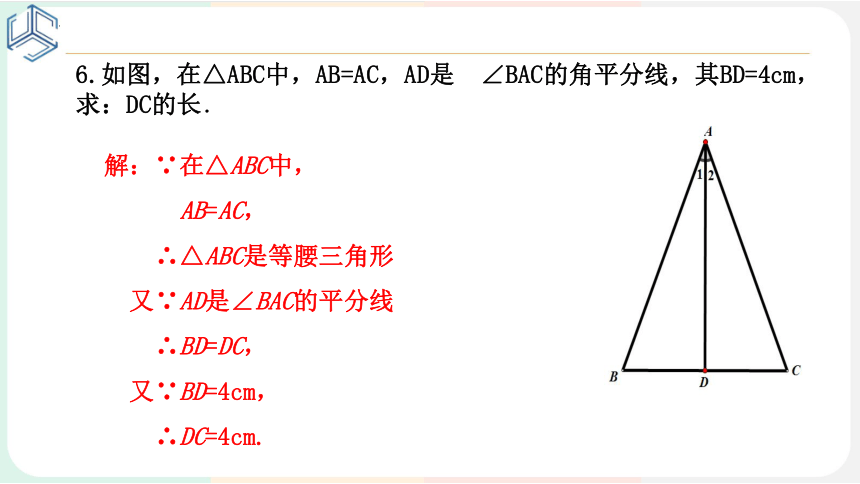
6.如图,在△ABC中,AB=AC,AD是 ∠BAC的角平分线,其BD=4cm,
求:DC的长.
解:∵在△ABC中,
AB=AC,
∴△ABC是等腰三角形
又∵AD是∠BAC的平分线
∴BD=DC,
又∵BD=4cm,
∴DC=4cm.
观察下列图片,寻找共同特点:
通过以上图片,你发现了什么?
从以上图片中抽象出来的图形就是等边三角形.
探究等边三角形的特征
有两边相等的三角形是等腰三角形.
有三边相等的三角形是等边三角形,也称为正三角形.
我们已经知道等腰三角形具有如下特征:
(1)等腰三角形的两个底角相等.
(2)等腰三角形顶角的平分线、底边上的中线和底边上的高重合,简称为“三线合一”.
(3)等腰三角形是轴对称图形.
那么等边三角形是否也具有以上特征呢?为什么?
等边三角形也具有以上特征.因为等边三角形是特殊的等腰三角形.
等边三角形既然是特殊的等腰三角形,那么等边三角形是否还有不同于等腰三角形的特征呢?下面我们一起来探究.
【归纳探究】
每人在本子上画出一个等边三角
形.△ABC是一个特殊的等腰三角形,即等边三角形,根据等腰三角形的两
个底角相等,可以发现∠A=∠B=∠C;因为∠A+∠B+∠C=180°,由此我们
可以得出: ∠A=∠B=∠C=60°.
A
C
B
下面我们写出完整的推理过程:
A
C
B
∵AB=AC,
∴∠B=∠C,
同理∠A=∠B.
∴∠A=∠B=∠C.
又∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
由此你能否总结出等边三角形的特征?
A
C
B
(1)三边之间:
AB_____AC_____BC;
(2)三角之间:
∠A_____∠B_____∠C.
=
=
=
=
由以上探索和观察我们可以得到等边三角形的有关特征:
(1)等边三角形的三边都相等;
(2)等边三角形的三个内角都相等,每一个内角都是60°.
1.如果ΔABC是轴对称图形,则它的对称轴一定是( )
A. 某一条边上的高。
B. 某一条边上的中线。
C. 平分一角和这个角的对边的直线。
D. 某一个角的平分线。
C
巩固练习
2. 在△ABC中,AB=AC,∠B=72°,那么∠A=______
36°
4.如图,在△ABC中,AB=AC时,
(1)因为AD⊥BC
所以∠ ____= ∠_____;____=____
(2) 因为AD是中线
所以____⊥____; ∠_____=∠_____
(3) 因为 AD是角平分线
所以____ ⊥____;____ =____
B
C
A
3.如图,在等腰ΔABC中,AB=AC顶角∠A=100°那么底角∠B=_______∠C =_______ .
40°
40°
BAD
CAD
CD
BD
AD
BC
BAD
CAD
AD
BC
BD
CD
A
B
C
D
5.已知等腰三角形的腰长比底边长多2cm,并且它的周长为16cm,求这个等腰三角形的各边长。
解:设三角形的底边长为xcm,则其腰长为 (x+2)cm,根据题意得:
2(x+2)+x=16
解得 x=4
∴等腰三角形三边长为4cm,6cm,6cm。
解:作AF⊥BC,垂足为F,则AF是
等腰△ABC,△ADE的底边上的高,
也是底边上的中线.
所以BF=CF,DF=EF.
从而BF-DF=CF-EF,
即BD=CE.
6.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,BD与CE相等吗?为什么?
A
C
B
D
E
F
7.如图,在△ACB中,AB=AC,点D在AC上,且BD=BC=AD,∠BDC=∠A+∠ABD,求△ABC各角的度数.
A
C
B
D
解:∵BD=AD,
∴∠A=∠ABD.
∵BD=BC,
∴∠C=∠BDC.
又∵∠BDC=∠A+∠ABD,
∴∠BDC=2∠A.
又∵AB=AC,
∴∠C=∠ABC=∠BDC.
根据三角形内角和∠A+∠C+∠ABC=180°,
即∠A+2∠A+2∠A=180°, ∴∠A=36°∠C=∠ABC=2×36°=72°.
1.等腰三角形是有两边相等的三角形,其中相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
2.等腰三角形是轴对称图形;等腰三角形“三线合一”;等腰三角形的两底角相等.
3.等边三角形的三边都相等;等边三角形的三个内角都相等,每一个内角都是60°.
课堂小结
1.下面是由大小不同的等边三角形组成的图案,请找出它的对称轴.
同步作业
2.墙上钉了一根木条,小明想检验这根木条是否水平.他拿来一个如图所示的测平仪.在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤.小明将BC边与木条重合,观察此时重锤是否通过A点.如果重锤过A点,那么这个木条就是水平的.你能说明其中的道理吗?
A
C
B
D
3.如图,在下面的等腰三角形中,∠A是顶角,分别求出它们的底角的度数.
A
C
B
60°
(1)
A
C
B
(2)
120°
A
C
B
(3)
第5章 生活中的轴对称
5.3.1 等腰三角形
北师大版
观察下面的金字塔和人字梁屋架的图片,这些物体的外观结构形式是我们见过的哪一种图形?
等腰三角形
情境导入
什么样的三角形是等腰三角形呢?
底角
底角
顶角
底边
腰
腰
有两个角相等的三角形是等腰三角形.
有两条边相等的三角形是等腰三角形.
复习巩固
等腰三角形除具有一般三角形的性质外,还有哪些特殊的性质?
在一张纸片上作一个等腰△ABC,其中AB=AC,如图,把三角形对折,使两腰AB,AC重合,折痕与BC的交点为D,你发现了什么?
A
C
B
D
1
2
(1)AD是三角形的中线;
(2)AD是三角形的顶角平分线;
(3)AD是三角形的高.
合作探究
得到上述结论的理由是什么?
A
C
B
D
1
2
(1)由于AB与AC重合,由此∠1=∠2,从而AD是顶角的平分线.
(2)由于点B与点C重合,因此点B,C关于直线AD对称,所以线段AD是底边上的中线,也是底边上的高.另外,还可以得到∠B=∠C.
(1)AD是三角形的中线;
(2)AD是三角形的顶角平分线;
(3)AD是三角形的高.
这样我们可以得到以下结论:
等腰三角形是轴对称图形.
等腰三角形顶角的平分线、底边上的中线、底边上的高重合(也称“三线合一”).它们所在的直线都是等腰三角形的对称轴.
等腰三角形的两个底角相等.
1.若等腰三角形的一个内角为 40°,则它的另 外两个内角为__________________
2. 若等腰三角形的一个内角为120°,则它的另外两个内角为____
3.一等腰三角形的两边长为2和4,则该等腰三角形的周长为______
4.一等腰三角形的两边长为3和4,则该等腰三角形的周长为______
5.已知等腰三角形的腰长比底边长多2cm,并且它的周长为16cm,求这个等腰三角形的各边长。
70°,70°或40°,100°
30°,30°
10
10或11
等腰三角形三边长为4cm,6cm,6cm。
巩固练习
6.如图,在△ABC中,AB=AC,AD是 ∠BAC的角平分线,其BD=4cm,
求:DC的长.
解:∵在△ABC中,
AB=AC,
∴△ABC是等腰三角形
又∵AD是∠BAC的平分线
∴BD=DC,
又∵BD=4cm,
∴DC=4cm.
观察下列图片,寻找共同特点:
通过以上图片,你发现了什么?
从以上图片中抽象出来的图形就是等边三角形.
探究等边三角形的特征
有两边相等的三角形是等腰三角形.
有三边相等的三角形是等边三角形,也称为正三角形.
我们已经知道等腰三角形具有如下特征:
(1)等腰三角形的两个底角相等.
(2)等腰三角形顶角的平分线、底边上的中线和底边上的高重合,简称为“三线合一”.
(3)等腰三角形是轴对称图形.
那么等边三角形是否也具有以上特征呢?为什么?
等边三角形也具有以上特征.因为等边三角形是特殊的等腰三角形.
等边三角形既然是特殊的等腰三角形,那么等边三角形是否还有不同于等腰三角形的特征呢?下面我们一起来探究.
【归纳探究】
每人在本子上画出一个等边三角
形.△ABC是一个特殊的等腰三角形,即等边三角形,根据等腰三角形的两
个底角相等,可以发现∠A=∠B=∠C;因为∠A+∠B+∠C=180°,由此我们
可以得出: ∠A=∠B=∠C=60°.
A
C
B
下面我们写出完整的推理过程:
A
C
B
∵AB=AC,
∴∠B=∠C,
同理∠A=∠B.
∴∠A=∠B=∠C.
又∵∠A+∠B+∠C=180°,
∴∠A=∠B=∠C=60°.
由此你能否总结出等边三角形的特征?
A
C
B
(1)三边之间:
AB_____AC_____BC;
(2)三角之间:
∠A_____∠B_____∠C.
=
=
=
=
由以上探索和观察我们可以得到等边三角形的有关特征:
(1)等边三角形的三边都相等;
(2)等边三角形的三个内角都相等,每一个内角都是60°.
1.如果ΔABC是轴对称图形,则它的对称轴一定是( )
A. 某一条边上的高。
B. 某一条边上的中线。
C. 平分一角和这个角的对边的直线。
D. 某一个角的平分线。
C
巩固练习
2. 在△ABC中,AB=AC,∠B=72°,那么∠A=______
36°
4.如图,在△ABC中,AB=AC时,
(1)因为AD⊥BC
所以∠ ____= ∠_____;____=____
(2) 因为AD是中线
所以____⊥____; ∠_____=∠_____
(3) 因为 AD是角平分线
所以____ ⊥____;____ =____
B
C
A
3.如图,在等腰ΔABC中,AB=AC顶角∠A=100°那么底角∠B=_______∠C =_______ .
40°
40°
BAD
CAD
CD
BD
AD
BC
BAD
CAD
AD
BC
BD
CD
A
B
C
D
5.已知等腰三角形的腰长比底边长多2cm,并且它的周长为16cm,求这个等腰三角形的各边长。
解:设三角形的底边长为xcm,则其腰长为 (x+2)cm,根据题意得:
2(x+2)+x=16
解得 x=4
∴等腰三角形三边长为4cm,6cm,6cm。
解:作AF⊥BC,垂足为F,则AF是
等腰△ABC,△ADE的底边上的高,
也是底边上的中线.
所以BF=CF,DF=EF.
从而BF-DF=CF-EF,
即BD=CE.
6.如图,点D,E在△ABC的边BC上,AB=AC,AD=AE,BD与CE相等吗?为什么?
A
C
B
D
E
F
7.如图,在△ACB中,AB=AC,点D在AC上,且BD=BC=AD,∠BDC=∠A+∠ABD,求△ABC各角的度数.
A
C
B
D
解:∵BD=AD,
∴∠A=∠ABD.
∵BD=BC,
∴∠C=∠BDC.
又∵∠BDC=∠A+∠ABD,
∴∠BDC=2∠A.
又∵AB=AC,
∴∠C=∠ABC=∠BDC.
根据三角形内角和∠A+∠C+∠ABC=180°,
即∠A+2∠A+2∠A=180°, ∴∠A=36°∠C=∠ABC=2×36°=72°.
1.等腰三角形是有两边相等的三角形,其中相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
2.等腰三角形是轴对称图形;等腰三角形“三线合一”;等腰三角形的两底角相等.
3.等边三角形的三边都相等;等边三角形的三个内角都相等,每一个内角都是60°.
课堂小结
1.下面是由大小不同的等边三角形组成的图案,请找出它的对称轴.
同步作业
2.墙上钉了一根木条,小明想检验这根木条是否水平.他拿来一个如图所示的测平仪.在这个测平仪中,AB=AC,BC边的中点D处挂了一个重锤.小明将BC边与木条重合,观察此时重锤是否通过A点.如果重锤过A点,那么这个木条就是水平的.你能说明其中的道理吗?
A
C
B
D
3.如图,在下面的等腰三角形中,∠A是顶角,分别求出它们的底角的度数.
A
C
B
60°
(1)
A
C
B
(2)
120°
A
C
B
(3)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
