北师大版数学七年级下册 第四章 三角形单元 复习课件(共43张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 第四章 三角形单元 复习课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 300.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 11:17:41 | ||
图片预览


文档简介
(共43张PPT)
全等三角形复习
A
B
C
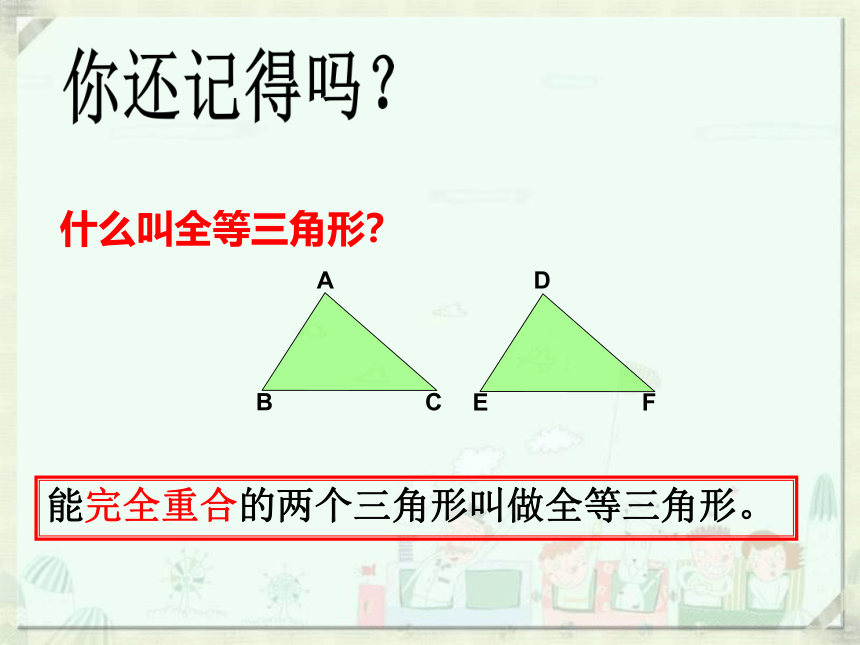
什么叫全等三角形?
能完全重合的两个三角形叫做全等三角形。
你还记得吗?
D
E
F
A
B
C
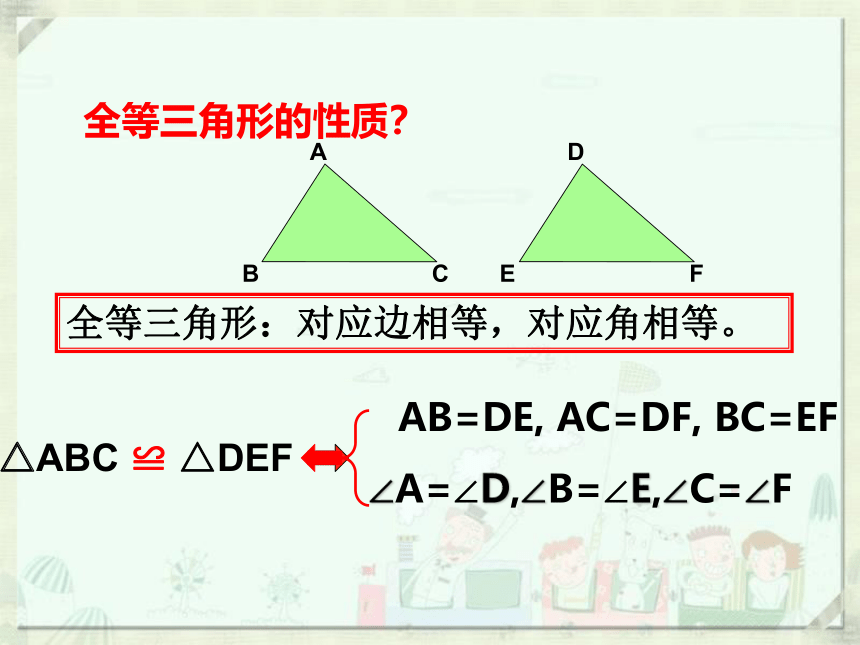
全等三角形的性质?
全等三角形:对应边相等,对应角相等。
△ABC ≌ △DEF
D
E
F
AB=DE, AC=DF, BC=EF
∠A=∠D,∠B=∠E,∠C=∠F
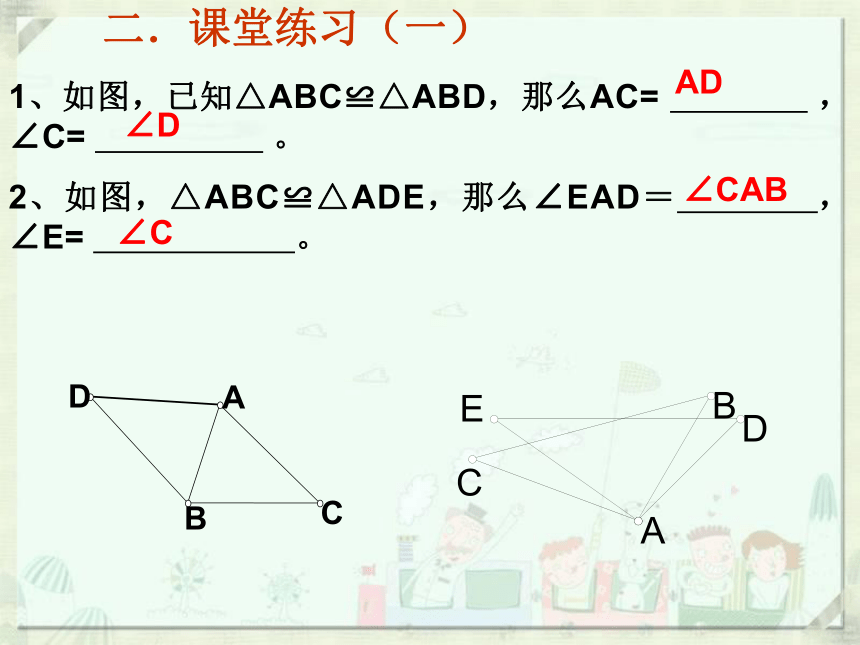
1、如图,已知△ABC≌△ABD,那么AC= ,∠C= 。
2、如图,△ABC≌△ADE,那么∠EAD= ,∠E= 。
D
A
B
C
二.课堂练习(一)
AD
∠D
∠CAB
∠C
5
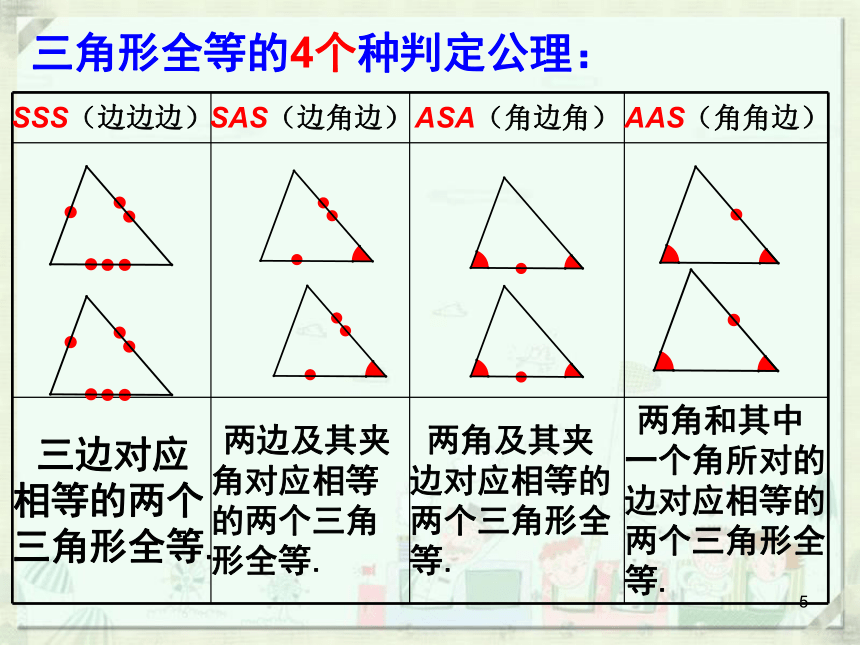
三角形全等的4个种判定公理:
SSS(边边边) SAS(边角边) ASA(角边角) AAS(角角边)
三边对应相等的两个三角形全等. 两边及其夹角对应相等的两个三角形全等. 两角及其夹边对应相等的两个三角形全等. 两角和其中一个角所对的边对应相等的两个三角形全等.
全等判定的格式
在△ABC和△DEF中, ......要判定的三角形
AB=DE(已知)
AC=DF(已知) ......判定条件和理由
BC=EF(已知)
∴△ABC≌△DEF(SSS)......结论及理由
全部需要按对应关系书写,一般先标图进行分析
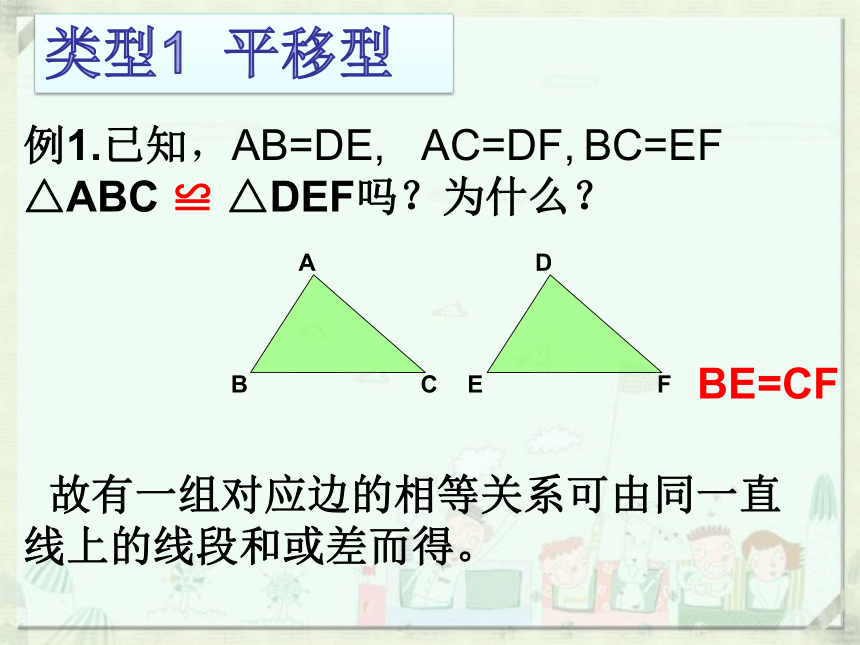
类型1 平移型
A
B
C
例1.已知,AB=DE, AC=DF,
△ABC ≌ △DEF吗?为什么?
BE=CF
D
E
F
BC=EF
故有一组对应边的相等关系可由同一直线上的线段和或差而得。
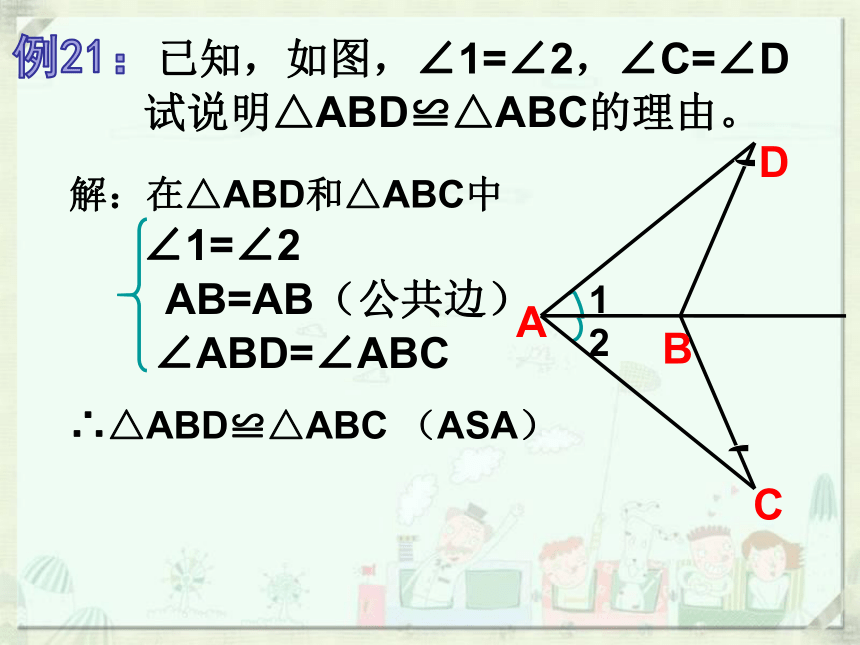
例21:已知,如图,∠1=∠2,∠C=∠D
试说明△ABD≌△ABC的理由。
1
2
C
A
D
B
解:在△ABD和△ABC中
∠1=∠2
AB=AB(公共边)
∠ABD=∠ABC
∴△ABD≌△ABC (ASA)
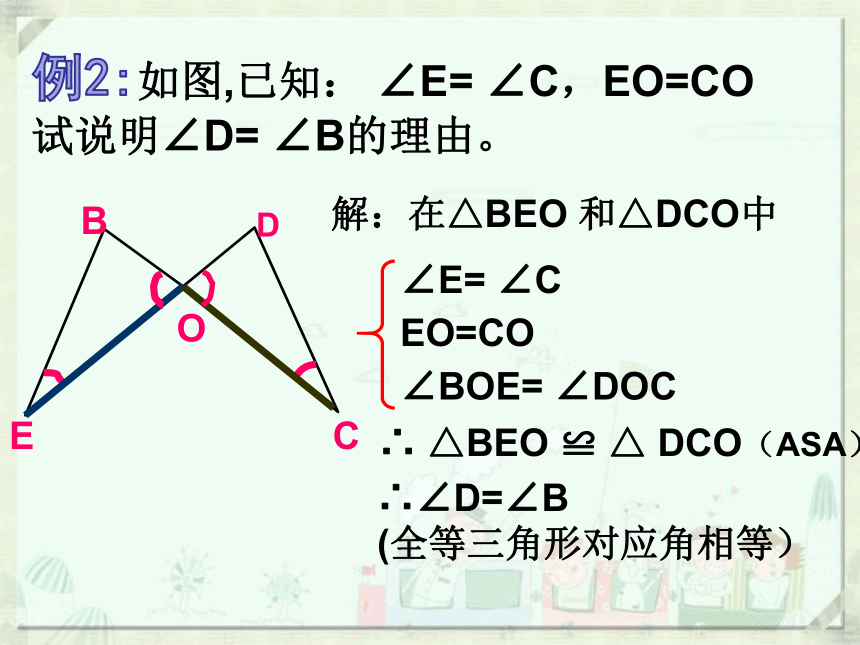
例2:如图,已知: ∠E= ∠C,EO=CO
试说明∠D= ∠B的理由。
B
E
D
C
O
∠E= ∠C
EO=CO
∠BOE= ∠DOC
解:在△BEO 和△DCO中
∴ △BEO ≌ △ DCO(ASA)
∴∠D=∠B
(全等三角形对应角相等)
1
2
C
A
D
B
B
E
D
C
O
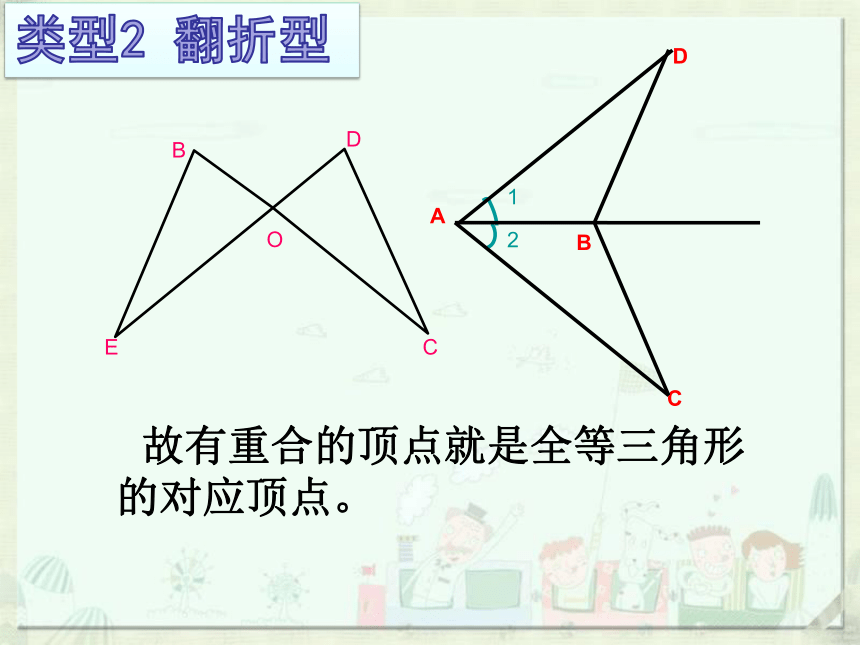
类型2 翻折型
故有重合的顶点就是全等三角形的对应顶点。
B
E
D
C
B
E
D
C
A
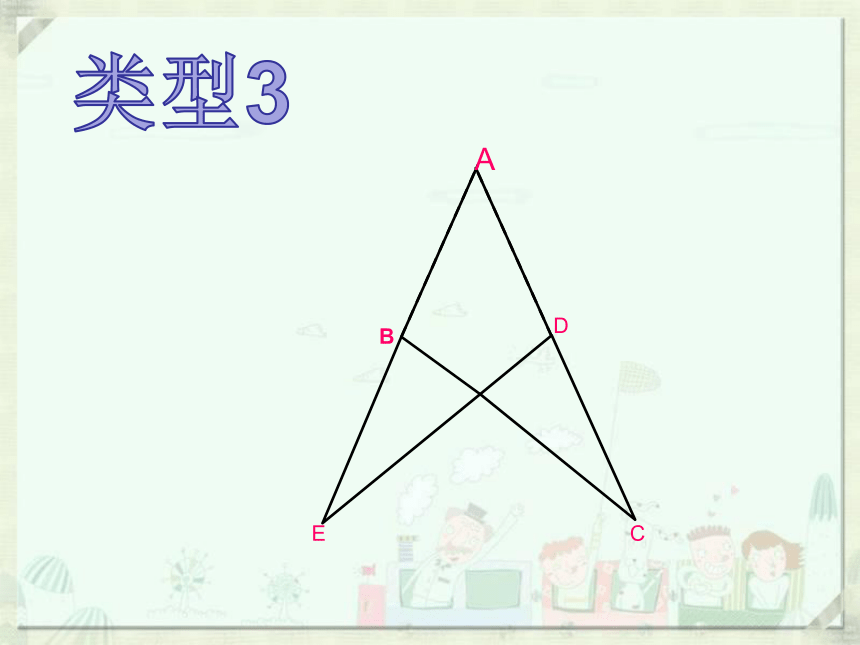
类型3
已知:点D在AC上,点B在AE上,BC和DE相交于点O,AE=AC,∠E=∠C
例3.
B
E
D
C
A
O
(1) △ABC≌△ADE吗?为什么?
(2)BE与DC相等吗?请说明理由.
解 :(1)在△ABC和△ADE中
∵ ∠A=∠A(公共角)
AC=AE(已知)
∠C=∠E(已知)
∴△ABC≌△ADE(ASA)
(2) ∵ △ABC≌△ADE(已证)
∴AB=AD
(全等三角形的对应边相等)
又 ∵AE=AC(已知)
∴ AE-AB=AC-AD
∴BE=DC(等式性质)
A
B
C
D
E
类型4
例4 已知: ∠1= ∠2, ∠E= ∠C,AC=AE
试说明AB=AD ,∠B= ∠D的理由。
A
B
C
D
E
1
2
解: ∵ ∠1= ∠2
∴ ∠1+ ∠EAC= ∠2+ ∠EAC
∴ ∠BAC= ∠DAE
在△BAC和 △DAE中
∵ ∠BAC= ∠DAE
AC=AE(已知)
∠C= ∠E(已知)
∴△ BAC ≌△ DAE (ASA)
∴AB=AD(全等三角形的对应边相等)
∠B=∠D (全等三角形的对应角相等)
A
B
C
D
E
B
A
C
D
E
做一做:
已知: ∠1= ∠2,∠E= ∠C, AC=AE,
D、A、B在一条直线上;试说明点A的位置.
B
A
D
C
E
1
2
3
解:∵ ∠1= ∠2
∴ ∠1+ ∠3= ∠2+ ∠3
∴ ∠ DAE = ∠ BAC
在△DAE和△BAC中
∠ DAE = ∠ BAC
AE=AC
∠E= ∠C
∴ △DAE≌△BAC(ASA)
∴AD=AB
∴点A为线段DB中点
A
B
C
D
E
1
2
B
A
D
C
E
1
2
3
旋转型
故一般有一对相等的角隐含在某些角的和或差中。
全等条件探索
题目往往隐藏个别不需说明的条件,或者给出个别不能直接使用的条件,需要我们自己找出,或者转化为等边或等角使用
全等的判定(公共边)
A
C
B
D
A
C
B
D
全等的判定(部分公共)
A
C
B
D
F
E
全等的判定(公共角)
B
C
A
E
D
O
E
B
A
D
A
C
全等的判定(部分公共)
B
E
A
D
C
B
E
A
A
D
C
全等的判定(互余)
C
B
E
A
D
全等的判定(平行)
A
C
B
D
全等的判定(三线)
B
E
A
D
C
练习 已知AB=AC,BE=CE,
求证:AD⊥BC
D
E
C
A
课堂小结
证明两个三角形全等的基本思路:
找第三边
(SSS)
找夹角
(1):已知两边----
(SAS)
(3):已知一边一角
已知一边和它的邻角
已知一边和它的对角
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找一角(AAS)
(2): 已知两角---
找两角的夹边(ASA)
找夹边外的任意边(AAS)
全等三角形复习
A
B
C
什么叫全等三角形?
能完全重合的两个三角形叫做全等三角形。
你还记得吗?
D
E
F
A
B
C
全等三角形的性质?
全等三角形:对应边相等,对应角相等。
△ABC ≌ △DEF
D
E
F
AB=DE, AC=DF, BC=EF
∠A=∠D,∠B=∠E,∠C=∠F
1、如图,已知△ABC≌△ABD,那么AC= ,∠C= 。
2、如图,△ABC≌△ADE,那么∠EAD= ,∠E= 。
D
A
B
C
二.课堂练习(一)
AD
∠D
∠CAB
∠C
5
三角形全等的4个种判定公理:
SSS(边边边) SAS(边角边) ASA(角边角) AAS(角角边)
三边对应相等的两个三角形全等. 两边及其夹角对应相等的两个三角形全等. 两角及其夹边对应相等的两个三角形全等. 两角和其中一个角所对的边对应相等的两个三角形全等.
全等判定的格式
在△ABC和△DEF中, ......要判定的三角形
AB=DE(已知)
AC=DF(已知) ......判定条件和理由
BC=EF(已知)
∴△ABC≌△DEF(SSS)......结论及理由
全部需要按对应关系书写,一般先标图进行分析
类型1 平移型
A
B
C
例1.已知,AB=DE, AC=DF,
△ABC ≌ △DEF吗?为什么?
BE=CF
D
E
F
BC=EF
故有一组对应边的相等关系可由同一直线上的线段和或差而得。
例21:已知,如图,∠1=∠2,∠C=∠D
试说明△ABD≌△ABC的理由。
1
2
C
A
D
B
解:在△ABD和△ABC中
∠1=∠2
AB=AB(公共边)
∠ABD=∠ABC
∴△ABD≌△ABC (ASA)
例2:如图,已知: ∠E= ∠C,EO=CO
试说明∠D= ∠B的理由。
B
E
D
C
O
∠E= ∠C
EO=CO
∠BOE= ∠DOC
解:在△BEO 和△DCO中
∴ △BEO ≌ △ DCO(ASA)
∴∠D=∠B
(全等三角形对应角相等)
1
2
C
A
D
B
B
E
D
C
O
类型2 翻折型
故有重合的顶点就是全等三角形的对应顶点。
B
E
D
C
B
E
D
C
A
类型3
已知:点D在AC上,点B在AE上,BC和DE相交于点O,AE=AC,∠E=∠C
例3.
B
E
D
C
A
O
(1) △ABC≌△ADE吗?为什么?
(2)BE与DC相等吗?请说明理由.
解 :(1)在△ABC和△ADE中
∵ ∠A=∠A(公共角)
AC=AE(已知)
∠C=∠E(已知)
∴△ABC≌△ADE(ASA)
(2) ∵ △ABC≌△ADE(已证)
∴AB=AD
(全等三角形的对应边相等)
又 ∵AE=AC(已知)
∴ AE-AB=AC-AD
∴BE=DC(等式性质)
A
B
C
D
E
类型4
例4 已知: ∠1= ∠2, ∠E= ∠C,AC=AE
试说明AB=AD ,∠B= ∠D的理由。
A
B
C
D
E
1
2
解: ∵ ∠1= ∠2
∴ ∠1+ ∠EAC= ∠2+ ∠EAC
∴ ∠BAC= ∠DAE
在△BAC和 △DAE中
∵ ∠BAC= ∠DAE
AC=AE(已知)
∠C= ∠E(已知)
∴△ BAC ≌△ DAE (ASA)
∴AB=AD(全等三角形的对应边相等)
∠B=∠D (全等三角形的对应角相等)
A
B
C
D
E
B
A
C
D
E
做一做:
已知: ∠1= ∠2,∠E= ∠C, AC=AE,
D、A、B在一条直线上;试说明点A的位置.
B
A
D
C
E
1
2
3
解:∵ ∠1= ∠2
∴ ∠1+ ∠3= ∠2+ ∠3
∴ ∠ DAE = ∠ BAC
在△DAE和△BAC中
∠ DAE = ∠ BAC
AE=AC
∠E= ∠C
∴ △DAE≌△BAC(ASA)
∴AD=AB
∴点A为线段DB中点
A
B
C
D
E
1
2
B
A
D
C
E
1
2
3
旋转型
故一般有一对相等的角隐含在某些角的和或差中。
全等条件探索
题目往往隐藏个别不需说明的条件,或者给出个别不能直接使用的条件,需要我们自己找出,或者转化为等边或等角使用
全等的判定(公共边)
A
C
B
D
A
C
B
D
全等的判定(部分公共)
A
C
B
D
F
E
全等的判定(公共角)
B
C
A
E
D
O
E
B
A
D
A
C
全等的判定(部分公共)
B
E
A
D
C
B
E
A
A
D
C
全等的判定(互余)
C
B
E
A
D
全等的判定(平行)
A
C
B
D
全等的判定(三线)
B
E
A
D
C
练习 已知AB=AC,BE=CE,
求证:AD⊥BC
D
E
C
A
课堂小结
证明两个三角形全等的基本思路:
找第三边
(SSS)
找夹角
(1):已知两边----
(SAS)
(3):已知一边一角
已知一边和它的邻角
已知一边和它的对角
找这边的另一个邻角(ASA)
找这个角的另一个边(SAS)
找一角(AAS)
(2): 已知两角---
找两角的夹边(ASA)
找夹边外的任意边(AAS)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
