北师大版数学七年级下册 4.3 探索三角形全等的条件( 第1课时)课件 (共17张PPT)
文档属性
| 名称 | 北师大版数学七年级下册 4.3 探索三角形全等的条件( 第1课时)课件 (共17张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 493.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
3 探索三角形全等的条件
第1课时 边边边
北师大版 七年级下册
情境导入
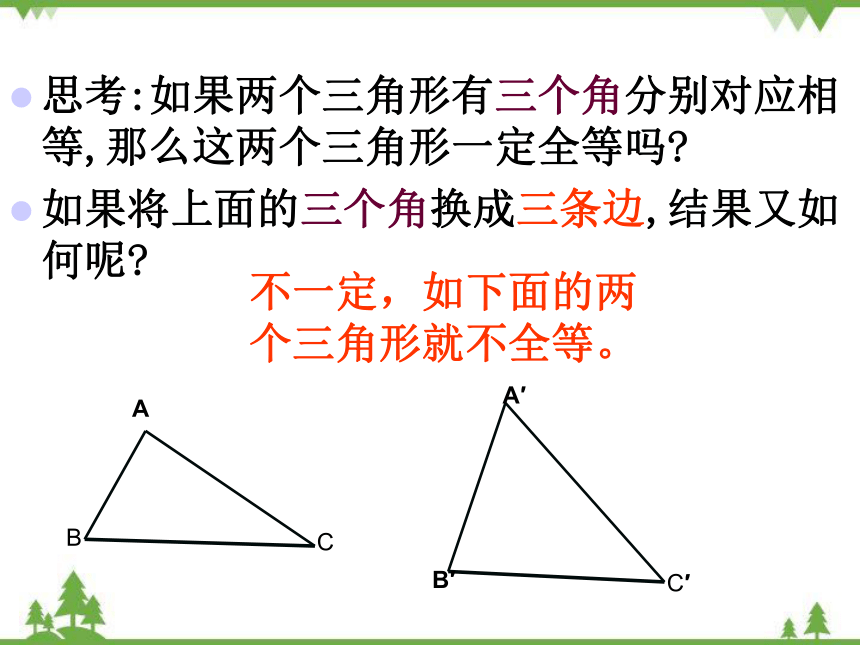
思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗
如果将上面的三个角换成三条边,结果又如何呢
A
B
C
A′
B′
C′
不一定,如下面的两个三角形就不全等。
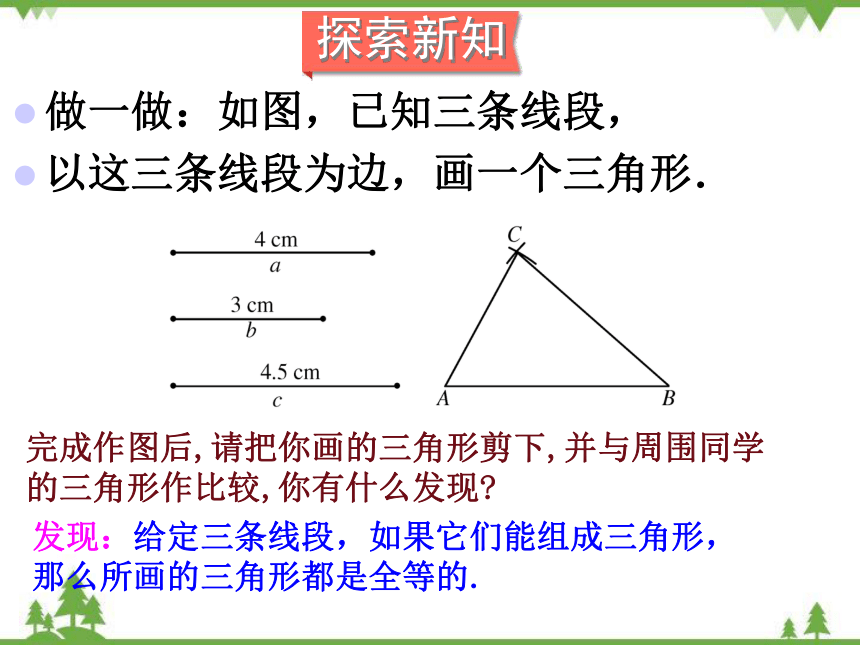
做一做:如图,已知三条线段,
以这三条线段为边,画一个三角形.
完成作图后,请把你画的三角形剪下,并与周围同学的三角形作比较,你有什么发现
发现:给定三条线段,如果它们能组成三角形,那么所画的三角形都是全等的.
探索新知
全等三角形的判定(sss)
边边边公理: 三边 对应 相等的两个三角形全等.
(S.S.S.)
应用表达式:(如图)
A
B
C
D
E
F
在△ABC与△DEF中
∴ △ABC≌△DEF (S.S.S.)
例:如图,在四边形ABCD中,AD=BC, AB=CD.
求证:△ABC≌△CDA.
学以致用
证明:在△ABC和△CDA中,
CB=AD (已知)
AB=CD (已知)
AC=CA (公共边)
∴ △ABC≌△CDA(S.S.S.).
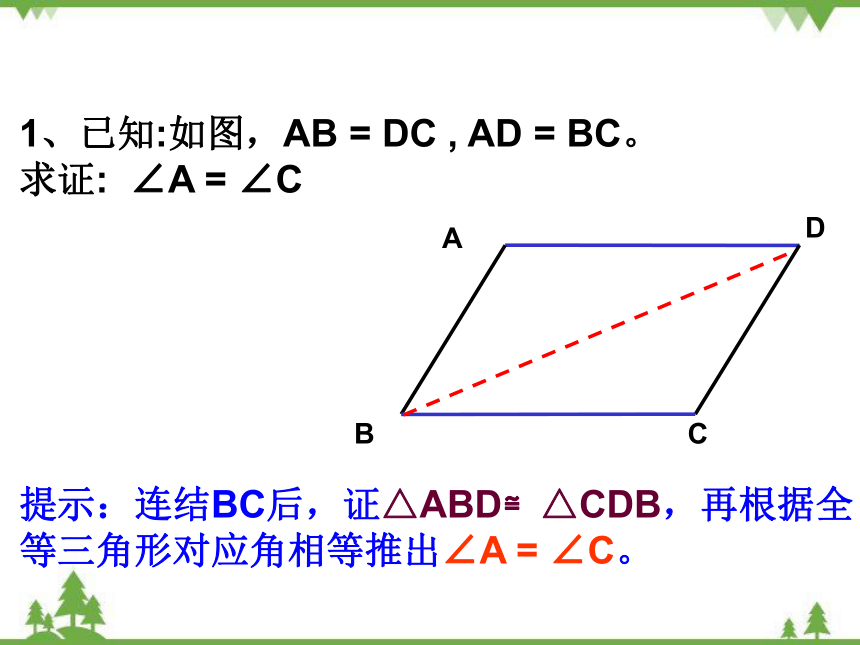
1、已知:如图,AB = DC , AD = BC。
求证: ∠A = ∠C
A
B
D
C
提示:连结BC后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。
对应相等的元素 两边一角 两角一边
三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(S.A.S)
不一定
一定
(A.S.A)
一定
(A.A.S)
不一定
一定
(S.S.S)
判定三角形全等至少有一组边
1. 如图,四边形ABCD是平行四边形,△ABC和△CDA是否全等?若四边形是菱形、矩形、梯形,是否还有相同的结论?
解:①全等(用S.S.S.或S.A.S.或A.S.A.或A.A.S.都能证得)
②因为菱形和矩形都是平行四边形,所以有相同的结论;而梯形不是平行四边形,所以没有相同的结论。
随堂演练
2、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D
A
B
D
C
巩固提高练习
提示:BC为公共边,由S.S.S.可得两三角形全等,全等三角形对应角相等。
2、已知:如图.AB = AD ,BC = DC
求证:∠B= ∠D
A
B
C
D
证明:连结AC
在△ABC与△ADC中
∴ △ABC≌△ADC (S.S.S.)
∴∠B=∠D(全等三角形对应角相等)
(公共边)
3、已知:如图.点B、 E、 C、 F在同一条直
线上, AB = DE , AC = DF,BE = CF
求证: ∠A = ∠D
A
B
D
E
C
F
提示:因为BE+CE=CF+CE,即BC=EF,所以由S.S.S.得⊿ABC≌⊿DEF,所以∠A = ∠D(全等三角形对应角相等)
4、已知:如图.AB = DC , AC = DB,
OA = OD
求证:∠A = ∠D
A
B
D
C
o
证明:∵AC=BD,OA=OD,
∴BD-OD=AC-OA,即
OB=OC.
∵AB=DC,OA=OD,
∴⊿OAB≌⊿ODC(S.S.S.)
∴ ∠A = ∠D(全等三角形对应角相等)
5、已知:如图,△ABC是一个钢架,AB=AC,
AD是连结A与BC中点D的支架.
求证:AD⊥BC
证明:在△ABD与△ACD中
∴ △ABD≌ △ACD (S.S.S.)
∴AD⊥BC (垂直定义)
∴∠1 = ∠BDC=900 (平角定义)
(公共边)
∴∠1 = ∠2 (全等三角形的对应角相等)
A
B
C
D
1
2
想一想
证明两直线垂直或一个角是直角,可转化为证该角和它的邻补角相等
通过这节课的学习活动,你有什么收获?
课堂小结
请说出目前判定三角形全等的4种方法:
S.A.S. A.S.A. A.A.S. S.S.S.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
不要靠馈赠来获得一个朋友。你须贡献你挚情的爱,学习怎样用正当的方法来赢得一个人的心。
—— 苏格拉底
3 探索三角形全等的条件
第1课时 边边边
北师大版 七年级下册
情境导入
思考:如果两个三角形有三个角分别对应相等,那么这两个三角形一定全等吗
如果将上面的三个角换成三条边,结果又如何呢
A
B
C
A′
B′
C′
不一定,如下面的两个三角形就不全等。
做一做:如图,已知三条线段,
以这三条线段为边,画一个三角形.
完成作图后,请把你画的三角形剪下,并与周围同学的三角形作比较,你有什么发现
发现:给定三条线段,如果它们能组成三角形,那么所画的三角形都是全等的.
探索新知
全等三角形的判定(sss)
边边边公理: 三边 对应 相等的两个三角形全等.
(S.S.S.)
应用表达式:(如图)
A
B
C
D
E
F
在△ABC与△DEF中
∴ △ABC≌△DEF (S.S.S.)
例:如图,在四边形ABCD中,AD=BC, AB=CD.
求证:△ABC≌△CDA.
学以致用
证明:在△ABC和△CDA中,
CB=AD (已知)
AB=CD (已知)
AC=CA (公共边)
∴ △ABC≌△CDA(S.S.S.).
1、已知:如图,AB = DC , AD = BC。
求证: ∠A = ∠C
A
B
D
C
提示:连结BC后,证△ABD≌△CDB,再根据全等三角形对应角相等推出∠A = ∠C。
对应相等的元素 两边一角 两角一边
三角
三边
两边及其夹角 两边及其中一边的对角 两角及其夹边 两角及其中一角的对边
三角形是否全等
一定
(S.A.S)
不一定
一定
(A.S.A)
一定
(A.A.S)
不一定
一定
(S.S.S)
判定三角形全等至少有一组边
1. 如图,四边形ABCD是平行四边形,△ABC和△CDA是否全等?若四边形是菱形、矩形、梯形,是否还有相同的结论?
解:①全等(用S.S.S.或S.A.S.或A.S.A.或A.A.S.都能证得)
②因为菱形和矩形都是平行四边形,所以有相同的结论;而梯形不是平行四边形,所以没有相同的结论。
随堂演练
2、已知:如图.AB = DC , AC = DB
求证: ∠A = ∠D
A
B
D
C
巩固提高练习
提示:BC为公共边,由S.S.S.可得两三角形全等,全等三角形对应角相等。
2、已知:如图.AB = AD ,BC = DC
求证:∠B= ∠D
A
B
C
D
证明:连结AC
在△ABC与△ADC中
∴ △ABC≌△ADC (S.S.S.)
∴∠B=∠D(全等三角形对应角相等)
(公共边)
3、已知:如图.点B、 E、 C、 F在同一条直
线上, AB = DE , AC = DF,BE = CF
求证: ∠A = ∠D
A
B
D
E
C
F
提示:因为BE+CE=CF+CE,即BC=EF,所以由S.S.S.得⊿ABC≌⊿DEF,所以∠A = ∠D(全等三角形对应角相等)
4、已知:如图.AB = DC , AC = DB,
OA = OD
求证:∠A = ∠D
A
B
D
C
o
证明:∵AC=BD,OA=OD,
∴BD-OD=AC-OA,即
OB=OC.
∵AB=DC,OA=OD,
∴⊿OAB≌⊿ODC(S.S.S.)
∴ ∠A = ∠D(全等三角形对应角相等)
5、已知:如图,△ABC是一个钢架,AB=AC,
AD是连结A与BC中点D的支架.
求证:AD⊥BC
证明:在△ABD与△ACD中
∴ △ABD≌ △ACD (S.S.S.)
∴AD⊥BC (垂直定义)
∴∠1 = ∠BDC=900 (平角定义)
(公共边)
∴∠1 = ∠2 (全等三角形的对应角相等)
A
B
C
D
1
2
想一想
证明两直线垂直或一个角是直角,可转化为证该角和它的邻补角相等
通过这节课的学习活动,你有什么收获?
课堂小结
请说出目前判定三角形全等的4种方法:
S.A.S. A.S.A. A.A.S. S.S.S.
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
不要靠馈赠来获得一个朋友。你须贡献你挚情的爱,学习怎样用正当的方法来赢得一个人的心。
—— 苏格拉底
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
