沪科版七年级下册 8.3 完全平方公式与平方差公式课件(共15张PPT)
文档属性
| 名称 | 沪科版七年级下册 8.3 完全平方公式与平方差公式课件(共15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 414.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-16 11:57:11 | ||
图片预览



文档简介
(共16张PPT)
完全平方公式与平方差公式(1、2)
教学目标:
1、经历探索平方差公式与完全平方公式的发展过程,发展学生观察、交流、归纳、猜测、验证等能力。
2、会推导乘法公式:
,了解公式的几何背景,会用公式计算。
3、进一步体会数形结合的数学思想和方法。
教材分析:
由多项式的乘法到乘法公式是一般到特殊的认识过程,对它的学习丰富了教学内容,开阔了学生的视野,所以乘法公式的应用是本节内容的重点。难点是公式的结构特征及公式中字母所表示的广泛含义的理解和正确运用。
(a±b) 2 =
a2±2ab+b2
(a+b)(a-b) =
a 2- b2
2、你记得多项式乘法法则吗?
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
(a+b)(a-b) =
(a+b) 2 =
(a-b) 2 =
a2+2ab+b2
a 2- b2
a2-2ab+b2
1、你能写出a与b的平方和和a与b和的平方分别是什么吗?
一、复习导入
a 2+b2
(a+b)2
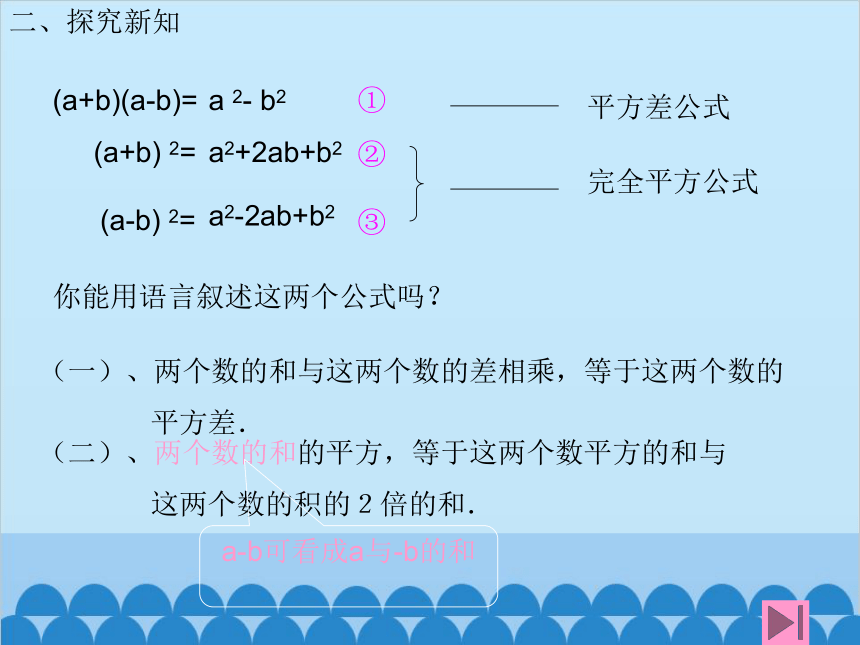
平方差公式
(a+b)(a-b)=
a 2- b2
①
(a+b) 2=
(a-b) 2=
a2+2ab+b2
a2-2ab+b2
②
③
完全平方公式
你能用语言叙述这两个公式吗?
(二)、两个数的和的平方,等于这两个数平方的和与
这两个数的积的2倍的和.
(一)、两个数的和与这两个数的差相乘,等于这两个数的
平方差.
a-b可看成a与-b的和
二、探究新知
三、交流
a
b
a
b
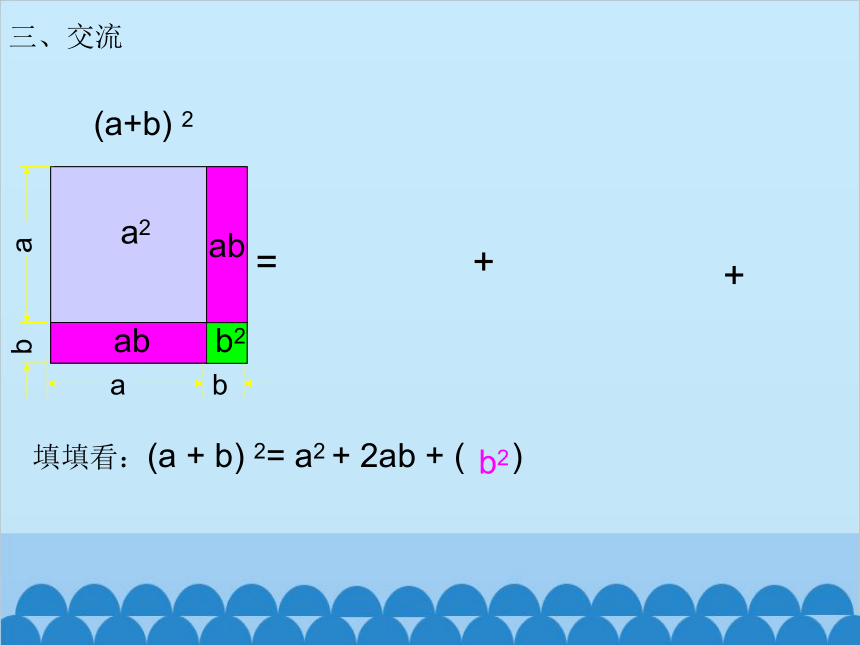
(a+b) 2
a2
b2
+
+
=
填填看:(a + b) 2= a2 + 2ab + ( )
b2
ab
ab
ab
a
a2
b2
+
-
=
b
a
b
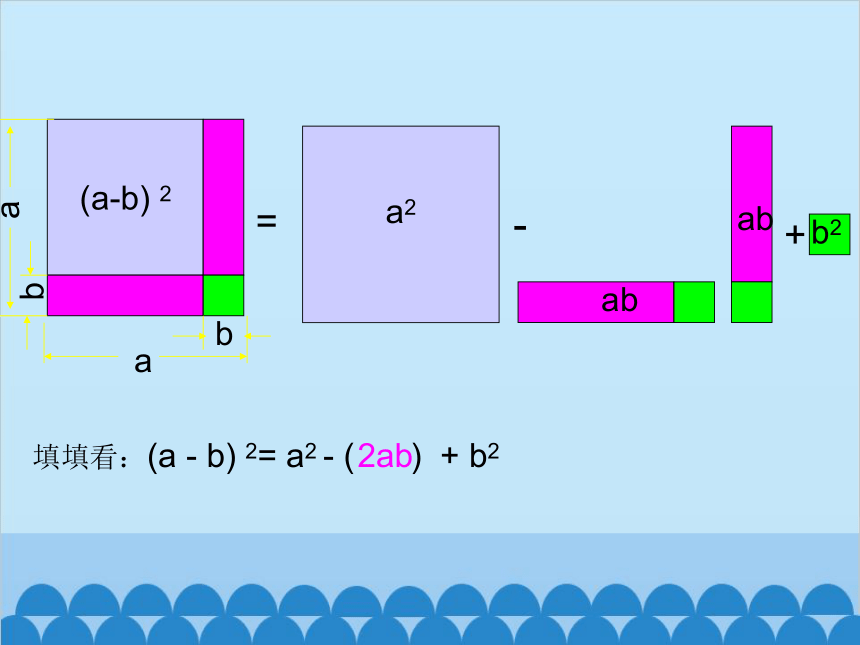
(a-b) 2
填填看:(a - b) 2= a2 - ( ) + b2
2ab
ab
ab
a2
=
b
a
b
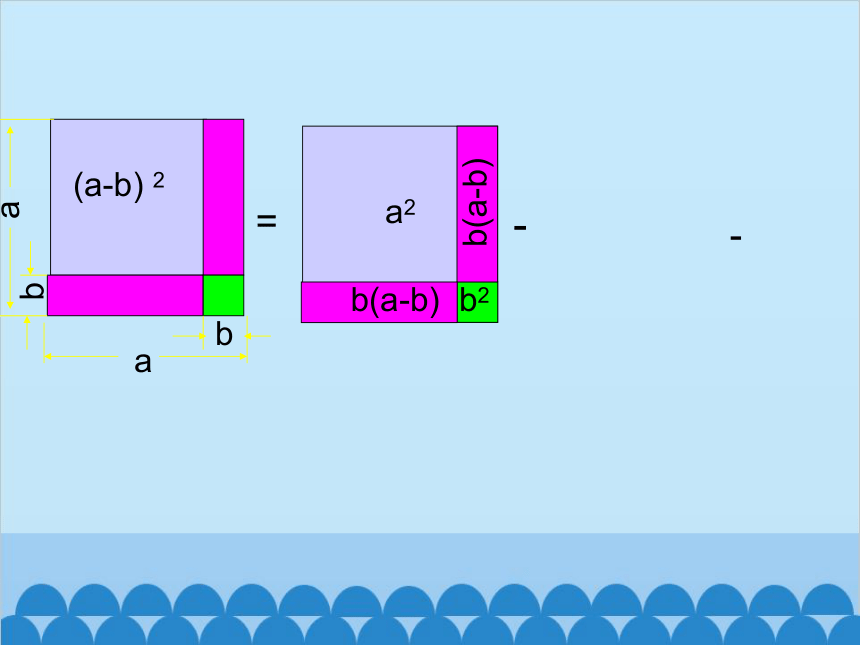
(a-b) 2
a
-
b2
-
b(a-b)
b(a-b)
a
a
b
b
(a+b)(a-b)
=
-
a2
b2
a2
b2
2× (a+b)(a-b)=( )-( )
你能把这三个公式写在下面吗?
请说说每个公式的特征(注意项数和符号)
(a+b)(a-b) =
(a+b) 2 =
(a-b) 2 =
a2+2ab+b2
a 2- b2
a2-2ab+b2
(a±b) 2 =
a2±2ab+b2
四、知识运用
㈠例1 利用乘法公式计算:
⑴ (2x+y) 2
⑵ (3a-2b) 2
⑶ (1-3m)(1+3m)
小小提示:计算前,先看看该用哪个公式,并
识别a、b在具体式子中分别表示什么。
( a + b) 2 = a2 + 2 a b + b2
解:⑴ (2x + y) 2=
(2x)2
+ 2 ·
(2x)
y
+ y2
=4x2+4xy+y2
=9a2-12ab+4b2
( a + b) 2 = a2 + 2 a b + b2
⑵ [3a+(-2b)] 2=
(3a)2
+ 2·
(3a)
(-2b)
+ (-2b)2
如果把这题看成3a与-2b的和,用刚才第小题的公式,你会做吗
( a - b) 2 = a2 - 2 a b + b2
⑵ (3a-2b) 2=
(3a)2
- 2 ·
(3a)
(2b)
+ (2b)2
=9a2-12ab+4b2
⑶ (1 - 3m)(1 + 3m) =
(a - b) (a + b) = a 2- b2
=1-9m2
- (3m)2
1
考考你:
⑴(2a+5b)(2a-5b)
⑶(y-2x)(-2x-y)
⑴(2x+ )2
⑷(-2x+3y)2
小小提示:在具体的题目中,有时题里的a、b代表的项不能
和公式里的a、b 的位置一一对应,你就要善于识别,
以便和公式中的a、b对应起来.
㈡例2:利用乘法公式计算
⑴ 1999×2001
⑵ (x + 3)(x - 3)(x2 + 9)
解:⑴ 1999×2001
= (2000-1)×(2000+1)
= 20002-12
= 3 999 999
⑵ (x + 3)(x - 3)(x2 + 9)
= (x2 - 9)(x2 + 9)
= x4 - 81
五、课堂小结
1、本节课学习了什么知识,你能回忆起来吗?
2、在使用这些公式时要注意什么问题呢?
3、根据例题,谈谈这些公式中字母可以代表哪些东西?
六、课外练兵
P60练习1、2
完全平方公式与平方差公式(1、2)
教学目标:
1、经历探索平方差公式与完全平方公式的发展过程,发展学生观察、交流、归纳、猜测、验证等能力。
2、会推导乘法公式:
,了解公式的几何背景,会用公式计算。
3、进一步体会数形结合的数学思想和方法。
教材分析:
由多项式的乘法到乘法公式是一般到特殊的认识过程,对它的学习丰富了教学内容,开阔了学生的视野,所以乘法公式的应用是本节内容的重点。难点是公式的结构特征及公式中字母所表示的广泛含义的理解和正确运用。
(a±b) 2 =
a2±2ab+b2
(a+b)(a-b) =
a 2- b2
2、你记得多项式乘法法则吗?
多项式与多项式相乘,先用一个多项式的每一项与另一个多项式的每一项相乘,再把所得的积相加.
(a+b)(a-b) =
(a+b) 2 =
(a-b) 2 =
a2+2ab+b2
a 2- b2
a2-2ab+b2
1、你能写出a与b的平方和和a与b和的平方分别是什么吗?
一、复习导入
a 2+b2
(a+b)2
平方差公式
(a+b)(a-b)=
a 2- b2
①
(a+b) 2=
(a-b) 2=
a2+2ab+b2
a2-2ab+b2
②
③
完全平方公式
你能用语言叙述这两个公式吗?
(二)、两个数的和的平方,等于这两个数平方的和与
这两个数的积的2倍的和.
(一)、两个数的和与这两个数的差相乘,等于这两个数的
平方差.
a-b可看成a与-b的和
二、探究新知
三、交流
a
b
a
b
(a+b) 2
a2
b2
+
+
=
填填看:(a + b) 2= a2 + 2ab + ( )
b2
ab
ab
ab
a
a2
b2
+
-
=
b
a
b
(a-b) 2
填填看:(a - b) 2= a2 - ( ) + b2
2ab
ab
ab
a2
=
b
a
b
(a-b) 2
a
-
b2
-
b(a-b)
b(a-b)
a
a
b
b
(a+b)(a-b)
=
-
a2
b2
a2
b2
2× (a+b)(a-b)=( )-( )
你能把这三个公式写在下面吗?
请说说每个公式的特征(注意项数和符号)
(a+b)(a-b) =
(a+b) 2 =
(a-b) 2 =
a2+2ab+b2
a 2- b2
a2-2ab+b2
(a±b) 2 =
a2±2ab+b2
四、知识运用
㈠例1 利用乘法公式计算:
⑴ (2x+y) 2
⑵ (3a-2b) 2
⑶ (1-3m)(1+3m)
小小提示:计算前,先看看该用哪个公式,并
识别a、b在具体式子中分别表示什么。
( a + b) 2 = a2 + 2 a b + b2
解:⑴ (2x + y) 2=
(2x)2
+ 2 ·
(2x)
y
+ y2
=4x2+4xy+y2
=9a2-12ab+4b2
( a + b) 2 = a2 + 2 a b + b2
⑵ [3a+(-2b)] 2=
(3a)2
+ 2·
(3a)
(-2b)
+ (-2b)2
如果把这题看成3a与-2b的和,用刚才第小题的公式,你会做吗
( a - b) 2 = a2 - 2 a b + b2
⑵ (3a-2b) 2=
(3a)2
- 2 ·
(3a)
(2b)
+ (2b)2
=9a2-12ab+4b2
⑶ (1 - 3m)(1 + 3m) =
(a - b) (a + b) = a 2- b2
=1-9m2
- (3m)2
1
考考你:
⑴(2a+5b)(2a-5b)
⑶(y-2x)(-2x-y)
⑴(2x+ )2
⑷(-2x+3y)2
小小提示:在具体的题目中,有时题里的a、b代表的项不能
和公式里的a、b 的位置一一对应,你就要善于识别,
以便和公式中的a、b对应起来.
㈡例2:利用乘法公式计算
⑴ 1999×2001
⑵ (x + 3)(x - 3)(x2 + 9)
解:⑴ 1999×2001
= (2000-1)×(2000+1)
= 20002-12
= 3 999 999
⑵ (x + 3)(x - 3)(x2 + 9)
= (x2 - 9)(x2 + 9)
= x4 - 81
五、课堂小结
1、本节课学习了什么知识,你能回忆起来吗?
2、在使用这些公式时要注意什么问题呢?
3、根据例题,谈谈这些公式中字母可以代表哪些东西?
六、课外练兵
P60练习1、2
