数学高中苏教版选修(2-1)2.5《圆锥曲线的统一定义》课件4
文档属性
| 名称 | 数学高中苏教版选修(2-1)2.5《圆锥曲线的统一定义》课件4 |

|
|
| 格式 | zip | ||
| 文件大小 | 76.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-05 15:59:05 | ||
图片预览






文档简介
课件18张PPT。平面内到两定点F1、F2 距离之差的绝对值等于常数2a (2a< F1F2)的点的轨迹平面内到定点F的距离和到定直线l的距离相等的点的轨迹 平面内到两定点 F1、F2 距离之和等于常数 2a (2a>F1F2)的点的轨迹复习回顾表达式 PF1+PF2=2a(2a>F1F2)1、 椭圆的定义:2 、双曲线的定义: 表达式|PF1-PF2|=2a (2a1 时, 点的轨迹是双曲线.圆锥曲线统一定义: (3)当 e = 1 时, 点的轨迹是抛物线.其中常数e叫做圆锥曲线的离心率,
定点F叫做圆锥曲线的焦点,
定直线l就是该圆锥曲线的准线. (1).求下列曲线的焦点坐标与准线方程:
课前预习(1).求下列曲线的焦点坐标与准线方程:
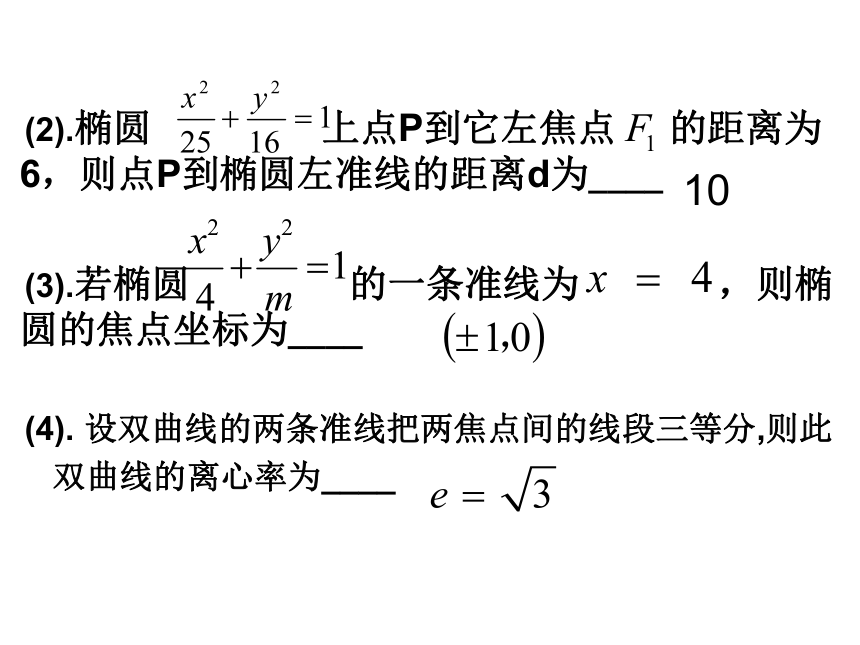
解题反思:焦点与准线的求解:判断曲线的性质→确定焦点的位置→确定a,c,p的值,得出焦点坐标与准线方程.课前预习 (2).椭圆 上点P到它左焦点 的距离为 6,则点P到椭圆左准线的距离d为____
(3).若椭圆 的一条准线为 ,则椭 圆的焦点坐标为____
(4). 设双曲线的两条准线把两焦点间的线段三等分,则此
双曲线的离心率为____
10例1 :已知动点P(x,y) 满足
则P的轨迹是___ 典型例题抛物线 直线 解题反思:紧扣定义,准确判断
1、位置:注意定点是否在直线上
2、顺序:是动点先到定点的距离再与到定直线的距离的比值
3、范围:比值与1的大小比较,准确确定曲线类型。 例2.已知双曲线 上一点P到左焦点的距离为14,求P点到右准线的距离.例2.已知双曲线 上一点P到左焦点
的距离为14,求P点到右准线的距离.解题反思: 2、深刻理解双曲线的两个定义,迅速理
1、位置:判断点P是双曲线的哪一支上清基本量 2、深刻理解双曲线的两个定义,迅速理
2、深刻理解双曲线的两个定义,迅速理
清基本量清基本量 2、深刻理解双曲线的两个定义,迅速理
清基本量 例3.已知点A 为椭圆 内一点,
为其右焦点,M为椭圆上一动点,求(1)
的最小值。MK分析:NAM变题:(2)求 的最大值;分析:解题反思:
1、解决长度和的最值问题要想到圆锥曲线的第一、二定义;
课时练习 5.若点A 的坐标为(3,2),F 为抛
物线 的焦点,点M 在抛物线上
移动时,求MA+MF 的最小值,并求
这时M 的坐标.xyolFAMdN课时小结1.深刻理解圆锥曲线的定义,理清基本量的内在联系2.会用圆锥曲线的定义判断曲线的类型3.会用圆锥曲线的定义、图形解决长度和的最值问题
定点F叫做圆锥曲线的焦点,
定直线l就是该圆锥曲线的准线. (1).求下列曲线的焦点坐标与准线方程:
课前预习(1).求下列曲线的焦点坐标与准线方程:
解题反思:焦点与准线的求解:判断曲线的性质→确定焦点的位置→确定a,c,p的值,得出焦点坐标与准线方程.课前预习 (2).椭圆 上点P到它左焦点 的距离为 6,则点P到椭圆左准线的距离d为____
(3).若椭圆 的一条准线为 ,则椭 圆的焦点坐标为____
(4). 设双曲线的两条准线把两焦点间的线段三等分,则此
双曲线的离心率为____
10例1 :已知动点P(x,y) 满足
则P的轨迹是___ 典型例题抛物线 直线 解题反思:紧扣定义,准确判断
1、位置:注意定点是否在直线上
2、顺序:是动点先到定点的距离再与到定直线的距离的比值
3、范围:比值与1的大小比较,准确确定曲线类型。 例2.已知双曲线 上一点P到左焦点的距离为14,求P点到右准线的距离.例2.已知双曲线 上一点P到左焦点
的距离为14,求P点到右准线的距离.解题反思: 2、深刻理解双曲线的两个定义,迅速理
1、位置:判断点P是双曲线的哪一支上清基本量 2、深刻理解双曲线的两个定义,迅速理
2、深刻理解双曲线的两个定义,迅速理
清基本量清基本量 2、深刻理解双曲线的两个定义,迅速理
清基本量 例3.已知点A 为椭圆 内一点,
为其右焦点,M为椭圆上一动点,求(1)
的最小值。MK分析:NAM变题:(2)求 的最大值;分析:解题反思:
1、解决长度和的最值问题要想到圆锥曲线的第一、二定义;
课时练习 5.若点A 的坐标为(3,2),F 为抛
物线 的焦点,点M 在抛物线上
移动时,求MA+MF 的最小值,并求
这时M 的坐标.xyolFAMdN课时小结1.深刻理解圆锥曲线的定义,理清基本量的内在联系2.会用圆锥曲线的定义判断曲线的类型3.会用圆锥曲线的定义、图形解决长度和的最值问题
