8.3简单几何体的表面积与体积 同步练习(Word版含解析)
文档属性
| 名称 | 8.3简单几何体的表面积与体积 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 07:16:43 | ||
图片预览




文档简介
必修第二册 8.3 简单几何体的表面积与体积
一、单选题
1.已知三棱维中,侧面ABC⊥底面BCD,△ABC是边长为6的正三角形,△BCD是直角三角形,且,则此三棱锥外接球的表面积为( )
A.36π B.48π C.64π D.128π
2.用到球心的距离为1的平面去截球,以所得截面为底面,球心为顶点的圆锥体积为,则球的表面积为( )
A. B. C. D.
3.平行四边形中,,且,沿将四边形折起成平面平面,则三棱锥外接球的表面积为( )
A. B. C. D.
4.三星堆遗址,位于四川省广汉市,距今约三千到五千年.2021年2月4日,在三星堆遗址祭祀坑区4号坑发现了玉琮,玉琮是一种内圆外方的筒型玉器,是一种古人用于祭祀的礼器.假定某玉琮中间内空,形状对称,如图所示,圆筒内径长,外径长,筒高,中部为棱长是的正方体的一部分,圆筒的外侧面内切于正方体的侧面,则该玉琮的体积为( )
A. B. C. D.
5.甲烷是一种有机化合物,分子式为,其在自然界中分布很广,是天然气、沼气的主要成分.如图所示的为甲烷的分子结构模型,已知任意两个氢原子之间的距离(H-H键长)相等,碳原子到四个氢原子的距离(C-H键长)均相等,任意两个H-C-H键之间的夹角为(键角)均相等,且它的余弦值为,即,若,则以这四个氢原子为顶点的四面体的体积为( )
A. B. C. D.
6.已知三棱锥的所有顶点都在球O的球面上,且平面,,,,则球O的表面积为( )
A. B. C. D.
7.正四棱台的上 下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A. B. C. D.
8.已知某圆锥的轴截面是边长为4的正三角形,则它的体积为( ).
A. B. C. D.
9.长方体同一顶点上的三条棱长分别为2,2,3,则长方体的体积与表面积分别为( )
A.12,32 B.12,24 C.22,12 D.12,11
10.据《九章算术》记载,“鳖臑(biēnào)”为四个面都是直角三角形的三棱锥.如图所示,现有一个“鳖臑”,底面,,且,三棱锥外接球表面积为( )
A. B. C. D.
11.已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为
A. B. C. D.
12.棱长为的正方体的外接球的表面积为( )
A. B. C. D.
二、填空题
13.表面积为的球的体积为__________.
14.早期的毕达哥拉斯学派学者注意到:用等边三角形或正方形为表面可构成四种规则的立体图形,即正四面体、正六面体、正八面体和正二十面体,它们的各个面和多面角都全等.如图,正二十面体是由20个等边三角形组成的正多面体,共有12个顶点,30条棱,20个面,是五个柏拉图多面体之一.如果把按计算,则该正二十面体的表面积与该正二十面体的外接球表面积之比等于___________.
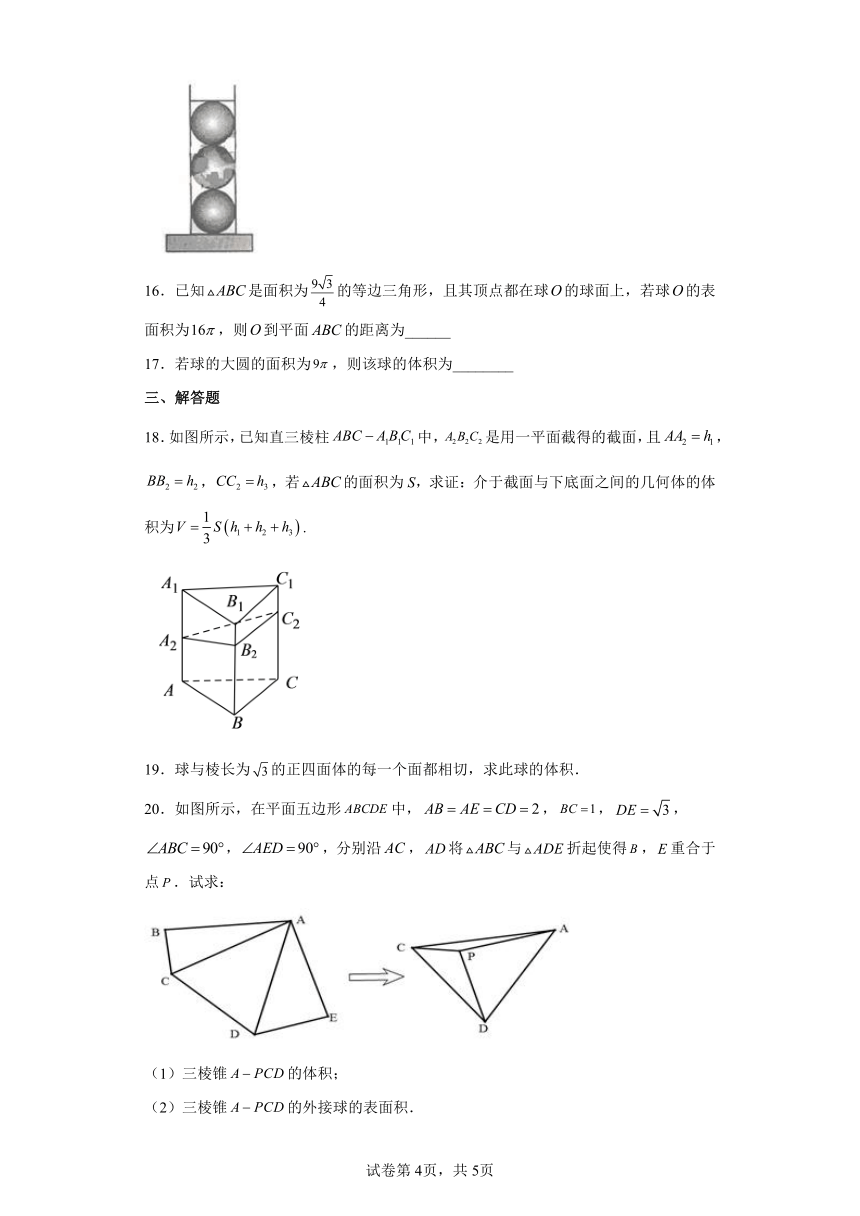
15.圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.
16.已知是面积为的等边三角形,且其顶点都在球的球面上,若球的表面积为,则到平面的距离为______
17.若球的大圆的面积为,则该球的体积为________
三、解答题
18.如图所示,已知直三棱柱中,是用一平面截得的截面,且,,,若的面积为S,求证:介于截面与下底面之间的几何体的体积为.
19.球与棱长为的正四面体的每一个面都相切,求此球的体积.
20.如图所示,在平面五边形中,,,,,,分别沿,将与折起使得,重合于点.试求:
(1)三棱锥的体积;
(2)三棱锥的外接球的表面积.
21.将棱长为的正方体截去三棱锥后得到如图所示几何体,为的中点.
(1)求证:平面;
(2)求几何体的体积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
把三棱锥放置在长方体中,根据长方体的结构特征求出三棱锥外接球的半径,再由三棱锥外接球的表面积公式计算.
【详解】
三棱锥中,侧面底面,把该三棱锥放入长方体中,如图所示
,
设三棱锥外接球的球心为,则,
,
三棱锥外接球的半径,
则三棱锥外接球的表面积为,
故选:C.
2.C
根据球与圆锥的结构特征,结合体积与表面积的计算公式进行求解即可.
【详解】
设球的半径为,圆锥的底面半径为,因为球心到截面的距离为1,
所以有:,
则题中圆锥体积,解得,故球的表面积为.
故选:C
3.C
由平面平面,证得平面和平面,得到、均为,设中点为,连、,根据球的定义,得到为球心,进而求得外接球的表面积为.
【详解】
由题意,平面平面,
又因为平面平面,平面,,可得平面,
因为四边形为平行四边形,所以,
同理平面,所以、均为,
设中点为,连、,
则,其中为三棱锥外接球半径,
则,,
则,故三棱锥外接球的表面积为.
故选:C.
解决与球有关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程:
(1)定球心:如果是内切球,球心到切点的距离相等且为半径;如果是外接球,球心到接点的距离相等且为半径;
(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素间的关系),达到空间问题平面化的目的;
(3)求半径下结论:根据作出截面中的几何元素,建立关于球半径的方程,并求解.
4.A
根据图形,几何体的体积由圆柱的体积加正方体的体积减去正方体遮住圆柱的部分求解.
【详解】
由图可知,组合体的体积为:
,
,
故选:A
5.A
利用余弦定理求得,计算出正四面体的高,从而计算出正四面体的体积.
【详解】
设,则由余弦定理知:,解得,
故该正四面体的棱长均为.
由正弦定理可知:该正四面体底面外接圆的半径,
高.
故该正四面体的体积为.
故选:A
6.A
根据平面BCD,得到,,再由,,,得到,则三棱锥截取于一个长方体,然后由长方体的外接球即为三棱锥的外接球求解.
【详解】
因为平面BCD,
所以,,
∴,
在中,,
∴,
∴.
如图所示:
三棱锥的外接球即为长方体AGFH-BCED的外接球,
设球O的半径为R,则,
解得,
所以球O的表面积为,
故选:A.
7.D
由四棱台的几何特征算出该几何体的高及上下底面面积,再由棱台的体积公式即可得解.
【详解】
作出图形,连接该正四棱台上下底面的中心,如图,
因为该四棱台上下底面边长分别为2,4,侧棱长为2,
所以该棱台的高,
下底面面积,上底面面积,
所以该棱台的体积.
故选:D.
8.C
根据题意,求得圆锥的高和底面圆的半径,代入公式,即可求得答案.
【详解】
如图所示:
为边长为4的正三角形,所以AB=AC=BC=4,
取BC中点为O,则,
所以圆锥的体积.
故选:C
9.A
根据长方体的体积公式和表面积公式可得正确的选项.
【详解】
长方体的体积为,表面积为,
故选:A.
10.C
根据已知条件可将三棱锥补全图形为正方体,可知其外接球为正方体的外接球,即可求外接球表面积.
【详解】
∵底面,,,将三棱锥补全图形为正方体如图所示,
∴三棱锥的外接球即正方体的外接球.
设外接球的半径为,则,解得.
所以外接球的表面积为.
故选:C
本题考查几何体外接球表面积的求法,注意补全三棱锥转化为正方体,应用正方体外接球的性质,属于基础题.
11.B
【详解】
分析:首先根据正方形的面积求得正方形的边长,从而进一步确定圆柱的底面圆半径与圆柱的高,从而利用相关公式求得圆柱的表面积.
详解:根据题意,可得截面是边长为的正方形,
结合圆柱的特征,可知该圆柱的底面为半径是的圆,且高为,
所以其表面积为,故选B.
点睛:该题考查的是有关圆柱的表面积的求解问题,在解题的过程中,需要利用题的条件确定圆柱的相关量,即圆柱的底面圆的半径以及圆柱的高,在求圆柱的表面积的时候,一定要注意是两个底面圆与侧面积的和.
12.C
根据正方体的外接球的直径为正方体的体对角线的长求解.
【详解】
因为正方体的外接球的直径为正方体的体对角线的长,
所以,
解得,
所以球的表面积为:.
故选:C
13.
先求出半径,再利用公式可求体积.
【详解】
,
故答案为:.
14.
可得正二十面体的外接球即为上方正五棱锥的外接球,设外接球半径为R,正五边形的外接圆半径为r,正二十面体的棱长为,可得,,即可表示出外接球的表面积和正二十面体的表面积,得出答案.
【详解】
由图知正二十面体的外接球即为上方正五棱锥的外接球,
设外接球半径为R,正五边形的外接圆半径为r,正二十面体的棱长为,
则,得,
所以正五棱锥的顶点到底面的距离是,
所以,即,解得.
所以该正二十面体的外接球表面积为,
而该正二十面体的表面积是,
所以该正二十面体的表面积与该正二十面体的外接球表面积之比等于.
故答案为:.
本题考查几何体的外接球问题,解题的关键是将正二十面体的外接球等价于上方正五棱锥的外接球,表示出半径.
15.4
【详解】
设球半径为r,则由,
可得,
解得.
【思路点睛】
本题考查几何体的体积,考查学生空间想象能力,解答时,首先设出球的半径,然后再利用三个球的体积和水的体积之和,等于柱体的体积,求解即可.
16.1
画出图形,利用已知条件求三角形的外接圆的半径,然后求解即可.
【详解】
由题意可知图形如图:是面积为的等边三角形,可得,
,
可得:,
球的表面积为,设外接球的半径为;
所以,解得,
所以到平面的距离为:.
故答案为:1.
17.
根据球的大圆的面积,先计算出球的半径,进而可得球的体积.
【详解】
设球的半径为R,
则球的大圆面积为9π=πR2,
解得R=3,
故该球的体积V=πR3=36π,
故答案为36π
本题考查了球的体积公式,面积公式,属于基础题.
18.证明见解析
由于几何体是一个不规则的几何体,为求得其体积,采用分割或补形的方法来求解即可.
【详解】
证法一(分割):为了讨论方便,不妨设.如图所示.
可将几何体分割成一个小直三棱柱与两个三棱锥.
过作交于,过作交于,联结、,
则几何体被分割成:
直三棱柱,三棱锥,三棱锥.
设,A到的距离为d,则,由于
,
,
故.
证法二(补形):将几何体以为底面进行两次等几何体补形,
使侧棱的长均为,这样就将不规则的几何体补形为新的直三棱柱,
而原几何体的体积等于这个新直三棱柱体积的,
故.
19..
在四面体中取面△的中心,连接、,易知可求,进而求正四面体的体积,若内切球半径为,由求,进而求球的体积.
【详解】
如图,在四面体中,取底面△的中心,连接,,则.
又,则.
∴正四面体的体积.
设内切球球心为,半径为,连接,,,.
∴,可得,
∴球的体积.
20.(1);(2).
(1)先判断出三棱锥的高,进而求得三棱锥的体积.
(2)通过补形的方法求得外接球的半径,进而求得外接球的表面积.
【详解】
(1),,,则,
又,,,平面.
所以;
(2)将三棱锥补成长方体知三棱锥的外接球的直径即为长方体的体对角线长,
即,所以球的表面积为.
21.(1)见解析;(2).
(1)取中点为,连接,,,推导出四边形为平行四边形,可得出,再由线面平行的判定可得平面;
(2)由正方体的棱长为2,求得,,,再由体积作差可得几何体的体积.
【详解】
(1)取中点为,连接、、.
在正方形中,为的中点,为的中点.
在正方体中,
且,四边形为平行四边形,且,
、分别为、的中点,且,
所以,四边形为平行四边形,且,
且,且,
所以,四边形为平行四边形,且,
为的中点,且,则四边形为平行四边形,
,
又平面,平面,因此,平面;
(2)∵正方体的棱长为,
,.
又,且,而,
.
本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了利用等体积法求多面体的体积,是中档题.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知三棱维中,侧面ABC⊥底面BCD,△ABC是边长为6的正三角形,△BCD是直角三角形,且,则此三棱锥外接球的表面积为( )
A.36π B.48π C.64π D.128π
2.用到球心的距离为1的平面去截球,以所得截面为底面,球心为顶点的圆锥体积为,则球的表面积为( )
A. B. C. D.
3.平行四边形中,,且,沿将四边形折起成平面平面,则三棱锥外接球的表面积为( )
A. B. C. D.
4.三星堆遗址,位于四川省广汉市,距今约三千到五千年.2021年2月4日,在三星堆遗址祭祀坑区4号坑发现了玉琮,玉琮是一种内圆外方的筒型玉器,是一种古人用于祭祀的礼器.假定某玉琮中间内空,形状对称,如图所示,圆筒内径长,外径长,筒高,中部为棱长是的正方体的一部分,圆筒的外侧面内切于正方体的侧面,则该玉琮的体积为( )
A. B. C. D.
5.甲烷是一种有机化合物,分子式为,其在自然界中分布很广,是天然气、沼气的主要成分.如图所示的为甲烷的分子结构模型,已知任意两个氢原子之间的距离(H-H键长)相等,碳原子到四个氢原子的距离(C-H键长)均相等,任意两个H-C-H键之间的夹角为(键角)均相等,且它的余弦值为,即,若,则以这四个氢原子为顶点的四面体的体积为( )
A. B. C. D.
6.已知三棱锥的所有顶点都在球O的球面上,且平面,,,,则球O的表面积为( )
A. B. C. D.
7.正四棱台的上 下底面的边长分别为2,4,侧棱长为2,则其体积为( )
A. B. C. D.
8.已知某圆锥的轴截面是边长为4的正三角形,则它的体积为( ).
A. B. C. D.
9.长方体同一顶点上的三条棱长分别为2,2,3,则长方体的体积与表面积分别为( )
A.12,32 B.12,24 C.22,12 D.12,11
10.据《九章算术》记载,“鳖臑(biēnào)”为四个面都是直角三角形的三棱锥.如图所示,现有一个“鳖臑”,底面,,且,三棱锥外接球表面积为( )
A. B. C. D.
11.已知圆柱的上、下底面的中心分别为,,过直线的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为
A. B. C. D.
12.棱长为的正方体的外接球的表面积为( )
A. B. C. D.
二、填空题
13.表面积为的球的体积为__________.
14.早期的毕达哥拉斯学派学者注意到:用等边三角形或正方形为表面可构成四种规则的立体图形,即正四面体、正六面体、正八面体和正二十面体,它们的各个面和多面角都全等.如图,正二十面体是由20个等边三角形组成的正多面体,共有12个顶点,30条棱,20个面,是五个柏拉图多面体之一.如果把按计算,则该正二十面体的表面积与该正二十面体的外接球表面积之比等于___________.
15.圆柱形容器内部盛有高度为8cm的水,若放入三个相同的球(球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的球(如图所示),则球的半径是 cm.
16.已知是面积为的等边三角形,且其顶点都在球的球面上,若球的表面积为,则到平面的距离为______
17.若球的大圆的面积为,则该球的体积为________
三、解答题
18.如图所示,已知直三棱柱中,是用一平面截得的截面,且,,,若的面积为S,求证:介于截面与下底面之间的几何体的体积为.
19.球与棱长为的正四面体的每一个面都相切,求此球的体积.
20.如图所示,在平面五边形中,,,,,,分别沿,将与折起使得,重合于点.试求:
(1)三棱锥的体积;
(2)三棱锥的外接球的表面积.
21.将棱长为的正方体截去三棱锥后得到如图所示几何体,为的中点.
(1)求证:平面;
(2)求几何体的体积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.C
把三棱锥放置在长方体中,根据长方体的结构特征求出三棱锥外接球的半径,再由三棱锥外接球的表面积公式计算.
【详解】
三棱锥中,侧面底面,把该三棱锥放入长方体中,如图所示
,
设三棱锥外接球的球心为,则,
,
三棱锥外接球的半径,
则三棱锥外接球的表面积为,
故选:C.
2.C
根据球与圆锥的结构特征,结合体积与表面积的计算公式进行求解即可.
【详解】
设球的半径为,圆锥的底面半径为,因为球心到截面的距离为1,
所以有:,
则题中圆锥体积,解得,故球的表面积为.
故选:C
3.C
由平面平面,证得平面和平面,得到、均为,设中点为,连、,根据球的定义,得到为球心,进而求得外接球的表面积为.
【详解】
由题意,平面平面,
又因为平面平面,平面,,可得平面,
因为四边形为平行四边形,所以,
同理平面,所以、均为,
设中点为,连、,
则,其中为三棱锥外接球半径,
则,,
则,故三棱锥外接球的表面积为.
故选:C.
解决与球有关的切、接问题,其通法是作出截面,将空间几何问题转化为平面几何问题求解,其解题思维流程:
(1)定球心:如果是内切球,球心到切点的距离相等且为半径;如果是外接球,球心到接点的距离相等且为半径;
(2)作截面:选准最佳角度做出截面(要使这个截面尽可能多的包含球、几何体的各种元素以及体现这些元素间的关系),达到空间问题平面化的目的;
(3)求半径下结论:根据作出截面中的几何元素,建立关于球半径的方程,并求解.
4.A
根据图形,几何体的体积由圆柱的体积加正方体的体积减去正方体遮住圆柱的部分求解.
【详解】
由图可知,组合体的体积为:
,
,
故选:A
5.A
利用余弦定理求得,计算出正四面体的高,从而计算出正四面体的体积.
【详解】
设,则由余弦定理知:,解得,
故该正四面体的棱长均为.
由正弦定理可知:该正四面体底面外接圆的半径,
高.
故该正四面体的体积为.
故选:A
6.A
根据平面BCD,得到,,再由,,,得到,则三棱锥截取于一个长方体,然后由长方体的外接球即为三棱锥的外接球求解.
【详解】
因为平面BCD,
所以,,
∴,
在中,,
∴,
∴.
如图所示:
三棱锥的外接球即为长方体AGFH-BCED的外接球,
设球O的半径为R,则,
解得,
所以球O的表面积为,
故选:A.
7.D
由四棱台的几何特征算出该几何体的高及上下底面面积,再由棱台的体积公式即可得解.
【详解】
作出图形,连接该正四棱台上下底面的中心,如图,
因为该四棱台上下底面边长分别为2,4,侧棱长为2,
所以该棱台的高,
下底面面积,上底面面积,
所以该棱台的体积.
故选:D.
8.C
根据题意,求得圆锥的高和底面圆的半径,代入公式,即可求得答案.
【详解】
如图所示:
为边长为4的正三角形,所以AB=AC=BC=4,
取BC中点为O,则,
所以圆锥的体积.
故选:C
9.A
根据长方体的体积公式和表面积公式可得正确的选项.
【详解】
长方体的体积为,表面积为,
故选:A.
10.C
根据已知条件可将三棱锥补全图形为正方体,可知其外接球为正方体的外接球,即可求外接球表面积.
【详解】
∵底面,,,将三棱锥补全图形为正方体如图所示,
∴三棱锥的外接球即正方体的外接球.
设外接球的半径为,则,解得.
所以外接球的表面积为.
故选:C
本题考查几何体外接球表面积的求法,注意补全三棱锥转化为正方体,应用正方体外接球的性质,属于基础题.
11.B
【详解】
分析:首先根据正方形的面积求得正方形的边长,从而进一步确定圆柱的底面圆半径与圆柱的高,从而利用相关公式求得圆柱的表面积.
详解:根据题意,可得截面是边长为的正方形,
结合圆柱的特征,可知该圆柱的底面为半径是的圆,且高为,
所以其表面积为,故选B.
点睛:该题考查的是有关圆柱的表面积的求解问题,在解题的过程中,需要利用题的条件确定圆柱的相关量,即圆柱的底面圆的半径以及圆柱的高,在求圆柱的表面积的时候,一定要注意是两个底面圆与侧面积的和.
12.C
根据正方体的外接球的直径为正方体的体对角线的长求解.
【详解】
因为正方体的外接球的直径为正方体的体对角线的长,
所以,
解得,
所以球的表面积为:.
故选:C
13.
先求出半径,再利用公式可求体积.
【详解】
,
故答案为:.
14.
可得正二十面体的外接球即为上方正五棱锥的外接球,设外接球半径为R,正五边形的外接圆半径为r,正二十面体的棱长为,可得,,即可表示出外接球的表面积和正二十面体的表面积,得出答案.
【详解】
由图知正二十面体的外接球即为上方正五棱锥的外接球,
设外接球半径为R,正五边形的外接圆半径为r,正二十面体的棱长为,
则,得,
所以正五棱锥的顶点到底面的距离是,
所以,即,解得.
所以该正二十面体的外接球表面积为,
而该正二十面体的表面积是,
所以该正二十面体的表面积与该正二十面体的外接球表面积之比等于.
故答案为:.
本题考查几何体的外接球问题,解题的关键是将正二十面体的外接球等价于上方正五棱锥的外接球,表示出半径.
15.4
【详解】
设球半径为r,则由,
可得,
解得.
【思路点睛】
本题考查几何体的体积,考查学生空间想象能力,解答时,首先设出球的半径,然后再利用三个球的体积和水的体积之和,等于柱体的体积,求解即可.
16.1
画出图形,利用已知条件求三角形的外接圆的半径,然后求解即可.
【详解】
由题意可知图形如图:是面积为的等边三角形,可得,
,
可得:,
球的表面积为,设外接球的半径为;
所以,解得,
所以到平面的距离为:.
故答案为:1.
17.
根据球的大圆的面积,先计算出球的半径,进而可得球的体积.
【详解】
设球的半径为R,
则球的大圆面积为9π=πR2,
解得R=3,
故该球的体积V=πR3=36π,
故答案为36π
本题考查了球的体积公式,面积公式,属于基础题.
18.证明见解析
由于几何体是一个不规则的几何体,为求得其体积,采用分割或补形的方法来求解即可.
【详解】
证法一(分割):为了讨论方便,不妨设.如图所示.
可将几何体分割成一个小直三棱柱与两个三棱锥.
过作交于,过作交于,联结、,
则几何体被分割成:
直三棱柱,三棱锥,三棱锥.
设,A到的距离为d,则,由于
,
,
故.
证法二(补形):将几何体以为底面进行两次等几何体补形,
使侧棱的长均为,这样就将不规则的几何体补形为新的直三棱柱,
而原几何体的体积等于这个新直三棱柱体积的,
故.
19..
在四面体中取面△的中心,连接、,易知可求,进而求正四面体的体积,若内切球半径为,由求,进而求球的体积.
【详解】
如图,在四面体中,取底面△的中心,连接,,则.
又,则.
∴正四面体的体积.
设内切球球心为,半径为,连接,,,.
∴,可得,
∴球的体积.
20.(1);(2).
(1)先判断出三棱锥的高,进而求得三棱锥的体积.
(2)通过补形的方法求得外接球的半径,进而求得外接球的表面积.
【详解】
(1),,,则,
又,,,平面.
所以;
(2)将三棱锥补成长方体知三棱锥的外接球的直径即为长方体的体对角线长,
即,所以球的表面积为.
21.(1)见解析;(2).
(1)取中点为,连接,,,推导出四边形为平行四边形,可得出,再由线面平行的判定可得平面;
(2)由正方体的棱长为2,求得,,,再由体积作差可得几何体的体积.
【详解】
(1)取中点为,连接、、.
在正方形中,为的中点,为的中点.
在正方体中,
且,四边形为平行四边形,且,
、分别为、的中点,且,
所以,四边形为平行四边形,且,
且,且,
所以,四边形为平行四边形,且,
为的中点,且,则四边形为平行四边形,
,
又平面,平面,因此,平面;
(2)∵正方体的棱长为,
,.
又,且,而,
.
本题考查直线与平面平行的判定,考查空间想象能力与思维能力,训练了利用等体积法求多面体的体积,是中档题.
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
