10.1随机事件与概率 同步练习(Word版含解析)
文档属性
| 名称 | 10.1随机事件与概率 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 686.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 07:22:48 | ||
图片预览




文档简介
必修第二册 10.1 随机事件与概率 同步练习
一、单选题
1.一个袋子中装有大小形状完全相同的个白球和个黑球,从中一次摸出个球,则摸出白球个数多于黑球个数的概率为( )
A. B. C. D.
2.2021年某省新高考将实行“”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件:“他选择政治和地理”,事件:“他选择化学和地理”,则事件与事件( )
A.是互斥事件,不是对立事件 B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件也不是对立事件
3.某学校计划从名男生和名女生中任选人参加抗疫英雄事迹演讲比赛,记事件为“至少有名女生参加演讲”,则下列事件中与事件对立的是( )
A.恰有名女生参加演讲 B.至多有名男生参加演讲
C.恰有名女生参加演讲 D.至多有名女生参加演讲
4.饕餮(tāo tiè)纹,青铜器上常见的花纹之一,盛行于商代至西周早期,最早出现在距今五千年前长江下游地区的良渚文化玉器上.有人将饕簧纹的一部分画到方格纸上,如图所示,每个小方格的边长为1,有一质点从A点出发跳动五次到达点B,每次向右或向下跳一个单位长度,且向右或向下跳是等可能性的,那么质点跳动的路线恰好在饕餮纹上的概率为( )
A. B. C. D.
5.已知100件产品中有5件次品,从这100件产品中任意取出3件,设表示事件“3件产品 全不是次品”,表示事件“3件产品全是次品”,表示事件“3件产品中至少有1件是 次品”,则下列结论正确的是( )
A.与互斥 B.与互斥但不对立
C.任意两个事件均互斥 D.与对立
6.据《孙子算经》中记载,中国古代诸侯的等级从低到高分为:男 子 伯,侯 公,共五级.若给有巨大贡献的3人进行封爵,假设每种封爵的可能性相等,则3人中恰好有两人被封同一等级的概率为( )
A. B. C. D.
7.已知消费者购买家用小电器有两种方式:网上购买和实体店购买.经工商局抽样调查发现,网上家用小电器合格率约为,而实体店里家用小电器的合格率约为,工商局12315电话接到关于家用小电器不合格的投诉,统计得知,被投诉的是在网上购买的概率约为.那么估计在网上购买家用小电器的人约占( )
A. B. C. D.
8.某地区教研部门为了落实义务教育阶段双减政策,拟出台作业指导方案.在出台方案之前作一个调查,了解本地区义务教育阶段学生中抄袭过作业的学生比例.对随机抽出的2000名学生进行了调查,因问题涉及隐私,调查中使用了两个问题:问题1:你的阳历生日日期是不是偶数?问题2:你是否抄袭过作业?调查者设计了一个随机化装置,这是一个装有除颜色外完全一样的50个白球和50个红球的不透明袋子.每个被调查者随机从袋中摸取1个球,摸出的球看到颜色后放回袋中,只有摸球者自己才能看到摸出球的颜色.要求摸到白球的学生如实回答第一个问题,摸到红球的学生如实回答第二个问题,答案为“是”的人从盒子外的小石子堆中拿一个石子放在盒子中,回答“否”的人什么都不要做.由于问题的答案只有“是”和“否”,而且回答的是哪个问题也是别人不知道的,因此被调查者可以毫无顾虑地给出符合实际情况的答案.调查结果为2000人中共有612人回答“是”,则本地区义务教育阶段学生中抄袭过作业的学生所占百分比最接近( )(提示:假设一年为365天,其中日期为偶数的天数为179天)
A.10.2% B.12.2% C.24.4% D.30.6%
9.斐波那契数列(Fibonacci sequence)又称黄金分割数列,因为数学家昂纳多斐波那契以兔子繁殖为例子引入,故又称为“兔子数列”,在数学上斐波那契数列被以下递推方法定义:数列满足:,,现从该数列的前10项中随机的抽取一项,则该数除以3余数为1的概率为( )
A. B. C. D.
10.素数分布是数论研究的核心领域之一,含有众多著名的猜想.世纪中叶,法国数学家波利尼亚克提出了“广义孪生素数猜想”:对所有自然数,存在无穷多个素数对.其中当时,称为“孪生素数”,时,称为“表兄弟素数”.在不超过的素数中,任选两个不同的素数 (),令事件为孪生素数},为表兄弟素数},,记事件 发生的概率分别为 ,则下列关系式成立的是( )
A.
B.
C.
D.
11.在3张卡片上分别写上3位同学的学号后,再把卡片随机分给这3位同学,每人1张,则恰有1位学生分到写有自己学号卡片的概率为( )
A. B. C. D.
12.已知正六边形的边长为1,在这6个顶点中任意取2个不同的顶点,得到线段,则的概率为( )
A. B. C. D.
二、填空题
13.已知射手甲射击一次,命中9环以上(含9环)的概率为0.5,命中8环的概率为0.2,命中7环的概率为0.1,则甲射击一次,命中6环以下(含6环)的概率为_______.
14.某产品分甲、乙、丙三级,其中甲级属正品,乙、丙两级属次品.若生产中出现乙级产品的概率为0.03,出现丙级产品的概率为0.01,则对成品任意抽查一件抽得正品的概率为__________.
15.若同时掷两颗骰子,则出现两颗骰子的点数之和大于9的概率为________
16.小华 小明 小李 小章去,,,四个工厂参加社会实践,要求每个工厂恰有人去实习,则小华去工厂,且小李没去工厂的概率是___________.
17.已知从某班学生中任选两人参加农场劳动,选中两人都是男生的概率是,选中两人都是女生的概率是,则选中两人中恰有一人是女生的概率为______.
三、解答题
18.掷一枚骰子,给出下列事件:
“出现奇数点”,“出现偶数点”,“出现的点数小于3”.
求:(1),;
(2),.
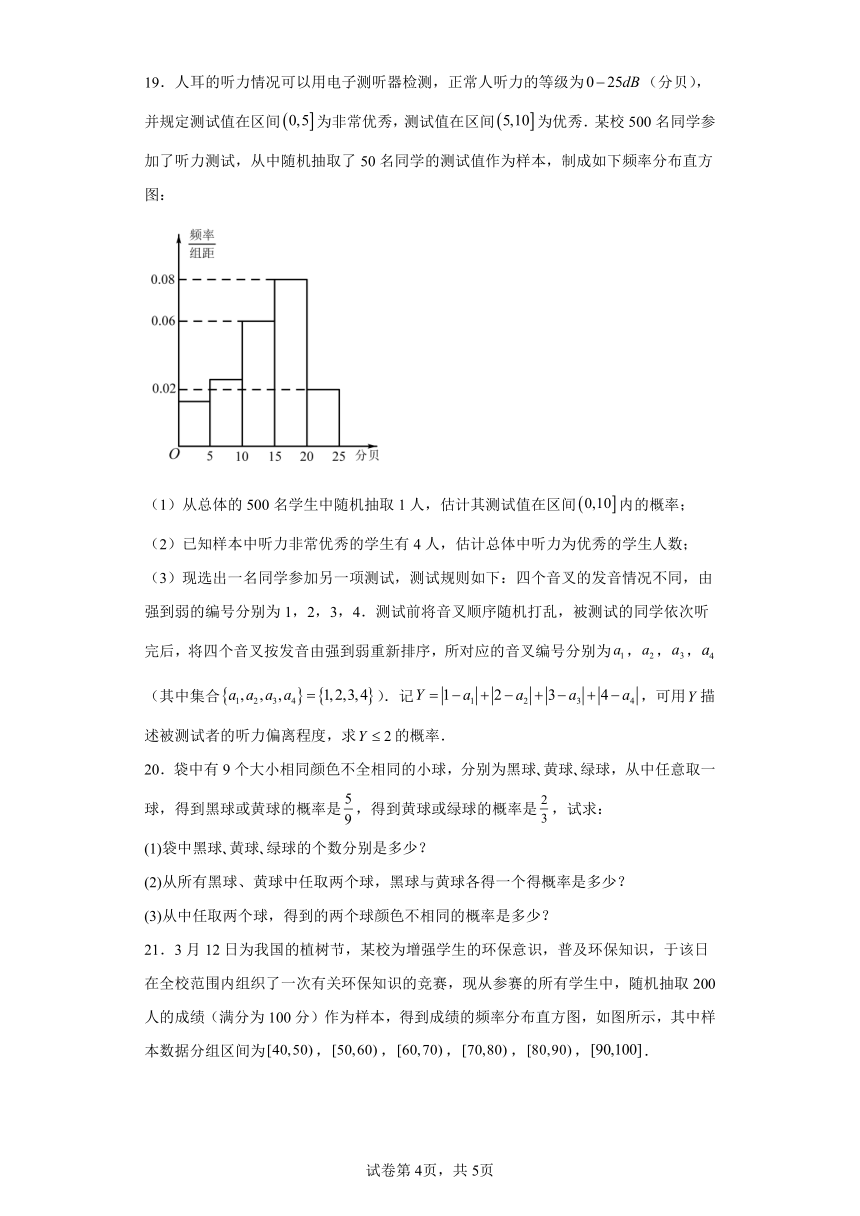
19.人耳的听力情况可以用电子测听器检测,正常人听力的等级为(分贝),并规定测试值在区间为非常优秀,测试值在区间为优秀.某校500名同学参加了听力测试,从中随机抽取了50名同学的测试值作为样本,制成如下频率分布直方图:
(1)从总体的500名学生中随机抽取1人,估计其测试值在区间内的概率;
(2)已知样本中听力非常优秀的学生有4人,估计总体中听力为优秀的学生人数;
(3)现选出一名同学参加另一项测试,测试规则如下:四个音叉的发音情况不同,由强到弱的编号分别为1,2,3,4.测试前将音叉顺序随机打乱,被测试的同学依次听完后,将四个音叉按发音由强到弱重新排序,所对应的音叉编号分别为,,,(其中集合).记,可用描述被测试者的听力偏离程度,求的概率.
20.袋中有9个大小相同颜色不全相同的小球,分别为黑球 黄球 绿球,从中任意取一球,得到黑球或黄球的概率是,得到黄球或绿球的概率是,试求:
(1)袋中黑球 黄球 绿球的个数分别是多少?
(2)从所有黑球、黄球中任取两个球,黑球与黄球各得一个得概率是多少?
(3)从中任取两个球,得到的两个球颜色不相同的概率是多少?
21.3月12日为我国的植树节,某校为增强学生的环保意识,普及环保知识,于该日在全校范围内组织了一次有关环保知识的竞赛,现从参赛的所有学生中,随机抽取200人的成绩(满分为100分)作为样本,得到成绩的频率分布直方图,如图所示,其中样本数据分组区间为,,,,,.
(1)求频率分布直方图中的值,并估计该校此次环保知识竞赛成绩的平均分(同一组中的数据用该组区间中点值为代表);
(2)在该样本中,若采用分层抽样的方法,从成绩低于70分的学生中随机抽取6人,查看他们的答题情况,再从这6人中随机抽取3人进行调查分析,求这3人中至少有1人成绩在内的概率.
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.C
根据古典概型的概念及计算公式直接计算即可.
【详解】
一个袋子中装有大小形状完全相同的个白球和个黑球,从中一次摸出个球,
基本事件总数,
摸出白球个数多于黑球个数包含的基本事件个数,
则摸出白球个数多于黑球个数的概率为,
故选:C.
2.A
事件与事件不能同时发生,是互斥事件,他还可以选择化学和政治,不是对立事件,得到答案.
【详解】
事件与事件不能同时发生,是互斥事件
他还可以选择化学和政治,不是对立事件
故答案选A
本题考查了互斥事件和对立事件,意在考查学生对于互斥事件和对立事件的理解.
3.C
列举出从名男生和名女生中任选人所包含的基本事件,并列举出事件所包含的基本事件,利用对立事件的定义判断可得出结论.
【详解】
从名男生和名女生中任选人,所有的基本事件有“名男生名女生参加演讲”、“名男生名女生参加演讲”、“名女生参加演讲”,
事件所包含的基本事件有“名男生名女生参加演讲”、“名女生参加演讲”,
所以,事件的对立事件为“名男生名女生参加演讲”,即“恰有名女生参加演讲”,
故选:C.
4.D
利用列举法求出基本事件总数和其中恰好是沿着饕餮纹的路线到达的情况的种数,由此能求出恰好是沿着饕餮纹的路线到达的概率.
【详解】
质点从点出发跳动五次到达点,每次向右或向下跳一个单位长度,基本事件总数有:
右右下下下,右下右下下,右下下右下,右下下下右,下右右下下,
下右下右下,下右下下右,下下下右右,下下右右下,下下右下右,共10种,
其中恰好是沿着饕餮纹的路线到达的情况有1种,右右下下下,
恰好是沿着饕餮纹的路线到达的概率为.
故选:D.
5.D
列出基本事件,再结合互斥事件,对立事件的定义即可判断.
【详解】
设1表示取到正品, 0 表示取到次品,所有事件
则
故与不互斥,故A,C错
故与互斥且对立,故B错,D正确
故选:D
6.D
先由题意,确定3人封爵所包含的总的基本事件个数,再求出满足条件的基本事件个数,基本事件个数比,即可为所求概率.
【详解】
由题意,每个人被封爵都有5种情况,因此对3人封爵,共有种,
3人中恰好有两人被封同一等级共有种情况;
则3人中恰好有两人被封同一等级的概率为.
故选:D.
本题主要考查求古典概型的概率,属于常考题型.
7.A
设在网上购买的人数占比为,实体店购买的人数占比为,分别求出各自被投诉的人数的占比,即可求解.
【详解】
设在网上购买的人数占比为,实体店购买的人数占比为,
由题意可得,网上购买的合格率为,
则网上购买被投诉的人数占比为,实体店里购买的被投诉的人数占比为,
所以,解得.
故选:A.
本题主要考查了概率的应用,其中解答中认真审题,求出各自被投诉的人数的占比是解答的关键,着重考查分析问题和解答问题的能力.
8.B
利用概率估计整体,可得回答第一个问题与第二个问题各1000人,再根据偶数天估计第一个问题回答“是”的人数,进而可估计第二个问题回答“是”的人数,可得解.
【详解】
由题意可知,每个学生摸出1个白球或红球的可能性都是,
即大约有1000人回答了第一个问题,另1000人回答了第二个问题,
在摸出白球的情况下,回答“是”的概率为,
所以在回答第一个问题的1000人中,大约有490人回答了“是”,
所以可以推测在回答第二个问题的1000人中,大约有人回答了“是”,
即估计抄袭过作业的学生所占百分比为,
故选:B.
9.D
写出斐波那契数列的前10项,列举出被3除所得的余数,由概率公式可得答案.
【详解】
数列满足:,,
数列的前10项为:1,1,2,3,5,8,13,21,34,55
该数列被3除所得的余数为1,1,2,0,2,2,1,0,1,1
所以10项中共有5项满足除以3余数为1,
故概率为.
故选:D
本题考查概率的求法,考查列举法的应用,属于基础题.
10.D
根据素数的定义,一一列举出不超过的所有素数,共10个,根据组合运算,得出随机选取两个不同的素数、(),有(种)选法,从而可列举出事件、、的所有基本事件,最后根据古典概率分别求出和,从而可得出结果.
【详解】
解:不超过的素数有、、、、、、、、、,共10个,
随机选取两个不同的素数、(),有(种)选法,
事件发生的样本点为、、、共4个,
事件发生的样本点为、、、共4个,
事件发生的样本点为、、、、、
、、、、,共个,
∴,,
故.
故选:D.
关键点点睛:本题考查与素数相关的新定义,考查古典概型的实际应用和利用列举法求古典概型,考查组合数的计算,解题的关键在于理解素数的定义,以及对题目新定义的理解,考查知识运用能力.
11.C
由题意列出所有可能的结果,然后利用古典概型计算公式即可求得满足题意的概率值.
【详解】
设三位同学分别为,他们的学号分别为,
用有序实数列表示三人拿到的卡片种类,如表示同学拿到号,同学拿到号,同学拿到号.
三人可能拿到的卡片结果为:,共6种,
其中满足题意的结果有,共3种,
结合古典概型计算公式可得满足题意的概率值为:.
故选:C.
方法点睛:
有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数.
(1)基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏.
(2)注意区分排列与组合,以及计数原理的正确使用.
12.C
先分析,然后列举基本事件,根据古典概型的概率公式直接求得.
【详解】
由已知得,,,在这6个顶点中任意取2个不同的顶点,,得到以下15条线段:,,,,,,,,,,,,,,,其中满足的有以下6条线段:,,,,,,根据古典概型的计算公式得,的概率为.
故选C.
古典概型的概率计算中列举基本事件的方法:
(1)枚举法;(2)列表法;(3)坐标法;(4)树状图法.
13.0.2
命中6环以下(含6环)的对立事件就是命中七环及以上,根据对立事件关系求解概率.
【详解】
设“命中9环以上(含9环)”为事件A,“命中8环”为事件B,“命中7环”为事件C,“命中6环以下(含6环)”为事件D,
则D与互为对立事件.因为,,,且A,B,C三个事件互斥,
所以,所以.
故答案为:0.2
此题考查互斥事件概率的加法公式,以及通过对立事件的概率关系求解概率.
14.0.96
根据题意,设抽取产品的等级分别为事件、、,且事件,,彼此互斥,根据概率事件加法公式,即可求解.
【详解】
记“抽出的产品为正品”为事件,“抽出的产品为乙级产品”为事件,“抽出的产品为丙级产品”为事件,则事件,,彼此互斥,且与是对立事件,所以.
故答案为:
本题考查对立事件概率公式,属于基础题.
15.
列举基本事件,直接套公式求概率.
【详解】
同时掷两颗骰子,有共36种情况;
而点数之和大于9包括共6种,
所以两颗骰子的点数之和大于9的概率为.
故答案为:.
16.
先列出所有可能的情况,再求出符合条件的情况,再用古典概型的公式求解即可
【详解】
记小华 小明 小李 小章分别为:1、2、3、4,
数组对应A,B,C,D的顺序,
由题意可知总的分配情况有:
,,,,,,
,,,,,,
,,,,,,
,,,,,,
共种,
其中符合条件的情况有:,,,,
共种,故所求概率.
故答案为:
17.
记“选中两人都是男生”为事件,“选中两人都是女生”为事件,“选中两人中恰有一人是女生”为事件,根据为互斥事件,与为对立事件,从而可求出答案.
【详解】
记“选中两人都是男生”为事件,“选中两人都是女生”为事件,“选中两人中恰有一人是女生”为事件,易知为互斥事件,与为对立事件,
又,
所以.
故答案为:.
18.(1),“出现2点”.
(2)“出现1,2,3,4,5或6点”,“出现1,2,4或6点”.
根据题意表示出集合,再求(1),;(2),即可.
【详解】
由题意知:“出现奇数点”,“出现偶数点”,
“出现的点数小于3”,
(1),出现2点”;
(2)“出现1,2,3,4,5或6点”,
“出现1,2,4或6点”.
本题主要考查的是古典概型的基本事件,考查交事件和并事件,需要借助于集合的运算,集合与集合的关系来解决,是基础题.
19.(1)0.2;(2)60;(3).
(1)由频率直方图得到内的频率,由频率即为对应区间的概率即可求区间内的概率;
(2)由(1),结合已知可得样本中听力为优秀的学生人数,由样本中各组人数的比例关系即可估计总体中听力为优秀的学生人数.
(3)由题设,列出所有情况下,,,的组合数量,并写出所有情况的组合数量,应用古典概型求概率即可.
【详解】
(1)根据频率分布直方图知,样本中测试值在区间内的频率为,
以频率为概率,从总体的500名学生中随机抽取1人,估计其测试值在区间内的概率为0.2.
(2)由(1)知:样本中听力为优秀的学生人数为,
∴估计总体中听力为优秀的学生人数为.
(3)当时,序号,,,的情况为6种:
分别记为,,,,,,
同理,当时,序号,,,的情况也分别为6种,
∴序号,,,所有的情况总数为24种.
当时,,,,,
当时,,,,的取值为,,,,
或,,,, 或,,,,
∴时,序号,,,对应的情况为4种,即.
关键点点睛:
(1)应用频率确定指定样本区间中的人员被抽到的概率.
(2)根据样本中指定区间人数的所占比例,估计总体中对应区间的人数.
(3)应用列举法求古典概型的概率.
20.(1)黑球 黄球 绿球的分别有3、2、4个
(2)0.6
(3)
(1)从中任取一球,分别记得到黑球 黄球 绿球为事件,,,由已知列出的方程组,求解可求得,从而可得答案;
(2)由(1)知黑球 黄球个数分别为3,2, 则有从所有黑球、黄球中任取两个球,黑球与黄球各得一个得概率是;
(3)求出从9个球中取出2个球的样本空间中共有的样本点,再求出两个球同色的样本点可得答案.
(1)
解:从中任取一球,分别记得到黑球 黄球 绿球为事件,,,由于,,为互斥事件,
根据已知,得,
解得,
所以,任取一球,得到黑球 黄球 绿球的概率分别是,,.
所以黑球的个数为个,黄球的个数为个,绿球的个数为个,
所以袋中黑球 黄球 绿球的个数分别是3、2、4个.
(2)
解:由(1)知黑球 黄球个数分别为3,2,
所以从所有黑球、黄球中任取两个球,黑球与黄球各得一个得概率是.
(3)
解:从9个球中取出2个球的样本空间中共有36个样本点,
其中两个是黑球的样本点是3个,两个黄球的是1个,两个绿球的是6个,
于是,两个球同色的概率为,
则两个球颜色不相同的概率是.
21.(1),74.7分;(2).
(1)先利用频率和为1求出a,再计算平均数;
(2)利用分层抽样计算人数,利用古典概型的概率公式求概率.
【详解】
解:(1)由频率分布直方图可得,,
解得,
这组样本数据的平均数为,
所以估计该校此次环保知识竞赛成绩的平均分为74.7分;
(2)由频率分布直方图可知,成绩在,,内的频率分别为0.06,0.12,0.18,
所以采用分层抽样的方法从样本中抽取的6人,
成绩在内的有1人,记为A,成绩在内的有2人,记为b、c,成绩在内的有3人,记为1、2、3.
故从成绩在内的6人随机抽取3人,有:Abc、Ab1、Ab2、Ab3、Ac1 、Ac2、Ac3、 A12、 A13、 A23、 bc1、bc2、 bc3、 b12、 b13、 b23、 c12、 c13、 c23、 123,共有20种,
这3人成绩均不在内,有:A12、A13、A23、123,共有4种,
记事件B: 这3人中至少有1人成绩在内
则.
所以这3人中至少有1人成绩在内的概率为.
(1)从频率分布直方图可以估计出的几个数据:
①众数:频率分布直方图中最高矩形的底边中点的横坐标;
②平均数:频率分布直方图每组数值的中间值乘以频率后相加;
③中位数:把频率分布直方图分成两个面积相等部分的平行于y轴的直线横坐标.
(2)古典概型的概率计算中列举基本事件的方法:
①枚举法;②列表法;③坐标法;④树状图法;⑤排列组合求事件个数..
答案第1页,共2页
答案第1页,共2页
一、单选题
1.一个袋子中装有大小形状完全相同的个白球和个黑球,从中一次摸出个球,则摸出白球个数多于黑球个数的概率为( )
A. B. C. D.
2.2021年某省新高考将实行“”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件:“他选择政治和地理”,事件:“他选择化学和地理”,则事件与事件( )
A.是互斥事件,不是对立事件 B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件 D.既不是互斥事件也不是对立事件
3.某学校计划从名男生和名女生中任选人参加抗疫英雄事迹演讲比赛,记事件为“至少有名女生参加演讲”,则下列事件中与事件对立的是( )
A.恰有名女生参加演讲 B.至多有名男生参加演讲
C.恰有名女生参加演讲 D.至多有名女生参加演讲
4.饕餮(tāo tiè)纹,青铜器上常见的花纹之一,盛行于商代至西周早期,最早出现在距今五千年前长江下游地区的良渚文化玉器上.有人将饕簧纹的一部分画到方格纸上,如图所示,每个小方格的边长为1,有一质点从A点出发跳动五次到达点B,每次向右或向下跳一个单位长度,且向右或向下跳是等可能性的,那么质点跳动的路线恰好在饕餮纹上的概率为( )
A. B. C. D.
5.已知100件产品中有5件次品,从这100件产品中任意取出3件,设表示事件“3件产品 全不是次品”,表示事件“3件产品全是次品”,表示事件“3件产品中至少有1件是 次品”,则下列结论正确的是( )
A.与互斥 B.与互斥但不对立
C.任意两个事件均互斥 D.与对立
6.据《孙子算经》中记载,中国古代诸侯的等级从低到高分为:男 子 伯,侯 公,共五级.若给有巨大贡献的3人进行封爵,假设每种封爵的可能性相等,则3人中恰好有两人被封同一等级的概率为( )
A. B. C. D.
7.已知消费者购买家用小电器有两种方式:网上购买和实体店购买.经工商局抽样调查发现,网上家用小电器合格率约为,而实体店里家用小电器的合格率约为,工商局12315电话接到关于家用小电器不合格的投诉,统计得知,被投诉的是在网上购买的概率约为.那么估计在网上购买家用小电器的人约占( )
A. B. C. D.
8.某地区教研部门为了落实义务教育阶段双减政策,拟出台作业指导方案.在出台方案之前作一个调查,了解本地区义务教育阶段学生中抄袭过作业的学生比例.对随机抽出的2000名学生进行了调查,因问题涉及隐私,调查中使用了两个问题:问题1:你的阳历生日日期是不是偶数?问题2:你是否抄袭过作业?调查者设计了一个随机化装置,这是一个装有除颜色外完全一样的50个白球和50个红球的不透明袋子.每个被调查者随机从袋中摸取1个球,摸出的球看到颜色后放回袋中,只有摸球者自己才能看到摸出球的颜色.要求摸到白球的学生如实回答第一个问题,摸到红球的学生如实回答第二个问题,答案为“是”的人从盒子外的小石子堆中拿一个石子放在盒子中,回答“否”的人什么都不要做.由于问题的答案只有“是”和“否”,而且回答的是哪个问题也是别人不知道的,因此被调查者可以毫无顾虑地给出符合实际情况的答案.调查结果为2000人中共有612人回答“是”,则本地区义务教育阶段学生中抄袭过作业的学生所占百分比最接近( )(提示:假设一年为365天,其中日期为偶数的天数为179天)
A.10.2% B.12.2% C.24.4% D.30.6%
9.斐波那契数列(Fibonacci sequence)又称黄金分割数列,因为数学家昂纳多斐波那契以兔子繁殖为例子引入,故又称为“兔子数列”,在数学上斐波那契数列被以下递推方法定义:数列满足:,,现从该数列的前10项中随机的抽取一项,则该数除以3余数为1的概率为( )
A. B. C. D.
10.素数分布是数论研究的核心领域之一,含有众多著名的猜想.世纪中叶,法国数学家波利尼亚克提出了“广义孪生素数猜想”:对所有自然数,存在无穷多个素数对.其中当时,称为“孪生素数”,时,称为“表兄弟素数”.在不超过的素数中,任选两个不同的素数 (),令事件为孪生素数},为表兄弟素数},,记事件 发生的概率分别为 ,则下列关系式成立的是( )
A.
B.
C.
D.
11.在3张卡片上分别写上3位同学的学号后,再把卡片随机分给这3位同学,每人1张,则恰有1位学生分到写有自己学号卡片的概率为( )
A. B. C. D.
12.已知正六边形的边长为1,在这6个顶点中任意取2个不同的顶点,得到线段,则的概率为( )
A. B. C. D.
二、填空题
13.已知射手甲射击一次,命中9环以上(含9环)的概率为0.5,命中8环的概率为0.2,命中7环的概率为0.1,则甲射击一次,命中6环以下(含6环)的概率为_______.
14.某产品分甲、乙、丙三级,其中甲级属正品,乙、丙两级属次品.若生产中出现乙级产品的概率为0.03,出现丙级产品的概率为0.01,则对成品任意抽查一件抽得正品的概率为__________.
15.若同时掷两颗骰子,则出现两颗骰子的点数之和大于9的概率为________
16.小华 小明 小李 小章去,,,四个工厂参加社会实践,要求每个工厂恰有人去实习,则小华去工厂,且小李没去工厂的概率是___________.
17.已知从某班学生中任选两人参加农场劳动,选中两人都是男生的概率是,选中两人都是女生的概率是,则选中两人中恰有一人是女生的概率为______.
三、解答题
18.掷一枚骰子,给出下列事件:
“出现奇数点”,“出现偶数点”,“出现的点数小于3”.
求:(1),;
(2),.
19.人耳的听力情况可以用电子测听器检测,正常人听力的等级为(分贝),并规定测试值在区间为非常优秀,测试值在区间为优秀.某校500名同学参加了听力测试,从中随机抽取了50名同学的测试值作为样本,制成如下频率分布直方图:
(1)从总体的500名学生中随机抽取1人,估计其测试值在区间内的概率;
(2)已知样本中听力非常优秀的学生有4人,估计总体中听力为优秀的学生人数;
(3)现选出一名同学参加另一项测试,测试规则如下:四个音叉的发音情况不同,由强到弱的编号分别为1,2,3,4.测试前将音叉顺序随机打乱,被测试的同学依次听完后,将四个音叉按发音由强到弱重新排序,所对应的音叉编号分别为,,,(其中集合).记,可用描述被测试者的听力偏离程度,求的概率.
20.袋中有9个大小相同颜色不全相同的小球,分别为黑球 黄球 绿球,从中任意取一球,得到黑球或黄球的概率是,得到黄球或绿球的概率是,试求:
(1)袋中黑球 黄球 绿球的个数分别是多少?
(2)从所有黑球、黄球中任取两个球,黑球与黄球各得一个得概率是多少?
(3)从中任取两个球,得到的两个球颜色不相同的概率是多少?
21.3月12日为我国的植树节,某校为增强学生的环保意识,普及环保知识,于该日在全校范围内组织了一次有关环保知识的竞赛,现从参赛的所有学生中,随机抽取200人的成绩(满分为100分)作为样本,得到成绩的频率分布直方图,如图所示,其中样本数据分组区间为,,,,,.
(1)求频率分布直方图中的值,并估计该校此次环保知识竞赛成绩的平均分(同一组中的数据用该组区间中点值为代表);
(2)在该样本中,若采用分层抽样的方法,从成绩低于70分的学生中随机抽取6人,查看他们的答题情况,再从这6人中随机抽取3人进行调查分析,求这3人中至少有1人成绩在内的概率.
试卷第1页,共3页
试卷第2页,共2页
参考答案:
1.C
根据古典概型的概念及计算公式直接计算即可.
【详解】
一个袋子中装有大小形状完全相同的个白球和个黑球,从中一次摸出个球,
基本事件总数,
摸出白球个数多于黑球个数包含的基本事件个数,
则摸出白球个数多于黑球个数的概率为,
故选:C.
2.A
事件与事件不能同时发生,是互斥事件,他还可以选择化学和政治,不是对立事件,得到答案.
【详解】
事件与事件不能同时发生,是互斥事件
他还可以选择化学和政治,不是对立事件
故答案选A
本题考查了互斥事件和对立事件,意在考查学生对于互斥事件和对立事件的理解.
3.C
列举出从名男生和名女生中任选人所包含的基本事件,并列举出事件所包含的基本事件,利用对立事件的定义判断可得出结论.
【详解】
从名男生和名女生中任选人,所有的基本事件有“名男生名女生参加演讲”、“名男生名女生参加演讲”、“名女生参加演讲”,
事件所包含的基本事件有“名男生名女生参加演讲”、“名女生参加演讲”,
所以,事件的对立事件为“名男生名女生参加演讲”,即“恰有名女生参加演讲”,
故选:C.
4.D
利用列举法求出基本事件总数和其中恰好是沿着饕餮纹的路线到达的情况的种数,由此能求出恰好是沿着饕餮纹的路线到达的概率.
【详解】
质点从点出发跳动五次到达点,每次向右或向下跳一个单位长度,基本事件总数有:
右右下下下,右下右下下,右下下右下,右下下下右,下右右下下,
下右下右下,下右下下右,下下下右右,下下右右下,下下右下右,共10种,
其中恰好是沿着饕餮纹的路线到达的情况有1种,右右下下下,
恰好是沿着饕餮纹的路线到达的概率为.
故选:D.
5.D
列出基本事件,再结合互斥事件,对立事件的定义即可判断.
【详解】
设1表示取到正品, 0 表示取到次品,所有事件
则
故与不互斥,故A,C错
故与互斥且对立,故B错,D正确
故选:D
6.D
先由题意,确定3人封爵所包含的总的基本事件个数,再求出满足条件的基本事件个数,基本事件个数比,即可为所求概率.
【详解】
由题意,每个人被封爵都有5种情况,因此对3人封爵,共有种,
3人中恰好有两人被封同一等级共有种情况;
则3人中恰好有两人被封同一等级的概率为.
故选:D.
本题主要考查求古典概型的概率,属于常考题型.
7.A
设在网上购买的人数占比为,实体店购买的人数占比为,分别求出各自被投诉的人数的占比,即可求解.
【详解】
设在网上购买的人数占比为,实体店购买的人数占比为,
由题意可得,网上购买的合格率为,
则网上购买被投诉的人数占比为,实体店里购买的被投诉的人数占比为,
所以,解得.
故选:A.
本题主要考查了概率的应用,其中解答中认真审题,求出各自被投诉的人数的占比是解答的关键,着重考查分析问题和解答问题的能力.
8.B
利用概率估计整体,可得回答第一个问题与第二个问题各1000人,再根据偶数天估计第一个问题回答“是”的人数,进而可估计第二个问题回答“是”的人数,可得解.
【详解】
由题意可知,每个学生摸出1个白球或红球的可能性都是,
即大约有1000人回答了第一个问题,另1000人回答了第二个问题,
在摸出白球的情况下,回答“是”的概率为,
所以在回答第一个问题的1000人中,大约有490人回答了“是”,
所以可以推测在回答第二个问题的1000人中,大约有人回答了“是”,
即估计抄袭过作业的学生所占百分比为,
故选:B.
9.D
写出斐波那契数列的前10项,列举出被3除所得的余数,由概率公式可得答案.
【详解】
数列满足:,,
数列的前10项为:1,1,2,3,5,8,13,21,34,55
该数列被3除所得的余数为1,1,2,0,2,2,1,0,1,1
所以10项中共有5项满足除以3余数为1,
故概率为.
故选:D
本题考查概率的求法,考查列举法的应用,属于基础题.
10.D
根据素数的定义,一一列举出不超过的所有素数,共10个,根据组合运算,得出随机选取两个不同的素数、(),有(种)选法,从而可列举出事件、、的所有基本事件,最后根据古典概率分别求出和,从而可得出结果.
【详解】
解:不超过的素数有、、、、、、、、、,共10个,
随机选取两个不同的素数、(),有(种)选法,
事件发生的样本点为、、、共4个,
事件发生的样本点为、、、共4个,
事件发生的样本点为、、、、、
、、、、,共个,
∴,,
故.
故选:D.
关键点点睛:本题考查与素数相关的新定义,考查古典概型的实际应用和利用列举法求古典概型,考查组合数的计算,解题的关键在于理解素数的定义,以及对题目新定义的理解,考查知识运用能力.
11.C
由题意列出所有可能的结果,然后利用古典概型计算公式即可求得满足题意的概率值.
【详解】
设三位同学分别为,他们的学号分别为,
用有序实数列表示三人拿到的卡片种类,如表示同学拿到号,同学拿到号,同学拿到号.
三人可能拿到的卡片结果为:,共6种,
其中满足题意的结果有,共3种,
结合古典概型计算公式可得满足题意的概率值为:.
故选:C.
方法点睛:
有关古典概型的概率问题,关键是正确求出基本事件总数和所求事件包含的基本事件数.
(1)基本事件总数较少时,用列举法把所有基本事件一一列出时,要做到不重复、不遗漏.
(2)注意区分排列与组合,以及计数原理的正确使用.
12.C
先分析,然后列举基本事件,根据古典概型的概率公式直接求得.
【详解】
由已知得,,,在这6个顶点中任意取2个不同的顶点,,得到以下15条线段:,,,,,,,,,,,,,,,其中满足的有以下6条线段:,,,,,,根据古典概型的计算公式得,的概率为.
故选C.
古典概型的概率计算中列举基本事件的方法:
(1)枚举法;(2)列表法;(3)坐标法;(4)树状图法.
13.0.2
命中6环以下(含6环)的对立事件就是命中七环及以上,根据对立事件关系求解概率.
【详解】
设“命中9环以上(含9环)”为事件A,“命中8环”为事件B,“命中7环”为事件C,“命中6环以下(含6环)”为事件D,
则D与互为对立事件.因为,,,且A,B,C三个事件互斥,
所以,所以.
故答案为:0.2
此题考查互斥事件概率的加法公式,以及通过对立事件的概率关系求解概率.
14.0.96
根据题意,设抽取产品的等级分别为事件、、,且事件,,彼此互斥,根据概率事件加法公式,即可求解.
【详解】
记“抽出的产品为正品”为事件,“抽出的产品为乙级产品”为事件,“抽出的产品为丙级产品”为事件,则事件,,彼此互斥,且与是对立事件,所以.
故答案为:
本题考查对立事件概率公式,属于基础题.
15.
列举基本事件,直接套公式求概率.
【详解】
同时掷两颗骰子,有共36种情况;
而点数之和大于9包括共6种,
所以两颗骰子的点数之和大于9的概率为.
故答案为:.
16.
先列出所有可能的情况,再求出符合条件的情况,再用古典概型的公式求解即可
【详解】
记小华 小明 小李 小章分别为:1、2、3、4,
数组对应A,B,C,D的顺序,
由题意可知总的分配情况有:
,,,,,,
,,,,,,
,,,,,,
,,,,,,
共种,
其中符合条件的情况有:,,,,
共种,故所求概率.
故答案为:
17.
记“选中两人都是男生”为事件,“选中两人都是女生”为事件,“选中两人中恰有一人是女生”为事件,根据为互斥事件,与为对立事件,从而可求出答案.
【详解】
记“选中两人都是男生”为事件,“选中两人都是女生”为事件,“选中两人中恰有一人是女生”为事件,易知为互斥事件,与为对立事件,
又,
所以.
故答案为:.
18.(1),“出现2点”.
(2)“出现1,2,3,4,5或6点”,“出现1,2,4或6点”.
根据题意表示出集合,再求(1),;(2),即可.
【详解】
由题意知:“出现奇数点”,“出现偶数点”,
“出现的点数小于3”,
(1),出现2点”;
(2)“出现1,2,3,4,5或6点”,
“出现1,2,4或6点”.
本题主要考查的是古典概型的基本事件,考查交事件和并事件,需要借助于集合的运算,集合与集合的关系来解决,是基础题.
19.(1)0.2;(2)60;(3).
(1)由频率直方图得到内的频率,由频率即为对应区间的概率即可求区间内的概率;
(2)由(1),结合已知可得样本中听力为优秀的学生人数,由样本中各组人数的比例关系即可估计总体中听力为优秀的学生人数.
(3)由题设,列出所有情况下,,,的组合数量,并写出所有情况的组合数量,应用古典概型求概率即可.
【详解】
(1)根据频率分布直方图知,样本中测试值在区间内的频率为,
以频率为概率,从总体的500名学生中随机抽取1人,估计其测试值在区间内的概率为0.2.
(2)由(1)知:样本中听力为优秀的学生人数为,
∴估计总体中听力为优秀的学生人数为.
(3)当时,序号,,,的情况为6种:
分别记为,,,,,,
同理,当时,序号,,,的情况也分别为6种,
∴序号,,,所有的情况总数为24种.
当时,,,,,
当时,,,,的取值为,,,,
或,,,, 或,,,,
∴时,序号,,,对应的情况为4种,即.
关键点点睛:
(1)应用频率确定指定样本区间中的人员被抽到的概率.
(2)根据样本中指定区间人数的所占比例,估计总体中对应区间的人数.
(3)应用列举法求古典概型的概率.
20.(1)黑球 黄球 绿球的分别有3、2、4个
(2)0.6
(3)
(1)从中任取一球,分别记得到黑球 黄球 绿球为事件,,,由已知列出的方程组,求解可求得,从而可得答案;
(2)由(1)知黑球 黄球个数分别为3,2, 则有从所有黑球、黄球中任取两个球,黑球与黄球各得一个得概率是;
(3)求出从9个球中取出2个球的样本空间中共有的样本点,再求出两个球同色的样本点可得答案.
(1)
解:从中任取一球,分别记得到黑球 黄球 绿球为事件,,,由于,,为互斥事件,
根据已知,得,
解得,
所以,任取一球,得到黑球 黄球 绿球的概率分别是,,.
所以黑球的个数为个,黄球的个数为个,绿球的个数为个,
所以袋中黑球 黄球 绿球的个数分别是3、2、4个.
(2)
解:由(1)知黑球 黄球个数分别为3,2,
所以从所有黑球、黄球中任取两个球,黑球与黄球各得一个得概率是.
(3)
解:从9个球中取出2个球的样本空间中共有36个样本点,
其中两个是黑球的样本点是3个,两个黄球的是1个,两个绿球的是6个,
于是,两个球同色的概率为,
则两个球颜色不相同的概率是.
21.(1),74.7分;(2).
(1)先利用频率和为1求出a,再计算平均数;
(2)利用分层抽样计算人数,利用古典概型的概率公式求概率.
【详解】
解:(1)由频率分布直方图可得,,
解得,
这组样本数据的平均数为,
所以估计该校此次环保知识竞赛成绩的平均分为74.7分;
(2)由频率分布直方图可知,成绩在,,内的频率分别为0.06,0.12,0.18,
所以采用分层抽样的方法从样本中抽取的6人,
成绩在内的有1人,记为A,成绩在内的有2人,记为b、c,成绩在内的有3人,记为1、2、3.
故从成绩在内的6人随机抽取3人,有:Abc、Ab1、Ab2、Ab3、Ac1 、Ac2、Ac3、 A12、 A13、 A23、 bc1、bc2、 bc3、 b12、 b13、 b23、 c12、 c13、 c23、 123,共有20种,
这3人成绩均不在内,有:A12、A13、A23、123,共有4种,
记事件B: 这3人中至少有1人成绩在内
则.
所以这3人中至少有1人成绩在内的概率为.
(1)从频率分布直方图可以估计出的几个数据:
①众数:频率分布直方图中最高矩形的底边中点的横坐标;
②平均数:频率分布直方图每组数值的中间值乘以频率后相加;
③中位数:把频率分布直方图分成两个面积相等部分的平行于y轴的直线横坐标.
(2)古典概型的概率计算中列举基本事件的方法:
①枚举法;②列表法;③坐标法;④树状图法;⑤排列组合求事件个数..
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
