数学高中苏教版选修(2-1)2.2《椭圆》课件
文档属性
| 名称 | 数学高中苏教版选修(2-1)2.2《椭圆》课件 |  | |
| 格式 | zip | ||
| 文件大小 | 90.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-05 15:59:05 | ||
图片预览




文档简介
课件19张PPT。曲线与方程椭圆椭圆椭圆椭圆椭圆椭圆椭圆的定义
椭圆的方程
椭圆的几何性质内容提要练习例题椭圆复习课一、明确目标:
(1)掌握椭圆的两个定义、方程、几何性质(知识目标);
(2)深刻理解掌握椭圆有关概念,应用椭圆的定义、方程、性质来解释问题;
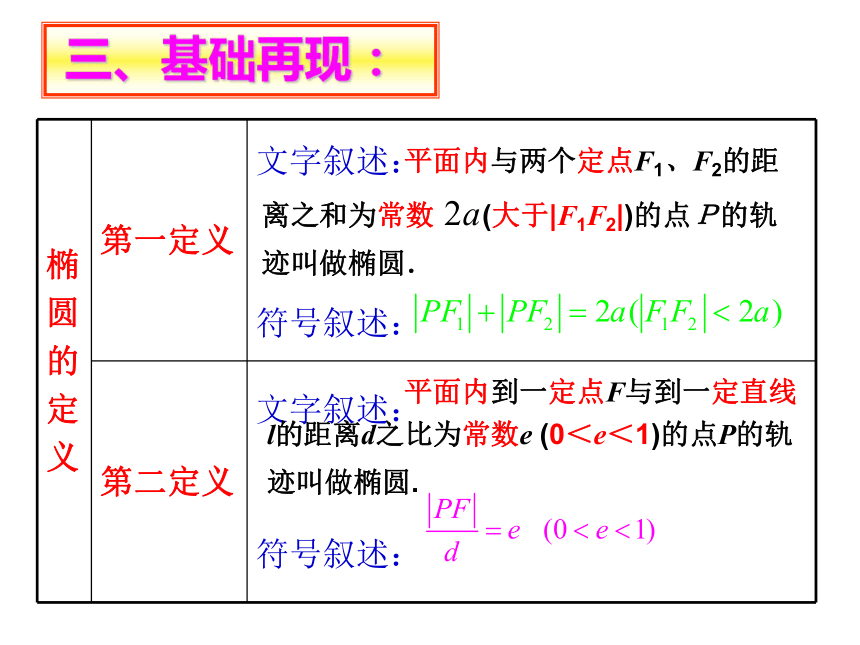
(3)通过复习练习,培养分析问题、解决问题的能力,相互探讨,共同提高。问题:观察下图,请你能说说
我们所学过的椭圆哪些知识?二、问题情境: 三、基础再现:关于x 轴、y 轴和原点对称关于x 轴、y 轴和原点对称xxyyooF1F1F2F2abc 1.已知椭圆上 一点M。
(1)若点M的坐标是(4 , 2.4),则点M与椭圆两个焦点的距离分别是 , ;
(2)若点M到椭圆的一个焦点的距离为3,则
它到相应准线的距离等于 ;
到另一个焦点的距离等于 。577.42.6四、回味无穷(小吃):2、如果方程x2+my2=2表示焦点在y轴的椭圆,那么实数m的取值范围是( )
A(0,+∞) B(-1,0) C(1,+∞) D(0,1)D变式:如果方程x2+my2=2表示椭圆,那么实数m的取值范围是________________-B3.底面直径为12cm的圆柱被与
底面成 的平面所截,截口是
一个椭圆,该椭圆的长轴长
为 ,短轴长为 ,
离心率为 .4 设椭圆的两个焦点分别为F1、、F2,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率是( )
(A) (B) (C) (D)D例1:中心在坐标原点,关于两坐标轴对称的椭圆过点(1,4)、(7,2),求椭圆方程。五、小试牛刀 (知识运用): (2)已知椭圆的中心在原点,焦点在坐标轴上,长轴长是短轴长的3倍,且过点 ,求椭圆的方程; 解:设椭圆的方程的短轴为b,则长轴为3b,依题意得:解得:b= 有同学作如下解答,你认为对吗?若不对,错在哪?应怎样改正。解:以AB的中点O为原点,AB所在直线为x轴建立
直角坐标系.
∵|PA|+|PB|=|PA|+|PM|=|MA|=4又|AB|=2,∴点P在以A,B为焦点的椭圆上,
且a=2,c=1,b=∴点P的轨迹方程为=1.(3)设A、B是两个定点,且 ,
动点M到A点的距离是4,线段MB的垂
直平分线l 交MA于点P,试建立适当的
坐标系,求动点P的轨迹方程.|PA|+|PB|=|PA|+|PM|=|MA|=4=定长【点评】
1.求椭圆方程的基本方法: ①待定系数法; ②利用定义。2.求椭圆方程的基本步骤: ①定型; ②定位; ③定量。3.注意点:建立直角坐标系的原则是:①对称; ②简化。一览众山小(解题总结):例2、已知椭圆椭圆C的左焦点,P为椭圆C上的动点,求的最小值是_________。内有一点A(2,1),F是变式:已知椭圆椭圆C的左焦点,P为椭圆C上的动点,求的最小值与最大值分别是________________。内有一点A(2,1),F是点评:在研究椭圆上的点到焦点距离问题时,能及时返回定义,会事半功倍。是椭圆的一个焦点,则|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|= 。如图,把椭圆的长轴分成等份,过每个分点作半部分于P1,P2,P3,P4,P5,P6,P7七个点,轴的垂线交椭圆的上35(06年川卷理第15题 )六、庖丁解牛 (感受高考)【解法1】 设的对称性,得根据椭圆定义,得:分别是椭圆的左、右焦点,由椭圆图形【解法2】 设F为椭圆的左焦点(c ,0),则有|PF|=a+ex 于是有
|P1F|+|P2F|+…+|P7F|
=(a+ex1)+(a+ex2)+…+(a+ex7)
=7a+e(x1+x2+…+x7)
=7a=35F2【思考2】 显然,P1,P7,…,P5的横坐标x1,x7;x2,x6;x3,x5;分别关于原点对称,P4在y轴上,故有x1+x2+…+x7=0 于是考虑到椭圆的焦半径公式.1. 本节课复习了椭圆的定义、标准方程、简单的几何性质;(应熟练掌握)2.求椭圆方程的基本方法: ①待定系数法; ②利用定义。3.求椭圆方程的基本步骤: ①定型; ②定位; ③定量。4.注意分类讨论、数形结合、函数、方程与不等式等数学思想在解析几何中的应用;七、一吐为快(小结)
椭圆的方程
椭圆的几何性质内容提要练习例题椭圆复习课一、明确目标:
(1)掌握椭圆的两个定义、方程、几何性质(知识目标);
(2)深刻理解掌握椭圆有关概念,应用椭圆的定义、方程、性质来解释问题;
(3)通过复习练习,培养分析问题、解决问题的能力,相互探讨,共同提高。问题:观察下图,请你能说说
我们所学过的椭圆哪些知识?二、问题情境: 三、基础再现:关于x 轴、y 轴和原点对称关于x 轴、y 轴和原点对称xxyyooF1F1F2F2abc 1.已知椭圆上 一点M。
(1)若点M的坐标是(4 , 2.4),则点M与椭圆两个焦点的距离分别是 , ;
(2)若点M到椭圆的一个焦点的距离为3,则
它到相应准线的距离等于 ;
到另一个焦点的距离等于 。577.42.6四、回味无穷(小吃):2、如果方程x2+my2=2表示焦点在y轴的椭圆,那么实数m的取值范围是( )
A(0,+∞) B(-1,0) C(1,+∞) D(0,1)D变式:如果方程x2+my2=2表示椭圆,那么实数m的取值范围是________________-B3.底面直径为12cm的圆柱被与
底面成 的平面所截,截口是
一个椭圆,该椭圆的长轴长
为 ,短轴长为 ,
离心率为 .4 设椭圆的两个焦点分别为F1、、F2,过F2作椭圆长轴的垂线交椭圆于点P,若△F1PF2为等腰直角三角形,则椭圆的离心率是( )
(A) (B) (C) (D)D例1:中心在坐标原点,关于两坐标轴对称的椭圆过点(1,4)、(7,2),求椭圆方程。五、小试牛刀 (知识运用): (2)已知椭圆的中心在原点,焦点在坐标轴上,长轴长是短轴长的3倍,且过点 ,求椭圆的方程; 解:设椭圆的方程的短轴为b,则长轴为3b,依题意得:解得:b= 有同学作如下解答,你认为对吗?若不对,错在哪?应怎样改正。解:以AB的中点O为原点,AB所在直线为x轴建立
直角坐标系.
∵|PA|+|PB|=|PA|+|PM|=|MA|=4又|AB|=2,∴点P在以A,B为焦点的椭圆上,
且a=2,c=1,b=∴点P的轨迹方程为=1.(3)设A、B是两个定点,且 ,
动点M到A点的距离是4,线段MB的垂
直平分线l 交MA于点P,试建立适当的
坐标系,求动点P的轨迹方程.|PA|+|PB|=|PA|+|PM|=|MA|=4=定长【点评】
1.求椭圆方程的基本方法: ①待定系数法; ②利用定义。2.求椭圆方程的基本步骤: ①定型; ②定位; ③定量。3.注意点:建立直角坐标系的原则是:①对称; ②简化。一览众山小(解题总结):例2、已知椭圆椭圆C的左焦点,P为椭圆C上的动点,求的最小值是_________。内有一点A(2,1),F是变式:已知椭圆椭圆C的左焦点,P为椭圆C上的动点,求的最小值与最大值分别是________________。内有一点A(2,1),F是点评:在研究椭圆上的点到焦点距离问题时,能及时返回定义,会事半功倍。是椭圆的一个焦点,则|P1F|+|P2F|+|P3F|+|P4F|+|P5F|+|P6F|+|P7F|= 。如图,把椭圆的长轴分成等份,过每个分点作半部分于P1,P2,P3,P4,P5,P6,P7七个点,轴的垂线交椭圆的上35(06年川卷理第15题 )六、庖丁解牛 (感受高考)【解法1】 设的对称性,得根据椭圆定义,得:分别是椭圆的左、右焦点,由椭圆图形【解法2】 设F为椭圆的左焦点(c ,0),则有|PF|=a+ex 于是有
|P1F|+|P2F|+…+|P7F|
=(a+ex1)+(a+ex2)+…+(a+ex7)
=7a+e(x1+x2+…+x7)
=7a=35F2【思考2】 显然,P1,P7,…,P5的横坐标x1,x7;x2,x6;x3,x5;分别关于原点对称,P4在y轴上,故有x1+x2+…+x7=0 于是考虑到椭圆的焦半径公式.1. 本节课复习了椭圆的定义、标准方程、简单的几何性质;(应熟练掌握)2.求椭圆方程的基本方法: ①待定系数法; ②利用定义。3.求椭圆方程的基本步骤: ①定型; ②定位; ③定量。4.注意分类讨论、数形结合、函数、方程与不等式等数学思想在解析几何中的应用;七、一吐为快(小结)
