数学高中苏教版选修(2-1)2.3《双曲线》课件
文档属性
| 名称 | 数学高中苏教版选修(2-1)2.3《双曲线》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 213.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-05 15:59:05 | ||
图片预览





文档简介
课件17张PPT。 双曲线
的简单几何性质双曲线的标准方程形式一:
(焦点在x轴上,(-c,0)、 (c,0)) 形式二:
(焦点在y轴上,(0,-c)、(0,c))
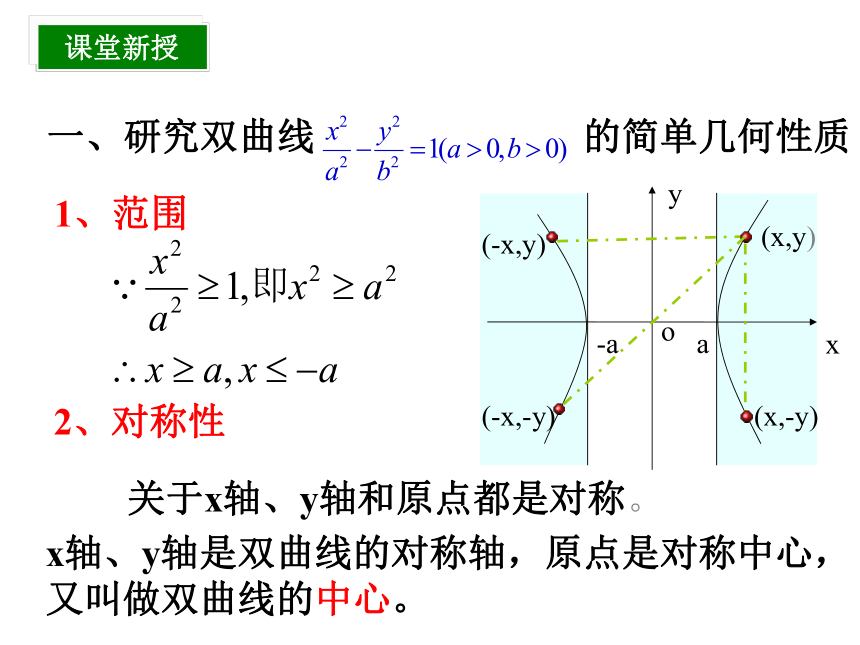
其中复 习 2、对称性 一、研究双曲线 的简单几何性质1、范围关于x轴、y轴和原点都是对称。x轴、y轴是双曲线的对称轴,原点是对称中心,
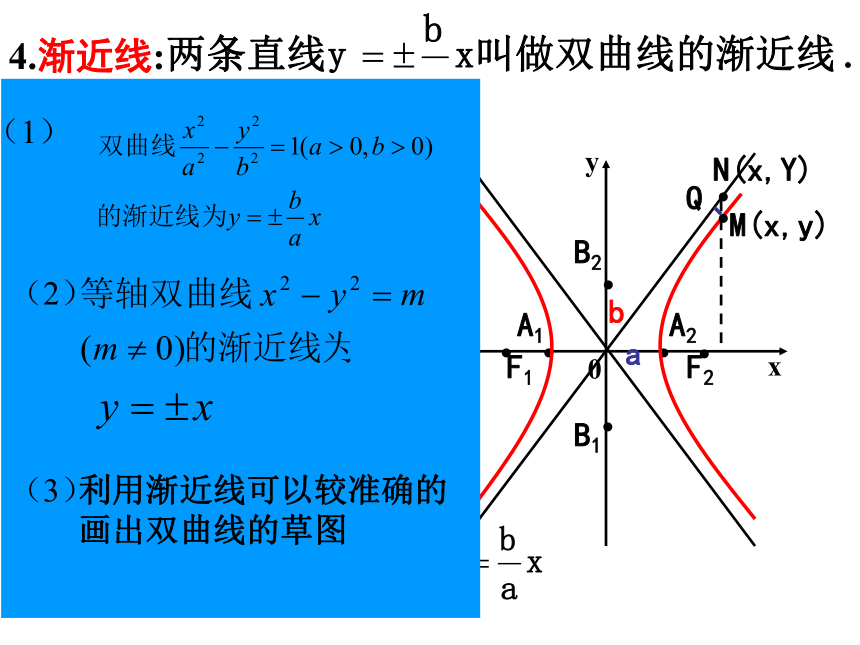
又叫做双曲线的中心。(-x,-y)(-x,y)(x,y)(x,-y)课堂新授 3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点F1F20xyA1A2B2B1baN(x,Y)M(x,y)QF1F20xyA1A2B2B1baN(x,Y)M(x,y)Q4.渐近线:5、离心率离心率。c>a>0e >1e是表示双曲线开口大小的一个量,e越大开口越大(1)定义:(2)e的范围:(3)e的含义:(1)范围:(4)渐近线:(5)离心率:小 结或或关于坐标
轴和
原点
都对
称例1 :求双曲线的实半轴长,虚半轴长,焦点坐标,离心率.渐近线方程。解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3半焦距c=
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:例题讲解 1、填表|x|≥618|x|≥3(±3,0)y=±3x44|y|≥2(0,±2)1014|y|≥5(0,±5)返回课堂练习1一、椭圆与双曲线的比较小 结|x|?a,|y|≤b|x| ≥ a,y?R对称轴:x轴,y轴
对称中心:原点对称轴:x轴,y轴
对称中心:原点(-a,0) (a,0)
(0,b) (0,-b)
长轴:2a 短轴:2b(-a,0) (a,0)
实轴:2a
虚轴:2b无二、根据双曲线的标准方程写出渐进线的方法方法一:画以实轴长、虚轴长为邻边的矩形,写出其对角线方程,
特别注意对角线斜率的确定。方法二:将双曲线标准方程等号右边的1改为0,即得双曲线的渐进线方程,据此得y=kx的形式。返回课外作业:再见!
的简单几何性质双曲线的标准方程形式一:
(焦点在x轴上,(-c,0)、 (c,0)) 形式二:
(焦点在y轴上,(0,-c)、(0,c))
其中复 习 2、对称性 一、研究双曲线 的简单几何性质1、范围关于x轴、y轴和原点都是对称。x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。(-x,-y)(-x,y)(x,y)(x,-y)课堂新授 3、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点F1F20xyA1A2B2B1baN(x,Y)M(x,y)QF1F20xyA1A2B2B1baN(x,Y)M(x,y)Q4.渐近线:5、离心率离心率。c>a>0e >1e是表示双曲线开口大小的一个量,e越大开口越大(1)定义:(2)e的范围:(3)e的含义:(1)范围:(4)渐近线:(5)离心率:小 结或或关于坐标
轴和
原点
都对
称例1 :求双曲线的实半轴长,虚半轴长,焦点坐标,离心率.渐近线方程。解:把方程化为标准方程可得:实半轴长a=4虚半轴长b=3半焦距c=
焦点坐标是(0,-5),(0,5)离心率:渐近线方程:例题讲解 1、填表|x|≥618|x|≥3(±3,0)y=±3x44|y|≥2(0,±2)1014|y|≥5(0,±5)返回课堂练习1一、椭圆与双曲线的比较小 结|x|?a,|y|≤b|x| ≥ a,y?R对称轴:x轴,y轴
对称中心:原点对称轴:x轴,y轴
对称中心:原点(-a,0) (a,0)
(0,b) (0,-b)
长轴:2a 短轴:2b(-a,0) (a,0)
实轴:2a
虚轴:2b无二、根据双曲线的标准方程写出渐进线的方法方法一:画以实轴长、虚轴长为邻边的矩形,写出其对角线方程,
特别注意对角线斜率的确定。方法二:将双曲线标准方程等号右边的1改为0,即得双曲线的渐进线方程,据此得y=kx的形式。返回课外作业:再见!
