数学高中苏教版选修(2-1)2.1《圆锥曲线》课件1
文档属性
| 名称 | 数学高中苏教版选修(2-1)2.1《圆锥曲线》课件1 |

|
|
| 格式 | zip | ||
| 文件大小 | 195.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-05 00:00:00 | ||
图片预览






文档简介
课件20张PPT。高中数学 选修2-12.1 圆锥曲线
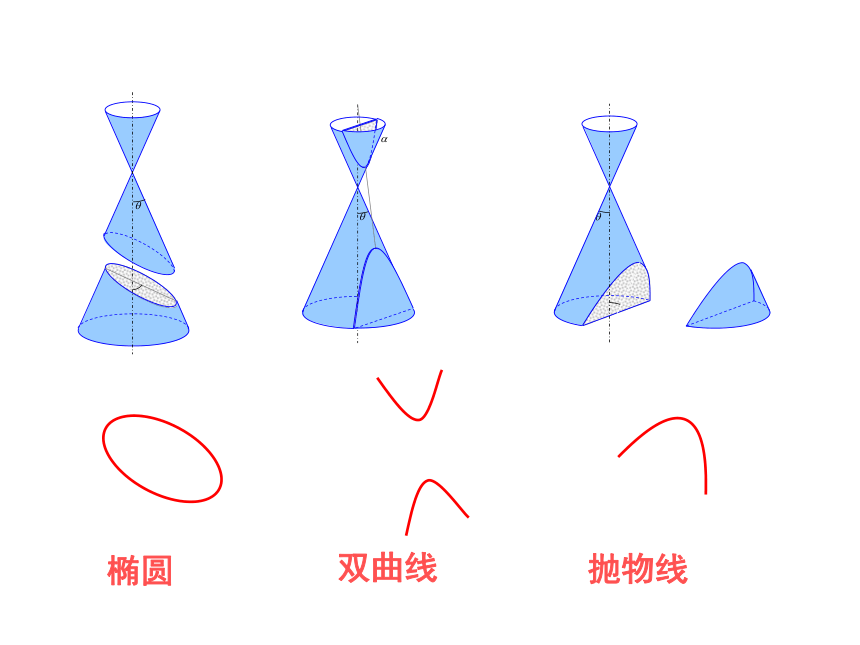
用一个平面去截一个圆锥面,当平面经过圆锥面的顶点时,可得到两条相交直线; 当平面与圆锥面的轴垂直时,截线(平面与圆锥面的交线)是一个圆. 当改变截面与圆锥面的轴的相对位置时,观察截线的变化情况,并思考:
用平面截圆锥面还能得到哪些曲线?这些曲线具有哪些几何特征?
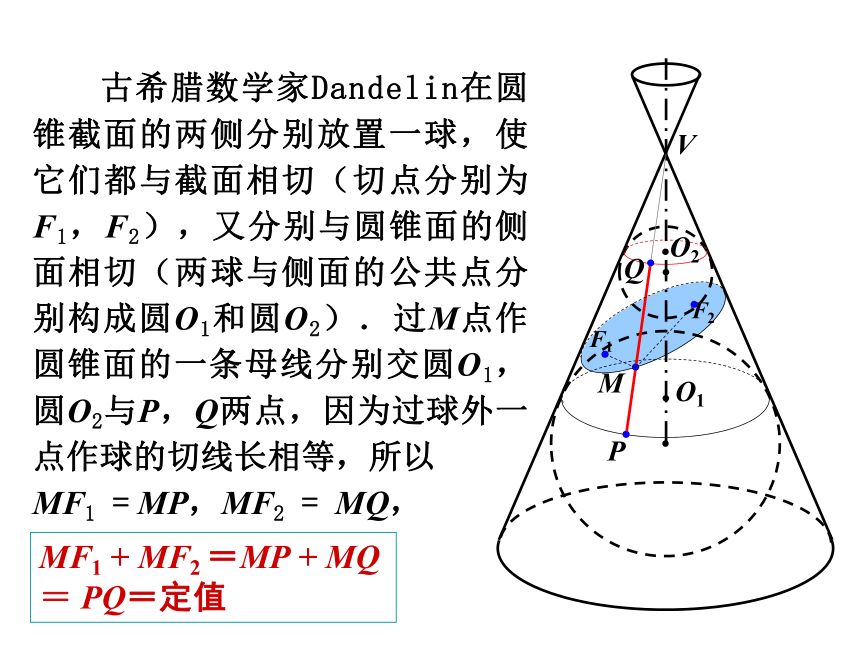
椭圆双曲线抛物线椭圆的定义 平面内到两定点F1 ,F2的距离之和为常数(大于F1 F2距离)的点的轨迹叫椭圆,两个定点叫椭圆的焦点,两焦点的距离叫做椭圆的焦距. 古希腊数学家Dandelin在圆锥截面的两侧分别放置一球,使它们都与截面相切(切点分别为F1,F2),又分别与圆锥面的侧面相切(两球与侧面的公共点分别构成圆O1和圆O2).过M点作圆锥面的一条母线分别交圆O1,圆O2与P,Q两点,因为过球外一点作球的切线长相等,所以
MF1 = MP,MF2 = MQ, MF1 + MF2 =MP + MQ = PQ=定值 F1双曲线的定义 平面内到两个定点F1,F2的距离的差的绝对值等于常数(小于 距离)的点的轨迹叫做双曲线,两个定点F1 , F2叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
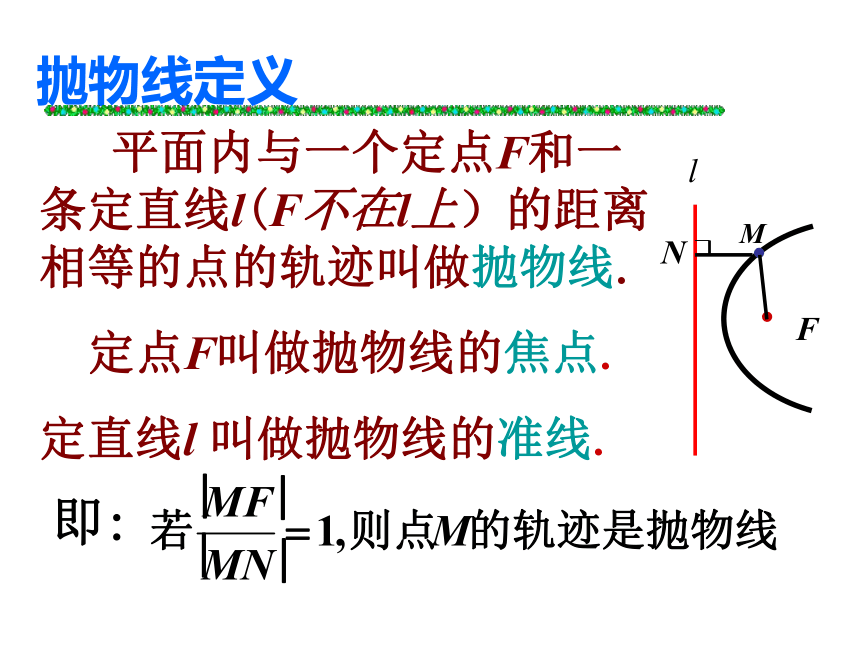
平面内与一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线.
定点F叫做抛物线的焦点.
定直线l 叫做抛物线的准线. 抛物线定义 椭圆的定义: 可以用数学表达式来体现: 设平面内的动点为M,有
(2a> 的常数)
思考:
在椭圆的定义中,如果这个常数小于或等于 ,动点M的轨迹又如何呢? 平面内到两定点F1,F2的距离和等于常数(大于F1F2)的点的轨迹叫做椭圆,两个定点F1,F2叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.双曲线的定义: 平面内到两定点 F1,F2的距离的差的绝对值等于常数(小于F1F2 )的点的轨迹叫做双曲线,两个定点F1,F2叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
可以用数学表达式来体现:设平面内的动点为M,有
(0<2a< 的常数)
思考:
在双曲线的定义中,如果这个常数大于或等于 ,动点M的轨迹又如何呢? 抛物线的定义 : 平面内到一个定点F和一条定直线l(F不在l 上)的距离相等的点轨迹叫做抛物线,定点F叫做抛物线的焦点,定直线l叫做抛物线的准线. 设平面内的动点为M ,有MF=d(d为动点M到直线l的距离). 可以用数学表达式来体现:说明: 1.椭圆、双曲线、抛物线统称为圆锥曲线. 2.我们可利用上面的三条关系式来判断动点M的轨迹是什么. 例1,已知三角形ABC中,B(-3,0),C(3,0),且AB,BC,AC成等差数列。
(1)求证:点A在一个椭圆上运动。
(2)写出这个椭圆的焦点坐标。证:(1)根据条件有AB+AC=2BC,
即AB+AC= 12,
即动点A到定点B,C的距离之和为定值12,
且12>6=BC,所以点A在以B,C为焦点的一个椭圆上运动.
(2)B,C即为椭圆的焦点,所以焦点坐标为(-3,0),(3,0)例2 动圆M过定圆C外的一点A,且与圆C外切,问:动圆圆心M的轨迹是什么图形?AMC变题:若动圆M过点A且与圆C 相切呢?例3 已知定点F和定直线l,F不在直线l上,动圆M过F点且与直线l相切,求证:圆心M的轨迹是一条抛物线.分析:欲证明轨迹为抛物线只需抓住抛物线的定义即可. 1.平面内到两定点F1(-4,0)、F2(4,0)的距离和等于10的点的轨迹是 ( )
A. 椭圆 B.双曲线 C. 抛物线 D.线段2.平面内到两定点F1(-1,0)、F2 (1,0)的距离的差的绝对值等于2的点的轨迹是 ( )
A. 椭圆 B.双曲线 C.线段 D.两条射线 课堂练习4.平面内到点F (0,1)的距离与直线y=-1的距离相等的点的轨迹是___________________.3.平面内的点F是定直线l上的一个定点,则到点F和直线l的距离相等的点的轨迹是 ( )
A. 一个点 B.一条线段 C. 一条射线 D.一条直线课堂练习
(1)已知?ABC中,BC长为6,周长为16,那么顶点A在怎样的曲线上运动?
课后练习1.三种圆锥曲线的形成过程.2.椭圆的定义.3.双曲线的定义.4.抛物线的定义.课堂小结
用一个平面去截一个圆锥面,当平面经过圆锥面的顶点时,可得到两条相交直线; 当平面与圆锥面的轴垂直时,截线(平面与圆锥面的交线)是一个圆. 当改变截面与圆锥面的轴的相对位置时,观察截线的变化情况,并思考:
用平面截圆锥面还能得到哪些曲线?这些曲线具有哪些几何特征?
椭圆双曲线抛物线椭圆的定义 平面内到两定点F1 ,F2的距离之和为常数(大于F1 F2距离)的点的轨迹叫椭圆,两个定点叫椭圆的焦点,两焦点的距离叫做椭圆的焦距. 古希腊数学家Dandelin在圆锥截面的两侧分别放置一球,使它们都与截面相切(切点分别为F1,F2),又分别与圆锥面的侧面相切(两球与侧面的公共点分别构成圆O1和圆O2).过M点作圆锥面的一条母线分别交圆O1,圆O2与P,Q两点,因为过球外一点作球的切线长相等,所以
MF1 = MP,MF2 = MQ, MF1 + MF2 =MP + MQ = PQ=定值 F1双曲线的定义 平面内到两个定点F1,F2的距离的差的绝对值等于常数(小于 距离)的点的轨迹叫做双曲线,两个定点F1 , F2叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
平面内与一个定点F和一条定直线l(F不在l上)的距离相等的点的轨迹叫做抛物线.
定点F叫做抛物线的焦点.
定直线l 叫做抛物线的准线. 抛物线定义 椭圆的定义: 可以用数学表达式来体现: 设平面内的动点为M,有
(2a> 的常数)
思考:
在椭圆的定义中,如果这个常数小于或等于 ,动点M的轨迹又如何呢? 平面内到两定点F1,F2的距离和等于常数(大于F1F2)的点的轨迹叫做椭圆,两个定点F1,F2叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.双曲线的定义: 平面内到两定点 F1,F2的距离的差的绝对值等于常数(小于F1F2 )的点的轨迹叫做双曲线,两个定点F1,F2叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.
可以用数学表达式来体现:设平面内的动点为M,有
(0<2a< 的常数)
思考:
在双曲线的定义中,如果这个常数大于或等于 ,动点M的轨迹又如何呢? 抛物线的定义 : 平面内到一个定点F和一条定直线l(F不在l 上)的距离相等的点轨迹叫做抛物线,定点F叫做抛物线的焦点,定直线l叫做抛物线的准线. 设平面内的动点为M ,有MF=d(d为动点M到直线l的距离). 可以用数学表达式来体现:说明: 1.椭圆、双曲线、抛物线统称为圆锥曲线. 2.我们可利用上面的三条关系式来判断动点M的轨迹是什么. 例1,已知三角形ABC中,B(-3,0),C(3,0),且AB,BC,AC成等差数列。
(1)求证:点A在一个椭圆上运动。
(2)写出这个椭圆的焦点坐标。证:(1)根据条件有AB+AC=2BC,
即AB+AC= 12,
即动点A到定点B,C的距离之和为定值12,
且12>6=BC,所以点A在以B,C为焦点的一个椭圆上运动.
(2)B,C即为椭圆的焦点,所以焦点坐标为(-3,0),(3,0)例2 动圆M过定圆C外的一点A,且与圆C外切,问:动圆圆心M的轨迹是什么图形?AMC变题:若动圆M过点A且与圆C 相切呢?例3 已知定点F和定直线l,F不在直线l上,动圆M过F点且与直线l相切,求证:圆心M的轨迹是一条抛物线.分析:欲证明轨迹为抛物线只需抓住抛物线的定义即可. 1.平面内到两定点F1(-4,0)、F2(4,0)的距离和等于10的点的轨迹是 ( )
A. 椭圆 B.双曲线 C. 抛物线 D.线段2.平面内到两定点F1(-1,0)、F2 (1,0)的距离的差的绝对值等于2的点的轨迹是 ( )
A. 椭圆 B.双曲线 C.线段 D.两条射线 课堂练习4.平面内到点F (0,1)的距离与直线y=-1的距离相等的点的轨迹是___________________.3.平面内的点F是定直线l上的一个定点,则到点F和直线l的距离相等的点的轨迹是 ( )
A. 一个点 B.一条线段 C. 一条射线 D.一条直线课堂练习
(1)已知?ABC中,BC长为6,周长为16,那么顶点A在怎样的曲线上运动?
课后练习1.三种圆锥曲线的形成过程.2.椭圆的定义.3.双曲线的定义.4.抛物线的定义.课堂小结
