数学高中苏教版选修(2-1)2.6《曲线与方程》课件
文档属性
| 名称 | 数学高中苏教版选修(2-1)2.6《曲线与方程》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 247.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2013-04-05 00:00:00 | ||
图片预览






文档简介
课件16张PPT。曲线和方程—— 曲线的方程,方程的曲线
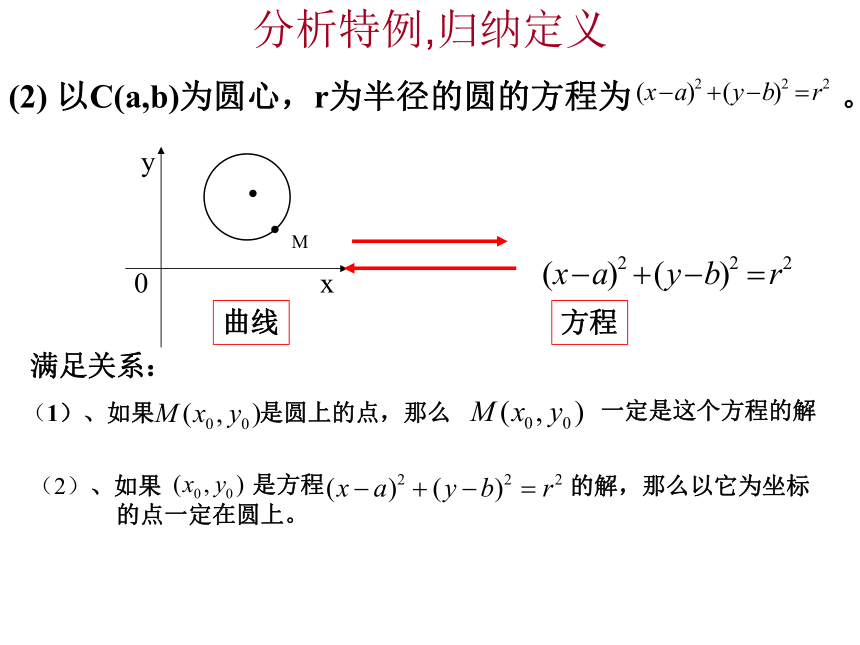
(1)、第一、三象限里两轴间夹角平分线的方程: y=x.y=x第一、三象限角平分线得出关系:曲线方程分析特例,归纳定义满足关系:分析特例,归纳定义(2) 以C(a,b)为圆心,r为半径的圆的方程为 。曲线方程分析特例,归纳定义(3) 椭圆的第二定义椭圆(4)、说明过A(2,0)平行于y轴的直线与方程︱x︱=2的关系①、直线上的点的坐标都满足方程︱x︱=2②、满足方程︱x︱=2的点不一定在直线上结论:过A(2,0)平行于y轴的直线的方程不是︱x︱=2分析特例,归纳定义给定曲线C与二元方程f(x,y)=0,若满足
(1)曲线C上点的坐标(x,y)都是这个方程f(x,y)=0的解;
(2)以方程f(x,y)=0的解为坐标的点都是曲线C上的点.
那么, 方程f(x,y)=0叫做曲线C的方程;
曲线C叫做方程f(x,y)=0的曲线定义分析特例,归纳定义曲线的方程,方程的曲线2、两者间的关系:即:曲线上所有点的集合与此曲线的方程的解集能够一一对应分析特例,归纳定义说明:1.曲线的方程——反映的是图形所满足的数量关系;
方程的曲线——反映的是数量关系所表示的图形.点在曲线上例1:判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴的直线为x=3
(2)到x轴距离为2的点的轨迹方程为y=2
(3)到两坐标轴距离乘积等于1的点的轨迹方程为xy=1对错错学习例题,巩固定义yyy-5y5555555-5-5-5-500xxxx变式训练:写出下列半圆的方程例2:解答下列问题,并说明理由:
(1)判断点A(-4,3),B ,C 是否在方程 所表示的圆上。 课堂练习:下述方程表示的图形分别是下图中的哪一个?例题: 证明以坐标原点为圆心,半径等于5的圆的方程是x2 +y2 = 25。
由1、2可知, x2 +y2 = 25,是以坐标原点为圆心,半径等于5的圆的方程. M1在圆上,M2不在圆上
第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;归纳:
证明已知曲线的方程的方法和步骤 第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.
例4 已知一座圆拱桥的跨度是36m,圆拱
高为6m,以圆拱所对的弦AB为x轴,AB的
垂直平分线为y轴,建立直角坐标系,求圆拱的方程。O1OABxyCP解:设圆心,圆拱上任一点P(x,y),满足,即
即
因为点在圆上,所以
解得
所以圆拱的方程是
例4 (1)方程表示什么曲线?
(2)方程表示什么曲线? (3)判断方程|x|+|y|=1所表示的曲线形状。
(1)、第一、三象限里两轴间夹角平分线的方程: y=x.y=x第一、三象限角平分线得出关系:曲线方程分析特例,归纳定义满足关系:分析特例,归纳定义(2) 以C(a,b)为圆心,r为半径的圆的方程为 。曲线方程分析特例,归纳定义(3) 椭圆的第二定义椭圆(4)、说明过A(2,0)平行于y轴的直线与方程︱x︱=2的关系①、直线上的点的坐标都满足方程︱x︱=2②、满足方程︱x︱=2的点不一定在直线上结论:过A(2,0)平行于y轴的直线的方程不是︱x︱=2分析特例,归纳定义给定曲线C与二元方程f(x,y)=0,若满足
(1)曲线C上点的坐标(x,y)都是这个方程f(x,y)=0的解;
(2)以方程f(x,y)=0的解为坐标的点都是曲线C上的点.
那么, 方程f(x,y)=0叫做曲线C的方程;
曲线C叫做方程f(x,y)=0的曲线定义分析特例,归纳定义曲线的方程,方程的曲线2、两者间的关系:即:曲线上所有点的集合与此曲线的方程的解集能够一一对应分析特例,归纳定义说明:1.曲线的方程——反映的是图形所满足的数量关系;
方程的曲线——反映的是数量关系所表示的图形.点在曲线上例1:判断下列结论的正误并说明理由
(1)过点A(3,0)且垂直于x轴的直线为x=3
(2)到x轴距离为2的点的轨迹方程为y=2
(3)到两坐标轴距离乘积等于1的点的轨迹方程为xy=1对错错学习例题,巩固定义yyy-5y5555555-5-5-5-500xxxx变式训练:写出下列半圆的方程例2:解答下列问题,并说明理由:
(1)判断点A(-4,3),B ,C 是否在方程 所表示的圆上。 课堂练习:下述方程表示的图形分别是下图中的哪一个?例题: 证明以坐标原点为圆心,半径等于5的圆的方程是x2 +y2 = 25。
由1、2可知, x2 +y2 = 25,是以坐标原点为圆心,半径等于5的圆的方程. M1在圆上,M2不在圆上
第一步,设M (x0,y0)是曲线C上任一点,证明(x0,y0)是f(x,y)=0的解;归纳:
证明已知曲线的方程的方法和步骤 第二步,设(x0,y0)是f(x,y)=0的解,证明点M (x0,y0)在曲线C上.
例4 已知一座圆拱桥的跨度是36m,圆拱
高为6m,以圆拱所对的弦AB为x轴,AB的
垂直平分线为y轴,建立直角坐标系,求圆拱的方程。O1OABxyCP解:设圆心,圆拱上任一点P(x,y),满足,即
即
因为点在圆上,所以
解得
所以圆拱的方程是
例4 (1)方程表示什么曲线?
(2)方程表示什么曲线? (3)判断方程|x|+|y|=1所表示的曲线形状。
