4.3.2 公式法--完全平方公式 课件(共27张PPT)
文档属性
| 名称 | 4.3.2 公式法--完全平方公式 课件(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 08:42:26 | ||
图片预览








文档简介
(共27张PPT)
4.3.2公式法
--完全平方公式
北师大版 八年级下
新知导入
1、因式分解:
把一个多项式转化为几个整式的积的形式。
复习回顾:回顾之前所学知识,完成下列问题。
(1)提取公因式法:ma+mb+mc=m(a+b+c)
(2)运用公式法: ① a2-b2=(a+b)(a-b)
2、分解因式学了哪些方法?
新知导入
3、把下列各式分解因式
①ax4-ax2 ② x4-16
解:原式=ax2(x2-1)
=ax2(x+1)(x-1)
解:原式=(x2+4)(x2-4)
=(x2 +4)(x+2)(x-2)
(有公因式,先提公因式)
(因式分解要彻底)
新知导入
1、分解因式x2-25能用平方差公式进行因式分解的多项式有
什么特点?
2、下面的多项式能用平方差公式分解因式吗?
(1) x2+2xy+y2 (2) 9a2-6ab+b2
(1)符号相反的两项 (2)平方差
观察与思考:回答下面两个问题。
新知讲解
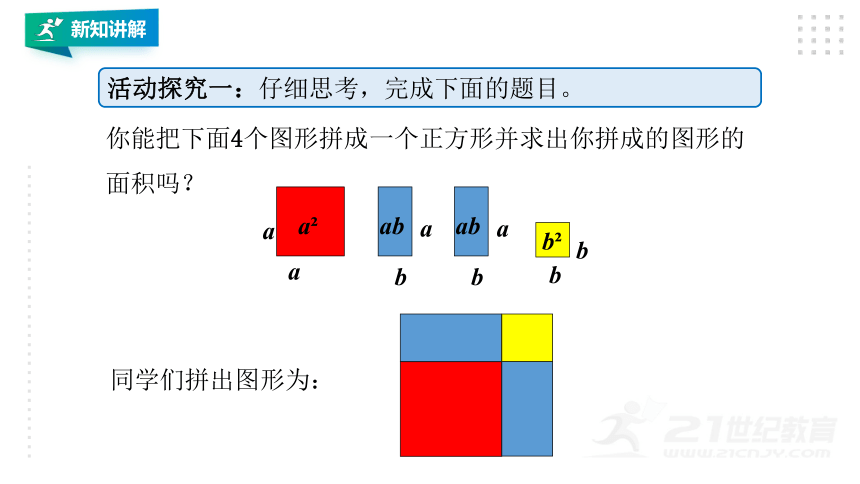
活动探究一:仔细思考,完成下面的题目。
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a
b
ab
新知讲解
这个大正方形的面积可以怎么求?
a2+2ab+b2
(a+b)2
=
a
b
a
b
a
ab
ab
b
(a+b)2
a2+2ab+b2
=
将上面的等式倒过来看,能得到:
a2+2ab+b2
a2-2ab+b2
我们把a +2ab+b 和a -2ab+b 这样的式子叫作完全平方式。
观察这两个式子:
(1)每个多项式有几项?
(3)中间项和第一项,第三项有什么关系?
(2)每个多项式的第一项和第三项有什么特征?
三项
这两项都是数或式的平方,并且符号相同。
是第一项和第三项底数的积的±2倍。
新知讲解
下列各式是不是完全平方式?
(1)a2-4a+4; (2)1+4a ;
(3)4b2+4b-1; (4)a2+ab+b2;
(5)x2+x+0.25.
是
(2)因为它只有两项;
不是
(3)4b 与-1的符号不统一;
不是
分析:
不是
是
(4)因为ab不是a与b的积的2倍.
新知讲解
新知讲解
完全平方式的特点:
1、必须是三项式
2、有两个“项”的平方
3、有这两“项”的2倍或-2倍
完全平方式:
新知讲解
活动探究二:完全平方公式。
新知讲解
a +2ab+ b = (a+b)2
a -2ab+ b = (a-b)2
因式分解
整式乘法
新知讲解
简记口诀:首平方,尾平方,首尾两倍在中央。
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解。
2
a
b
+b2
±
=(a ± b)
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方。
合作探究
x2+14x+49
a +2 a b+b =( a+b)2
解:原式=x2+ 2· x· 7+72 =(x + 7)2
例1:将下列完全平方式因式分解。
注意:正确找出a +2 a b+b =(a+b)2 式子中的a和b。
合作探究
练习1:对照 a ±2ab+b =(a±b) ,完成下面填空。
3.a +4ab+4b =( ) +2· ( ) ·( )+( ) =( )
2.m -6m+9=( ) - 2· ( ) ·( )+( ) =( )
1. x +4x+4= ( ) +2·( )·( )+( ) =( )
x
2
x + 2
a
a 2b
a + 2b
2b
m
m - 3
3
x
2
m
3
合作探究
(m+n)2-6( m+n )+9
解:原式= (m+n)2-2·( m+n )·3+32
=[(m+n)-3] 2
= (m+n-3)2
注意: a +2ab+b =(a+b)2 式子中的a和b既可以是一
个单项式的形式,也可以是一个多项式的形式。
例2:将下列完全平方式因式分解。
合作探究
(a+b)2-12(a+b)+36.
将a+b看成一个整体,设a+b=m,则原式化为m2-12m+36。
解:原式=(a+b)2-2·(a+b) ·6+62
=(a+b-6)2.
练习2:分解因式。
合作探究
(1)3ax2+6axy+3ay2 (2) -x2-4y2+4xy
解:原式=-(x2+4y2-4xy )
=-(x2-4xy+4y2 )
=-[x2-2·x·2y +(2y)2]
= -(x-2y)2
解:原式=3a(x2 +2xy +y2)
= 3a (x+y) 2
注意:注意观察多项式的形式,通过变形提取负号,提负号括号里每一项都要变号。因式分解一定要分解彻底。
例3:把下列各式因式分解
合作探究
(1)-3a2x2+24a2x-48a2;
(2)(a2+4)2-16a2.
=(a2+4+4a)(a2+4-4a)
解:(1)原式=-3a2(x2-8x+16)
=-3a2(x-4)2;
(2)原式=(a2+4)2-(4a)2
=(a+2)2(a-2)2.
有公因式要先提公因式
要检查每一个多项式的因式,看能否继续分解.
练习3:分解因式。
课堂练习
1.下列四个多项式中,能因式分解的是( )
A.a2+1 B.a2-6a+9
C.x2+5y D.x2-5y
2.把多项式4x2y-4xy2-x3分解因式的结果是( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
3.若m=2n+1,则m2-4mn+4n2的值是________。
B
B
1
4.若关于x的多项式x2-8x+m2是完全平方式,则m的值为___________ 。
±4
课堂练习
5.把下列完全平方公式分解因式:
(1)1002-2×100×99+99 (2)342+34×32+162
解:(1)原式=(100-99)
(2)原式=(34+16)2
=1
=2500
课堂练习
6.因式分解
(1)-a3b3+2a2b3-ab3
解:原式=-ab3(a2-2a×1+12)
=-ab3(a-1)2
(2)9 - 12(a-b) + 4 (a-b)2
解:原式=32-2×3×2(a-b)+[2(a-b)] 2
= [3-2(a-b)] 2
=(3-2a+2b)2
课堂练习
7.已知x2+4x+y2-2y+5=0,求 xy 的值。
解:由x2+4x+y2-2y+5=(x2+4x+4)+(y2-2y+1)
=(x+2)2+(y-1)2=0得
x+2=0,y-1=0
∴x=-2,y=1
∴ xy =-2×1=-2
课堂总结
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
一提: ① 对任意多项式分解因式,都必须首先考虑提取公因式。
二套: ② 对于二项式,考虑应用平方差公式分解。 对于三项式,考虑应用完全平方公式 。
三查: ③检查:特别看看多项式因式是否分解彻底。
板书设计
二、分解因式
一提:
二套:
三查:
4.3.2 公式法--完全平方公式
一、公式:
作业布置
1、分解因式
(1)x2+12xy+36y2 (2)32a4+48a2b2+18b4
(3)-2xy-x2-y2 (4)12-36(x-y)+27(x-y)2
https://www.21cnjy.com/help/help_extract.php
4.3.2公式法
--完全平方公式
北师大版 八年级下
新知导入
1、因式分解:
把一个多项式转化为几个整式的积的形式。
复习回顾:回顾之前所学知识,完成下列问题。
(1)提取公因式法:ma+mb+mc=m(a+b+c)
(2)运用公式法: ① a2-b2=(a+b)(a-b)
2、分解因式学了哪些方法?
新知导入
3、把下列各式分解因式
①ax4-ax2 ② x4-16
解:原式=ax2(x2-1)
=ax2(x+1)(x-1)
解:原式=(x2+4)(x2-4)
=(x2 +4)(x+2)(x-2)
(有公因式,先提公因式)
(因式分解要彻底)
新知导入
1、分解因式x2-25能用平方差公式进行因式分解的多项式有
什么特点?
2、下面的多项式能用平方差公式分解因式吗?
(1) x2+2xy+y2 (2) 9a2-6ab+b2
(1)符号相反的两项 (2)平方差
观察与思考:回答下面两个问题。
新知讲解
活动探究一:仔细思考,完成下面的题目。
你能把下面4个图形拼成一个正方形并求出你拼成的图形的面积吗?
同学们拼出图形为:
a
a
b
b
a
b
a
b
ab
a
b
ab
新知讲解
这个大正方形的面积可以怎么求?
a2+2ab+b2
(a+b)2
=
a
b
a
b
a
ab
ab
b
(a+b)2
a2+2ab+b2
=
将上面的等式倒过来看,能得到:
a2+2ab+b2
a2-2ab+b2
我们把a +2ab+b 和a -2ab+b 这样的式子叫作完全平方式。
观察这两个式子:
(1)每个多项式有几项?
(3)中间项和第一项,第三项有什么关系?
(2)每个多项式的第一项和第三项有什么特征?
三项
这两项都是数或式的平方,并且符号相同。
是第一项和第三项底数的积的±2倍。
新知讲解
下列各式是不是完全平方式?
(1)a2-4a+4; (2)1+4a ;
(3)4b2+4b-1; (4)a2+ab+b2;
(5)x2+x+0.25.
是
(2)因为它只有两项;
不是
(3)4b 与-1的符号不统一;
不是
分析:
不是
是
(4)因为ab不是a与b的积的2倍.
新知讲解
新知讲解
完全平方式的特点:
1、必须是三项式
2、有两个“项”的平方
3、有这两“项”的2倍或-2倍
完全平方式:
新知讲解
活动探究二:完全平方公式。
新知讲解
a +2ab+ b = (a+b)2
a -2ab+ b = (a-b)2
因式分解
整式乘法
新知讲解
简记口诀:首平方,尾平方,首尾两倍在中央。
凡具备这些特点的三项式,就是完全平方式,将它写成完全平方形式,便实现了因式分解。
2
a
b
+b2
±
=(a ± b)
a2
首2
+尾2
±2×首×尾
(首±尾)2
两个数的平方和加上(或减去)这两个数的积的2倍,等于这两个数的和(或差)的平方。
合作探究
x2+14x+49
a +2 a b+b =( a+b)2
解:原式=x2+ 2· x· 7+72 =(x + 7)2
例1:将下列完全平方式因式分解。
注意:正确找出a +2 a b+b =(a+b)2 式子中的a和b。
合作探究
练习1:对照 a ±2ab+b =(a±b) ,完成下面填空。
3.a +4ab+4b =( ) +2· ( ) ·( )+( ) =( )
2.m -6m+9=( ) - 2· ( ) ·( )+( ) =( )
1. x +4x+4= ( ) +2·( )·( )+( ) =( )
x
2
x + 2
a
a 2b
a + 2b
2b
m
m - 3
3
x
2
m
3
合作探究
(m+n)2-6( m+n )+9
解:原式= (m+n)2-2·( m+n )·3+32
=[(m+n)-3] 2
= (m+n-3)2
注意: a +2ab+b =(a+b)2 式子中的a和b既可以是一
个单项式的形式,也可以是一个多项式的形式。
例2:将下列完全平方式因式分解。
合作探究
(a+b)2-12(a+b)+36.
将a+b看成一个整体,设a+b=m,则原式化为m2-12m+36。
解:原式=(a+b)2-2·(a+b) ·6+62
=(a+b-6)2.
练习2:分解因式。
合作探究
(1)3ax2+6axy+3ay2 (2) -x2-4y2+4xy
解:原式=-(x2+4y2-4xy )
=-(x2-4xy+4y2 )
=-[x2-2·x·2y +(2y)2]
= -(x-2y)2
解:原式=3a(x2 +2xy +y2)
= 3a (x+y) 2
注意:注意观察多项式的形式,通过变形提取负号,提负号括号里每一项都要变号。因式分解一定要分解彻底。
例3:把下列各式因式分解
合作探究
(1)-3a2x2+24a2x-48a2;
(2)(a2+4)2-16a2.
=(a2+4+4a)(a2+4-4a)
解:(1)原式=-3a2(x2-8x+16)
=-3a2(x-4)2;
(2)原式=(a2+4)2-(4a)2
=(a+2)2(a-2)2.
有公因式要先提公因式
要检查每一个多项式的因式,看能否继续分解.
练习3:分解因式。
课堂练习
1.下列四个多项式中,能因式分解的是( )
A.a2+1 B.a2-6a+9
C.x2+5y D.x2-5y
2.把多项式4x2y-4xy2-x3分解因式的结果是( )
A.4xy(x-y)-x3 B.-x(x-2y)2
C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
3.若m=2n+1,则m2-4mn+4n2的值是________。
B
B
1
4.若关于x的多项式x2-8x+m2是完全平方式,则m的值为___________ 。
±4
课堂练习
5.把下列完全平方公式分解因式:
(1)1002-2×100×99+99 (2)342+34×32+162
解:(1)原式=(100-99)
(2)原式=(34+16)2
=1
=2500
课堂练习
6.因式分解
(1)-a3b3+2a2b3-ab3
解:原式=-ab3(a2-2a×1+12)
=-ab3(a-1)2
(2)9 - 12(a-b) + 4 (a-b)2
解:原式=32-2×3×2(a-b)+[2(a-b)] 2
= [3-2(a-b)] 2
=(3-2a+2b)2
课堂练习
7.已知x2+4x+y2-2y+5=0,求 xy 的值。
解:由x2+4x+y2-2y+5=(x2+4x+4)+(y2-2y+1)
=(x+2)2+(y-1)2=0得
x+2=0,y-1=0
∴x=-2,y=1
∴ xy =-2×1=-2
课堂总结
完全平方公式分解因式
公式
a2±2ab+b2=(a±b)2
特点
一提: ① 对任意多项式分解因式,都必须首先考虑提取公因式。
二套: ② 对于二项式,考虑应用平方差公式分解。 对于三项式,考虑应用完全平方公式 。
三查: ③检查:特别看看多项式因式是否分解彻底。
板书设计
二、分解因式
一提:
二套:
三查:
4.3.2 公式法--完全平方公式
一、公式:
作业布置
1、分解因式
(1)x2+12xy+36y2 (2)32a4+48a2b2+18b4
(3)-2xy-x2-y2 (4)12-36(x-y)+27(x-y)2
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
