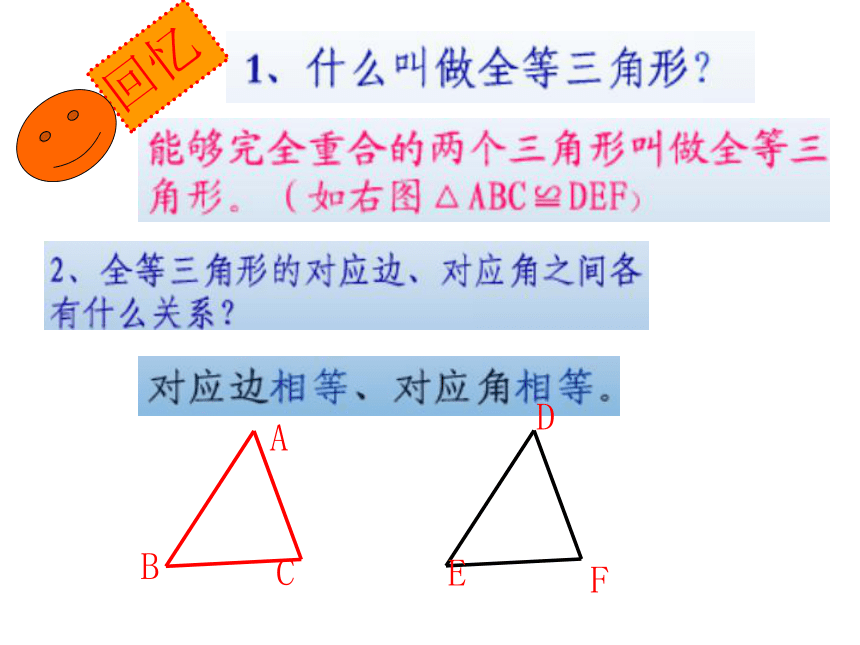
华师版24.3相似三角形定义
图片预览



文档简介
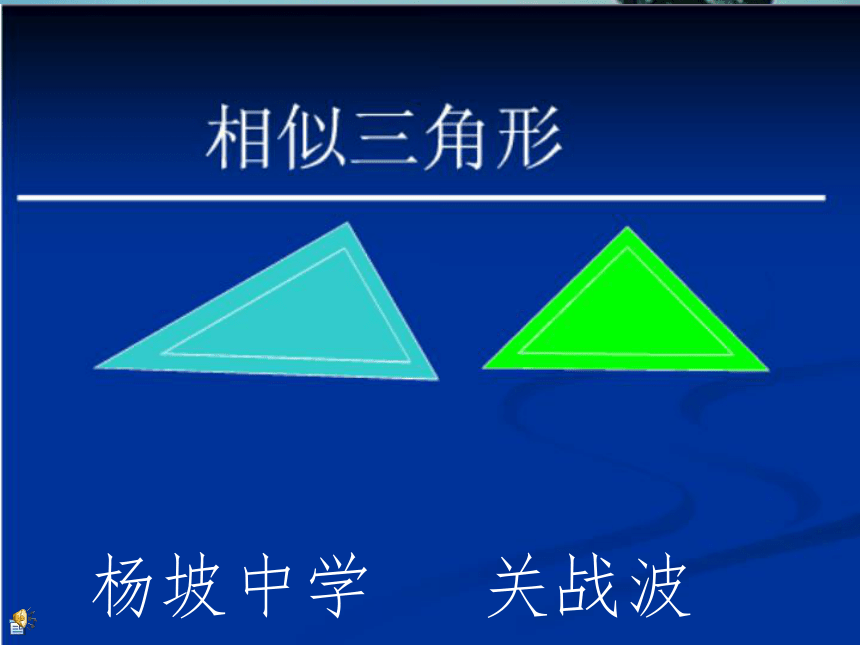
课件17张PPT。杨坡中学 关战波3.相似多边形的性质是什么?对应角相等,对应边成比例.4.如何判断多边形是否是相似图形? 判断对应角是否相等,对应边是否
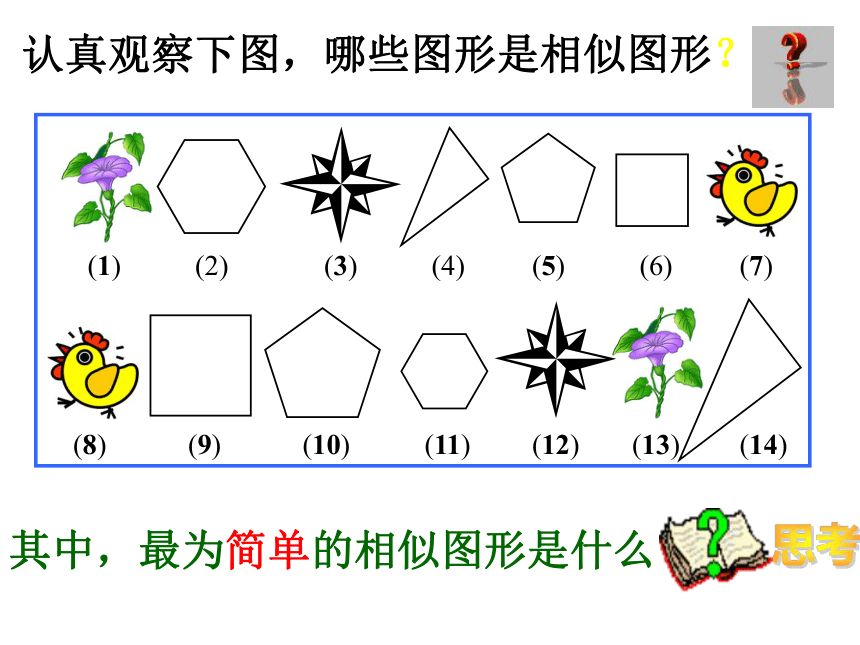
成比例.(两个方面都要同时满足才能够
成立!) 在相似多边形中,最为简单的就
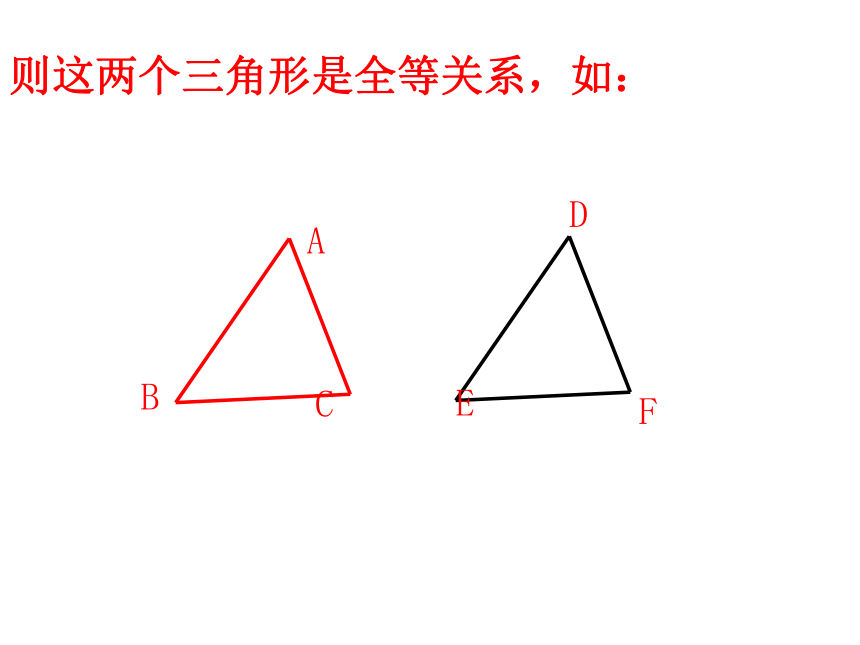
是相似三角形.什么叫相似三角形呢?相似比:注意:相似比具有顺序性噢!当相似比为1是,这两个三角形有什么关系?思考: 则这两个三角形是全等关系,如:∠A = ∠D,∠B =∠E,∠C = ∠F用 “∽”表示: △ABC∽△DEF 注意:要把表示对应角顶点的字母写在对应的位置上!123123如果△ABC与△DEF相似,则找一找已知下图的两个三角形相似,找出图中相似三角形的对应角与对应边,并把它表示出来!对应角:对应边:表示为:△ ABC ∽ △FED∠A = ∠F,∠B =∠E,∠C = ∠DAB→FE,BC→ED,AC→FD归纳总结 1.如果两个多边形相似,那它们具体
有什么性质? 2.如果两个三角形相似,那它们具体
有什么性质?对应角相等,对应边成比例.对应角相等,对应边成比例. 3.相似比(相似系数)的取值范围是
什么?总是正数.想一想 分析:由于DE//BC,所以△ABC与△ADE
的三个角都相等,对应边的比值,通过我们度量和计算也是相等.1、在下面的两组图形中,各有两个相似三角形,试确定x , y , m , n 的值。 例1、如图,已知△ ABC∽ △ADE,AE=50cm,EC=30cm,BC=70cm,∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长。解:(1)因为△ ABC∽ △ADE
所以: ∠AED=∠ACB=40°
在△ADE中,
∠ADE+ ∠AED+ ∠A=180°
即: ∠ADE+ 40° + 45° =180°
所以 ∠ADE=95°例1、如图,已知△ ABC∽ △ADE,AE=50cm,EC=30cm,BC=70cm,∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长。解:(2)因为△ ABC∽ △ADE
所以: 你有什么收获吗?三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形。
△ABC与△DEF相似,就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
性质:相似三角形的各对应角相等,各对应边对应成比例。
如果△ ABC∽ △DEF,那么∠A = ∠D,∠B = ∠E,∠C = ∠F.相似比为1的两个相似三角形是什么样的关系? 这些结论在今后学习的过程中作用很大,要牢记噢!全等三角形欢迎指导 谢谢
成比例.(两个方面都要同时满足才能够
成立!) 在相似多边形中,最为简单的就
是相似三角形.什么叫相似三角形呢?相似比:注意:相似比具有顺序性噢!当相似比为1是,这两个三角形有什么关系?思考: 则这两个三角形是全等关系,如:∠A = ∠D,∠B =∠E,∠C = ∠F用 “∽”表示: △ABC∽△DEF 注意:要把表示对应角顶点的字母写在对应的位置上!123123如果△ABC与△DEF相似,则找一找已知下图的两个三角形相似,找出图中相似三角形的对应角与对应边,并把它表示出来!对应角:对应边:表示为:△ ABC ∽ △FED∠A = ∠F,∠B =∠E,∠C = ∠DAB→FE,BC→ED,AC→FD归纳总结 1.如果两个多边形相似,那它们具体
有什么性质? 2.如果两个三角形相似,那它们具体
有什么性质?对应角相等,对应边成比例.对应角相等,对应边成比例. 3.相似比(相似系数)的取值范围是
什么?总是正数.想一想 分析:由于DE//BC,所以△ABC与△ADE
的三个角都相等,对应边的比值,通过我们度量和计算也是相等.1、在下面的两组图形中,各有两个相似三角形,试确定x , y , m , n 的值。 例1、如图,已知△ ABC∽ △ADE,AE=50cm,EC=30cm,BC=70cm,∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长。解:(1)因为△ ABC∽ △ADE
所以: ∠AED=∠ACB=40°
在△ADE中,
∠ADE+ ∠AED+ ∠A=180°
即: ∠ADE+ 40° + 45° =180°
所以 ∠ADE=95°例1、如图,已知△ ABC∽ △ADE,AE=50cm,EC=30cm,BC=70cm,∠BAC=45°,∠ACB=40°.
(1)求∠AED和∠ADE的大小;
(2)求DE的长。解:(2)因为△ ABC∽ △ADE
所以: 你有什么收获吗?三个角对应相等,三条边对应成比例的两个三角形, 叫做相似三角形。
△ABC与△DEF相似,就记作:△ABC∽△DEF.
注意:要把表示对应角顶点的字母写在对应的位置上!
性质:相似三角形的各对应角相等,各对应边对应成比例。
如果△ ABC∽ △DEF,那么∠A = ∠D,∠B = ∠E,∠C = ∠F.相似比为1的两个相似三角形是什么样的关系? 这些结论在今后学习的过程中作用很大,要牢记噢!全等三角形欢迎指导 谢谢
