有理数节节练
图片预览




文档简介
第一章 有理数
测试1 正数和负数
学习要求
了解正数、负数、有理数的概念,会用正数和负数表示相反意义的量.
课堂学习检测
一、判断题(正确的在括号内画“√”,错误的画“×”)
( )1.某仓库运出30吨货记作-30吨,则运进20吨货记作+20吨.
( )2.节约4吨水与浪费4吨水是一对具有相反意义的量.
( )3.身高增长1.2cm和体重减轻1.2kg是一对具有相反意义的量.
( )4.在小学学过的数前面添上“-”号,得到的就是负数.
二、填空题
5.学校在大桥东面9千米处,那么大桥在学校______面-9千米处.
6.如果以每月生产180个零件为准,超过的零件数记作正数,不足的零件数记作负数,那么1月生产160个零件记作______个,2月生产200个零件记作______个.
7.甲冷库的温度为-6℃,乙冷库的温度比甲冷库低5℃,则乙冷库的温度是______.
8.______既不是正数,也不是负数;它______整数,______有理数(填“是”或“不是”).
9.整数可以看作分母为1的______,有理数包括____________.
10.把下列各数填在相应的大括号内:
正数集合{_______________________________________________________________…}
负数集合{_______________________________________________________________…}
非负数集合{_____________________________________________________________…}
有理数集合{_____________________________________________________________…}
综合、运用、诊断
一、填空题
11.若把公元2008年记作+2008,那么-2008年表示______.
12.潜水艇上浮为正,下潜为负.若潜水艇原先在距水面80米深处,后来两次活动记录的情况是-10米,+20米,则现在潜水艇在距水面______米的深处.
13.是正数而不是整数的有理数是____________________.
14.是整数而不是正数的有理数是____________________.
15.既不是正数,也不是负数的有理数是______________.
16.既不是真分数,也不是零的有理数是______________.
17.在下列数中: 11.11111,95.527,0,+2004,-2?,1.12122122212222,非负有理数有__________________________________________.
二、判断题(正确的在括号里画“√”,错误的画“×”)
( )18.带有正号的数是正数,带有负号的数是负数.
( )19.有理数是正数和小数的统称.
( )20.有最小的正整数,但没有最小的正有理数.
( )21.非负数一定是正数.
( )22.是负分数.
三、解答题
23.-3.782( ).
(A)是负数,不是分数 (B)不是分数,是有理数
(C)是负数,也是分数 (D)是分数,不是有理数
24.下面说法中正确的是( ).
(A)正整数和负整数统称整数 (B)分数不包括整数
(C)正分数,负分数,负整数统称有理数 (D)正整数和正分数统称正有理数
25.一种零件的长度在图纸上是(10±0.05)毫米,表示这种零件的标准尺寸是10毫米,加工要求最大不超过______毫米,最小不小于______毫米.
拓展、探究、思考
26.一批螺帽产品的内径要求可以有±0.02 mm的误差,现抽查5个样品,超过规定的毫米值记为正数,不足值记为负数,检查结果如表.则合乎要求的产品数量为( ).
1
2
3
4
5
+0.031
+0.017
+0.023
-0.021
-0.015
(A)1个 (B)2个 (C)3个 (D)5个
测试2 相反数 数轴
学习要求
掌握一个数的相反数的求法和性质,学习使用数轴,借助数轴理解相反数的几何意义,会借助数轴比较有理数的大小.
课堂学习检测
一、填空题
1.________________的两个数,叫做互为相反数;零的相反数是______.
2.0.4与______互为相反数,______与-(-7)互为相反数,a的相反数是______.
3.规定了______、______和______的______叫数轴.
4.所有的有理数都能用数轴上的______来表示.
5.数轴上,表示-3的点到原点的距离是______个单位长,与原点距离为3个单位长的点表示的数是______。
6.数轴上A,B两点分别在原点的两旁,并且与原点的距离相等,已知点A表示的数是-10,则点B表示的数为______.
二、选择题
7.下面各组数中,互为相反数的有( ).
和 ②-(-6)和+(-6) ③-(-4)和+(+4)
④-(+1)和+(-1) ⑤和+ ⑥和
(A)4组 (B)3组 (C)2组 (D)1组
8.下列说法中正确的有( )
①-3和+3互为相反数;②符号不同的两个数互为相反数;③互为相反数的两个数必定一个是正数,一个是负数;④?的相反数是-3.14;⑤一个数和它的相反数不可能相等.
(A)0个 (B)1个 (C)2个 (D)3个或更多
9.如图,有理数a,b在数轴上对应的点如下,则有( ).
(A)a>0>b (B)a>b>0 (C)a<0<b (D)a<b<0
三、解答题
10.已知一组数:
(1)画一条数轴,并把这些数用数轴上的点表示出来;
(2)把这些数分别填在下面对应的集合中:
负数集合{ …}
正数集合{ …}
(3)请将这些数按从小到大的顺序排列(用“<”连接):______________________.
11.化简下列各数:
(1)______.(2)______.(3)______.
12.比较大小:____________
______.
综合、运用、诊断
一、填空题
13.设a是一个正数,则数轴上表示数a的点在原点______边,与原点的距离是______个单位长度;表示数-a的点在原点______边,与原点的距离是______个单位长度.
14.若-m是正数,则m是______数;m是-m的______数.
15.______的相反数比它本身大,______的相反数等于它本身.
16.大于且小于的整数有______个;比小的非负整数是____________.
17.若p,q两数在数轴上的位置如下图所示,请用“<”或“>”填空.
①p______q; ②-p______0; ③-q______0;
④-p______-q; ⑤-p______q; ⑥p______-q.
18.已知-1<a<0<1<b,请按从小到大的顺序排列-1,-a,0,1,-b为__________.
19.负数的相反数是_______数;把这句话用符号可以表示为_______;
把“若m>0,则-m<0”用文字语言表示为_________________.
二、选择题
20.下列说法中,正确的是( ).
(A)无最大正数,有最大负数 (B)无最小负数,有最小正数
(C)无最小有理数,也无最大有理数 (D)有最小自然数,也有最小整数
21.从原点开始向左移动3个单位,再向右移动1个单位后到达A点,则A点表示的数是 ( ).
(A)3 (B)4 (C)2 (D)-2
三、解答题
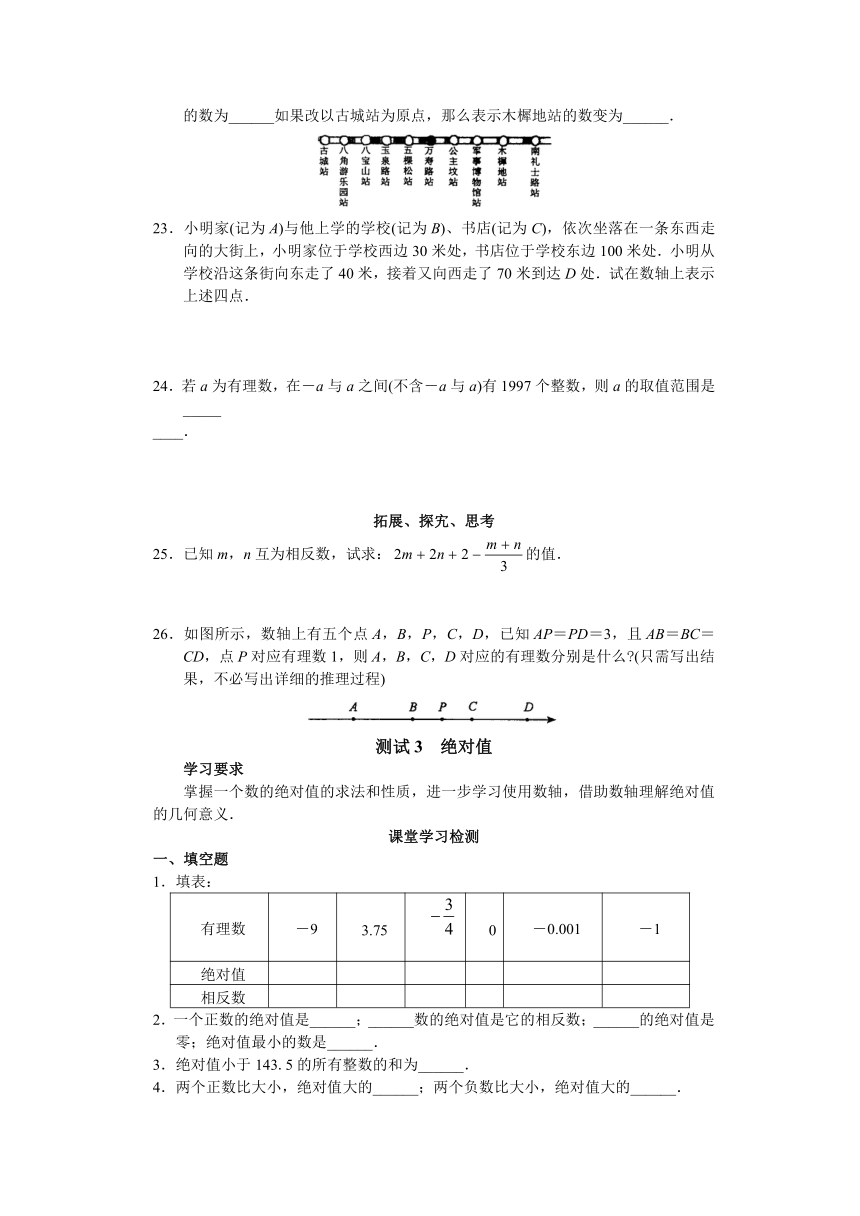
22.如图为北京地铁的部分线路.假设各站之间的距离相等表示为一个单位长.现以万寿路站为原点,向右的方向为正,那么表示木樨地站的数为______表示古城站的数为______如果改以古城站为原点,那么表示木樨地站的数变为______.
23.小明家(记为A)与他上学的学校(记为B)、书店(记为C),依次坐落在一条东西走向的大街上,小明家位于学校西边30米处,书店位于学校东边100米处.小明从学校沿这条街向东走了40米,接着又向西走了70米到达D处.试在数轴上表示上述四点.
24.若a为有理数,在-a与a之间(不含-a与a)有1997个整数,则a的取值范围是_____
____.
拓展、探宄、思考
25.已知m,n互为相反数,试求:的值.
26.如图所示,数轴上有五个点A,B,P,C,D,已知AP=PD=3,且AB=BC=CD,点P对应有理数1,则A,B,C,D对应的有理数分别是什么?(只需写出结果,不必写出详细的推理过程)
测试3 绝对值
学习要求
掌握一个数的绝对值的求法和性质,进一步学习使用数轴,借助数轴理解绝对值的几何意义.
课堂学习检测
一、填空题
1.填表:
有理数
-9
3.75
0
-0.001
-1
绝对值
相反数
2.一个正数的绝对值是______;______数的绝对值是它的相反数;______的绝对值是零;绝对值最小的数是______.
3.绝对值小于143.5的所有整数的和为______.
4.两个正数比大小,绝对值大的______;两个负数比大小,绝对值大的______.
5.绝对值小于4的整数中,最大的整数是______,最小的整数是______.
二、选择题
6.下列各式中,等号不成立的是( ).
(A)|-5|=5 (B)-|5|=-|-5|
(C)|-5|=|5| (D)-|-5|=5
7.的相反数是( ).
(A) (B) (C) (D)
8.下列判断中,错误的是( ).
(A)一个正数的绝对值一定是正数 (B)一个负数的绝对值一定是正数
(C)任何数的绝对值都是正数 (D)任何数的绝对值都不是负数
9.一个数的绝对值是正数,这个数一定是( ).
(A)正数 (B)非零数 (C)任何数 (D)以上都不是
10.在-|-1|,-|0|,,中,负数共有( ).
(A)4个 (B)3个 (C)2个 (D)1个
11.若|a|+a=0,则a是( ).
(A)正数 (B)负数 (C)正数或0 (D)负数或0
三、解答题
12.比大小:________________________,______-1.384,0.0001______-1000,-?______-3.14.
13.计算:
(1)|-16|+|-24|+|+30| (2)
综合、运用、诊断
一、填空题
14.______的相反数小于它本身;______的绝对值大于它本身;______的相反数、绝对值
和它本身都相等.
15.若a>b,a,b均是正数,比较大小:|a|______|b|;
若a<b,a,b均是负数,比较大小:|a|______|b|.
16.若m,n互为相反数,则|m|______|n|.
17.若|x|=|y|,则x,y的关系是______.
18.如果|x|=2,那么x=______;如果|-x|=2,那么x=______.
19.当|a|=a时,则a______.
20.若|a-2|+|b+3|=0,则a=______,b=______.
21.已知|x|=2,|y|=5,且x>y,则x=______,y=______.
22.满足3.5<|x|≤9的x的整数值是______.
23.数a在数轴上的位置如图所示,则|a-2|=______.
二、选择题
24.若a=-1,则-(-|a|)=( ).
(A)1 (B)0 (C)-1 (D)1或-1
25.下列关系一定成立的是( ).
(A)若|m|=|n|,则m=n (B)若|m|=n,则m=n
(C)若|m|=-n,则m=n (D)若m=-n,则|m|=|n|
26.若|x-2|=1,则x=( ).
(A)3 (B)1 (C)-1或1 (D)3或1
27.式子|2x-1|+2取最小值时,x等于( ).
(A)2 (B)-2 (C) (D)
三、解答题
28.飞机提前两分钟到达记为+2,推迟10分钟到达记为-10,准点到达记为0.下面是5家航空公司一年来的到达时间平均值统计表.请利用学过的绝对值的知识评价一下哪家航空公司最好,哪家航空公司最差.
航空公司
A
B
C
D
E
起飞时间
-40
+10
0
-5
+30
29.已知:x,y满足,求7x-3y的值.
拓展、探究、思考
30.若|x|>3,则x的范围是______.
31.若|x|+3=|x-3|,则x的取值范围是______.
32.已知|a|=3,|b|=4,若a,b同号,则|a+b|=______;若a,b异号,则|a+b|=______.据此讨论|a+b|与|a|+|b|的大小关系.
测试4 有理数的加法
学习要求
掌握有理数的加法法则,会使用运算律简算,并能解决简单的实际问题.
课堂学习检测
一、填空题
1.足球比赛中,甲队攻入乙队两球,同时被乙队攻入五球,则计算甲队净胜球数的算式为__________________.
2.-2的相反数与的倒数的和的绝对值等于______.
3.在括号内填入变形的根据:
(a+b)+c=a+(b+c)( )=(b+c)+a( ).
二、选择题
4.下列运算中正确的是( ).
(A)(+8)+(-10)=-(10-8)=-2 (B)(-3)+(-2)=-(3-2)=-1
(C)(-5)+(+6)=+(6+5)=+11 (D)(-6)+(-2)=+(6+2)=+8
5.三个数-15,-5,+10的和,比它们绝对值的和小( ).
(A)-20 (B)20 (C)-40 (D)40
6.如果两个数的和是正数,那么这两个数一定( ).
(A)都是正数 (B)只有一个正数
(C)至少有一个正数 (D)不确定
三、计算题
7.(+8)+(-17)= 8.(-17)+(-15)=
9.(-32.8)+(+51.76)= 10.(-3.07)+(+3.07)=
11. 12.=
13.= 14.
四、解答题
15.某潜水员先潜入水下61米,然后又上升32米,这时潜水员处的位置能否用两种方法表示?
综合、运用、诊断
一、填空题
16.从-56起,逐次加1,得到一串整数:-55,-54,-53…则第100个数为______.
二、选择题
17.两数相加,和比每个加数都小,那么这两个数是( ).
(A)同为负数 (B)两数异号 (C)同为正数 (D)负数和零
18.若m为有理数,则m+|m|的结果必为( ).
(A)正数 (B)负数 (C)非正数 (D)非负数
三、计算题
19.(+7)+(-21)+(-7)+(+21) 20.0+(-3.71)+(+1.71)-(-5)
21. 22.
四、解答题
23.小虫从点O出发在一条直线上来回爬行,向右爬行的路程记为正,向左爬行的路程记为负,爬行的各段路程依次为:+5,-3,+10,-8,-6,+12,-10.(单位:cm)
(1)小虫最后是否回到出发点O?为什么?
(2)小虫离开O点最远时是多少?
(3)在爬行过程中,如果每爬行1cm奖励1粒芝麻,则小虫一共可以得到多少粒芝麻?
拓展、探究、思考
24.有一批食品罐头标准质量为每听454克,现抽取10听样品进行检测,结果如下表:(单位:克)
听号
1
2
3
4
5
质量
444
459
454
459
454
听号
6
7
8
9
10
质量
454
449
454
459
464
这10听罐头的平均质量是多少克?想一想:有没有好的方法算得又快又准确?
25.有理数加法法则:异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,若将正数记为a,负数记为b,将这句话用符号语言表示为_________
_________________________________________________________________________.
26.试比较a+b与a的大小.
测试5 有理数的减法
学习要求
掌握有理数的减法法则和运算技巧,认识减法与加法的内在联系,合理运算.
课堂学习检测
一、填空题
1.若x+m=n,则x=______;若x-m=n,则x=______.
2.计算:(1)(+15)-(-11)=______; (2)(+15)-(+11)=______;
(3)0-(+3.75)=______; (4)|-4|-|-9|=______;
(5)-9-______=0 (6)a-b=a+______.
3.两数之和是11,其中一个加数是14,则另一个加数是______.
4.一个正数与它的绝对值的差是______.
二、选择题
5.室内温度是20℃,室外温度是-1℃,室内温度比室外温度高( ).
(A)19℃ (B)-19℃ (C)21℃ (D)-21℃
6.设a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,则a-b-c的值是( ).
(A)0 (B)-1 (C)2 (D)1
三、判断正误
( )7.两数之差一定小于被减数.
( )8.若两数的差为正数,则两数都为正数.
( )9.零减去一个数仍得这个数.
( )10.一个数减去一个负数,差一定大于被减数.
四、计算题
11. 12.(+12)-(+18)-(+23)+(+51) 13.
14.(+132)-(+124)-(+16)+0+(-132)+(+16) 15.0-(+8)+(-2.7)-(+5)
16. 17.
18.
综合、运用、诊断
一、解答题
19.北京等5个城市的当地时间(单位:时)可在数轴上表示如下:
如果将两地时间的差简称为时差,那么( ).
(A)汉城与纽约的时差为13小时
(B)汉城与多伦多的时差为13小时
(C)北京与纽约的时差为14小时
(D)北京与多伦多的时差为14小时
20.表中列举了国外几个城市与北京的时差(带正号的数表示同一时刻比北京早的时数).如+1表示当北京是上午8:00时,东京是上午9:00.现在是北京时间晚上5点.
城市
时差
巴黎
-7
东京
+1
芝加哥
-14
(1)现在巴黎时间是几点?
(2)小明想给在芝加哥的父亲打电话,现在合适吗?简述你的理由.
21.如图表示某矿井的示意图,以地面为准,A点高度是+4.2米,B,C两点高度分别是-15.6米和-30.5米,A点比B点高多少?比C点呢?
22.一架飞机做特技表演,起飞一段时间后的高度变化如下:(上升记为正数,下降记为负数)+4.5,-3.2,+1.1,0,-1.4.(单位:千米)
(1)请说说“0”的含义.
(2)此时飞机比起飞点高了多少千米?
拓展、探宄、思考
23.求出下列各组数在数轴上对应点之间的距离:
(1)3与-2.2 (2)4.75与2.25
(3)-4与4.5 (4)与
你能发现所得距离与这两个数有什么关系吗?
24.下面的方阵图中,每行、每列、每条对角线上的3个数的和相等.
3
-7
7
5
1
-3
0
-5
9
-1
图① 图② 图③
(1)根据图①中给出的数,对照完成图②;
(2)试着自己找出九个不同的数,完成图③;
(3)想一想图中九个数,最中间的数与其他八个数有什么关系?
测试6 有理数的加减混合运算(一)
学习要求
进一步巩固有理数加法、减法法则和运算,能熟练地将加减混合运算统一成加法运算,理解运算符号和性质符号的意义;运用加法运算律合理简算.
课堂学习检测
一、填空题
1.有理数加减混合运算时,通常先把减法转化为______,然后将正数、负数分别______.
2.4-5-1=-5-1+4的根据是______.
3.计算:(1)(-0.7)-(-0.8)+(-0.9)=______.
(2)______.
(3)-12+11-______+55=0 (4)______与3+(-4)的和为零
二、选择题
4.下列计算错误的是( ).
(A)-2-(-2)=0 (B)-3-4-5=-12
(C)-7-(-3)=-10 (D)12-15=-3
5.如果三个数的和为零,那么这三个数一定是( ).
(A)两个正数,一个负数 (B)两个负数,一个正数
(C)三个都是零 (D)其中两个数之和等于第三个数的相反数
6.若|a-1|+|b+3|=0,则的值是( ),
(A) (B)
(C) (D)
三、计算题
7.-6-6+9 8.-5.4+0.2-0.6+0.8
9. 10.
11. 12.
综合、运用、诊断
一、选择题
13.a,b,c,d在数轴上的对应点位置如图所示,且|a|=|b|,|d|>|c|>|a|,则下列各式中,正确的是( ).
(A)d+c>0 (B)d>c>b>a
(C)a+b=0 (D)b+c>0
14.若a<b,则|b-a+1|-|a-b|等于( ).
(A)4 (B)1 (C)-2a+b+6 (D)不能确定
15.若|a|=4,|b|=3,且a,b异号,则|a-b|等于( ).
(A)7 (B)±1 (C)1 (D)1或7
二、填空题
16.有理数a,b,c在数轴上对应点位置
如图所示,用“>”或“<”填空:
(1)|a|______|b|; (2)a+b+c______0:
(3)a-b+c______0; (4)a+c______b; (5)c-b______a.
三、计算题
17.
18.
19.当a=2.7,b=-3.2,c=-1.8时,求-a-b-c的值.
拓展、探究、思考
20.代数和的规律:
(1)计算1+2-3-4+5+6-7-8+…+2001+2002-2003-2004:
(2)如果在1,2,3…2004这2004个数的前面任意添加正号或负号,再求和,其结果是奇数还是偶数.不好想的话,先从少一点的数列试一试,寻找规律.
测试7 有理数的加减混合运算(二)
学习要求
能熟练地进行有理数加减混合运算,并且会解决简单的实际问题.
课堂学习检测
一、选择题
1.两个有理数的和为负数,那么这两个数一定( ).
(A)都是负数 (B)至少有一个是负数
(C)有一个是0 (D)绝对值不相等
2.已知|x|=3,|y|=2,且x-y=-5,则x+y等于( .
(A)5 (B)-5 (C)1 (D)-1
3.如果a>0,b<0,a+b<0,那么下列各式中大小关系正确的是( ).
(A)-b<-a<b<a (B)-a<b<a<-b
(C)b<-a<-b<a (D)b<-a<a<-b
二、计算题
4. 5.
6. 7.
8. 9.
10.
综合、运用、诊断
11.观察下列两组等式:
根据你的观察,先写出猜想:
(1)( )-( ) (2)( )×( )
然后,用简单方法计算下列各题:
(1) (2)
(3) (4)
12.一个病人每天下午需要测量一次血压,下表为该病人星期一至星期五收缩压的变化情况.若该病人上个星期日的收缩压为160单位.
星期
一
二
三
四
五
收缩压变化
(与前一天相比)
升30单位
降20单位
升17单位
升18单位
降20单位
请算出星期五病人的收缩压值.
拓展、探究、思考
13.若|x|=x,并且|x-3|=3-x,请求出所有符合条件的整数x的值,并计算这些值的和.
14.已知m,n为整数,且|m-2|+|m-n|=1,求m+n的值.
测试8 有理数的乘法
学习要求
会根据有理数的乘法法则进行乘法运算,并运用相关运算律进行简算.
课堂学习检测
一、填空题
1.式子的符号为______.
2.若a=4,b=0,c=-3,d=-5,则c-ad=______,(a-b)(c-d)=______.
二、选择题
3.下列计算正确的是( ).
(A) (B)
(C) (D)
4.两个有理数之积是0,那么这两个有理数( ).
(A)至少有一个是0 (B)都是0 (C)互为倒数 (D)互为相反数
5.这个运算应用了( ).
(A)加法结合律 (B)乘法结合律 (C)乘法交换律 (D)分配律
6.比较a与3a的大小,正确的是( ).
(A)3a>a (B)3a=a
(C)3a<a (D)上述情况都可能
三、计算题
7.直接将答案写在横线上:
(1)______; (2)______;
(3)______; (4)______.
8. 9.
10. 11.
综合、运用、诊断
一、填空题
12.若a<0,b<0,c>0,则(-a)·b·(-c)______0.
13.若a+b<0,且ab>0,则a______0,b______0.
二、选择题
14.已知(-ab)·(-ab)·(-ab)>0,则( ).
(A)ab<0 (B)ab>0 (C)a>0,b<0 (D)a<0,b<0
15.|x-1|+|y+2|+|z-3|=0,则(x-1)(y-2)(z+3)的值为( ).
(A)48 (B)-48 (C)0 (D)xyz
三、计算题
16. 17.
18.
四、解答题
19.巧算下列各题:
(1)
(2)
拓展、探究、思考
20.先观察下图,再解答下题:
小李在街上碰到为救助失学儿童募捐的学生,于是将身上一半的钱捐了出来;接着他又碰到第二个募捐的学生,便又捐出了剩下钱的一半;跟着第三个,第四个,他每次都捐出了剩下钱的一半,身上还剩下一元.请你算一算,最初小李身上有多少元钱?
21.用计算器计算下列各式,将结果写在横线上:
999×21=______; 999×22=______;
999×23=______; 999×24=______.
(1)你发现了什么规律?
(2)不用计算器,你能直接写出999×29的结果吗?
测试9 有理数的除法
学习要求
理解除法与乘法的逆运算关系,会进行有理数除法运算;巩固倒数的概念,能进行简单有理数的加、减、乘、除混合运算.
课堂学习检测
一、填空题
1.若两数之积为1,则这两数互为________;若两数之商为1,则这两数________;若两数之积为-1,则这两数互为________;若两数之商为-1,则这两数互为________.
2.零乘以________都得零,零除以________都得零.
3.若ab>0,b<0,则a________0,且________0;若ab<0,a>0,则b________0,且________0由此可知,ab与的符号________.
一、选择题
4.下列计算正确的是( ).
(A) (B)
(C) (D)
5.已知a的倒数是它本身,则a一定是( ).
(A)0 (B)1 (C)-1 (D)±1
6.一个数与-4的乘积等于,这个数是( ).
(A) (B) (C) (D)
7.填空:(1)=_______; (2)=_______;
(3) _______;(4)=_______;
三、计算题
8. 9.
10.
综合、运用、诊断
一、选择题
11.若xy>0,则(x+y)xy一定( ).
(A)小于0 (B)等于0 (C)大于0 (D)不等于0
12.如果x<y<0,则化简的结果为( ).
(A)0 (B)-2 (C)2 (D)3
二、计算题
13. 14.
15. 16.
三、解答题
17.当a=-2,b=0,c=-5时,求下列式子的值:
(1)a+bc;(2)(a-b)(a+c).
18.在10.5与它的倒数之间有a个整数,在10.5与它的相反数之间有b个整数,求(a+b)÷(a-b)+2的值.
拓展、探究、思考
19.式子的所有可能的值有( ).
(A)2个 (B)3个 (C)4个 (D)无数个
20.如果有理数a,b,c,d都不为0,且它们的积的绝对值等于它们积的相反数,你能确定a,b,c,d中最少有几个是负数,最多有几个是负数吗?
21.一口枯井深64米,井底之蛙想从井底爬上来.第一天白天,它往上爬到井深一半,晚上又滑落了白天所爬路程的一半;第二天白天,它继续往上爬到剩下路程的一半,晚上又滑落了白天所爬路程的一半;每天这样爬,它需要多少天才能爬到井口?做完题后想一想:“一尺之棰,日取其半,万世不竭”这句话的含义.
测试10 有理数的乘方
学习要求
理解有理数乘方的意义,会进行有理数的乘方运算,并体会乘方结果的变化.
课堂学习检测
一、填空题
1.对于(-2)6,6是______的指数,底数是______,(-2)6=______.对-26,6是____的指数,底数是____,-26=______.
2.计算:(1)34=______; (2)-34=______; (3)(-3)4=______;(4)-(-3)4=______;
______; ______; ______;______;
3.当n为正奇数时,(-a)n=______;当n为正偶数时,(-a)n=______.
二、选择题
4.-12的计算结果是( ).
(A)1 (B)-11 (C)-1 (D)-2
5.-0.22的计算结果是( ).
(A)-0.04 (B)0.04 (C)0.4 (D)-0.4
6.的计算结果是( ).
(A) (B) (C) (D)
7.下列各式中,计算结果得0的是( ).
(A)22+(-2)2 (B)-22-22
(C) (D)
8.下列各数互为相反数的是( ).
(A)32与-23 (B)32与(-3)2
(C)32与-32 (D)-32与-(-3)2
三、计算题
9.6×(-2)2÷(-23) 10.
11.(3×2)2+(-2)3×5-(-0.28)÷(-2)2 12.
13. 14.
综合、运用、诊断
一、选择题
15.下列说法中,正确的个数为( ).
①对于任何有理数m,都有m2>0;
②对于任何有理数m,都有m2=(-m)2;
③对于任何有理数m、n(m≠n),都有(m-n)2>0;
④对于任何有理数m,都有m3=(-m)3.
(A)1 (B)2 (C)3 (D)0
16.下列说法中,正确的是( ).
(A)一个数的平方一定大于这个数 (B)一个数的平方一定是正数
(C)一个数的平方一定小于这个数 (D)一个数的平方不可能是负数
二、填空题
17.设n为自然数,则:
(1)(-1)2n-1=______;(2)(-1)2n=______;(3)(-1)n+1=______.
18.当n为正奇数时,(-a)n=______;当n为正偶数时,(-a)n=______.
19.用“>”或“<”填空:
(1)-32________(-2)3; (2)|-3|3________(-3)2;
(3)(-0.2)2________(-0.2)4; (4)________
20.如果-a>a,则a是________;如果|a3|=a3,则a是________.
如果|a2|=-|a2|,则a是________;如果|-a|=-a,则a是________.
三、解答题
21.某种细胞每过30分钟便由1个分裂成2个.请根据你所学知识,描述一下细胞的数量是呈什么方式增长的?并计算5小时后1个细胞可以分裂成多少个细胞.
拓展、探究、思考
22.已知22×83=2n,则n的值为( ).
(A)18 (B)11 (C)8 (D)7
23.根据数表
1
1+3
1+3+5
1+3+5+7
……
可以归纳出一个含有自然数n的等式,你所归纳出的等式是_____________.
24.实验、观察、找规律
计算:31=______;32=______;33=______;34=______;
35=______;36=______;37=______;38=______.
由此推测32004的个位数字是______
测试11 有理数的混合运算(一)
学习要求
掌握有理数混合运算的法则、顺序和运算律,能熟练、合理地进行有理数的加、减、乘、除、乘方的混合的运算.
课堂学习检测
一、填空题
1.混合运算的顺序是先______,再______,后______,______优先.特别要注意的是,如果能运用______时,可改变______达到简化计算的目的.
2.计算含有乘方、乘除、加减三级运算的算式可按加减分段,各段中运算可同时进行:
(先乘方)
(除化乘)
=( )-( )+( )(做乘法)
=( )+( )+( )(减化加)
=______________(用交换律、结合律)
=________(求结果).
3.计算:(1)(-8)-(-4)2×5=_______; (2)[(-8)-(-4)2]×5=_______;
(3)[(-8)-(-4)]2×5=_______; (4)(-8)-(-4×5)2=_______.
4.如果|a|=7,|b|=4,则a+b=_______.
二、计算题(能简算的要简算)
5. 6.
7. 8.(-3)2×(-1.22)÷(-0.3)3 9.(-7.33)×(+42.07)+(-2.07)×(-7.33)
综合、运用、诊断
一、填空题
10.将计算结果直接写在横线上:
(1)-22-(-3)2=_______; (2)________;
(3)-23-3×(-1)3-(-1)4=________; (4)________;
(5)2×(-3)3-4×(-3)+15=________;
(6)-9+12÷(-6)-(-4)2÷(-8)=________;
(7)=________;
(8)________;
(9)________;
二、计算题
11.
12.
13.
三、解答题
14.你能由右图得出计算规律吗?
1+3+5+7+9+11=( )2.
15.用乘方形式表示结果:
(1)(-2)2003+(-2)2004=________; (2)________.
拓展、探究、思考
16.找规律,计算求值.
(1)有一列数:2,4,8,16,x,64…,按规律求x的值,并计算的值.
(2)有一列数:2,7,13,20,x,37…求x的值,并比较(1-x)(1+x)与1-x2的大小.
测试12 有理数的混合运算(二)
学习要求
进一步巩固有理数的混合运算,在运算中使用简单推理,提高运算能力.
课堂学习检测
一、计算题
1.=____________.
2.____________.
3.____________.
4.____________.
二、选择题
5.如果四个有理数的和的是4,其中三个数是-12,-6,9,则第四个数是( ).
(A)-9 (B)15 (C)-18 (D)21
6.如果x=-1,y=3,那么式子的值是( ).
(A) (B)1 (C) (D)
7.已知a,b两数之和、两数之积以及b的相反数都小于0,比较大小正确的是( ).
(A)a-b<a<-b<-a<b-a (B)-a<b<a-b<a<-b<b-a
(C)a-b<-b<-a<a<b-a (D)a-b<a<-b<b<b-a<-a
三、计算题
8. 9.
10. 11.
四、用简便方法计算
12.7+97+997+9997+99997 13.
14. 15.
16.
综合、运用、诊断
一、计算题
17. 18.
二、解答题
19.当(a-2)2+3的值最小时,求a的值及这个最小值.
20.将1~7这七个数字填入图中格内,使每条线上的三个数字之和相等,你能找到几种填法?
拓展、探究、思考
21.已知(a1-1)2+|a2-2|+(a3-3)2+|a4-4|+…+(a2007-2007)2+|a2008-2008|=0,求的值.
测试1 正数和负数
学习要求
了解正数、负数、有理数的概念,会用正数和负数表示相反意义的量.
课堂学习检测
一、判断题(正确的在括号内画“√”,错误的画“×”)
( )1.某仓库运出30吨货记作-30吨,则运进20吨货记作+20吨.
( )2.节约4吨水与浪费4吨水是一对具有相反意义的量.
( )3.身高增长1.2cm和体重减轻1.2kg是一对具有相反意义的量.
( )4.在小学学过的数前面添上“-”号,得到的就是负数.
二、填空题
5.学校在大桥东面9千米处,那么大桥在学校______面-9千米处.
6.如果以每月生产180个零件为准,超过的零件数记作正数,不足的零件数记作负数,那么1月生产160个零件记作______个,2月生产200个零件记作______个.
7.甲冷库的温度为-6℃,乙冷库的温度比甲冷库低5℃,则乙冷库的温度是______.
8.______既不是正数,也不是负数;它______整数,______有理数(填“是”或“不是”).
9.整数可以看作分母为1的______,有理数包括____________.
10.把下列各数填在相应的大括号内:
正数集合{_______________________________________________________________…}
负数集合{_______________________________________________________________…}
非负数集合{_____________________________________________________________…}
有理数集合{_____________________________________________________________…}
综合、运用、诊断
一、填空题
11.若把公元2008年记作+2008,那么-2008年表示______.
12.潜水艇上浮为正,下潜为负.若潜水艇原先在距水面80米深处,后来两次活动记录的情况是-10米,+20米,则现在潜水艇在距水面______米的深处.
13.是正数而不是整数的有理数是____________________.
14.是整数而不是正数的有理数是____________________.
15.既不是正数,也不是负数的有理数是______________.
16.既不是真分数,也不是零的有理数是______________.
17.在下列数中: 11.11111,95.527,0,+2004,-2?,1.12122122212222,非负有理数有__________________________________________.
二、判断题(正确的在括号里画“√”,错误的画“×”)
( )18.带有正号的数是正数,带有负号的数是负数.
( )19.有理数是正数和小数的统称.
( )20.有最小的正整数,但没有最小的正有理数.
( )21.非负数一定是正数.
( )22.是负分数.
三、解答题
23.-3.782( ).
(A)是负数,不是分数 (B)不是分数,是有理数
(C)是负数,也是分数 (D)是分数,不是有理数
24.下面说法中正确的是( ).
(A)正整数和负整数统称整数 (B)分数不包括整数
(C)正分数,负分数,负整数统称有理数 (D)正整数和正分数统称正有理数
25.一种零件的长度在图纸上是(10±0.05)毫米,表示这种零件的标准尺寸是10毫米,加工要求最大不超过______毫米,最小不小于______毫米.
拓展、探究、思考
26.一批螺帽产品的内径要求可以有±0.02 mm的误差,现抽查5个样品,超过规定的毫米值记为正数,不足值记为负数,检查结果如表.则合乎要求的产品数量为( ).
1
2
3
4
5
+0.031
+0.017
+0.023
-0.021
-0.015
(A)1个 (B)2个 (C)3个 (D)5个
测试2 相反数 数轴
学习要求
掌握一个数的相反数的求法和性质,学习使用数轴,借助数轴理解相反数的几何意义,会借助数轴比较有理数的大小.
课堂学习检测
一、填空题
1.________________的两个数,叫做互为相反数;零的相反数是______.
2.0.4与______互为相反数,______与-(-7)互为相反数,a的相反数是______.
3.规定了______、______和______的______叫数轴.
4.所有的有理数都能用数轴上的______来表示.
5.数轴上,表示-3的点到原点的距离是______个单位长,与原点距离为3个单位长的点表示的数是______。
6.数轴上A,B两点分别在原点的两旁,并且与原点的距离相等,已知点A表示的数是-10,则点B表示的数为______.
二、选择题
7.下面各组数中,互为相反数的有( ).
和 ②-(-6)和+(-6) ③-(-4)和+(+4)
④-(+1)和+(-1) ⑤和+ ⑥和
(A)4组 (B)3组 (C)2组 (D)1组
8.下列说法中正确的有( )
①-3和+3互为相反数;②符号不同的两个数互为相反数;③互为相反数的两个数必定一个是正数,一个是负数;④?的相反数是-3.14;⑤一个数和它的相反数不可能相等.
(A)0个 (B)1个 (C)2个 (D)3个或更多
9.如图,有理数a,b在数轴上对应的点如下,则有( ).
(A)a>0>b (B)a>b>0 (C)a<0<b (D)a<b<0
三、解答题
10.已知一组数:
(1)画一条数轴,并把这些数用数轴上的点表示出来;
(2)把这些数分别填在下面对应的集合中:
负数集合{ …}
正数集合{ …}
(3)请将这些数按从小到大的顺序排列(用“<”连接):______________________.
11.化简下列各数:
(1)______.(2)______.(3)______.
12.比较大小:____________
______.
综合、运用、诊断
一、填空题
13.设a是一个正数,则数轴上表示数a的点在原点______边,与原点的距离是______个单位长度;表示数-a的点在原点______边,与原点的距离是______个单位长度.
14.若-m是正数,则m是______数;m是-m的______数.
15.______的相反数比它本身大,______的相反数等于它本身.
16.大于且小于的整数有______个;比小的非负整数是____________.
17.若p,q两数在数轴上的位置如下图所示,请用“<”或“>”填空.
①p______q; ②-p______0; ③-q______0;
④-p______-q; ⑤-p______q; ⑥p______-q.
18.已知-1<a<0<1<b,请按从小到大的顺序排列-1,-a,0,1,-b为__________.
19.负数的相反数是_______数;把这句话用符号可以表示为_______;
把“若m>0,则-m<0”用文字语言表示为_________________.
二、选择题
20.下列说法中,正确的是( ).
(A)无最大正数,有最大负数 (B)无最小负数,有最小正数
(C)无最小有理数,也无最大有理数 (D)有最小自然数,也有最小整数
21.从原点开始向左移动3个单位,再向右移动1个单位后到达A点,则A点表示的数是 ( ).
(A)3 (B)4 (C)2 (D)-2
三、解答题
22.如图为北京地铁的部分线路.假设各站之间的距离相等表示为一个单位长.现以万寿路站为原点,向右的方向为正,那么表示木樨地站的数为______表示古城站的数为______如果改以古城站为原点,那么表示木樨地站的数变为______.
23.小明家(记为A)与他上学的学校(记为B)、书店(记为C),依次坐落在一条东西走向的大街上,小明家位于学校西边30米处,书店位于学校东边100米处.小明从学校沿这条街向东走了40米,接着又向西走了70米到达D处.试在数轴上表示上述四点.
24.若a为有理数,在-a与a之间(不含-a与a)有1997个整数,则a的取值范围是_____
____.
拓展、探宄、思考
25.已知m,n互为相反数,试求:的值.
26.如图所示,数轴上有五个点A,B,P,C,D,已知AP=PD=3,且AB=BC=CD,点P对应有理数1,则A,B,C,D对应的有理数分别是什么?(只需写出结果,不必写出详细的推理过程)
测试3 绝对值
学习要求
掌握一个数的绝对值的求法和性质,进一步学习使用数轴,借助数轴理解绝对值的几何意义.
课堂学习检测
一、填空题
1.填表:
有理数
-9
3.75
0
-0.001
-1
绝对值
相反数
2.一个正数的绝对值是______;______数的绝对值是它的相反数;______的绝对值是零;绝对值最小的数是______.
3.绝对值小于143.5的所有整数的和为______.
4.两个正数比大小,绝对值大的______;两个负数比大小,绝对值大的______.
5.绝对值小于4的整数中,最大的整数是______,最小的整数是______.
二、选择题
6.下列各式中,等号不成立的是( ).
(A)|-5|=5 (B)-|5|=-|-5|
(C)|-5|=|5| (D)-|-5|=5
7.的相反数是( ).
(A) (B) (C) (D)
8.下列判断中,错误的是( ).
(A)一个正数的绝对值一定是正数 (B)一个负数的绝对值一定是正数
(C)任何数的绝对值都是正数 (D)任何数的绝对值都不是负数
9.一个数的绝对值是正数,这个数一定是( ).
(A)正数 (B)非零数 (C)任何数 (D)以上都不是
10.在-|-1|,-|0|,,中,负数共有( ).
(A)4个 (B)3个 (C)2个 (D)1个
11.若|a|+a=0,则a是( ).
(A)正数 (B)负数 (C)正数或0 (D)负数或0
三、解答题
12.比大小:________________________,______-1.384,0.0001______-1000,-?______-3.14.
13.计算:
(1)|-16|+|-24|+|+30| (2)
综合、运用、诊断
一、填空题
14.______的相反数小于它本身;______的绝对值大于它本身;______的相反数、绝对值
和它本身都相等.
15.若a>b,a,b均是正数,比较大小:|a|______|b|;
若a<b,a,b均是负数,比较大小:|a|______|b|.
16.若m,n互为相反数,则|m|______|n|.
17.若|x|=|y|,则x,y的关系是______.
18.如果|x|=2,那么x=______;如果|-x|=2,那么x=______.
19.当|a|=a时,则a______.
20.若|a-2|+|b+3|=0,则a=______,b=______.
21.已知|x|=2,|y|=5,且x>y,则x=______,y=______.
22.满足3.5<|x|≤9的x的整数值是______.
23.数a在数轴上的位置如图所示,则|a-2|=______.
二、选择题
24.若a=-1,则-(-|a|)=( ).
(A)1 (B)0 (C)-1 (D)1或-1
25.下列关系一定成立的是( ).
(A)若|m|=|n|,则m=n (B)若|m|=n,则m=n
(C)若|m|=-n,则m=n (D)若m=-n,则|m|=|n|
26.若|x-2|=1,则x=( ).
(A)3 (B)1 (C)-1或1 (D)3或1
27.式子|2x-1|+2取最小值时,x等于( ).
(A)2 (B)-2 (C) (D)
三、解答题
28.飞机提前两分钟到达记为+2,推迟10分钟到达记为-10,准点到达记为0.下面是5家航空公司一年来的到达时间平均值统计表.请利用学过的绝对值的知识评价一下哪家航空公司最好,哪家航空公司最差.
航空公司
A
B
C
D
E
起飞时间
-40
+10
0
-5
+30
29.已知:x,y满足,求7x-3y的值.
拓展、探究、思考
30.若|x|>3,则x的范围是______.
31.若|x|+3=|x-3|,则x的取值范围是______.
32.已知|a|=3,|b|=4,若a,b同号,则|a+b|=______;若a,b异号,则|a+b|=______.据此讨论|a+b|与|a|+|b|的大小关系.
测试4 有理数的加法
学习要求
掌握有理数的加法法则,会使用运算律简算,并能解决简单的实际问题.
课堂学习检测
一、填空题
1.足球比赛中,甲队攻入乙队两球,同时被乙队攻入五球,则计算甲队净胜球数的算式为__________________.
2.-2的相反数与的倒数的和的绝对值等于______.
3.在括号内填入变形的根据:
(a+b)+c=a+(b+c)( )=(b+c)+a( ).
二、选择题
4.下列运算中正确的是( ).
(A)(+8)+(-10)=-(10-8)=-2 (B)(-3)+(-2)=-(3-2)=-1
(C)(-5)+(+6)=+(6+5)=+11 (D)(-6)+(-2)=+(6+2)=+8
5.三个数-15,-5,+10的和,比它们绝对值的和小( ).
(A)-20 (B)20 (C)-40 (D)40
6.如果两个数的和是正数,那么这两个数一定( ).
(A)都是正数 (B)只有一个正数
(C)至少有一个正数 (D)不确定
三、计算题
7.(+8)+(-17)= 8.(-17)+(-15)=
9.(-32.8)+(+51.76)= 10.(-3.07)+(+3.07)=
11. 12.=
13.= 14.
四、解答题
15.某潜水员先潜入水下61米,然后又上升32米,这时潜水员处的位置能否用两种方法表示?
综合、运用、诊断
一、填空题
16.从-56起,逐次加1,得到一串整数:-55,-54,-53…则第100个数为______.
二、选择题
17.两数相加,和比每个加数都小,那么这两个数是( ).
(A)同为负数 (B)两数异号 (C)同为正数 (D)负数和零
18.若m为有理数,则m+|m|的结果必为( ).
(A)正数 (B)负数 (C)非正数 (D)非负数
三、计算题
19.(+7)+(-21)+(-7)+(+21) 20.0+(-3.71)+(+1.71)-(-5)
21. 22.
四、解答题
23.小虫从点O出发在一条直线上来回爬行,向右爬行的路程记为正,向左爬行的路程记为负,爬行的各段路程依次为:+5,-3,+10,-8,-6,+12,-10.(单位:cm)
(1)小虫最后是否回到出发点O?为什么?
(2)小虫离开O点最远时是多少?
(3)在爬行过程中,如果每爬行1cm奖励1粒芝麻,则小虫一共可以得到多少粒芝麻?
拓展、探究、思考
24.有一批食品罐头标准质量为每听454克,现抽取10听样品进行检测,结果如下表:(单位:克)
听号
1
2
3
4
5
质量
444
459
454
459
454
听号
6
7
8
9
10
质量
454
449
454
459
464
这10听罐头的平均质量是多少克?想一想:有没有好的方法算得又快又准确?
25.有理数加法法则:异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值,若将正数记为a,负数记为b,将这句话用符号语言表示为_________
_________________________________________________________________________.
26.试比较a+b与a的大小.
测试5 有理数的减法
学习要求
掌握有理数的减法法则和运算技巧,认识减法与加法的内在联系,合理运算.
课堂学习检测
一、填空题
1.若x+m=n,则x=______;若x-m=n,则x=______.
2.计算:(1)(+15)-(-11)=______; (2)(+15)-(+11)=______;
(3)0-(+3.75)=______; (4)|-4|-|-9|=______;
(5)-9-______=0 (6)a-b=a+______.
3.两数之和是11,其中一个加数是14,则另一个加数是______.
4.一个正数与它的绝对值的差是______.
二、选择题
5.室内温度是20℃,室外温度是-1℃,室内温度比室外温度高( ).
(A)19℃ (B)-19℃ (C)21℃ (D)-21℃
6.设a是最小的正整数,b是最大的负整数,c是绝对值最小的有理数,则a-b-c的值是( ).
(A)0 (B)-1 (C)2 (D)1
三、判断正误
( )7.两数之差一定小于被减数.
( )8.若两数的差为正数,则两数都为正数.
( )9.零减去一个数仍得这个数.
( )10.一个数减去一个负数,差一定大于被减数.
四、计算题
11. 12.(+12)-(+18)-(+23)+(+51) 13.
14.(+132)-(+124)-(+16)+0+(-132)+(+16) 15.0-(+8)+(-2.7)-(+5)
16. 17.
18.
综合、运用、诊断
一、解答题
19.北京等5个城市的当地时间(单位:时)可在数轴上表示如下:
如果将两地时间的差简称为时差,那么( ).
(A)汉城与纽约的时差为13小时
(B)汉城与多伦多的时差为13小时
(C)北京与纽约的时差为14小时
(D)北京与多伦多的时差为14小时
20.表中列举了国外几个城市与北京的时差(带正号的数表示同一时刻比北京早的时数).如+1表示当北京是上午8:00时,东京是上午9:00.现在是北京时间晚上5点.
城市
时差
巴黎
-7
东京
+1
芝加哥
-14
(1)现在巴黎时间是几点?
(2)小明想给在芝加哥的父亲打电话,现在合适吗?简述你的理由.
21.如图表示某矿井的示意图,以地面为准,A点高度是+4.2米,B,C两点高度分别是-15.6米和-30.5米,A点比B点高多少?比C点呢?
22.一架飞机做特技表演,起飞一段时间后的高度变化如下:(上升记为正数,下降记为负数)+4.5,-3.2,+1.1,0,-1.4.(单位:千米)
(1)请说说“0”的含义.
(2)此时飞机比起飞点高了多少千米?
拓展、探宄、思考
23.求出下列各组数在数轴上对应点之间的距离:
(1)3与-2.2 (2)4.75与2.25
(3)-4与4.5 (4)与
你能发现所得距离与这两个数有什么关系吗?
24.下面的方阵图中,每行、每列、每条对角线上的3个数的和相等.
3
-7
7
5
1
-3
0
-5
9
-1
图① 图② 图③
(1)根据图①中给出的数,对照完成图②;
(2)试着自己找出九个不同的数,完成图③;
(3)想一想图中九个数,最中间的数与其他八个数有什么关系?
测试6 有理数的加减混合运算(一)
学习要求
进一步巩固有理数加法、减法法则和运算,能熟练地将加减混合运算统一成加法运算,理解运算符号和性质符号的意义;运用加法运算律合理简算.
课堂学习检测
一、填空题
1.有理数加减混合运算时,通常先把减法转化为______,然后将正数、负数分别______.
2.4-5-1=-5-1+4的根据是______.
3.计算:(1)(-0.7)-(-0.8)+(-0.9)=______.
(2)______.
(3)-12+11-______+55=0 (4)______与3+(-4)的和为零
二、选择题
4.下列计算错误的是( ).
(A)-2-(-2)=0 (B)-3-4-5=-12
(C)-7-(-3)=-10 (D)12-15=-3
5.如果三个数的和为零,那么这三个数一定是( ).
(A)两个正数,一个负数 (B)两个负数,一个正数
(C)三个都是零 (D)其中两个数之和等于第三个数的相反数
6.若|a-1|+|b+3|=0,则的值是( ),
(A) (B)
(C) (D)
三、计算题
7.-6-6+9 8.-5.4+0.2-0.6+0.8
9. 10.
11. 12.
综合、运用、诊断
一、选择题
13.a,b,c,d在数轴上的对应点位置如图所示,且|a|=|b|,|d|>|c|>|a|,则下列各式中,正确的是( ).
(A)d+c>0 (B)d>c>b>a
(C)a+b=0 (D)b+c>0
14.若a<b,则|b-a+1|-|a-b|等于( ).
(A)4 (B)1 (C)-2a+b+6 (D)不能确定
15.若|a|=4,|b|=3,且a,b异号,则|a-b|等于( ).
(A)7 (B)±1 (C)1 (D)1或7
二、填空题
16.有理数a,b,c在数轴上对应点位置
如图所示,用“>”或“<”填空:
(1)|a|______|b|; (2)a+b+c______0:
(3)a-b+c______0; (4)a+c______b; (5)c-b______a.
三、计算题
17.
18.
19.当a=2.7,b=-3.2,c=-1.8时,求-a-b-c的值.
拓展、探究、思考
20.代数和的规律:
(1)计算1+2-3-4+5+6-7-8+…+2001+2002-2003-2004:
(2)如果在1,2,3…2004这2004个数的前面任意添加正号或负号,再求和,其结果是奇数还是偶数.不好想的话,先从少一点的数列试一试,寻找规律.
测试7 有理数的加减混合运算(二)
学习要求
能熟练地进行有理数加减混合运算,并且会解决简单的实际问题.
课堂学习检测
一、选择题
1.两个有理数的和为负数,那么这两个数一定( ).
(A)都是负数 (B)至少有一个是负数
(C)有一个是0 (D)绝对值不相等
2.已知|x|=3,|y|=2,且x-y=-5,则x+y等于( .
(A)5 (B)-5 (C)1 (D)-1
3.如果a>0,b<0,a+b<0,那么下列各式中大小关系正确的是( ).
(A)-b<-a<b<a (B)-a<b<a<-b
(C)b<-a<-b<a (D)b<-a<a<-b
二、计算题
4. 5.
6. 7.
8. 9.
10.
综合、运用、诊断
11.观察下列两组等式:
根据你的观察,先写出猜想:
(1)( )-( ) (2)( )×( )
然后,用简单方法计算下列各题:
(1) (2)
(3) (4)
12.一个病人每天下午需要测量一次血压,下表为该病人星期一至星期五收缩压的变化情况.若该病人上个星期日的收缩压为160单位.
星期
一
二
三
四
五
收缩压变化
(与前一天相比)
升30单位
降20单位
升17单位
升18单位
降20单位
请算出星期五病人的收缩压值.
拓展、探究、思考
13.若|x|=x,并且|x-3|=3-x,请求出所有符合条件的整数x的值,并计算这些值的和.
14.已知m,n为整数,且|m-2|+|m-n|=1,求m+n的值.
测试8 有理数的乘法
学习要求
会根据有理数的乘法法则进行乘法运算,并运用相关运算律进行简算.
课堂学习检测
一、填空题
1.式子的符号为______.
2.若a=4,b=0,c=-3,d=-5,则c-ad=______,(a-b)(c-d)=______.
二、选择题
3.下列计算正确的是( ).
(A) (B)
(C) (D)
4.两个有理数之积是0,那么这两个有理数( ).
(A)至少有一个是0 (B)都是0 (C)互为倒数 (D)互为相反数
5.这个运算应用了( ).
(A)加法结合律 (B)乘法结合律 (C)乘法交换律 (D)分配律
6.比较a与3a的大小,正确的是( ).
(A)3a>a (B)3a=a
(C)3a<a (D)上述情况都可能
三、计算题
7.直接将答案写在横线上:
(1)______; (2)______;
(3)______; (4)______.
8. 9.
10. 11.
综合、运用、诊断
一、填空题
12.若a<0,b<0,c>0,则(-a)·b·(-c)______0.
13.若a+b<0,且ab>0,则a______0,b______0.
二、选择题
14.已知(-ab)·(-ab)·(-ab)>0,则( ).
(A)ab<0 (B)ab>0 (C)a>0,b<0 (D)a<0,b<0
15.|x-1|+|y+2|+|z-3|=0,则(x-1)(y-2)(z+3)的值为( ).
(A)48 (B)-48 (C)0 (D)xyz
三、计算题
16. 17.
18.
四、解答题
19.巧算下列各题:
(1)
(2)
拓展、探究、思考
20.先观察下图,再解答下题:
小李在街上碰到为救助失学儿童募捐的学生,于是将身上一半的钱捐了出来;接着他又碰到第二个募捐的学生,便又捐出了剩下钱的一半;跟着第三个,第四个,他每次都捐出了剩下钱的一半,身上还剩下一元.请你算一算,最初小李身上有多少元钱?
21.用计算器计算下列各式,将结果写在横线上:
999×21=______; 999×22=______;
999×23=______; 999×24=______.
(1)你发现了什么规律?
(2)不用计算器,你能直接写出999×29的结果吗?
测试9 有理数的除法
学习要求
理解除法与乘法的逆运算关系,会进行有理数除法运算;巩固倒数的概念,能进行简单有理数的加、减、乘、除混合运算.
课堂学习检测
一、填空题
1.若两数之积为1,则这两数互为________;若两数之商为1,则这两数________;若两数之积为-1,则这两数互为________;若两数之商为-1,则这两数互为________.
2.零乘以________都得零,零除以________都得零.
3.若ab>0,b<0,则a________0,且________0;若ab<0,a>0,则b________0,且________0由此可知,ab与的符号________.
一、选择题
4.下列计算正确的是( ).
(A) (B)
(C) (D)
5.已知a的倒数是它本身,则a一定是( ).
(A)0 (B)1 (C)-1 (D)±1
6.一个数与-4的乘积等于,这个数是( ).
(A) (B) (C) (D)
7.填空:(1)=_______; (2)=_______;
(3) _______;(4)=_______;
三、计算题
8. 9.
10.
综合、运用、诊断
一、选择题
11.若xy>0,则(x+y)xy一定( ).
(A)小于0 (B)等于0 (C)大于0 (D)不等于0
12.如果x<y<0,则化简的结果为( ).
(A)0 (B)-2 (C)2 (D)3
二、计算题
13. 14.
15. 16.
三、解答题
17.当a=-2,b=0,c=-5时,求下列式子的值:
(1)a+bc;(2)(a-b)(a+c).
18.在10.5与它的倒数之间有a个整数,在10.5与它的相反数之间有b个整数,求(a+b)÷(a-b)+2的值.
拓展、探究、思考
19.式子的所有可能的值有( ).
(A)2个 (B)3个 (C)4个 (D)无数个
20.如果有理数a,b,c,d都不为0,且它们的积的绝对值等于它们积的相反数,你能确定a,b,c,d中最少有几个是负数,最多有几个是负数吗?
21.一口枯井深64米,井底之蛙想从井底爬上来.第一天白天,它往上爬到井深一半,晚上又滑落了白天所爬路程的一半;第二天白天,它继续往上爬到剩下路程的一半,晚上又滑落了白天所爬路程的一半;每天这样爬,它需要多少天才能爬到井口?做完题后想一想:“一尺之棰,日取其半,万世不竭”这句话的含义.
测试10 有理数的乘方
学习要求
理解有理数乘方的意义,会进行有理数的乘方运算,并体会乘方结果的变化.
课堂学习检测
一、填空题
1.对于(-2)6,6是______的指数,底数是______,(-2)6=______.对-26,6是____的指数,底数是____,-26=______.
2.计算:(1)34=______; (2)-34=______; (3)(-3)4=______;(4)-(-3)4=______;
______; ______; ______;______;
3.当n为正奇数时,(-a)n=______;当n为正偶数时,(-a)n=______.
二、选择题
4.-12的计算结果是( ).
(A)1 (B)-11 (C)-1 (D)-2
5.-0.22的计算结果是( ).
(A)-0.04 (B)0.04 (C)0.4 (D)-0.4
6.的计算结果是( ).
(A) (B) (C) (D)
7.下列各式中,计算结果得0的是( ).
(A)22+(-2)2 (B)-22-22
(C) (D)
8.下列各数互为相反数的是( ).
(A)32与-23 (B)32与(-3)2
(C)32与-32 (D)-32与-(-3)2
三、计算题
9.6×(-2)2÷(-23) 10.
11.(3×2)2+(-2)3×5-(-0.28)÷(-2)2 12.
13. 14.
综合、运用、诊断
一、选择题
15.下列说法中,正确的个数为( ).
①对于任何有理数m,都有m2>0;
②对于任何有理数m,都有m2=(-m)2;
③对于任何有理数m、n(m≠n),都有(m-n)2>0;
④对于任何有理数m,都有m3=(-m)3.
(A)1 (B)2 (C)3 (D)0
16.下列说法中,正确的是( ).
(A)一个数的平方一定大于这个数 (B)一个数的平方一定是正数
(C)一个数的平方一定小于这个数 (D)一个数的平方不可能是负数
二、填空题
17.设n为自然数,则:
(1)(-1)2n-1=______;(2)(-1)2n=______;(3)(-1)n+1=______.
18.当n为正奇数时,(-a)n=______;当n为正偶数时,(-a)n=______.
19.用“>”或“<”填空:
(1)-32________(-2)3; (2)|-3|3________(-3)2;
(3)(-0.2)2________(-0.2)4; (4)________
20.如果-a>a,则a是________;如果|a3|=a3,则a是________.
如果|a2|=-|a2|,则a是________;如果|-a|=-a,则a是________.
三、解答题
21.某种细胞每过30分钟便由1个分裂成2个.请根据你所学知识,描述一下细胞的数量是呈什么方式增长的?并计算5小时后1个细胞可以分裂成多少个细胞.
拓展、探究、思考
22.已知22×83=2n,则n的值为( ).
(A)18 (B)11 (C)8 (D)7
23.根据数表
1
1+3
1+3+5
1+3+5+7
……
可以归纳出一个含有自然数n的等式,你所归纳出的等式是_____________.
24.实验、观察、找规律
计算:31=______;32=______;33=______;34=______;
35=______;36=______;37=______;38=______.
由此推测32004的个位数字是______
测试11 有理数的混合运算(一)
学习要求
掌握有理数混合运算的法则、顺序和运算律,能熟练、合理地进行有理数的加、减、乘、除、乘方的混合的运算.
课堂学习检测
一、填空题
1.混合运算的顺序是先______,再______,后______,______优先.特别要注意的是,如果能运用______时,可改变______达到简化计算的目的.
2.计算含有乘方、乘除、加减三级运算的算式可按加减分段,各段中运算可同时进行:
(先乘方)
(除化乘)
=( )-( )+( )(做乘法)
=( )+( )+( )(减化加)
=______________(用交换律、结合律)
=________(求结果).
3.计算:(1)(-8)-(-4)2×5=_______; (2)[(-8)-(-4)2]×5=_______;
(3)[(-8)-(-4)]2×5=_______; (4)(-8)-(-4×5)2=_______.
4.如果|a|=7,|b|=4,则a+b=_______.
二、计算题(能简算的要简算)
5. 6.
7. 8.(-3)2×(-1.22)÷(-0.3)3 9.(-7.33)×(+42.07)+(-2.07)×(-7.33)
综合、运用、诊断
一、填空题
10.将计算结果直接写在横线上:
(1)-22-(-3)2=_______; (2)________;
(3)-23-3×(-1)3-(-1)4=________; (4)________;
(5)2×(-3)3-4×(-3)+15=________;
(6)-9+12÷(-6)-(-4)2÷(-8)=________;
(7)=________;
(8)________;
(9)________;
二、计算题
11.
12.
13.
三、解答题
14.你能由右图得出计算规律吗?
1+3+5+7+9+11=( )2.
15.用乘方形式表示结果:
(1)(-2)2003+(-2)2004=________; (2)________.
拓展、探究、思考
16.找规律,计算求值.
(1)有一列数:2,4,8,16,x,64…,按规律求x的值,并计算的值.
(2)有一列数:2,7,13,20,x,37…求x的值,并比较(1-x)(1+x)与1-x2的大小.
测试12 有理数的混合运算(二)
学习要求
进一步巩固有理数的混合运算,在运算中使用简单推理,提高运算能力.
课堂学习检测
一、计算题
1.=____________.
2.____________.
3.____________.
4.____________.
二、选择题
5.如果四个有理数的和的是4,其中三个数是-12,-6,9,则第四个数是( ).
(A)-9 (B)15 (C)-18 (D)21
6.如果x=-1,y=3,那么式子的值是( ).
(A) (B)1 (C) (D)
7.已知a,b两数之和、两数之积以及b的相反数都小于0,比较大小正确的是( ).
(A)a-b<a<-b<-a<b-a (B)-a<b<a-b<a<-b<b-a
(C)a-b<-b<-a<a<b-a (D)a-b<a<-b<b<b-a<-a
三、计算题
8. 9.
10. 11.
四、用简便方法计算
12.7+97+997+9997+99997 13.
14. 15.
16.
综合、运用、诊断
一、计算题
17. 18.
二、解答题
19.当(a-2)2+3的值最小时,求a的值及这个最小值.
20.将1~7这七个数字填入图中格内,使每条线上的三个数字之和相等,你能找到几种填法?
拓展、探究、思考
21.已知(a1-1)2+|a2-2|+(a3-3)2+|a4-4|+…+(a2007-2007)2+|a2008-2008|=0,求的值.
