5.2探索轴对称的性质 课件(共29张PPT)
文档属性
| 名称 | 5.2探索轴对称的性质 课件(共29张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 932.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 16:44:28 | ||
图片预览






文档简介
(共29张PPT)
北师大版七年级下册数学
第五章生活中的轴对称
5.2探索轴对称的性质
轴对称图形:如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫作轴对称图形.
这条直线叫这个图形的对称轴.
轴对称:对于两个图形,把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么就说这两个图形成轴对称.
这条直线就是对称轴.
复习引入
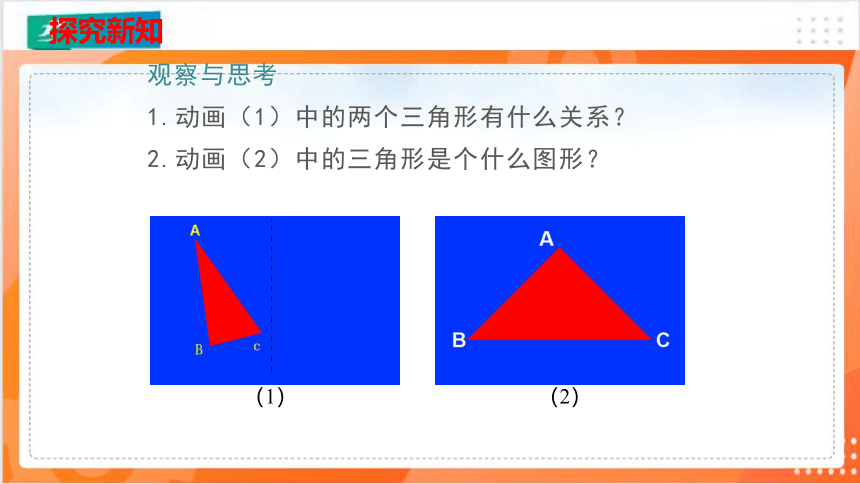
观察与思考
1.动画(1)中的两个三角形有什么关系?
2.动画(2)中的三角形是个什么图形?
(1)
(2)
探究新知
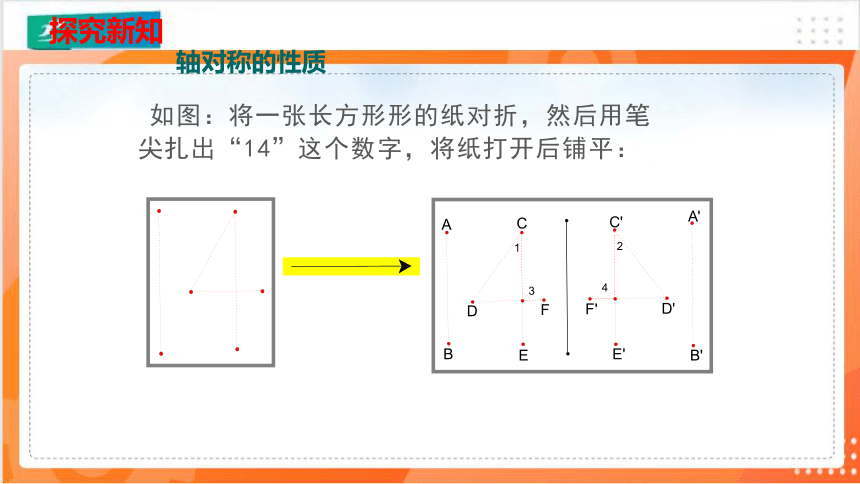
如图:将一张长方形形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平:
轴对称的性质
探究新知
(1)两个“14”有什么关系?
打开
(2)设折痕所在直线为l,连接点E和E′的线段和l
有什么关系?点F和F′呢?
(3)线段AB与A′B′,CD与C′D′有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
与直线l垂直.
AB∥A′B′,CD∥C′D′.
∠1=∠2,∠3=∠4.
成轴对称图形.
探究新知
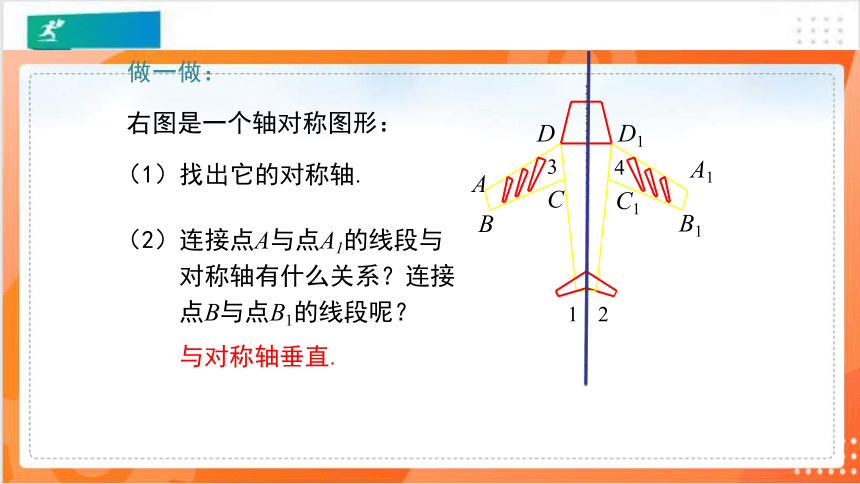
做一做:
右图是一个轴对称图形:
(1)找出它的对称轴.
(2)连接点A与点A1的线段与
对称轴有什么关系?连接
点B与点B1的线段呢?
A
A1
B
C
D
D1
C1
B1
3
4
1
2
与对称轴垂直.
(3)线段AD与线段A1D1有什么
关系?线段BC与B1C1呢?
为什么?
(4)∠1与∠2有什么关系 ∠3
与∠4呢?说说你的理由?
B
C
D
D1
C1
B1
3
4
1
2
思考:综合以上问题,你能得到什么结论?
A
A1
AD=A1D1,BC=B1C1.
∠1=∠2,∠3=∠4.
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
轴对称的性质
总结归纳
随堂练习
1.关于轴对称图形的性质,下列说法不正确的是( )
A.对应点所连的线段与对称轴垂直
B.对应线段相等
C.对应角相等
D.对应线段所在的直线相互平行
D
2.如图,△ABC与△DEF关于直线MN成轴对称,那么线
段AC的对应线段是( )
A. AB
B. DF
C. DE
D. EF
B
3.如图,将长方形纸片ABCD折叠,使点D与点B重合,点
C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和
△BC′F的周长之和为( )
A.3
B.4
C.6
D.8
C
4.如图,△ABC与△A1B1C1关于直线l对称,则∠B
为______.
100°
轴对称图形对称轴的画法
试一试:画出下列图形的对称轴.
如果没有方格子,而又不能折叠,你还能比较准确的画出图形的对称轴吗?
探究新知
做一做
1.画出下面图形的对称轴,画完图后请思考下面的问题:
①能总结你画对称轴的方法吗?
②连结对称点的线段与对称轴有什么关系?
连结对称点的线段被对称轴垂直平分
2.如图,点A和点A’关于某条直线成轴对称,你能画出这条直线吗?
A . . A’
总结归纳
(1)找出图形的任意一组对称点。
画图形的对称轴的画法。
(2)连结对称点。
(3)画出对称点所连线段的垂直平分线,
就可以得到该图形的对称轴。
结论:如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
如图,某同学打台球时想绕过黑球,通过击主球,使主球撞击桌边 MN后反弹来击中彩球.请在图中标明,主球撞在MN上的哪一点才能达到目的 (以主球、彩球的球心A,B来代表两个球)
M
N
主球
彩球
B
A
P
【议一议】
A
B
A′
如图,EFGH是矩形的台球桌面,有两个球分别位于A,B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF,反弹后再击中B球?
E
F
G
H
解:1.作点A关于EF的对称点A′;
2.连接A′B交EF于点C.则沿AC撞击球A,必沿CB反弹击中球B.
C
【试一试】
1
2
3
4
5
6
7
如图:
你能求出这七个角的和吗
【想一想】
1.在一次晚会上,主持人出了一道题目:“如何把
变成一个真正的等式”,很长时间没有人答出,小兰仅仅拿出了一面镜子,就很快解决了这道题目,你知道她是怎样做的吗?
2.成轴对称的图形具有什么样的性质?
对应点所连接的线段被对称轴垂直平分.
3.根据轴对称的性质判断下列每组中图形是否
关于直线l成轴对称?
A
(1)
(2)
A
A
A
A
A
A
O
O
O
A
A
A
A
A
l
l
l
l
l
l
√
√
×
×
×
×
已知对称轴l和一个点A,如
何画出点A关于l的对应点A′
所以点A′就是点A关于l的对称点.
A
A′
作法:
1.过点A作对称轴l的垂线,垂足为B;
2.延长AB 至A′,使得BA′=AB.
B
l
【做一做】
1.如何画线段AB关于直线l
的对称线段A′B′
找关键点作出其对称点,
然后连接线段.
A
B
A′
B′
【练一练】
B′
A′
2.如何画 △ABC关于直线
对称的△ A′B′C′
找关键点作出其对称点,
然后首尾顺次连接线段构成三角形.
A
B
C
C′
1.下列说法错误的是( )
A.等边三角形是轴对称图形
B.轴对称图形的对应边相等,对应角相等
C.成轴对称的两条线段必在对称轴一侧
D.成轴对称的两个图形对应点的连线被对称轴垂直平分
C
课堂练习
2.下面的一些虚线,哪些是图形对称轴,哪些不是图形的对称轴?
②④⑥是图形的对称轴
3.已知,直线 a 与直线 b 是两条相交直线,它是轴对称图形吗?如果是,它有几条对称轴?画图试试看.
a
b
是轴对称图形,有2条对称轴.
4. 画出以下图形的对称轴.
https://www.21cnjy.com/help/help_extract.php
北师大版七年级下册数学
第五章生活中的轴对称
5.2探索轴对称的性质
轴对称图形:如果一个图形沿某条直线对折后,直线两旁的部分能够完全重合,那么这个图形叫作轴对称图形.
这条直线叫这个图形的对称轴.
轴对称:对于两个图形,把一个图形沿着某一条直线对折,如果它能够与另一个图形完全重合,那么就说这两个图形成轴对称.
这条直线就是对称轴.
复习引入
观察与思考
1.动画(1)中的两个三角形有什么关系?
2.动画(2)中的三角形是个什么图形?
(1)
(2)
探究新知
如图:将一张长方形形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平:
轴对称的性质
探究新知
(1)两个“14”有什么关系?
打开
(2)设折痕所在直线为l,连接点E和E′的线段和l
有什么关系?点F和F′呢?
(3)线段AB与A′B′,CD与C′D′有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
与直线l垂直.
AB∥A′B′,CD∥C′D′.
∠1=∠2,∠3=∠4.
成轴对称图形.
探究新知
做一做:
右图是一个轴对称图形:
(1)找出它的对称轴.
(2)连接点A与点A1的线段与
对称轴有什么关系?连接
点B与点B1的线段呢?
A
A1
B
C
D
D1
C1
B1
3
4
1
2
与对称轴垂直.
(3)线段AD与线段A1D1有什么
关系?线段BC与B1C1呢?
为什么?
(4)∠1与∠2有什么关系 ∠3
与∠4呢?说说你的理由?
B
C
D
D1
C1
B1
3
4
1
2
思考:综合以上问题,你能得到什么结论?
A
A1
AD=A1D1,BC=B1C1.
∠1=∠2,∠3=∠4.
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
轴对称的性质
总结归纳
随堂练习
1.关于轴对称图形的性质,下列说法不正确的是( )
A.对应点所连的线段与对称轴垂直
B.对应线段相等
C.对应角相等
D.对应线段所在的直线相互平行
D
2.如图,△ABC与△DEF关于直线MN成轴对称,那么线
段AC的对应线段是( )
A. AB
B. DF
C. DE
D. EF
B
3.如图,将长方形纸片ABCD折叠,使点D与点B重合,点
C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和
△BC′F的周长之和为( )
A.3
B.4
C.6
D.8
C
4.如图,△ABC与△A1B1C1关于直线l对称,则∠B
为______.
100°
轴对称图形对称轴的画法
试一试:画出下列图形的对称轴.
如果没有方格子,而又不能折叠,你还能比较准确的画出图形的对称轴吗?
探究新知
做一做
1.画出下面图形的对称轴,画完图后请思考下面的问题:
①能总结你画对称轴的方法吗?
②连结对称点的线段与对称轴有什么关系?
连结对称点的线段被对称轴垂直平分
2.如图,点A和点A’关于某条直线成轴对称,你能画出这条直线吗?
A . . A’
总结归纳
(1)找出图形的任意一组对称点。
画图形的对称轴的画法。
(2)连结对称点。
(3)画出对称点所连线段的垂直平分线,
就可以得到该图形的对称轴。
结论:如果一个图形是轴对称图形,那么连结对称点的线段的垂直平分线就是该图形的对称轴.
如图,某同学打台球时想绕过黑球,通过击主球,使主球撞击桌边 MN后反弹来击中彩球.请在图中标明,主球撞在MN上的哪一点才能达到目的 (以主球、彩球的球心A,B来代表两个球)
M
N
主球
彩球
B
A
P
【议一议】
A
B
A′
如图,EFGH是矩形的台球桌面,有两个球分别位于A,B两点的位置,试问怎样撞击A球,才能使A球先碰撞台边EF,反弹后再击中B球?
E
F
G
H
解:1.作点A关于EF的对称点A′;
2.连接A′B交EF于点C.则沿AC撞击球A,必沿CB反弹击中球B.
C
【试一试】
1
2
3
4
5
6
7
如图:
你能求出这七个角的和吗
【想一想】
1.在一次晚会上,主持人出了一道题目:“如何把
变成一个真正的等式”,很长时间没有人答出,小兰仅仅拿出了一面镜子,就很快解决了这道题目,你知道她是怎样做的吗?
2.成轴对称的图形具有什么样的性质?
对应点所连接的线段被对称轴垂直平分.
3.根据轴对称的性质判断下列每组中图形是否
关于直线l成轴对称?
A
(1)
(2)
A
A
A
A
A
A
O
O
O
A
A
A
A
A
l
l
l
l
l
l
√
√
×
×
×
×
已知对称轴l和一个点A,如
何画出点A关于l的对应点A′
所以点A′就是点A关于l的对称点.
A
A′
作法:
1.过点A作对称轴l的垂线,垂足为B;
2.延长AB 至A′,使得BA′=AB.
B
l
【做一做】
1.如何画线段AB关于直线l
的对称线段A′B′
找关键点作出其对称点,
然后连接线段.
A
B
A′
B′
【练一练】
B′
A′
2.如何画 △ABC关于直线
对称的△ A′B′C′
找关键点作出其对称点,
然后首尾顺次连接线段构成三角形.
A
B
C
C′
1.下列说法错误的是( )
A.等边三角形是轴对称图形
B.轴对称图形的对应边相等,对应角相等
C.成轴对称的两条线段必在对称轴一侧
D.成轴对称的两个图形对应点的连线被对称轴垂直平分
C
课堂练习
2.下面的一些虚线,哪些是图形对称轴,哪些不是图形的对称轴?
②④⑥是图形的对称轴
3.已知,直线 a 与直线 b 是两条相交直线,它是轴对称图形吗?如果是,它有几条对称轴?画图试试看.
a
b
是轴对称图形,有2条对称轴.
4. 画出以下图形的对称轴.
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
