6.1平行四边形的性质 课件(共40张PPT)
文档属性
| 名称 | 6.1平行四边形的性质 课件(共40张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 16:50:31 | ||
图片预览







文档简介
(共40张PPT)
北师大版八年级下册数学
第六章 平行四边形
6.1 平行四边形的性质
观察下图,平行四边形在生活中无处不在.
情景引入
你还能举出其他的例子吗?
情景引入
活动1:如果将一个三角形的两边分别平移,会得到什么图形?
思考:请观察颜色相同的两组对边,它们有怎样的位置关系呢?
合作探究
一、平行四边形边的相关概念
探究新知
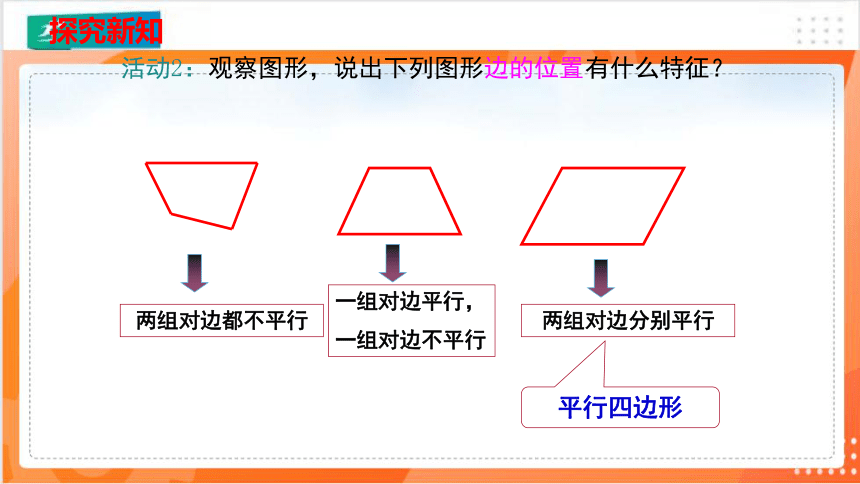
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
平行四边形
活动2:观察图形,说出下列图形边的位置有什么特征?
探究新知
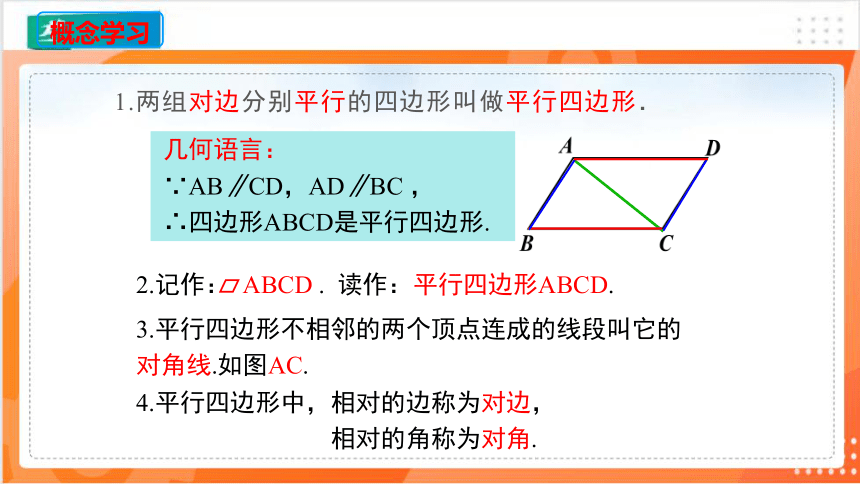
1.两组对边分别平行的四边形叫做平行四边形.
2.记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,
相对的角称为对角.
概念学习
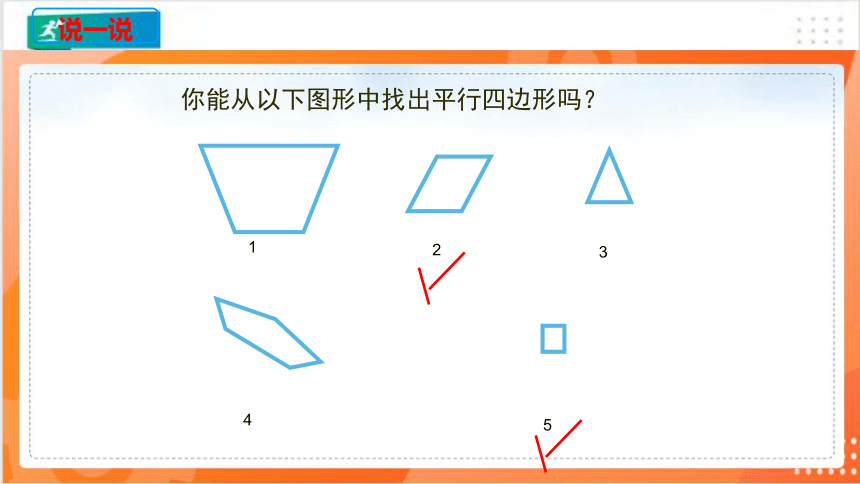
你能从以下图形中找出平行四边形吗?
2
3
1
4
5
说一说
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O 旋转180°,你发现了什么
A
C
D
B
O
合作探究
二、平行四边形边的中心对称性
探究新知
●
A
D
O
C
B
D
B
O
C
A
再看一遍
探究新知
●
A
D
O
C
B
D
B
O
C
A
你有什么猜想?
探究新知
根据刚才的旋转,你知道平行四边形是什么图形?
猜一猜
□ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是 中心对称图形,两条对角线的交点O是它的对称中心.
平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
探究新知
活动3:将两个全等的三角形纸片相等的边重合在一起,你能拼出平行四边形吗?你能拼出几个?与同学交流你的拼法,并把它展示出来.
说一说:通过拼图你可以得到什么启示?
平行四边形对边相等,对角相等.
这个结论正确吗?
三、平行四边形边和角的性质
探究新知
方法1:度量法
A
B
C
D
这个方法准确吗?
平行四边形的一条对角线把平行四边形分成两个全等的三角形;
A
B
C
D
四边形问题
转化
三角形问题
方法2:推理证明
证明:如图,连接AC
∵AD∥BC,AB ∥ CD
∴∠1=∠2,∠3=∠4
又AC是△ABC和△CDA的公共边
∴ △ABC≌ △CDA(ASA)
∴AB=CD,AD=CD
∠B=∠D
已知: ABCD,AB∥CD,AD∥BC.
求证: AB=CD,BC=DA; ∠B=∠D,∠BAD=∠DCB
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.
证明结论
思考:不添加辅助线,你能否直接 运用平行四边形
的定义,证明其对角相等?
A
B
C
D
证明:∵AB∥DC
∠ABC+∠BCD=180°
AD∥BC
∴∠BAD+∠ABC=180°
∴∠BCD=∠BAD
同理 ∠ABC=∠ADC
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质
知识要点
性质定理1
性质定理2
在上一课的“做一做”中,我们还发现:平行
四边形的对角线互相平分. 请你尝试证明这一结论.
四、平行四边形对角线的性质
探究新知
已知:如图, ABCD的两条对角线AC与BD相交于点O.求证:OA=OC, OB=OD.
∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边
相等),
AB∥CD(平行四边形的定义).
∴∠BAO=∠DCO, ∠ABO=∠CDO.
∴△ABO≌△CDO.
∴OA=OC,OB=OD.
你还有其他证明方法吗?与同伴交流.
证明:
例1
例题讲解
定理 平行四边形的对角线互相平分.
总 结
对角线的性质:平行四边形的对角线互相平分.
数学表达式:
如图,∵四边形ABCD是平行四边形,
对角线AC,BD相交于点O,
∴OA=OC,OB=OD.
例2
证明:
∵四边形ABCD是平行四边形,
∴DO=BO(平行四边形的对角线互相平分),
AD∥BC(平行四边形的定义).
∴∠ODE=∠OBF.
∵∠DOE=∠BOF,
∴△DOE≌△BOF. ∴OE=OF.
已知:如图, ABCD的对角线AC与BD相交于点O,
过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF.
例题讲解
已知 ABCD的对角线AC与BD相交于点O,OA,OB,AB他的长分别为3,4,5,求其他各边以及两条对角线的长度.
因为平行四边形的对角线互相平分,
所以AC=2OA=6 ,BD=2OB=8 .
又因为OA2+OB2=32+42=52=AB2,所以AC⊥BD.
由勾股定理,可得AD2=OA2+OD2,
而OD=OB,所以AD2=32+42.
所以AD=5. 同理,可得DC=5,BC=5.
解:
1
针对练习
如图, ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD
B.AO⊥OD
C.AO=OC
D.AO⊥AB
2
C
针对练习
如图, ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10
B.14
C.20
D.22
3
B
针对练习
如图, ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=3,AC=2,BD=4,则AE的长为( )
A.
B.
C.
D.
4
D
针对练习
如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F,若 ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A.14
B.13
C.12
D.10
5
C
针对练习
如图,在 ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,则下列结论:
①CF=AE;
②OE=OF;
③DE=BF;
④图中共有四对全等三角形.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
6
B
针对练习
1.面积公式:平行四边形的面积=底×高(底为平
行四边形的任意一条边,高为这条边与其对边
间的距离);
2.等底等高的平行四边形的面积相等.
五、平行四边形的面积
探究新知
〈福州〉如图,在 ABCD中,DE平分∠ADC,
AD=6,BE=2,则 ABCD的周长是________.
例3
20
求 ABCD的周长,已知一
条边AD=6,只需求出AD的
邻边AB或CD的长即可.
∵四边形ABCD是平行四边形,AD=6,BE=2,
∴AD=BC=6,AD∥BC.
∴EC=BC-BE=6-2=4,∠ADE=∠DEC.
∵DE平分∠ADC,∴∠ADE=∠EDC.
∴∠EDC=∠DEC. ∴DC=EC=4.
∴ ABCD的周长是2×(4+6)=20.
导引:
〈本溪〉如图,在 ABCD中,AB=4,BC=6,
∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24
例4
B
过点A作AE⊥BC于E,根据含30°角的直角三角形
的性质:在直角三角形中,30°角所对的直角边等
于斜边的一半可求出AE的长,利用平行四边形的面
积公式即可求出其面积.
如图,过点A作AE⊥BC于E,
∵在直角三角形ABE中,
∠B=30°,
∴AE= ×AB= ×4=2.
∴平行四边形ABCD的面积=BC·AE=6×2=12.
导引:
求平行四边形的面积时,根据平行四边形的面
积公式,要知道平行四边形的一边长及这边上的高.
平行四边形的高不一定是过顶点的垂线段,因为平
行线间的距离处处相等.
总 结
如图,若 ABCD的周长为36 cm,过点D分别作AB,BC边上的高DE,DF,且DE=4 cm,DF=5 cm, ABCD的面积为( )cm2.
A.40
B.32
C.36
D.50
1
A
如图,过 ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的 AEMG的面积S1与 HCFM的面积S2的大小关系是( )
A.S1>S2
B.S1<S2
C.S1=S2
D.2S1=S2
2
C
如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
3
C
通过本节课的学习,你有什么收获?
1.平行四边形的定义
2.平行四边形的性质
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
课堂小结
3.平行四边形与四边形的关系.
4.学行四边形哪些方面的性质?
5.两条平行线的距离是怎样定义的?有什么性质?
https://www.21cnjy.com/help/help_extract.php
北师大版八年级下册数学
第六章 平行四边形
6.1 平行四边形的性质
观察下图,平行四边形在生活中无处不在.
情景引入
你还能举出其他的例子吗?
情景引入
活动1:如果将一个三角形的两边分别平移,会得到什么图形?
思考:请观察颜色相同的两组对边,它们有怎样的位置关系呢?
合作探究
一、平行四边形边的相关概念
探究新知
两组对边都不平行
一组对边平行,
一组对边不平行
两组对边分别平行
平行四边形
活动2:观察图形,说出下列图形边的位置有什么特征?
探究新知
1.两组对边分别平行的四边形叫做平行四边形.
2.记作: ABCD . 读作:平行四边形ABCD.
几何语言:
∵AB∥CD,AD∥BC ,
∴四边形ABCD是平行四边形.
3.平行四边形不相邻的两个顶点连成的线段叫它的对角线.如图AC.
4.平行四边形中,相对的边称为对边,
相对的角称为对角.
概念学习
你能从以下图形中找出平行四边形吗?
2
3
1
4
5
说一说
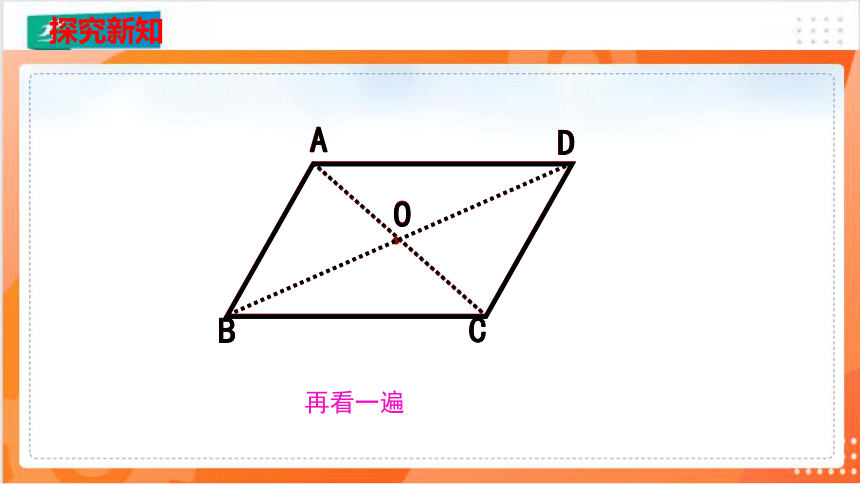
如图,把两张完全相同的平行四边形纸片叠合在一起,在它们的中心O 钉一个图钉,将一个平行四边形绕O 旋转180°,你发现了什么
A
C
D
B
O
合作探究
二、平行四边形边的中心对称性
探究新知
●
A
D
O
C
B
D
B
O
C
A
再看一遍
探究新知
●
A
D
O
C
B
D
B
O
C
A
你有什么猜想?
探究新知
根据刚才的旋转,你知道平行四边形是什么图形?
猜一猜
□ABCD绕它的中心O旋转180°后与自身重合,这时我们说□ABCD是 中心对称图形,两条对角线的交点O是它的对称中心.
平行四边形是中心对称图形,两条对角线的交点是它的对称中心.
探究新知
活动3:将两个全等的三角形纸片相等的边重合在一起,你能拼出平行四边形吗?你能拼出几个?与同学交流你的拼法,并把它展示出来.
说一说:通过拼图你可以得到什么启示?
平行四边形对边相等,对角相等.
这个结论正确吗?
三、平行四边形边和角的性质
探究新知
方法1:度量法
A
B
C
D
这个方法准确吗?
平行四边形的一条对角线把平行四边形分成两个全等的三角形;
A
B
C
D
四边形问题
转化
三角形问题
方法2:推理证明
证明:如图,连接AC
∵AD∥BC,AB ∥ CD
∴∠1=∠2,∠3=∠4
又AC是△ABC和△CDA的公共边
∴ △ABC≌ △CDA(ASA)
∴AB=CD,AD=CD
∠B=∠D
已知: ABCD,AB∥CD,AD∥BC.
求证: AB=CD,BC=DA; ∠B=∠D,∠BAD=∠DCB
又∵∠1=∠2,∠3=∠4
∴∠1+∠4=∠2+∠3
即∠BAD=∠DCB.
证明结论
思考:不添加辅助线,你能否直接 运用平行四边形
的定义,证明其对角相等?
A
B
C
D
证明:∵AB∥DC
∠ABC+∠BCD=180°
AD∥BC
∴∠BAD+∠ABC=180°
∴∠BCD=∠BAD
同理 ∠ABC=∠ADC
几 何 语 言
边
角
文字叙述
对边平行
对边相等
对角相等
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
A
B
C
D
平行四边形的性质
知识要点
性质定理1
性质定理2
在上一课的“做一做”中,我们还发现:平行
四边形的对角线互相平分. 请你尝试证明这一结论.
四、平行四边形对角线的性质
探究新知
已知:如图, ABCD的两条对角线AC与BD相交于点O.求证:OA=OC, OB=OD.
∵四边形ABCD是平行四边形,
∴AB=CD(平行四边形的对边
相等),
AB∥CD(平行四边形的定义).
∴∠BAO=∠DCO, ∠ABO=∠CDO.
∴△ABO≌△CDO.
∴OA=OC,OB=OD.
你还有其他证明方法吗?与同伴交流.
证明:
例1
例题讲解
定理 平行四边形的对角线互相平分.
总 结
对角线的性质:平行四边形的对角线互相平分.
数学表达式:
如图,∵四边形ABCD是平行四边形,
对角线AC,BD相交于点O,
∴OA=OC,OB=OD.
例2
证明:
∵四边形ABCD是平行四边形,
∴DO=BO(平行四边形的对角线互相平分),
AD∥BC(平行四边形的定义).
∴∠ODE=∠OBF.
∵∠DOE=∠BOF,
∴△DOE≌△BOF. ∴OE=OF.
已知:如图, ABCD的对角线AC与BD相交于点O,
过点O的直线与AD,BC分别相交于点E,F.
求证:OE=OF.
例题讲解
已知 ABCD的对角线AC与BD相交于点O,OA,OB,AB他的长分别为3,4,5,求其他各边以及两条对角线的长度.
因为平行四边形的对角线互相平分,
所以AC=2OA=6 ,BD=2OB=8 .
又因为OA2+OB2=32+42=52=AB2,所以AC⊥BD.
由勾股定理,可得AD2=OA2+OD2,
而OD=OB,所以AD2=32+42.
所以AD=5. 同理,可得DC=5,BC=5.
解:
1
针对练习
如图, ABCD的对角线AC,BD相交于点O,则下列说法一定正确的是( )
A.AO=OD
B.AO⊥OD
C.AO=OC
D.AO⊥AB
2
C
针对练习
如图, ABCD的对角线AC,BD相交于点O,且AC+BD=16,CD=6,则△ABO的周长是( )
A.10
B.14
C.20
D.22
3
B
针对练习
如图, ABCD的对角线AC与BD相交于点O,AE⊥BC,垂足为E,AB=3,AC=2,BD=4,则AE的长为( )
A.
B.
C.
D.
4
D
针对练习
如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F,若 ABCD的周长为18,OE=1.5,则四边形EFCD的周长为( )
A.14
B.13
C.12
D.10
5
C
针对练习
如图,在 ABCD中,对角线AC,BD相交于点O,AE⊥BD于点E,CF⊥BD于点F,连接AF,CE,则下列结论:
①CF=AE;
②OE=OF;
③DE=BF;
④图中共有四对全等三角形.
其中正确结论的个数是( )
A.4 B.3 C.2 D.1
6
B
针对练习
1.面积公式:平行四边形的面积=底×高(底为平
行四边形的任意一条边,高为这条边与其对边
间的距离);
2.等底等高的平行四边形的面积相等.
五、平行四边形的面积
探究新知
〈福州〉如图,在 ABCD中,DE平分∠ADC,
AD=6,BE=2,则 ABCD的周长是________.
例3
20
求 ABCD的周长,已知一
条边AD=6,只需求出AD的
邻边AB或CD的长即可.
∵四边形ABCD是平行四边形,AD=6,BE=2,
∴AD=BC=6,AD∥BC.
∴EC=BC-BE=6-2=4,∠ADE=∠DEC.
∵DE平分∠ADC,∴∠ADE=∠EDC.
∴∠EDC=∠DEC. ∴DC=EC=4.
∴ ABCD的周长是2×(4+6)=20.
导引:
〈本溪〉如图,在 ABCD中,AB=4,BC=6,
∠B=30°,则此平行四边形的面积是( )
A.6
B.12
C.18
D.24
例4
B
过点A作AE⊥BC于E,根据含30°角的直角三角形
的性质:在直角三角形中,30°角所对的直角边等
于斜边的一半可求出AE的长,利用平行四边形的面
积公式即可求出其面积.
如图,过点A作AE⊥BC于E,
∵在直角三角形ABE中,
∠B=30°,
∴AE= ×AB= ×4=2.
∴平行四边形ABCD的面积=BC·AE=6×2=12.
导引:
求平行四边形的面积时,根据平行四边形的面
积公式,要知道平行四边形的一边长及这边上的高.
平行四边形的高不一定是过顶点的垂线段,因为平
行线间的距离处处相等.
总 结
如图,若 ABCD的周长为36 cm,过点D分别作AB,BC边上的高DE,DF,且DE=4 cm,DF=5 cm, ABCD的面积为( )cm2.
A.40
B.32
C.36
D.50
1
A
如图,过 ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的 AEMG的面积S1与 HCFM的面积S2的大小关系是( )
A.S1>S2
B.S1<S2
C.S1=S2
D.2S1=S2
2
C
如图,在平行四边形ABCD中,AC,BD为对角线,BC=6,BC边上的高为4,则图中阴影部分的面积为( )
A.3
B.6
C.12
D.24
3
C
通过本节课的学习,你有什么收获?
1.平行四边形的定义
2.平行四边形的性质
平行四边形的对边相等
平行四边形的对角相等
平行四边形的邻角互补
课堂小结
3.平行四边形与四边形的关系.
4.学行四边形哪些方面的性质?
5.两条平行线的距离是怎样定义的?有什么性质?
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
