六年级下学期数学 6.2反比例的意义 课件(19张PPT)
文档属性
| 名称 | 六年级下学期数学 6.2反比例的意义 课件(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 37.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-05-15 15:56:56 | ||
图片预览






文档简介
(共19张PPT)
反比例的意义
预习反馈
一篇文章,编辑设计了以下几种排版方案。
每页字数与页数成反比例吗?为什么?
每页字数与页数成反比例,因为每页字数与页数两种量是相关联的量,它们的积相同,所以成反比例。
财主和帽子的故事
一、反比例的意义
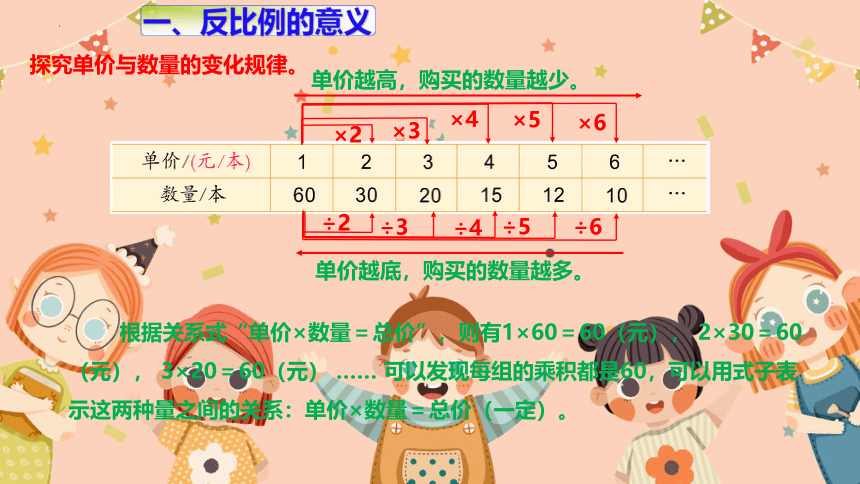
探究单价与数量的变化规律。
×2
÷2
×3
÷3
×4
÷4
×5
×6
÷5
÷6
单价越高,购买的数量越少。
单价越底,购买的数量越多。
根据关系式“单价×数量=总价”,则有1×60=60(元), 2×30=60(元), 3×20=60(元) …… 可以发现每组的乘积都是60,可以用式子表示这两种量之间的关系:单价×数量=总价(一定)。
例1、王叔叔要去游长城,不同的交通工具所需时间如下:
速度/千米
时间/时
10
40
80
12
3
1.5
…
…
观察上表,回答下面的问题:
(1)表中有哪两个量?
(2)时间是怎样随着速度变化的?
(3)相对应的速度和时间有什么变化
规律?
我们可以用下面的式子表示这几个量之间的关系:
单价×数量=总价(一定)
单价和数量是两种相关联的量,单价变化,数量也随着变化。当单价和数量的积总是一定时,笔记本的单价和购买的数量成反比例关系,笔记本的单价和购买的数量是成反比例的量。
讲授新课
1、是两种相关联的量,一种量随着 另一种量变化。
2、变化方向相反,一种量扩大(缩小)
另一种量反而缩小(扩大)。
3、相对应的两个量的乘积是一定的。
如何判断两种量是否成反比例
根据反比例关系的意义,两种量若成反比例关系,必须满足下面这些条件:
⑴两种量相关联。
⑵一种量变化,另一种量也随着变化。
⑶两种量的乘积一定。
(1)表中的两种量是单价和数量;
(2)单价变化,数量也随着变化的;数量越多,单价反而越少;数量越少,单价反而越多。
(3)它们变化的规律是:单价和数量的积总是60。
单价×数量=总价(一定)
试一试:生产240个零件,工作效率和工作时间如下表:
(3)这个乘积表示的实际意义是什么?你能用式子表示它与工作效率、工作时间之间的关系吗?
(4)工作效率和工作时间成反比例吗?为什么?
探究:
课堂探究
这个乘积表示的实际意义是工作总量,
工作效率×工作时间=工作总量,(一定)
工作效率和工作时间成反比例,因为它们的乘积一定。
如果用x和y表示两种相关联的量,用k表示它们的乘积,反比例关系可以表示为:
x×y=k(一定)
讲授新课
运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(3)说明这个积所表示的意义。
这个积表示这批货物的总吨数。
(4)表中相关联的两种量成反比例吗?为什么?
每天运的吨数
需 要 的 天 数
300
6
1
150
2
150
100
75
60
50
3
4
5
每天运的吨数和需要的天数成反比例。
每天运的吨数×需要的天数=货物总吨数(一定)
每天运的吨数和需要的天数成反比例。
因为:每天运的吨数和需要的天数是相关联的量
所以:
分析
随堂检测
下面每个小方格的边长都表示1厘米。看图填表,并回答问题。
(2)长方形的周长一定,长与宽成反比例吗?为什么?
6 4
2 3
5 4
2 3
长方形的周长一定,长与宽不成反比例,因为这两种量是相关联的量,它们的积不相同,所以不成反比例。
看一本180页的书,需用的时间和平均每天看的数量如下表:
时间/天 1 2 3 4 5 6
数量/页 180 90
(1)将表格补充完整。
60
45
36
30
(2)数量和时间成反比吗?为什么?
数量和时间成反比。
因为时间×数量是一定的,数量越多,时间越少。所以成反比。
当堂练习
新知探究
生产240个零件,工作效率和工作时间如下表:
5
6
(3)这个乘积表示的实际意义是什么?你能用式子表示它与工作效率、工作时间之间的关系吗?
工作效率×工作时间=工作总量
(一定)
这个乘积表示这批零件共240个.
做一做
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由.
(1)煤的总量一定,每天的烧煤量和能够烧的天数.
每天的烧煤量和能够烧的天数是两种相关联的量,
每天的烧煤量×能够烧的天数=煤的总量(一定)
每天的烧煤量和能够烧的天数成反比例.
这节课你学到了什么知识?
同学们再见
反比例的意义
预习反馈
一篇文章,编辑设计了以下几种排版方案。
每页字数与页数成反比例吗?为什么?
每页字数与页数成反比例,因为每页字数与页数两种量是相关联的量,它们的积相同,所以成反比例。
财主和帽子的故事
一、反比例的意义
探究单价与数量的变化规律。
×2
÷2
×3
÷3
×4
÷4
×5
×6
÷5
÷6
单价越高,购买的数量越少。
单价越底,购买的数量越多。
根据关系式“单价×数量=总价”,则有1×60=60(元), 2×30=60(元), 3×20=60(元) …… 可以发现每组的乘积都是60,可以用式子表示这两种量之间的关系:单价×数量=总价(一定)。
例1、王叔叔要去游长城,不同的交通工具所需时间如下:
速度/千米
时间/时
10
40
80
12
3
1.5
…
…
观察上表,回答下面的问题:
(1)表中有哪两个量?
(2)时间是怎样随着速度变化的?
(3)相对应的速度和时间有什么变化
规律?
我们可以用下面的式子表示这几个量之间的关系:
单价×数量=总价(一定)
单价和数量是两种相关联的量,单价变化,数量也随着变化。当单价和数量的积总是一定时,笔记本的单价和购买的数量成反比例关系,笔记本的单价和购买的数量是成反比例的量。
讲授新课
1、是两种相关联的量,一种量随着 另一种量变化。
2、变化方向相反,一种量扩大(缩小)
另一种量反而缩小(扩大)。
3、相对应的两个量的乘积是一定的。
如何判断两种量是否成反比例
根据反比例关系的意义,两种量若成反比例关系,必须满足下面这些条件:
⑴两种量相关联。
⑵一种量变化,另一种量也随着变化。
⑶两种量的乘积一定。
(1)表中的两种量是单价和数量;
(2)单价变化,数量也随着变化的;数量越多,单价反而越少;数量越少,单价反而越多。
(3)它们变化的规律是:单价和数量的积总是60。
单价×数量=总价(一定)
试一试:生产240个零件,工作效率和工作时间如下表:
(3)这个乘积表示的实际意义是什么?你能用式子表示它与工作效率、工作时间之间的关系吗?
(4)工作效率和工作时间成反比例吗?为什么?
探究:
课堂探究
这个乘积表示的实际意义是工作总量,
工作效率×工作时间=工作总量,(一定)
工作效率和工作时间成反比例,因为它们的乘积一定。
如果用x和y表示两种相关联的量,用k表示它们的乘积,反比例关系可以表示为:
x×y=k(一定)
讲授新课
运一批货物,每天运的吨数和需要的天数如下表。
根据表回答下面的问题。
(3)说明这个积所表示的意义。
这个积表示这批货物的总吨数。
(4)表中相关联的两种量成反比例吗?为什么?
每天运的吨数
需 要 的 天 数
300
6
1
150
2
150
100
75
60
50
3
4
5
每天运的吨数和需要的天数成反比例。
每天运的吨数×需要的天数=货物总吨数(一定)
每天运的吨数和需要的天数成反比例。
因为:每天运的吨数和需要的天数是相关联的量
所以:
分析
随堂检测
下面每个小方格的边长都表示1厘米。看图填表,并回答问题。
(2)长方形的周长一定,长与宽成反比例吗?为什么?
6 4
2 3
5 4
2 3
长方形的周长一定,长与宽不成反比例,因为这两种量是相关联的量,它们的积不相同,所以不成反比例。
看一本180页的书,需用的时间和平均每天看的数量如下表:
时间/天 1 2 3 4 5 6
数量/页 180 90
(1)将表格补充完整。
60
45
36
30
(2)数量和时间成反比吗?为什么?
数量和时间成反比。
因为时间×数量是一定的,数量越多,时间越少。所以成反比。
当堂练习
新知探究
生产240个零件,工作效率和工作时间如下表:
5
6
(3)这个乘积表示的实际意义是什么?你能用式子表示它与工作效率、工作时间之间的关系吗?
工作效率×工作时间=工作总量
(一定)
这个乘积表示这批零件共240个.
做一做
因为
所以
判断下面每题中的两种量是不是成反比例,并
说明理由.
(1)煤的总量一定,每天的烧煤量和能够烧的天数.
每天的烧煤量和能够烧的天数是两种相关联的量,
每天的烧煤量×能够烧的天数=煤的总量(一定)
每天的烧煤量和能够烧的天数成反比例.
这节课你学到了什么知识?
同学们再见
